一题多解有妙法 深入探究促提升
——2022年高考全国乙卷第23题的探究
林国红
(广东省佛山市乐从中学,广东 佛山 528315)
每年都有不少的优质高考试题,这些试题是命题专家精心设计的杰作,凝聚了命题人的集体智慧,具有权威性、示范性与借鉴性.这当中出现了很多立意深远、思路灵活的题目,值得我们去探究.
1 题目呈现
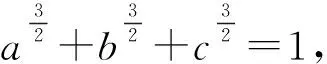
本题是2022年高考全国乙卷文理科的第23题,属于选做题,是一道三元不等式的证明题.题目结构简单,知识方面主要考查不等式的基本性质,不等式的证明等;思想方面主要考查转化与化归、函数等思想.综合考查考生逻辑思维、推理论证等方面的能力,试题的思维过程和证明过程体现了能力立意的命题思想,较好地体现了不等式中的核心内容和基本思想方法的考查.
2 证法探究
2.1 问题(1)的证明
证法1因为a>0,b>0,c>0,则
由三元均值不等式,得


证法2 因为a>0,b>0,c>0,
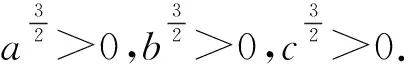
由三元均值不等式,得

证法3因为a>0,b>0,c>0,
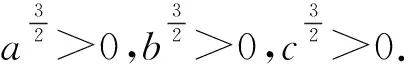
由三元均值不等式,得
由幂平均不等式[1],得



从而证lna+lnb+lnc≤-2ln3.

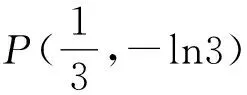
即y=3x-1-ln3.
令g(x)=f(x)-y=lnx-(3x-1-ln3),
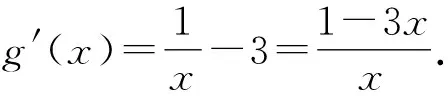




从而g(x)=f(x)-y≤0.
即f(x)=lnx≤y=3x-1-ln3.




从而证lna+lnb+lnc≤-2ln3.


所以f(x)是上凸函数.


2.2 问题(2)的证明









评注①试题的两个问题都可以利用均值不等式证明,均值不等式在证明不等式中应用广泛,也是高中数学的常见方法.②问题(1)的证法4与证法5是通过构造函数来证明不等式,构造函数法是证明不等式的一种重要且巧妙的方法,其关键是通过发掘待证不等式的结构特征,合理变形,构造相应的函数,再通过研究函数的单调性、凹凸性、最值等性质使不等式得以证明,证明过程常用导数作为研究函数性质的工具.
3 试题的命题背景与题根
3.1 试题的命题背景
Nesbitt不等式设x,y,z是正实数,则
①
因为x>0,y>0,z>0,则

②
由不等式②,得



③
由不等式②,得
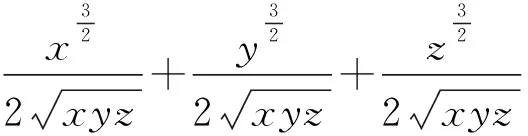

④
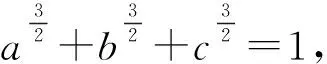
可见,Nesbitt不等式正是2022年高考试题的命题背景.Nesbitt不等式形式优美,内涵极其丰富,由此能演绎出一系列的不等式,可谓花团锦簇、精彩纷呈,因而经典问题也是高考真题的生长点.
3.2 试题的题根
(人教(B版)选修4-5“不等式选讲”第43页第7题)设a,b,c为正实数,求证:
显然,2022年考题的“题根”来源于教材的上述习题(即Nesbitt不等式),只是将习题进行适当的改编.立足教材,选编教材的原题,生成教材的变题,是高考命题的一个不争的事实,这体现了高考命题的公平性和基础性原则.所以教师要善于钻研教材,用“慧眼”去发现有典型性、可拓展性的例习题,善于作解后反思,方法的归类,规律的总结与技巧的揣摩,再进一步对例习题进行挖掘、拓展、引申,扩大其辐射面,以此提高复习的效率.
4 试题的推广


由均值不等式,得

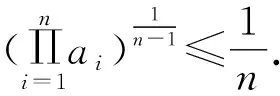

(2)因为ai>0,n≥3,由均值不等式,得
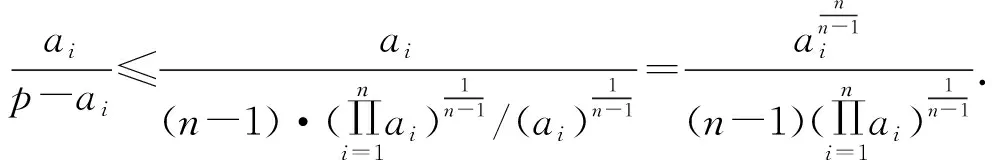

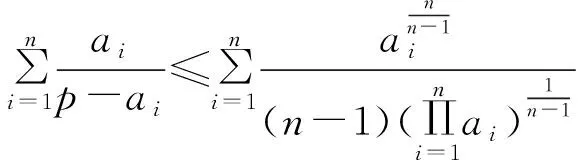

评注显然在推广试题中,当n=3时,就是高考题的情形.
高考试题是精心之作,每年的高考题在命题角度、题型、难度等方面都进行了充分考虑,是知识、能力和思想方法的载体,是命题思想、命题理念的程序化展现,具有典型性、示范性和权威性.高考试题在命制时充分考虑到考生数学能力的个体差异,大多数试题的解答方法、思维方式不是唯一的,给考生提供了较大的发挥空间.这样通过方法的选择、解题时间的长短,甄别出考生能力的差异,达到精确区分考生的目的.也说明高考要突出考查知识主干,贴切教学实际,扎实基础,重视数学的基本能力与思想方法,所以要在平时的学习与训练中重视知识的储备和方法的积累,才有可能缩短思维的长度,达到事半功倍的效果.
高考试题除了具有测试与选拔功能外,还具有良好的教学功能,对中学教学有良好的导向性,要了解高考动向、把握高考脉搏,高考试题的研究分析是重要的路径.因此要充分认识高考题所蕴含的价值,对典型高考题要深入挖掘,探求试题背后的思想方法,并注重一题多解,力求对所学的知识融会贯通,从而实现高考题的教学功能的最大化、最优化.

