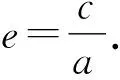对一道椭圆试题的深入探究
董 强
(西安市第八十五中学,陕西 西安 710061)
笔者在给高二学生的复习试题中有一道有关椭圆中证明直线斜率为定值的问题[1],通过课堂和学生的互动探究,发现这是一道蕴含椭圆本质属性的试题,可以进行推广.试题解答过程中所呈现的解析思路和具体方法对圆锥曲线问题有着积极的意义,体现了思考圆锥曲线问题的一般规律和基本方向.
1 试题呈现

(1)求椭圆C的方程;
(2)过点F2作垂直于x轴的直线l交椭圆于A,B两点(点A在第一象限),M,N是椭圆上位于直线l两侧的动点,若∠MAB=∠NAB,求证:直线MN的斜率为定值.
2 解法探究

2.1 第(1)问解析
又a2=b2+c2,所以a2=4,b2=3.
2.2 第(2)问解析
思路1利用两点间的斜率公式.





因为∠MAB=∠NAB,所以kAM+kAN=0.



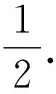

思路2韦达定理.
解法2(斜截式)设lMN:y=kx+m,代入3x2+4y2-12=0,得(3+4k2)x2+8kmx+4(m2-3)=0.

因为∠MAB=∠NAB,所以kAM+kAN=0.
①
将x1+x2与x1·x2代入①式,整理,得
(2k-1)(2k+2m-3)=0.
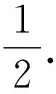
评析解法1采用了点差法,运算较为简单,解法2考虑到探求直线MN的斜率,直奔主题,采用了直接设直线MN斜截式方程的方法,思路清晰,但最后整理化简过程技巧性强,方程组的思想和韦达定理的应用是解法2的主体.结论中的定值是1/2,而椭圆的离心率也是1/2,这是一种巧合还是有一般性的规律?为此,师生共同编撰并探究了下面一道试题.
3 变式探究

证明设M(x1,y1),N(x2,y2),直线lMN:y=kx+m,代入16x2+25y2-400=0,得
(16+25k2)x2+50kmx+25(m2-16)=0.
又△=2500k2m2-100(16+25k2)(m2-16),
由△>0,得m2<25k2+16.
由韦达定理,得
因为∠MAB=∠NAB,
所以kAM+kAN=0.

又y1=kx1+m,y2=kx2+m,

=0.
②
将x1+x2与x1·x2代入②式,整理,得
75k2+25(m-5)k+3(16-5m)=0.
即(5k-3)(15k+5m-16)=0恒成立.


评析本题也可以采用点差法进行求解,读者可以自行验证,此处直线的斜率依然等于椭圆的离心率.将该变式探究和前面试题进行比较可得,直线MN的斜率总为定值,而且这个定值等于椭圆的离心率[2],可见该结论应该具有一般性,可以进行推广.
4 结论推广

证明设M(x1,y1),N(x2,y2),直线lMN:y=kx+m,代入b2x2+a2y2-a2b2=0,得
(b2+a2k2)x2+2a2kmx+a2(m2-b2)=0.
又△=4a4k2m2-4a2(b2+a2k2)(m2-b2),
由△>0,得m2 由韦达定理,得 因为∠MAB=∠NAB,所以kAM+kAN=0. 又因为y1=kx1+m,y2=kx2+m, 整理,得 ③ 将x1+x2与x1·x2代入③式,并化简得 a2ck2+a2(m-a)k+c(b2-am)=0. 所以(ak-c)(ack+am-b2)=0恒成立.