基于伪foF2的短波频率预报方法及精度分析

陈训韬

（广州通信研究所，广东 广州 510310）

0 引言

短波天波通信因受电离层影响，具有典型的窗口特性[1]，对于给定时间给定的通信链路，存在特定最高可用频率（Maximum Usable Frequency，MUF）。使用超过MUF 的频率，即使增加发射设备功率，由于大部分电波能量将传播至更远的地点或穿透电离层，对端的接收设备也很难收到足够能量的信号。因此短波通信通常需要进行频率规划及频率动态调整[2][3]。ITU-R P.533[4]据历史探测数据给出了对短波通信链路MUF 的预测模型，有研究机构针对中国地区也给出了更加精确的长期预测模型[5]。但由于统计结果本身的波动性，这些模型在实际使用时仍不够精确。为提供实时短波信道MUF 数据，斜向探测是常用的手段。由于探测链路与通信链路通常不重合，基于探测数据预测通信链路MUF 值的问题是短波信道分析的研究热点。实时探测数据的重构方法包括等效太阳黑子数法[6]、Kriging 重构方法[7][8]、神经网络重构法[9][10]，基于斜向探测数据[11]，以及基于多体制探测数据融合方法[12]等。其中基于斜向探测数据进行外推预报的方法因使用方便、精度高而更为流行。这些研究表明电离层对短波通信信道MUF 的影响可主要根据链路控制点电离层参数来推算。通过已知短波探测链路的斜向探测数据，可以估计该链路控制点的链路参数，并进一步推算未知通信链路控制点的电离层参数，从而得到该链路MUF。

文献[11] 首先提出了基于实测的斜向探测数据进行实时高频通信MUF 预测的一种实用方法，以斜向探测的短期预报数据为基础进行电离层参数分析，结合ITU 高频频率预报方法实现了MUF 实时预报，统计均方根误差为1.41 MHz，相对误差为10.09%。

但文章未给出预报误差与链路条件之间的关系，对预测方法的在工程中的实际应用造成一定局限。

由于短波天波传输链路中控制点F2 层临界频率foF2与MUF 关系密切[13][14]，可以考虑利用不同链路foF2关系估算对应MUF 参数关系。短波Chirp 探测数据是通过短波斜向探测获取MUF 参数目前精度最高的实测方法。本文利用2021 年某专项短波天波试验中短波Chirp 探测数据，分析对比了不同链路反射点的经度差、纬度差、距离等参数与预测精度之间的关系，以及链路不同的绝对时间、经度、纬度等对预测的影响，给出基于伪foF2预测MUF 的方法及适用条件，对利用Chirp探测数据进行短波MUF预测在工程上的实践将起到指导意义。

1 基于伪foF2的短波MUF预报算法

ITU-R P.533 提供的模型，已知控制点foF2、M(3000)F2参数，可以得到各天波传输模式的F2 层基本MUF 长期预报值。基于此原理，可以利用斜向探测数据提取F2 层MUF 数据，反演探测链路控点的电离层参数，计算这些参数与长期预报参数的关系，并将此关系应用到未知通信链路上，通过未知通信链路的F2 层基本MUF 长期预报值推算当前值。具体步骤如下。

1.1 短波链路控点电离层参数长期预测值获取

ITU-R P.1239[15]给出了foF2、M(3000)F2的月平均值长期预测公式。基于世界各地大量地面站的电离层垂直入射探测结果生成数字映射，给出了foF2和M(3000)F2月度平均值等参数与地理位置、时间、太阳活动的级数展开系数表。

数字映射的形式为

其中：

Ω：要映射的电离层特性

λ：地理纬度，-90°≤λ≤90°

θ：地理东经度，0°≤θ≤360°（θ为格林威治子午线以东的度数）

T：世界时，以角度表示，-180°≤T≤180°

H：日变化的谐波的最大阶数

U2j,k、U2j-1,k可写为Us,k(s=2j或2j-1)。国际电联无线电通信第3 研究组给出了以经纬度为单位的网格点在指定月份和太阳活动强度上的数字映射中Us,k系数的参考表。网格点上不同日期和太阳活动强度的系数可以采用线性差值或外推得到。网格点之间任意位置系数可以使用ITU-R P.1144[16]提供的双线性插值方法计算得到。Gk(λ,θ) 为地理坐标函数，可使用ITU-R P.1239 附件1 给出的方法计算Gk(λ,θ)取值。

通信链路控点与电波传播模式有关。基于实践经验，本文仅考虑低阶传播模式基本MUF 的预测。对于传输距离在F2 层单跳最大跳距dmax以内的短波通信链路，取链路的中点作为其控点。对于超过单跳跳距的链路，在分别距发射点和接收点位置为F2 层最低阶跳距二分之一的两处地点之中，选取链路损耗较小的传播模式对应的地点作为外推计算的对象，利用式(1) 获取其电离层参数长期预测值。

1.2 控点伪foF2计算

foF2、M(3000)F2的获取可分别采用固定一个参数，对另一个参数进行反演的方法获得。仿真计算结果表明，M(3000)F2的变化对MUF 外推预报影响不大，为此M(3000)F2可采用长期预报值不变，用控点不同的foF2数据拟合探测结果得到的实测MUF 数据，来反演探测链路控点伪foF2数据。反演算法如图1 所示。

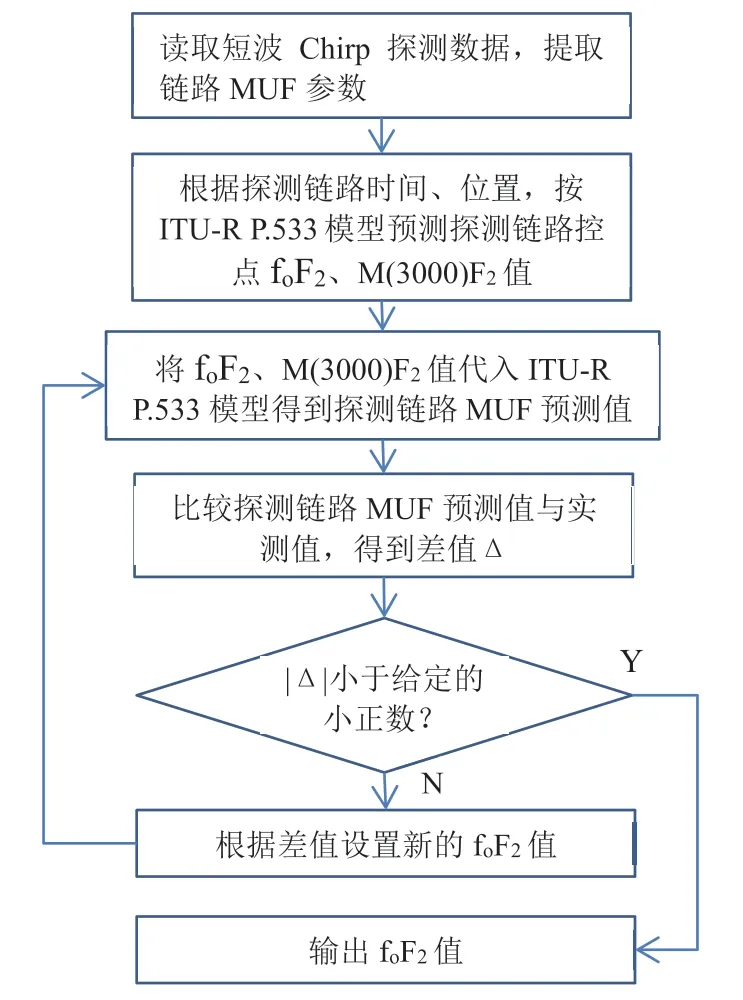
图1 探测链路控点伪foF2计算算法

1.3 基于伪foF2推算MUF

由于同一天太阳活动的相关性较强，在探测链路与要预测的通信链路的控制点距离相差不大的情况下，利用探测链路的foF2推测通信链路的foF2，并进一步预测其F2 层MUF 具有可行性。

重构通信链路控制点处foF2的常用方法有等比加权方法[17]、距离倒数加权重构方法[18]、克里格方法[19]等。这些方法的主要思路为利用多个已知点foF2数据，按照未知点与这些已知点的距离关系加权计算未知点foF2，如下式：

其中W(di) 为不同距离的权重系数。在已知点较少时，得到的预测结果基本与已知点的foF2等价，容易引入较大的误差。这里基于长期预测计算的foF2与反演得到的伪foF2之间关系反映了电离层参数实际值与预测值变化，给出一种在只有单个已知点伪foF2数据情况下推算未知点foF2及MUF 的方法。

以下标0 表示未知点，以下标1 表示已知点，加撇号的值表示反演值，不加撇号的值表示长期预测值，令

其中已知链路与未知链路控点foF2长期预测值可利用ITU-R P.533 模型计算得到，已知链路控点的foF2反演值采用上节提供的方法计算，从而可以得到未知链路控点foF2值。在此基础上，利用ITU-R P.533 模型计算未知链路F2 层MUF 值，如下式所示。

其中n为模的阶数，fH为在300 km 高度由适当控制点算出的电子回转频率。

其中：

公式中的d和dmax，单位都为km，C3000为当d=3000 km时Cd的值，x为foF2/foE 或2，选较大者。

由于该方法仅需要一条链路的测量数据，在一些不方便联网测量的移动工作场景下也可以有效完成计算。在存在多条探测链路的情况下，如果所有探测链路的控点外接组成的球面多边形不能包含与要预测的通信链路控点，或者说这些控点电离层特征参数的加权平均值不能准确代表预测链路控点的电离层特征参数，那么选择最近的控点采用本方法就可以减少引入其它控点计算所增加的误差，因而有更高的参考价值。

2 基于实测数据的验证及适用条件

下面采用2021 年10 月某短波探测试验数据对算法进行验证，并分析算法精度与控点距离的关系。

本次试验中，电离层探测采用Chirp 探测发射机与接收机，发射功率100 W；收发天线采用四线倒V 宽带天线，各试验地点中同时存在收发的，收发设备位置间隔10 km 左右；采用100 kHz/s 的速率进行2 MHz～30 MHz信道探测，每5 至20 分钟统计一轮数据，通过对接收的电离图分析提取F2 层MUF 参数。探测链路的各台站包括宝鸡、成都、南京、怀化、呼和浩特、昆明、兰州、广州、拉萨等。以宝鸡、成都为探测发射站，其余为探测接收站点，一共存在14 条探测链路，记各条链路控制点为C1，C2，…，C14。试验一共开展了15 天，由于期间存在设备维护、资源协调等间断，共处理有效探测数据590 条。

在得到的结果中，采用前文提到的方法，用其中一条探测链路结果得到的F2 层MUF 数据，预测同一时刻其它链路的F2 层MUF 数据，并与实测数据对比，分析预测的精度。为考察预测精度与链路间控点距离的关系，在进行预测计算的同时，一并计算探测链路与预测链路控点之间的距离。

几组典型的预测结果、实测结果与长期预报计算结果的对比情况如图2 至图5 所示。

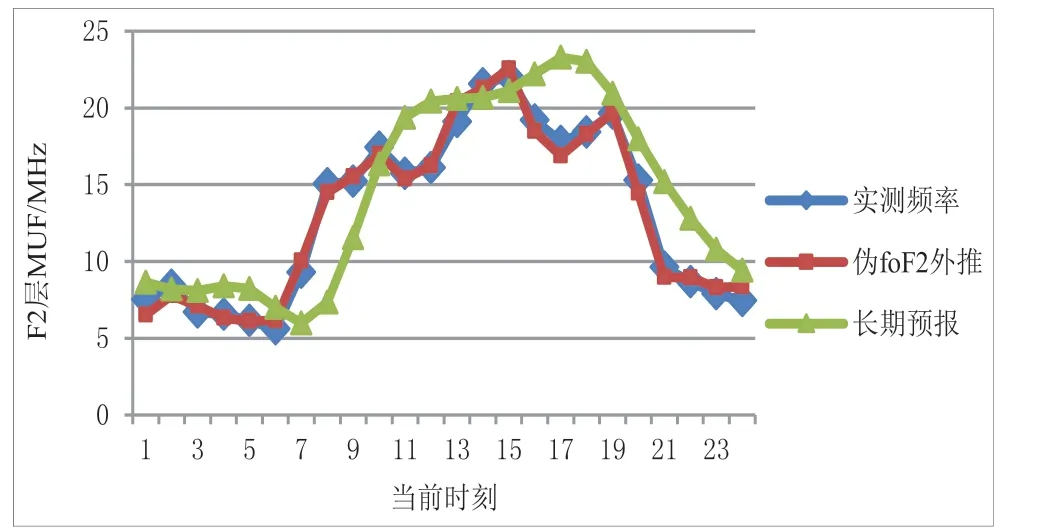
图2 南京收宝鸡预测南京收成都（10月2日）

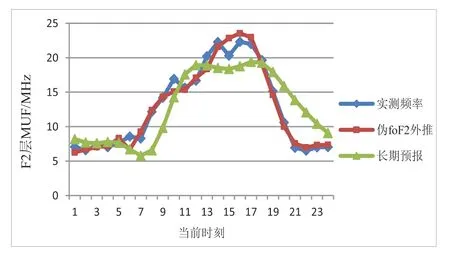
图3 南京收成都预测呼和浩特收成都（10月2日）

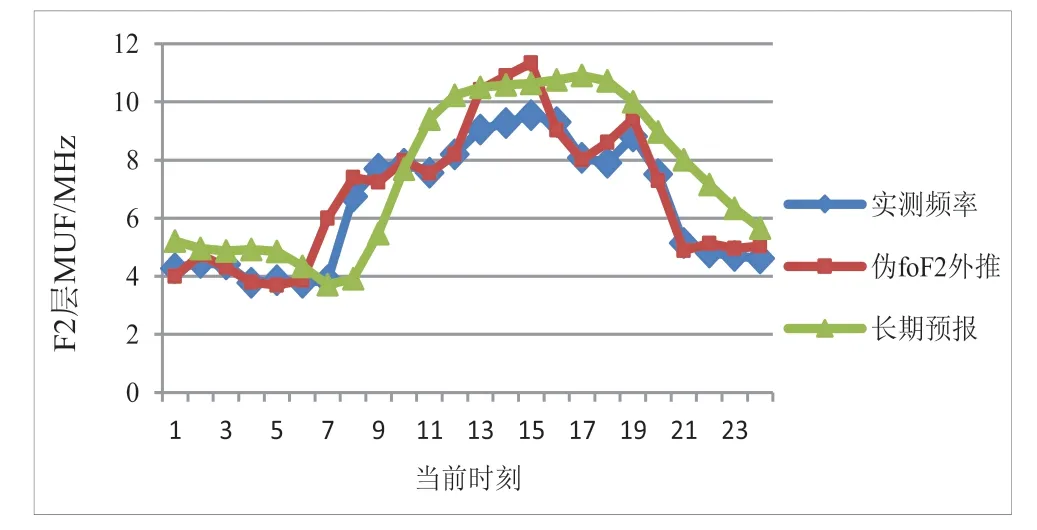
图4 南京收宝鸡预测兰州收宝鸡（10月2日）

图5 南京收成都预测拉萨收成都（10月2日）

图中可以看出，采用伪foF2外推方法得到的F2 层MUF 预测结果在已知链路与预测链路控点相距较近时与实测值较为接近，在控点距离增加时误差逐渐增大。

为进一步分析控点距离对不同链路F2 层MUF 相关性的影响，确定外推方法的适用条件，计算各探测链路两两组合的控点距离、经度差、纬度差，以及在此情况下各链路两两间24 小时实测F2 层MUF 值相关性。

相关系数r由下式给出。

其中X 与Y 为相同时刻两条探测链路实测的24 小时F2层MUF 值序列。

表1 给出了各条链路两两之间24 小时MUF 相关系数与控点距离、控点经度差（绝对值）、维度差（绝对值）的对照关系表。从表中可以看出，各条链路的MUF 之间呈现明显的正相关特性，这种相关性为链路MUF 外推算法提供了依据。而这种相关性随链路控点间距离、经度差、纬度差增加而减弱，说明链路外推算法需考虑适用条件。

为判断控点距离对MUF 相关性的影响，利用流行统计软件提供的分析功能进行多项式趋势线拟合[20]，给出各探测链路控点间距离与其MUF 相关系数之间的关系如图6 所示。从多项式拟合的趋势曲线可以看出，在400 km 以内的控点距离条件下，不同探测链路的MUF 具有很强的相关性。而随着控点距离增加，MUF 相关性逐渐下降。

控点距离增加意味着经度差增加与纬度差增加，为对比控点间经度差、纬度差、距离等不同参数对链路MUF相关性的影响，从而决定采用何种因素设定外推算法的适用条件，根据表1 进一步计算上述3 个参数与MUF 相关系数的相关系数，分别得到结果为-0.67、-0.37 和-0.87。可以看出，经度差、纬度差及控点距离与MUF 相关系数均为负相关，经度差比纬度差负相关性更强，但依然不如控点距离的负相关性强，因此取控点距离作为相关性的综合影响因子更可行。

采用伪foF2法预测F2 层MUF 与Chirp 探测实测数据的误差与预测链路和已知探测链路之间控点距离的关系如图7 所示。可以看出，随着控点距离增加，误差平均值与标准差均逐渐增大。控点距离0～500 km 时日均误差小于正负1 MHz，标准差小于2 MHz，特别是控点距离在0～300 km 时，标准差小于1.5 MHz；控点距离500～1500 km时平均误差绝对值小于2 MHz，标准差小于3 MHz。

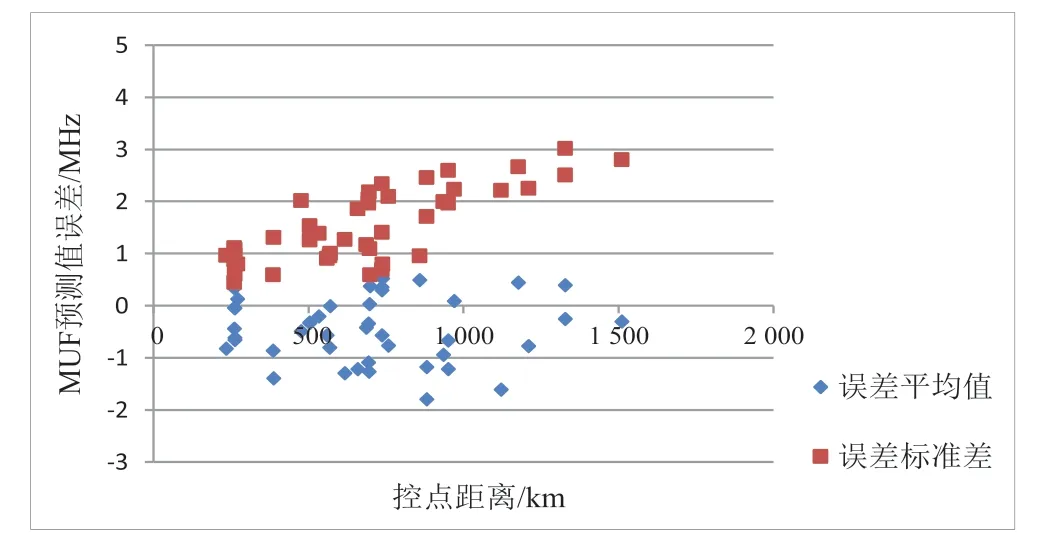
图7 伪foF2法误差与控点距离关系

为与之对比，采用ITU-R P.533 提供的长期预报方法进行计算，其与Chirp 探测实测数据的误差与预测链路和已知探测链路之间控点距离的关系如图8 所示。两图对比可以看出，在距离较近时，特别是在300 km 以内时，伪foF2法预测误差均值与标准差均明显低于长期预报方法，随着控点距离增加，这种差别逐渐缩小。到了1 500 km，伪foF2法已没有明显优势。

图8 长期预报法误差与控点距离关系

3 结束语

本文针对短波Chirp 探测数据在短波频率预报中的应用给出一种基于foF2的工程计算方法，并根据历史试验数据对其不同使用条件下的预测精度给出了分析。结论如下。

1）方法优势

该方法的优势是工程实现简便，精度高，实用性较强。

基于伪foF2的计算方法可以利用单条链路短波探测数据外推其它反射点相近链路的F2 层MUF，精度较高。其中单条链路MUF 的探测方法可采用Chirp 探测、脉冲探测等多种探测方式获得。计算量小，实测在普通PC（配置为Intel® i5-6500 CPU @3.20GHz，8GB 内存）上使用流行仿真计算软件完成24 次外推计算时间小于1 s。

探测链路与外推链路控点距离小于500 km 时，预测误差平均值绝对值小于1 MHz，标准差小于2 MHz，小于300 km 时，标准差小于1.5 MHz，明显优于长期预报的小于4 MHz 的标准差。

与其它同类需要融合多条链路探测数据重构区域F2层临界频率的预测算法相比，由于仅需要在探测接收地点进行数据处理，工程上更加便于实现。特别是对于车、船等移动用户来说，平台与其他节点数据交换受限，不便采集多条探测链路数据，采用本方法可只利用所在平台探测数据实现到多个固定短波台站的频率优选，以提高可通率，缩短建链时间，实用性更强。

2）局限性

本方法的使用受探测链路与未知预测链路反射点距离及传播模式中天波跳数的限制。

在已知探测链路与未知预测链路反射点距离较远时，本方法与长期预报相比不具备优势。实验表明，反射点距离在500 km 至1 000 km 时，本方法预报误差平均标准差为2 MHz 左右，略优于长期预报方法的3 MHz，反射点距离在1 000 km 至1 500km 时，两种预报方法误差平均标准差均在2.5 MHz 左右。

受限于试验数据样本条件，本研究给出的方法仅对中国地区中高纬度F2 层1 跳情况进行了验证，对于全球其它地区以及多跳情况，仍需开展进一步试验与研究。

为此建议本方法的应用条件为已知探测链路与未知探测链路间控点距离不大于500 km，最好不大于300 km。