热处理工艺模拟专用材料数据库的设计与实现

张伦凤, 王治涵, 赵俊渝, 安 康, 徐 骏, 顾剑锋

(1. 上海交通大学 材料改性与数值模拟研究所, 上海 200240;2. 重庆齿轮箱有限责任公司, 重庆 402263)

自20世纪70年代起,许多发达国家都相继开展了材料数据库的相关研究。至今,以欧美、日韩等为代表的传统工业国家已经拥有了一定数量的材料数据库,其中包含了黑色金属、有色金属、复合材料、陶瓷材料、功能材料等各种材料的成分、相图、晶体结构、性能参数等数据[1]。我国从80年代初期才开始进行材料数据库的研发,众多高校、科研院所以及生产机构也先后建立了多种材料数据库[2-4]。但是,早期的材料数据库主要以离线型为主,多用于数据存储和研究,存在材料种类较少、数据结构完整性较差以及数据库功能不完善等问题。并且,传统材料数据库多数以化学成分作为数据库的主要结构体。但在热处理过程中,材料的各项物理参数与其微观组织关系密切,无法通过单一化学成分确定参数变化。因此,现有设计模式无法满足热处理工艺模拟对参数的需求。

此外,由于材料数据库的受众人群并不广泛、材料试验周期一般较长且花费昂贵,导致现有材料数据库大多面临多种数据缺失的情况,若仅仅对已有数据进行检索提取,则往往无法满足仿真计算的使用需求,同时也使得材料数据库的使用十分受限。因此,对数据库的数据提取功能提出更高的要求。美国于2011年启动的材料基因组计划涵盖了数据储存与共享、计算材料、新材料设计、软件开发等多个方面[5]。其中有一项重要的思想就是利用数据挖掘手段,从已有的数据集中发掘更多的材料信息以加速材料设计。数据驱动机器学习是一种重要的数据挖掘方法,可以应用于分类和回归,且已被成功引入材料工程的工艺优化、设计新合金和模拟性能,优化数值模拟的准确性,对材料研发和实际生产具有重要的指导作用,加速了材料研究和设计的进步[6-7]。

鉴于此,本文针对热处理工艺模拟的特点,设计了以化学成分与微观组织为主的数据结构体,引入机器学习实现数据自动匹配提取功能,结合数据库设计原理和热处理相关材料信息模型理论,开发了一款专用材料数据库,涵盖热物性、相变及其附加反应等各类参数信息,支持数据存储、数据检索以及数据自主输入输出等功能,旨在为数值模拟提供专业且丰富的材料数据信息,为热处理工艺的制定提供理论指导。

1 材料数据关系模型

热处理工艺模拟所需的材料数据十分繁杂,涵盖热物理性能、相变及其附加的应力应变和潜热作用等各类参数信息,难以通过简单数据结构将其完整地构建出来。因此,材料数据库中数据表的设计是实现材料数据库功能的关键一环。

在热处理过程中,材料的微观组织发生改变,而材料的各项力学性能与物理性能又与其微观组织密切相关,例如材料由奥氏体转变为马氏体后,其屈服强度会发生显著变化。因此,材料的各项热物理性能需要按不同微观组织分类记录。本文将化学成分和微观组织共同作为材料热物理性能数据的基本结构体,如图1所示。其中,Chemical包含了碳、氮、氧等化学成分信息,Microstructure包含微观组织以及类别信息,二者分别通过外键与Material相互关联,即每一数据结构体对应某一材料的一种微观组织,如20CrMnTi钢—奥氏体、45钢—马氏体等。

图1 材料信息结构的关系模型Fig.1 Relationship model of material information structure

其次,热处理工艺模拟通常需要计算相变产物的体积分数,而不同类型的相变反应采用不同的动力学模型来计算。例如,钢中过冷奥氏体的等温分解可以使用JMAK模型或Avrami模型,而马氏体相变则使用K-M方程。JMAK模型的相变体积分数f为,

f=Fmax·[1-exp(-Atn)]

(1)

A=Kd·(Tc-T)m·exp(-Q/RT)

(2)

式中:Fmax为最大转变分数;Tc为相变临界温度;T为温度;t为时间,R为气体常数,取8.314 J/(mol·K);A、Kd、n和m均为模型常数;Q为激活能。

Avrami模型的相变体积分数f为,

f=Fmax·{1-exp[-b(t-t0)n]}

(3)

式中:Fmax为最大转变分数;t0为孕育期;t为时间;b为模型常数。

K-M方程的相变体积分数f为,

对于冷却过程:

f=Fmax·{1-exp[-aM·(Tc-T)]}

(4)

对于加热过程:

f=Fmax·{1-exp[-aM·(T-Tc)]}

(5)

式中:Fmax为最大转变分数;Tc为相变临界温度;T为温度;aM为模型常数。

为简化上述操作,本文设计了一种较为灵活的数据结构,以满足多种相变模型参数的存储。以工程上最常用的TTT曲线数据为例(如图2所示),相变信息被定义在表Phase transform中,包括新相、母相、奥氏体转变时间等。表TTT model包括了TTT曲线数据中的最大转变分数Fm、相变开始时间T1以及相变结束时间T99参数信息,其中外键Variable ID连接了表Variable group,可存储TTT曲线中各个参数,以此来描述这些参数随着温度、等效应力、等效应变和外部压力的变化而变化。

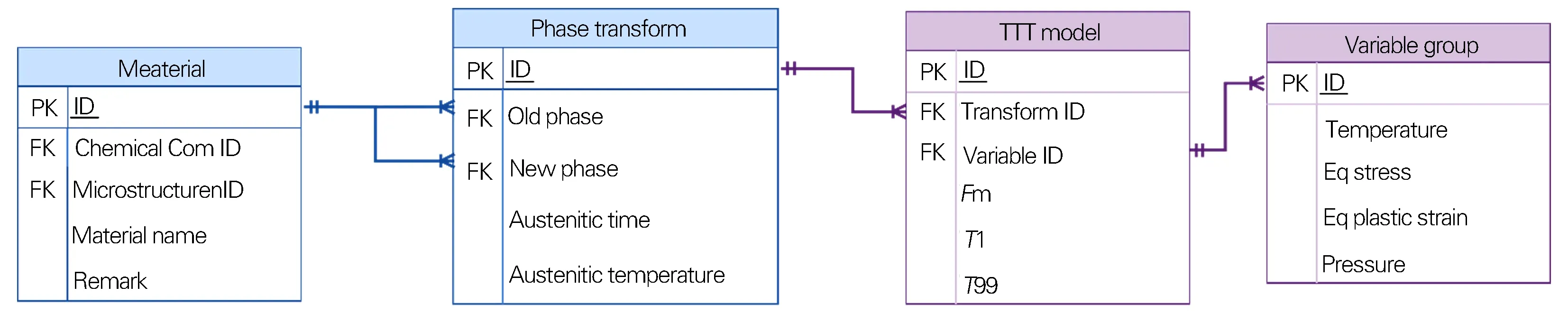
图2 TTT模型信息的关系模型Fig.2 Relationship model of TTT model information

本文数据库中的材料信息按微观组织、化学成分—材料—热物理性能和相变动力学模型参数的3级结构进行存储。每种材料包含热物理性能和力学性能,它们通过外键连接,同时又作为相变反应中的新相或者母相连接到相变动力学。其结构内容以及结构间的相互关系如图3所示。

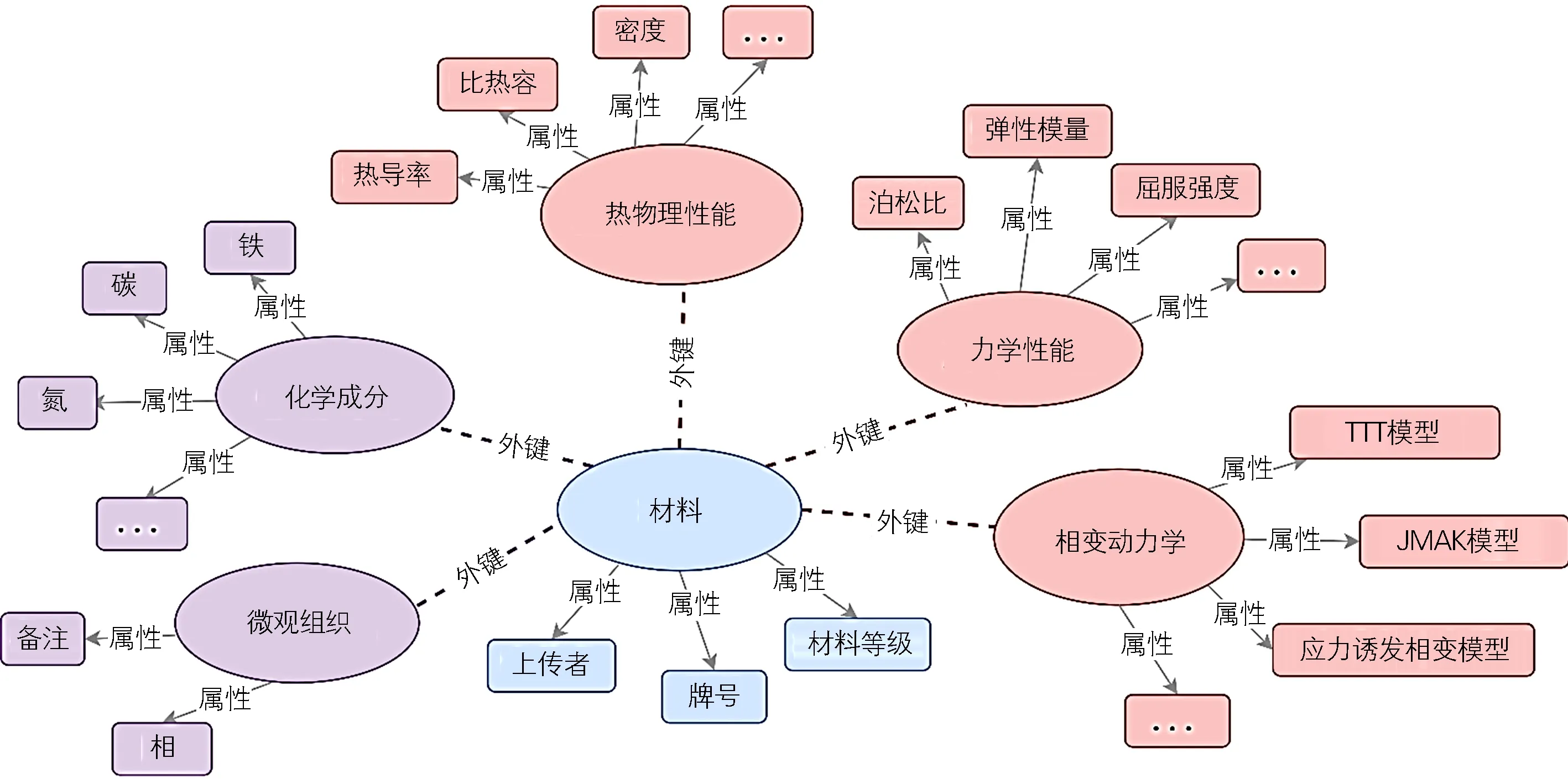
图3 材料数据库表结构示意图Fig.3 Schematic of table structure in material database

其中,热物理性能包含各相的密度、比热容、热导率、碳扩散系数和氮扩散系数,力学性能包括泊松比、屈服强度、热膨胀系数、相对膨胀系数、弹性模量和高温蠕变参数;相变动力学结构体可用于描述某一材料的一项相变反应,如奥氏体化、马氏体转变等,不同类型的相变可以由不同的数学模型进行定量表征。同时,在计算应力场和温度场时,还需要提供应力诱发相变、相变应变、相变塑性、相变潜热等数学模型。

2 材料数据库的设计方案

本材料数据库系统采用了B/S(Browser/Server)架构设计,如图4所示。相比于传统的C/S(Client/Server)架构,B/S架构基于浏览器实现,具有无需安装、无需用户维护更新和跨平台等多种优点,且数据通过HTTP协议进行传输,更加利于共享引用。针对热处理工艺模拟所需材料参数的繁杂多样性,系统使用了逻辑关系更加清晰的关系型数据库MariaDB,同时在数据输入模块中采用DRY (Don’t repeat yourself)思想[8],避免研究人员重复录入相同信息。

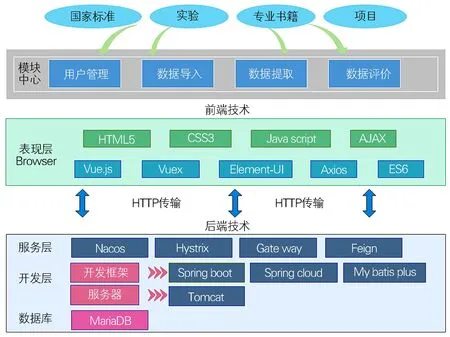
图4 材料数据库的整体架构示意图Fig.4 Schematic of overall framework of the material database

除了基本的数据存储、数据管理以及数据检索等功能外,本材料数据库更加关注数据的有效提取。为此,设计了相应的功能模块,引入多种机器学习算法,以提升数据的可用性与完整性。

本材料数据库目前已收录26种常用材料的113种微观组织参数,数据条目达到了31 958条,如图5所示。其中包含了材料各种微观组织对应的密度、比热容、弹性模量、泊松比、热导率和屈服强度、热膨胀系数、相对相膨胀系数以及TTT曲线等数据。这些数据的来源主要为实测、文献资料[9]以及第三方材料数据计算软件,如JMatPro等。

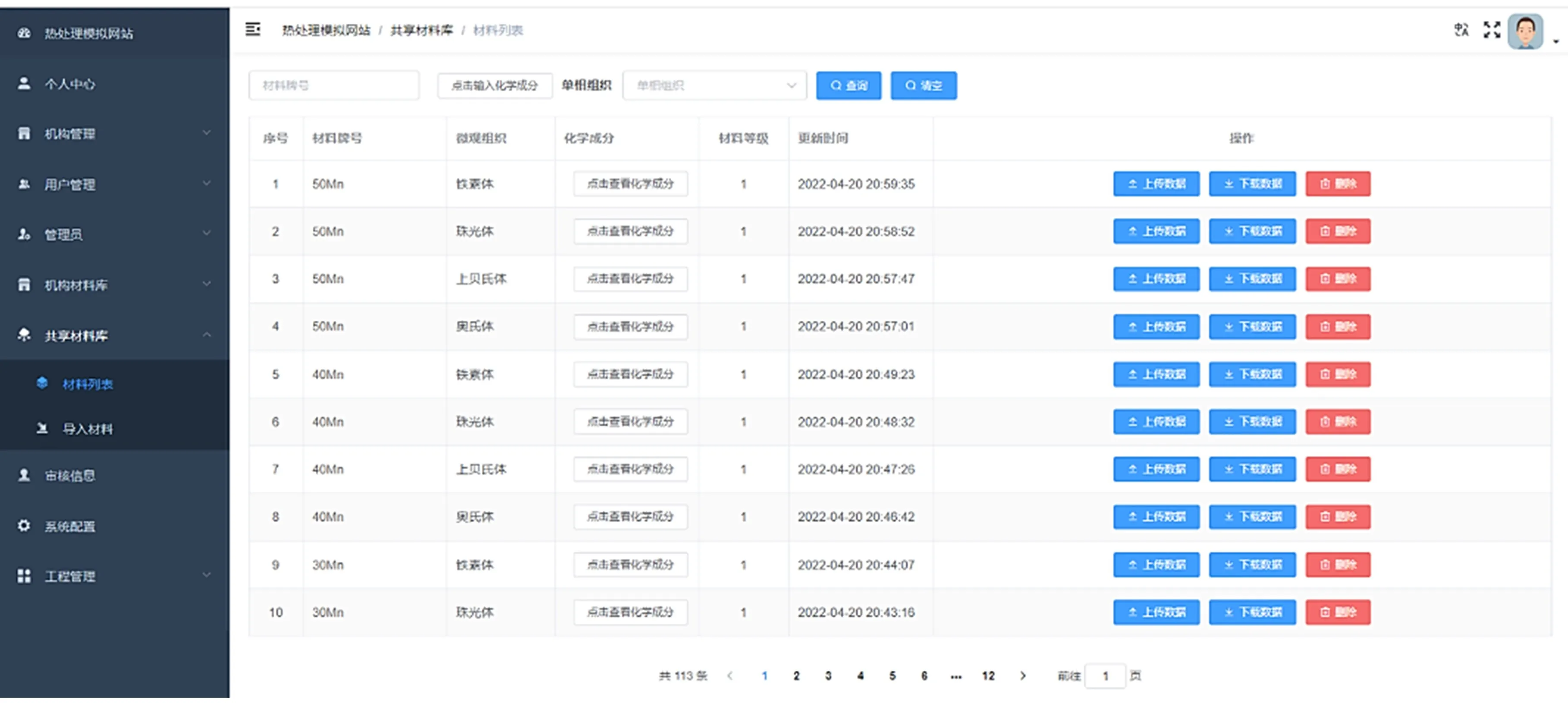
图5 数据库的材料列表Fig.5 Materlal list of database

3 基于机器学习的数据提取机制

3.1 机器学习算法

本数据库最大的特点就是在数据提取中引入了机器学习算法。所谓机器学习,是通过给定的数据集(称为训练集)来进行模型训练,从而掌握数据规律,预测未知数据或做出判断,在材料性能的预测方面有了广泛的应用[10-12]。通常,机器学习分为3种算法:监督式学习、无监督式学习和强化学习。其中,监督式学习可以利用一个或多个自变量来预测一个或多个因变量,使得其在材料性能预测方面应用广泛。监督式学习中也包含许多种算法,每种算法均可独立用于数据的预测,其中应用较多的算法有多元线性回归、贝叶斯线性回归、决策树和随机森林4种方法。

多变量线性回归是分析直线或超平面形式输入和输出之间线性关系的常用方法,可以产生基于多个变量的响应,认为输出变量y与输入变量X=(x1,x2…xn)线性相关,θ为待求值[13]:

yθ(X)=θ0+θ1x1+θ2x2+…+θnxn

(6)

贝叶斯线性回归同样是线性模型的一种。贝叶斯线性回归的预测结果不是一个固定值,而是一个分布,对于给定样本特征X=[X1…Xn]T,认为样本标签Y=[y1…yn]T满足:

y=ωTX+

(7)

决策树是一种模仿具有随机数量的树枝和节点的树结构,采用自顶向下的递归方法,其基本思想是以信息熵为度量构造一棵熵值下降最快的树,直至叶子节点处的熵值为0[15]。

随机森林由多个决策树组成,每棵树取决于独立采样的随机向量值,并且森林中的所有树都具有相同的分布。预测结果可以通过每个随机树结果的平均值或众数获得。相对于决策树,随机森林可以处理高维数据,不容易陷入过度拟合[16]。

3.2 模型建立与验证分析

机器学习算法的有效性不仅与具体参数对象相关,同时也有依赖于训练集。为取得各项参数最适用的机器学习算法,在此采用k-fold交叉验证方法,就上述4种机器学习算法对各项热处理材料参数开展对比试验,如图6所示。将所有数据平均随机划分为5个数据集,并选取其中一个作为验证集,其余4个作为训练集,分别采用4种机器学习算法进行一次模型训练与验证。依次轮换验证集,总计进行5轮测试,综合所有测试结果开展有效性评价。同时,考虑到不同材料类型对数据有效性的影响,分别对碳素钢和铝合金数据进行了同样的验证对比。

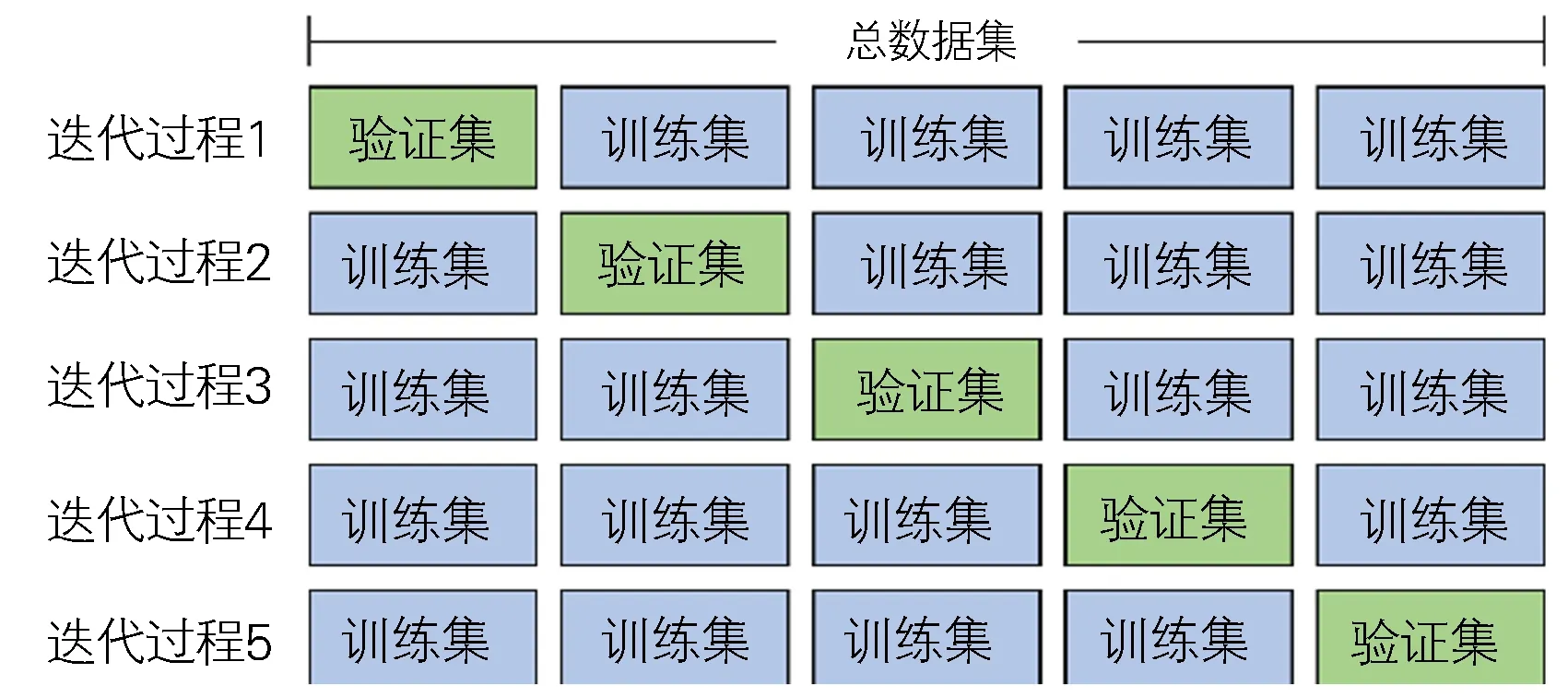
图6 5-fold交叉验证试验Fig.6 Five-fold cross validation for machine learning

在验证对比过程中,将每一轮验证的平均绝对百分误差[7](Mean absolute percentage error, MAPE)作为机器学习模型有效性的基础评价指标,其定义为,

(8)

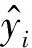
在此,使用5轮交叉验证的MAPE均值E来评估模型的准确性,方差D来评估模型的稳定性。

4种机器学习模型对材料各项参数预测的有效性验证结果如图7所示。其中,对于密度来说,各模型预测结果的均值E均在1%以下,方差D均在10-6以下,预测效果极好;而对于比热容、热导率、泊松比、弹性模量、屈服强度、热膨胀系数,随机森林和决策树算法的均值E均在7%以下,方差D均在10-4下,预测效果较好;但贝叶斯线性回归和多元线性回归均值和方差较大,特别地,二者屈服强度的均值E均达到120%,预测效果较差,如图7(a,b)所示。

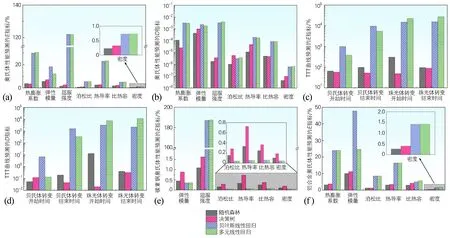
图7 4种机器学习模型对材料参数预测结果的E和D指标(a,b)奥氏体组织的性能参数;(c,d)TTT曲线的模型参数;(e,f)区分材料种类后奥氏体组织的性能参数Fig.7 E and D criteria of prediction results of material parameters by four machine learning models(a,b) property parameters of austenitic structure; (c,d) model parameters of TTT curve; (e,f) property parameters of austenitic structure after distinguishing materials

针对相变动力学中的各项模型参数(TTT曲线),两种线性模型的均值E均在300%以上,这是因为相变动力学模型参数具有极强的非线性特性;而决策树算法的均值E在50%上下浮动,方差D在10-1以下,在4种算法中效果最好,如图7(c,d)所示。

此外,在对材料种类进行分类后,多元线性回归和贝叶斯线性回归算法的预测效果提升显著,如铝合金屈服强度的均值E降低至50% 以下,如图7(e,f)所示。由此表明,材料类型对于材料各项数据具有显著影响,不同类型材料其对应材料数据的变化规律具有显著的差异。

依据上述结果,本文获得基于机器学习算法的数据提取策略。首先,按照材料类型、微观组织分别划分数据集,并选用对应的类型和微观组织开展数据集训练与预测。其次,不同的材料数据对象适用不同的机器学习算法,如预测密度、比热容、热导率、泊松比、弹性模量和屈服强度时,可优先采用随机森林算法,而预测TTT曲线模型参数时则应采用决策树算法。同时,现有试验表明,多数材料数据具有一定的非线性特性,因而不适合采用多元线性回归或贝叶斯线性回归模型算法进行学习与预测。

4 结论

本文自主开发了一款热处理工艺模拟专用的材料数据库,主要特性如下:

1) 该专用材料数据库系统实现了各类物性参数与相变动力学参数的有效存储与管理,具备数据检索、自主上传和自动匹配提取等功能,能够为热处理工艺模拟提供良好的数据支撑。

2) 该数据库系统引入了基于数据挖掘技术的机器学习算法,通过现有数据集的学习与对比,可确定有效的数据提取策略,解决了热处理工艺模拟中普遍存在的数据缺失问题。