“杠杆法”巧解复杂的平衡问题

熊高云

(江西省南康中学北校区,江西 赣州 341400)

(2022·浙江·模拟预测)如图1,两根等长的细线一端拴在同一悬点O上,另一端各系一个带电小球,两球的质量分别为m1和m2,已知两细线与竖直方向的夹角分别为45°和30°.则m1与m2的比值为( ).

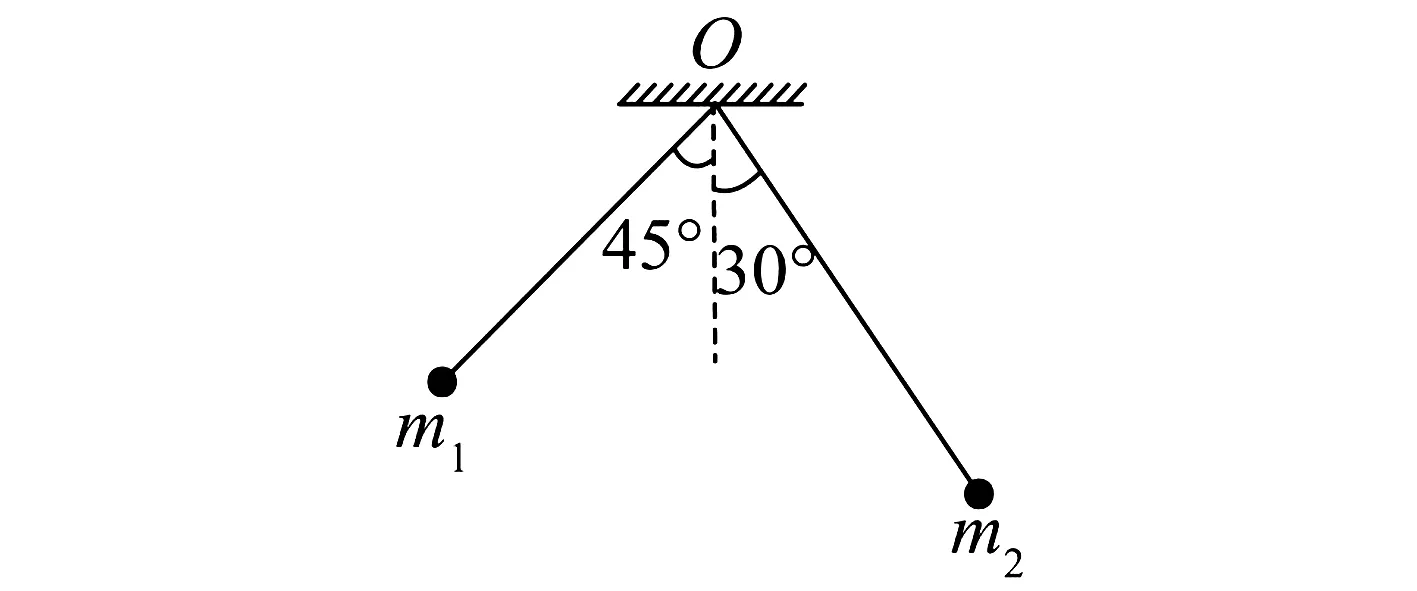
图1 例题图

答案:A

1 解法探究

详解(1)常规解法一(正交分解法):对两个球分别受力分析,如图2所示.

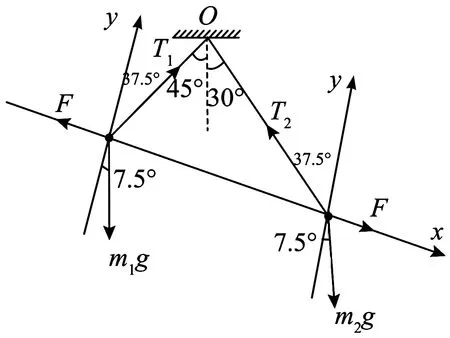
图2 受力分析、正交分解图

根据平衡条件,对m1,有

m1gcos7.5°-T1cos37.5°=0

F-m1gsin7.5°-T1sin37.5°=0

对m2,有

m2gcos7.5°-T2cos37.5°=0

F+m2gsin7.5°-T2sin37.5°=0

联立解得

故选A.

(2)常规解法二(相似三角形):对两个球分别受力分析,如图3所示,设两等长的细线长度为L,则

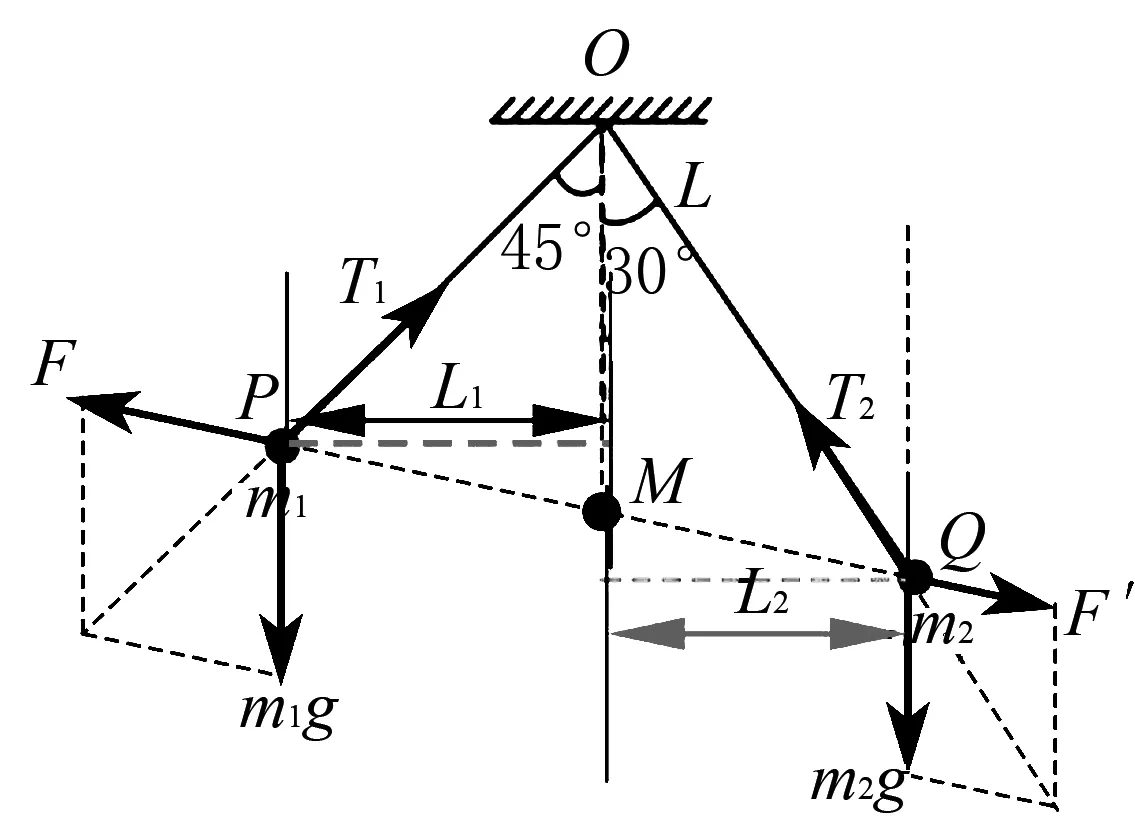
图3 受力分析、相似三角形图

由相似三角形可得

由于F与F′为两带电小球间的相互作用——静电力,所以大小相等,方向相反,联立以上两方程可得

由几何关系可得

整理可得

m1g·L1=m2g·L2

由图1可知,L1和L2分别为两小球到转轴OM的距离即为力臂,由m1g·L1=m2g·L2可知,此类问题可用“杠杆法”快速准确进行处理[1].

2 原理及适用条件

“杠杆法”原理为将几个相互作用的物体看成一个整体,(这样可以省去分析相互作用物体间的内力),再将“悬点”作为系统转动的支点(或转轴),(这样做的目的是使过支点的绳子拉力或支持力的力距为0,简化力距平衡方程).最后对系统列力距平衡方程即可快速准确的求解.

由“杠杆法”原理可知,此方法适用于存在“悬点”的系统问题处理,具体地讲可以是高中物理中的“双单摆”模型、“碗球”模型[2].

3 实战应用

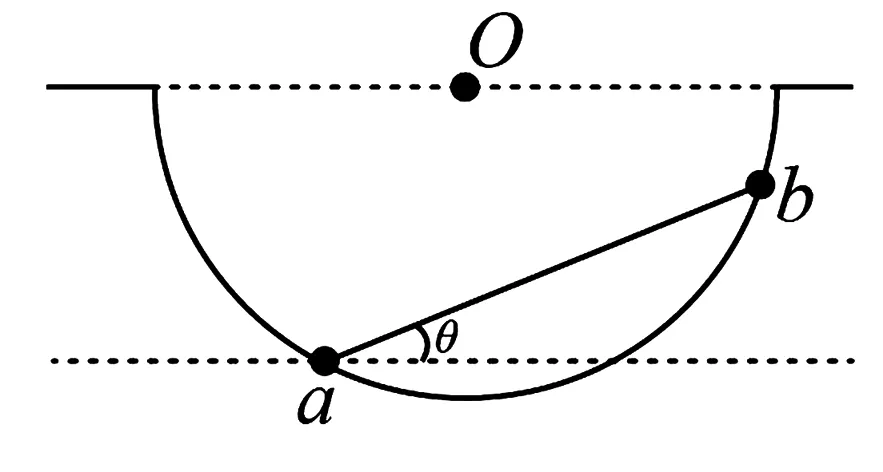
图4 例1题图

A．45° B．30° C．22.5° D．15°

答案:D

详解(1)常规解法一:由题目中的数据可以得出,abO三点组成一个等腰直角三角形,所以两底角都为45°．对两球进行受力分析,由于球面光滑,所以两球都只受到3个力,如图5所示:重力、球面的支持力、刚性细杆的弹力;由于是刚性细杆,所以刚性细杆对两球的弹力均沿着杆方向,且对两球的弹力大小相等;两球处于平衡状态,两球受到的合力都为零,两球受到的三个力都组成一个封闭的力的矢量三角形．

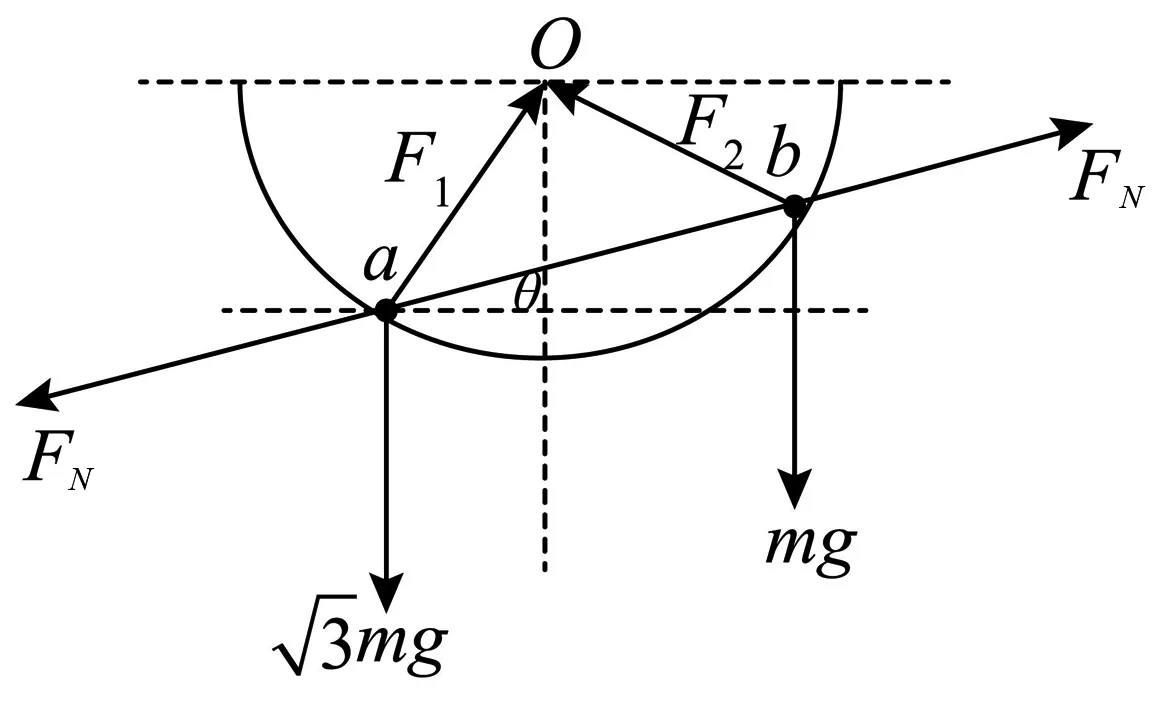
图5 受力分析图

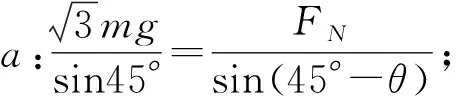
(2)杠杆法:将a、b两球及刚性细杆看成一个整体并取圆心O为支点,整体受力如图6所示.

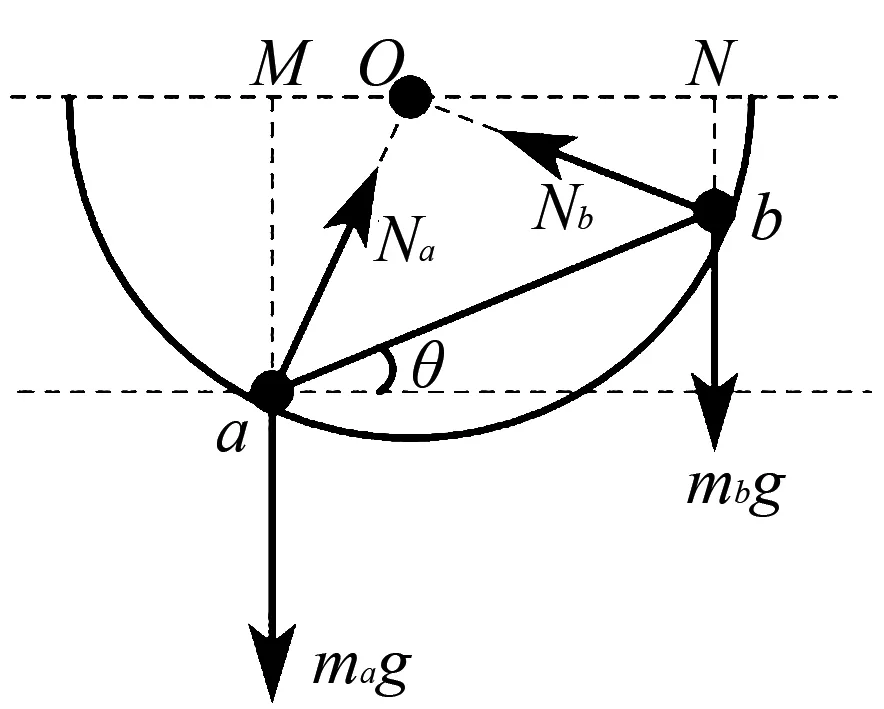
图6 杠杆法

由几何关系可知

∠Oab=∠Oba=45°

由于Na、Nb两个弹力的方向过所选支点,则两个弹力的力距为0,则由“杠杆法”可得

mag·OM=mbg·ON

由几可关系可得

OM=Rcos(45°+θ)、ON=Rsin(45°+θ)

联立可得

解得θ=15°

故选D.

例2(2023·全国·高三专题练习)如图7所示,三根长度均为L的轻绳分别连接于C、D两点,A、B两端被悬挂在水平天花板上,相距2L,现在C点上悬挂一个质量为m的重物,为使CD绳保持水平,在D点上可施加力的取值可能为( ).

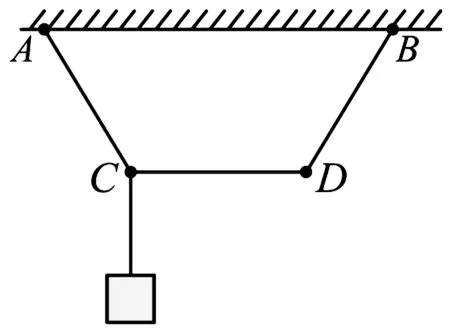
图7 例2题图

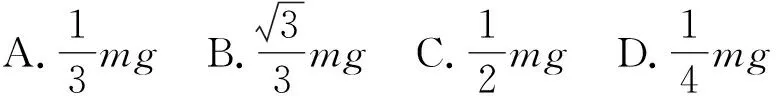
答案:BC

详解(1)常规解法:依题得,要想CD水平,则各绳都要紧绷,则AC与水平方向的夹角为60°,结点C受力平衡,则受力分析如图8所示.

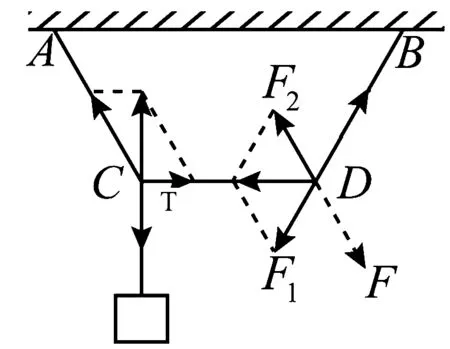
图8 受力分析图

因此CD的拉力为T=mgtan30°

D点受绳子拉力大小等于T,方向向左.要使CD水平,则D点两绳的拉力与外界的力的合力为零,则绳子对D点的拉力可分解为沿BD绳的F1以及另一分力F2.

由几何关系可知,当F2与BD垂直时,F2最小,而F2的大小即为拉力大小,因此有

故BC正确,AD错误.

故选BC.

(2)“杠杆法”取三根轻绳为整体且取O点为支点[3],受力分析如图9所示

图9 杠杆法

由杠杆平衡方程可得mgLsin30°=FLsinα

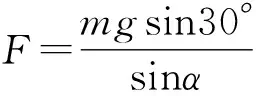
故选BC.