一种水侵气藏动态储量和水侵量计算新方法
岳世俊,刘应如,项燚伟,王玉林,陈汾君,郑长龙,景紫岩,张婷静
(1.中国石油勘探开发研究院西北分院,兰州 730020;2.中国石油青海油田公司勘探开发研究院,甘肃敦煌 736200)
0 引言
水驱气田开发在我国油藏开发中占有重要地位,水侵动态的研究对气藏的高效合理开发具有重要意义[1]。物质平衡方程作为油气藏动态研究的重要方法,在动态储量和水侵量计算中发挥着重要作用[2-4]。对于具有天然水体的气藏,开发过程中随着气藏压力的下降,外围天然水体会侵入气藏,用物质平衡方程来研究该类问题时会出现动态储量和水侵量2 个变量,需要结合其他条件才能求解。目前针对气藏动态储量和水侵量的计算方法较多,常用的动态储量计算方法是采用定容气藏物质平衡方程直接求解,该方法是基于气藏开发初期生产状态,设定水侵量极小,可以忽略,但开发初期生产数据稳定性较差,不可避免会带来一定误差[5-7];对于水侵量的计算,中外学者做了大量研究,其中最为经典的计算方法是Van Everdingen,Hurst 和Fetkovich的水侵量计算模型[8-11],但是其假设过于理想化,计算也繁杂[12-14],实用性有限。
以水驱气藏的物质平衡方程为基础,将井口的生产数据通过体积系数折算为井底数据,计算井下分流率;根据实际气相、水相相对渗透率曲线回归得出井底分流率和出口端含水饱和度的关系,计算出口端含水饱和度;通过均质径向理论模型,建立出口端含水饱和度与地层平均含水饱和度的关系,通过存水体积系数建立平均含水饱和度与气藏动态储量和水侵量的联系,实现动态地质储量和水侵量的计算,以期为水侵气藏的合理开发提供指导。
1 物质平衡理论
根据水驱气藏的物质平衡理论,在开采过程中,储层孔隙体积随着地层压力的下降而下降,束缚水膨胀,外围天然水体侵入地层,造成气体孔隙体积发生变化[15-18]。
式中:Gp,Wp和We分别为累产气量、累产水量和外围天然水体水侵量,m3;G为气藏原始地质储量,m3;Bg和Bw分别为当前压力下气体和水的体积系数;Bgi为原始气体体积系数;Cf和Cw分别为储层岩石和地层水的压缩系数,MPa-1;Swi为地层原始含水饱和度,%;ΔP为地层压力降,MPa。
气体的压缩系数远大于储层岩石和地层水的压缩系数,故可以忽略储层孔隙体积的下降和束缚水膨胀体积,将式(1)简化为
式(2)中含有动态地质储量G和水侵量We这2个未知量,仅凭该式无法求解,整理变形得
根据真实气体状态方程[19],有:
式中:Pi,Psc和P分别为原始地层、标准状况下和当前的地层压力,MPa;Ti,Tsc和T分别为原始地层、标准状况下和当前的地层温度,K;Zi,Zsc和Z分别为原始地层条件下、标准状况下和当前压力下的天然气偏差因子。
将式(4)和式(5)代入式(3),整理得
ω也可表示为气藏原始含气区平均含水饱和度变化值[20],即
确定了气藏平均含水饱和度,可由式(7)计算气藏动态地质储量,由式(8)计算存水体积系数,进而计算出水侵量。
2 计算方法
气藏平均含水饱和度的计算是应用物质平衡方程确定动态地质储量和水侵量的关键[21]。在油水两相渗流中,出口端含水饱和度与地层平均含水饱和度的关系可以用welge 方程加以描述[22-24],但是针对气水两相渗流的研究相对较少,通常直接用出口端含水饱和度代替地层平均含水饱和度,这样会造成较大的误差[25-26]。本文以均质径向地层为例,推导边水气藏开采过程中地层平均含水饱和度与出口端含水饱和度的关系。
首先利用经典的分流理论计算出口端含水饱和度。在计算油水两相分流关系时,井口油与水的产量比可以直接抵消生产压差项,而气水两相渗流相对复杂,井口气和水的产量比不能直接抵消生产压差项,但将井口产气量折算到地层条件下,采用井下流量计算井底分流关系,则可以避免该问题。
当地层倾角较小时,可忽略地层重力;当储层的物性较好时,可忽略气、水的毛管力,因此,可以认为气体渗流遵循达西定律:
式中:Qg和Qw分别为井下气体和水的产量,m3/d;K为储层岩石的绝对渗透率,mD;Krg和Krw分别为气相和水相相对渗透率;μg和μw分别为气相黏度和水相黏度,mPa·s;rw为井半径,m;h为地层厚度,m;r为径向距离,m。
因此,可采取类似油水两相的处理方法[27-28],根据工区实际的气相和水相相对渗透率曲线,得出井底分流率和出口端含水饱和度的关系:
式中:Sw为出口端含水饱和度,%。
通过折算到井底的产量数据,可以得出分流率,从而计算得到出口端含水饱和度。
计算地层水侵后的平均含水饱和度时,假设井口位于圆形均质地层的中心,地层外围连接边水,地层半径为R,生产时边水由圆形地层周边向圆中心侵入(图1)。
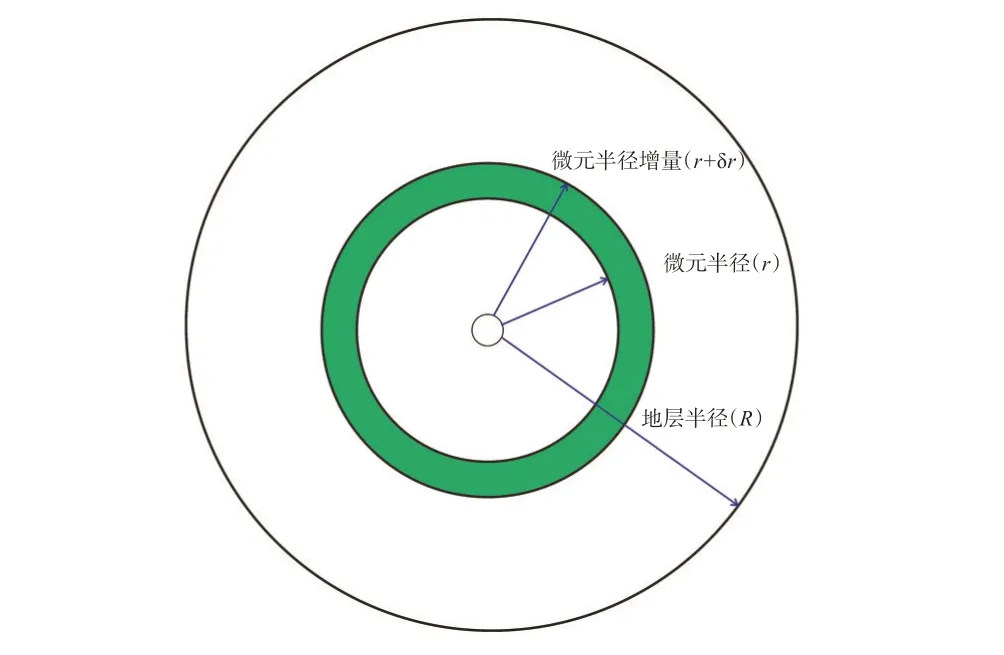
图1 边水气藏径向地层微元体平面示意图Fig.1 Sketch map showing radial formation differential element of a gas reservoir with edge water
根据微元体质量守恒关系,净流入微元体内水质量等于微元体水质量变化量,有:
假设水的密度保持不变,式(13)变形整理可得
式中:t为生产时间,s;ρw为水密度,g/cm3;φ为孔隙度,%。
总体积流量Qt=Qw+Qg,则有
假定总体积流量在不同位置时都相等,将式(15)代入式(14),可得
式(16)用链式求导法则,可改写成
对式(17)采用特征线法求解,有
式(18)自外边界向水侵前缘,分离变量积分,有
计算整理,可得
边水侵入圆形地层中心,即井点,将式(22)和式(23)代入式(21),可得
对式(21)微分,即
将式(24)和式(25)代入式(26),可得
对上式分部积分,整理可得
综上所述,采用物质平衡方程求取水驱气藏动态地质储量和水侵量的过程可分为4 个步骤:①根据实际气相、水相相对渗透率曲线回归得出井底分流率和出口端含水饱和度的关系[式(12)];②将井口气、水产量数据通过体积系数折算为井底产量,计算井下分流率;③根据井下分流率,由式(12)计算出口端的含水饱和度与含水率对含水饱和度的导数,计算地层外边界处含水率对含水饱和度的导数,代入式(28),计算地层平均含水饱和度;④根据地层平均含水饱和度,由式(8)计算存水体积系数,并代入式(7)计算动态地质储量,再代入式(6)计算累计水侵量。
3 实际应用效果
柴达木盆地台南气田处于新生代晚期形成的第四系湖相大型沉积坳陷生气区内,为一近东西向的完整潜伏背斜,无断层发育,沉积微相主要为砂坝、砂滩和泥坪,储层岩性主要为含泥粉砂岩,其次为粉砂岩和泥质粉砂岩。该气田天然气类型为干气,组分以甲烷为主,气体密度小,平均相对密度为0.56,拟临界压力高,拟临界温度低。气、水关系分析表明储层横向连通性好,岩性尖灭现象少,气藏为边水所环绕(图2)。

图2 柴达木盆地台南气田第四系涩北组6 号小层顶面构造Fig.2 Top surface structure of the sixth layer of Quaternary Sebei Formation in Tainan gas field,Qaidam Basin
台南气田第四系涩北组6 号小层为主力产气段,平均孔隙度为23%,平均渗透率为32 mD。于2005 年12 月投产,目前区内生产井59 口,截至2022 年3 月,平均日产气量为37×104m3,平均日产水量为572 m3,水气比为15 m3/104m3,累产气量67.4×108m3,累产水量127×104m3,属于典型的强水侵边水气藏。
根据实际相对渗透率曲线(图3),可以拟合出关系式:

图3 柴达木盆地台南气田第四系涩北组6 号小层气相相对渗透率(Krg)、水相相对渗透率(Krw)和分流率曲线(fw)Fig.3 Relative permeability of gas phase and water phase and fractional flow curve of the sixth layer of Quaternary Sebei Formation in Tainan gas field,Qaidam Basin
式(29)的相关系数高,说明相对渗透率比值的对数与含水饱和度的相关性好,结合式(11),整理得
对式(30)求导可得
代入实际生产动态数据(表1),按步骤②和③,可计算出不同时间段地层平均含水饱和度。
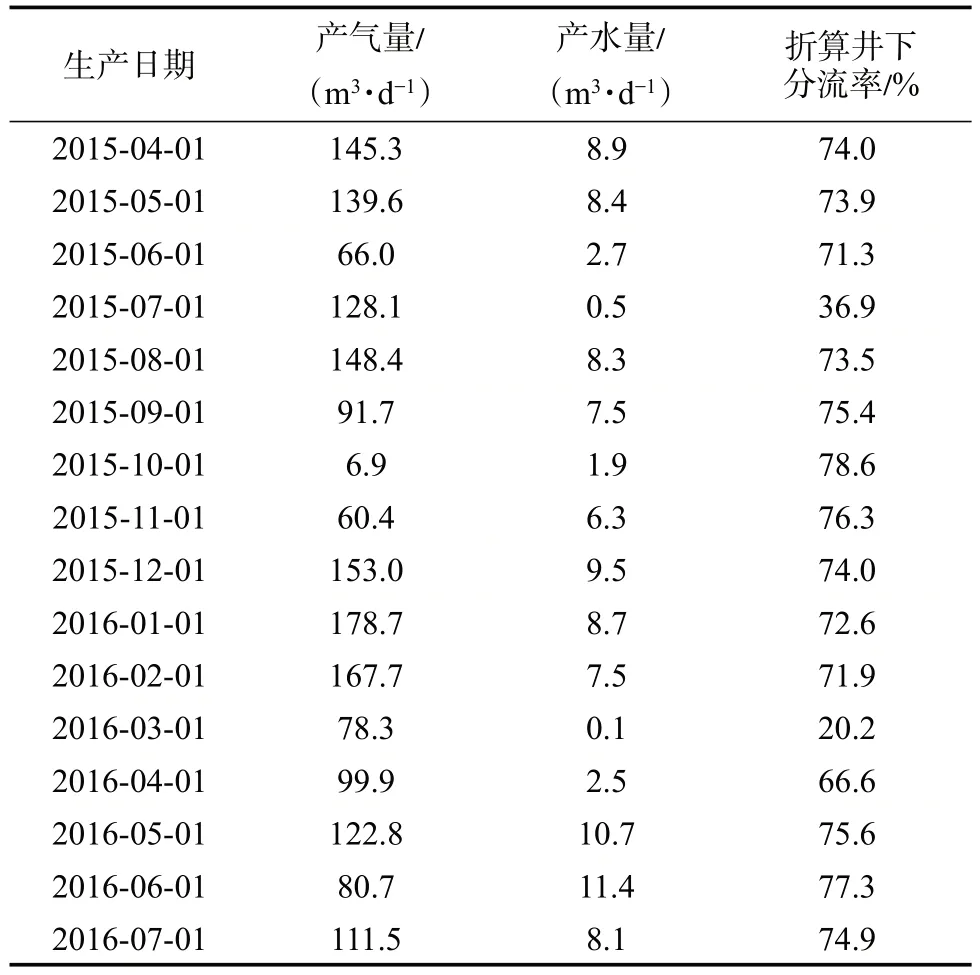
表1 柴达木盆地台南气田产气井部分时间段生产动态数据统计Table 1 The production dynamic data for part time in Tainan gas field,Qaidam Basin
对地层平均含水饱和度与出口端含水饱和度进行拟合,二者具有较好的线性关系(图4),这与其他研究方法,如流管法的研究结果基本一致[29]。
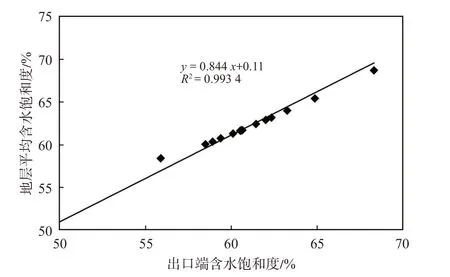
图4 柴达木盆地台南气田产气井部分时间段地层平均含水饱和度与出口端含水饱和度交会图Fig.4 Cross plot of formation average water saturation and exit-end water saturation for part time in Tainan gas field,Qaidam Basin
3.1 视地质储量法验证动态地质储量计算结果
完成地层平均含水饱和度计算之后,就可计算出该区不同时间段的动态地质储量,并与实际应用效果较好的视地质储量法进行对比。根据工程意义,采用视地质储量法计算得出的曲线初期水侵量趋于0 时的视地质储量即为动态地质储量;本文方法则需当生产达到稳定或拟稳定状态且压力降落波及到工区边界时,才能较真实地体现全工区动态地质储量,需参考中后期较为稳定阶段的动态地质储量值。研究区视地质储量曲线初期阶段的动态地质储量为80.9×108m3,采用本文方法计算的中后期稳定阶段的动态地质储量为80.1×108m3(表2,图5),二者相差0.8×108m3,误差为1%。

表2 柴达木盆地台南气田第四系涩北组6 号小层视地质储量与本文方法计算动态地质储量对比Table 2 Comparison of dynamic geological reserves calculated by apparent geological reserves method and the method presented in this paper of the sixth layer of Quaternary Sebei Formation in Tainan gas field,Qaidam Basin

图5 柴达木盆地台南气田第四系涩北组6 号小层2 种方法计算动态地质储量对比Fig.5 Comparison of dynamic geological reserves calculated by the two methods of the sixth layer of Quaternary Sebei Formation in Tainan gas field,Qaidam Basin
3.2 数值模拟验证水侵量计算结果
由于水侵量无法直接进行监测,而数值模拟技术考虑因素相对全面,为了验证本文方法的可靠性,对本算例进行数值模拟验证。
数值模拟(图6)采用斯伦贝谢公司的eclipse100黑油模拟器,通过定亏空控制模式进行压力史拟合,推算出的水体倍数约为13,完成全区及多数单井的产量和压力史拟合后,可输出不同时间的水侵量。

图6 柴达木盆地台南气田第四系涩北组6 号小层数值模拟模型主要属性场Fig.6 Main properties of the numerical model of the sixth layer of Quaternary Sebei Formation in Tainan gas field,Qaidam Basin
将本文方法计算的水侵量与数值模拟法计算的水侵量进行对比(表3,图7),二者具有较好的一致性,其中气井见水后稳定生产时期(2013年以后)的平均误差约为10%,水侵量计算结果在较大程度上受动态储量数值的影响,也再次印证了本文动态储量算法的可靠性。

表3 柴达木盆地台南气田第四系涩北组6 号小层2 种方法计算水侵量对比Table 3 Comparison of water influx calculated by the two methods of the sixth layer of Quaternary Sebei Formation in Tainan gas field,Qaidam Basin

图7 柴达木盆地台南气田第四系涩北组6 号小层2 种方法计算水侵量对比Fig.7 Comparison of water influx calculated by the two methods of the sixth layer of Quaternary Sebei Formation in Tainan gas field,Qaidam Basin
本结论适用于圆形或近圆形地层(如椭圆等)边水气藏,对于其他条件,如一维直线边水驱气藏,也可以用相同方法推导,得出的结论与本文结论一致。
4 结论
本文提供了一种快速、简洁的解析算法,可操作性强,在复杂的水侵气藏动态分析中,有一定实用价值。
(1)地层平均含水饱和度与出口端含水饱和度需加以区分;均质径向地层边水气藏中,地层平均含水饱和度与出口端含水饱和度呈线性正相关。
(2)动态储量的计算结果与时间有关;动态储量计算时应选取开发中后期趋于稳定的数据,此时压力降已经波及到边界,能反映全工区真实的动态储量,计算结果也趋于一致;实例计算表明,利用早期数据计算的结果会偏小。
(3)基于地层平均含水饱和度的物质平衡算法在实例中计算的动态地质储量与视地质储量法计算的动态地质储量,误差为1%;计算的水侵量与数值模拟计算的水侵量,稳定段平均误差约10%,在合理范围内,也再次验证了动态储量计算的准确性;动态地质储量和水侵量计算结果均有较高精度,结果可靠。

