东部地区十省市规模以上工业企业研发投入绩效评价

陈 媛, 王伟华, 王福颖

(济南市科学技术情报研究院, 济南 250001)

1978年,美国运筹学家W.W.Cooper和A.Charnes提出的数据包络分析(data envelopment analysis,DEA)方法[1],主要通过保持决策单元(decision making unit,DMU)的输入或输出不变,借助数学规划将DMU投影到DEA前沿面上,并通过比较决策单元偏离DEA前沿面的程度来评价它们的相对有效性,能有效处理多输入、多输出的复杂系统,可以对多指标投入、多指标产出的同类型部门进行有效的综合评价,本质是一种数学规划模型,在许多领域得到了较为广泛的应用[2]。在运用DEA方法评价科技效率时,无须预先确定投入与产出之间的关系表达式,也无须为各指标赋权重,优势非常明显[3]。虽然DEA方法可以对科技投入产出有效性进行测定,但还是存在一定的局限性,无法反映单个指标的变动对科技投入产出有效性影响的大小[4]。近几年,部分国内学者应用DEA分析方法对企业技术创新效率、研发投入产出效率等开展了研究。例如,胡云红[5]运用DEA-Tobit模型从横向和纵向两个角度测度分析了河北省主要行业规上工业企业的技术创新效率;王佳佳[6]运用两阶段网络EBM模型和Tobit模型对我国38家上市建筑企业整体及分阶段的技术创新效率进行评价;黄兰和常媛[7]以新能源汽车上市公司为研究对象,采用DEA模型分析评价新能源汽车企业的研发效率;吴佳钰[8]运用DEA方法测度了江西省装备制造业研发效率静动态效率;蒋丽丽[9]基于网络SBM模型,构建了建筑企业技术创新效率测算模型,并进行了实际案例应用;黄亚飞[10]采用DEA方法、Malmquist指数分析法对中国各省份的规上工业企业的技术创新效率进行评价,并提出了提高规上工业企业技术创新效率的建议;庞超[11]应用DEA-BCC和DEA-Malmquist模型分别从静态与动态的角度研究陕西省与全国各省份规模以上工业企业R&D投入产出效率情况;罗月[12]采用DEA模型对吉林省工业部门的静态效率进行测算;赵继宗[13]通过主成分分析和数据包络分析相结合的方法对甘肃大中型工业企业2000—2014年技术创新效率的水平进行了评价研究;苏冰杰[14]采用非径向DEA和超效率DEA模型,基于2013—2019年的面板数据对河南省整体及其各地市的研发投入产出现状及绩效进行评价;蒋武林[15]选取运用Input-BCC模型、Bootstrap-DEA模型和改进型SE-DEA模型从静态角度对安徽省规模以上工业企业的生态技术创新效率进行测度。尽管如此,现有文献中尚未见运用DEA方法专门针对中国东部地区10个省份规模以上工业企业的研发投入绩效评价。

《2021年全国科技经费投入统计公报》显示,2021年,全国共投入研究与试验发展(R&D)经费27 956.3亿元,其中企业R&D经费21 504.1亿元,占比为76.9%,企业是研发的主力军,是科技创新的重要力量;R&D经费投入超过千亿元的11个省份有6个在东部地区,R&D经费投入强度超过全国平均水平的6个省份全部都在东部地区。由于企业研发投入产出效率高低直接影响整体创新水平,同时考虑东部地区在企业研发和原始创新方面的重要地位,采用DEA方法开展中国东部地区10个省份规上工业企业研发投入绩效评价。

1 研发投入和研发产出指标

对中国东部地区10个省份规上工业企业的研发投入绩效进行分析评价,侧重于考察研发载体、研发人员、研发经费投入的效率,同时考虑指标数据的可得性,因此选取为“规上工业企业办研发机构数”“规上工业企业R&D人员折合全时当量”“规上工业企业R&D经费内部支出”为研发投入指标;选取“规上工业企业发明专利申请数”“规上工业企业新产品销售收入”为研发产出指标。研发投入产出基础数据如表1所示。

2 DEA模型的构建与分析

2.1 DEA模型的构建

选取中国东部地区10个省份作为决策单元(DMU),分析各省份规上工业企业研发投入产出的DEA有效性,明确其技术效率、投入冗余和产出不足,进而指出改进的方向。选取的评价指标共5个,包括2个产出指标“规上工业企业发明专利申请数”“规上工业企业新产品销售收入”和3个投入指标“规上工业企业办研发机构数”“规上工业企业R&D人员折合全时当量”“规上工业企业R&D经费内部支出”。决策单元数10,评价指标数5,决策单元数是评价指标个数的2倍,可以进行DEA分析。应用DEAP2.1软件进行分析,分析结果自动生成。其中,决策单元数10时,间序列数据设置为1、产出数量为2、投入数量为3,从产出角度衡量技术效率,选用规模报酬不变的CCR模型进行分析。

2.2 各决策单元的技术效率值

表1中每个省份是一个决策单元(DMU),共有10个决策单元,对决策单元构建DEA的CCR模型如下:

(1)

以表1中北京市的数据为例,模型(1)的具体形式为

(2)

由式(2)可求得θ1,即北京市规上工业企业研发投入产出的技术效率。同理可以对其他决策单元列出相应的模型,并求得对应的θj。运行DEAP2.1软件直接得出分析结果,10个省份规上工业企业研发投入产出的技术效率值如表2所示。由表2可知,北京、海南的技术效率值为1,是DEA有效的;其他8个省份的技术效率值小于1,属于非DEA有效的决策单元。

表2 东部地区10个省份规上工业企业研发投入产出技术效率

2.3 非DEA有效单元的分析和改进

2.3.1 研发产出不足的分析和改进

根据分析结果,非DEA有效的8个省份,生产前沿面的目标产出如表3所示。

表3 8个非DEA有效单元生产前沿面的目标产出

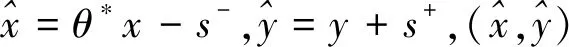
2.3.2 研发投入冗余的分析和改进

根据分析结果,非DEA有效的8个省份,生产前沿面的目标投入如表4所示。

表4 8个非DEA有效单元生产前沿面的目标投入

对非DEA有效单元的研发投入冗余同样通过上述“投影定理”改进。对比表4与表1数据可知,天津规上工业企业在现有研发产出水平下,存在研发投入冗余,规上工业企业办研发机构数应减少201个,R&D人员折合全时当量应减少16 234人年;河北规上工业企业在现有研发产出水平下,研发投入冗余较为显著,规上工业企业办研发机构数应减少1 821个,R&D人员折合全时当量应减少 8 074 人年;上海规上工业企业在现有研发产出水平下,也存在一定程度的研发投入冗余,R&D人员折合全时当量应减少29 602人年,R&D经费内部支出应减少211亿元;江苏规上工业企业在现有研发产出水平下,研发投入冗余较为严重,规上工业企业办研发机构数应减少13 063个,R&D人员折合全时当量应减少253 617人年;浙江规上工业企业在现有研发产出水平下,也存在研发投入冗余,规上工业企业办研发机构数应减少17 974个,R&D人员折合全时当量应减少271 753人年;福建规上工业企业在现有研发产出水平下,也存在研发投入冗余,规上工业企业办研发机构数应减少466个,R&D人员折合全时当量应减少76 966人年;山东规上工业企业在现有研发产出水平下,研发投入冗余也十分严重,规上工业企业办研发机构数应减少5 703个,R&D人员折合全时当量应减少 142 560 人年;广东规上工业企业在现有研发产出水平下,也存在一定程度的研发投入冗余,规上工业企业办研发机构数应减少19 794个,R&D人员折合全时当量应减少128 870人年。8个非DEA有效单元中,仅上海规上工业企业R&D经费内部支出存在冗余,其他7个非DEA有效单元在现有研发产出水平下,R&D经费内部支出均不存在冗余。这说明,对于绝大多数省份来说,规上工业企业当前R&D经费内部支出已充分发挥作用,持续加大规上工业企业R&D经费内部支出仍然是重中之重。

3 灰关联分析

经过DEA分析得到东部地区10个省份规上工业企业研发投入产出效率,但仍未明确哪个研发投入或产出指标对研发投入产出技术效率的影响最大。因此,采用邓聚龙[16]的灰关联分析法分析确定各投入产出指标相对于技术效率的关联度[17],进而提出有针对性的对策建议。灰色关联分析是灰色系统理论中的一种分析方法,关联度是指两个系统或两个因素间关联性大小的量度,它描述了系统发展过程中,因素间相对变化大小、方向、速度等的相对性。按照灰色关联度计算公式直接代入数据进行计算,对于小样本数据而言,具有计算简单、便于操作等优点。

3.1 计算灰色关联度

将10个省份规上工业企业研发投入产出技术效率值作为参考数列x0,研发投入产出指标数据作为比较数列x1、x2、x3、x4、x5,将参考数列和比较数列都进行初值法标准化处理,结果如表5所示。

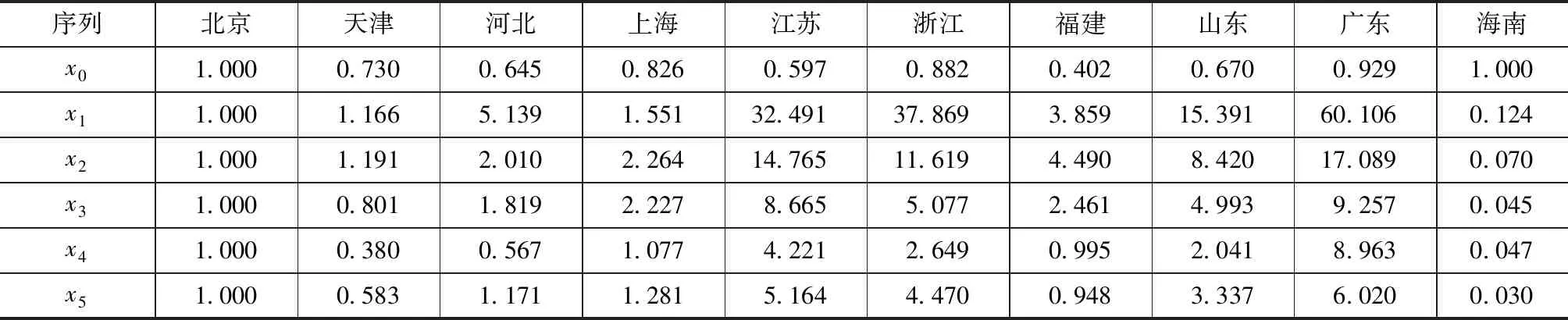
表5 参考数列和比较数列标准化

由表5计算得到,两级最小差Δmin=0,两级最大差Δmax=59.18。

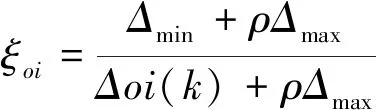
表6 各比较数列与参考数列在各时刻的关联系数

分别计算各比较数列关联系数的平均值,可得各比较数列与参考数列的灰色关联度(表6):r1=0.77,r2=0.87,r3=0.92,r4=0.96,r5=0.95。

3.2 关联度结果分析

由上述计算可知,所选5个研发投入产出指标都与规上工业企业研发投入产出效率存在正向相关关系,其灰色关联度从大到小排序为:发明专利申请数>新产品销售收入>R&D经费内部支出>R&D人员折合全时当量>规上工业企业办研发机构数。由此可见,规上工业企业发明专利申请数与研发投入产出效率的灰色关联度最强,规上工业企业办研发机构数与研发投入产出效率的灰色关联度最弱。

4 结语

采用DEA方法对中国东部地区10个省份规模以上工业企业研发投入绩效进行评价,指标设计和数据选取存在一定局限性。

指标设计方面,投入产出指标较少,在接下来的研究中,需要进一步扩大指标范围,细化指标构成,人员投入指标应考虑研发人员结构,如R&D人员中研究人员、技术人员、辅助人员的比例关系;经费投入指标应考虑研发日常性经费支出和资产性支出的比例关系;产出指标应考虑发表科技论文数、出版科技著作数、认定标准数等。

数据选取方面,研发投入和产出指标的数据年度均为2021年,由于当年的研发投入可能在当年产出,也可能在接下来的若干年内产出,而数据年度的选取直接影响计算结果,因此数据选取也存在局限性。

此外,采用灰关联分析方法分析确定各项研发投入产出指标相对于DEA效率的灰色关联度,由于分辨系数是独立于评价指标之外的一个常数,文中按照常规取分辨系数为0.5,因此灰色关联度计算结果也有一定局限性。在接下来的研究中,需要持续优化研发投入产出指标构成,扩大数据来源,同时加强对灰关联分析中分辨系数选取的研究,建立起规上工业企业研发投入产出的长效分析评价机制。