热辐射和绕组绝缘纸对自然对流下的变压器温度影响

刘演, 彭庆军, 高盛祥, 舒振球

(1.昆明理工大学信息与工程学院, 昆明 650500; 2.南方电网云南电网有限责任公司电力科学研究院, 昆明 650106; 3.昆明理工大学云南省人工智能重点实验室, 昆明 650500)

作为电力系统中最重要和最昂贵的主要电力设备之一,变压器的稳定运行对电力系统的供电可靠性和安全性具有至关重要的意义。其中变压器绝缘老化、破损是导致其故障的一个重要因素[1-2]。变压器的使用寿命和负载能力会受到绝缘纸老化的影响,而温度会加速绝缘纸的老化,因此准确获取变压器内部温度对保障变压器设备的安全高效运行具有重要意义。目前,中外有关变压器温度获取方法主要包括直接测量法[3-4]、经验公式法[5]、热路模型法和数值计算法[6-8],随着计算机性能的提升,现在数值计算法被广泛应用。

针对运用数值计算法来研究油浸式变压器绕组热点温升的问题,主要包括有限差分法、有限体积法和有限元法,而有限元法在处理流体固体交界面的问题上效果较好。国内学者在研究有限元法及其改进算法在变压器流体温度场耦合求解中的应用。文献[9]介绍了一种基于有限元的多物理场耦合法,构建二维模型来分析自冷式变压器绕组的温度分布,但没有考虑油流挡板的影响;文献[10]在运用有限元法计算变压器绕组温度的基础上,还分析了油流挡板和水平油道宽度对变压器绕组温度的影响;文献[11]分析了油浸式变压器在不同的入口油流速度、水平油道宽度、饼式绕组分区数量以及导线匝间绝缘厚度对油道油流流速及绕组温升的影响,对于变压器绕组优化设计具有一定的指导意义;文献[12]分析了油浸纸板分布对绕组热点温升的影响,为进一步讨论换流变压器中理想的油浸纸板位置提供指导;文献[13]用有限元分析了油浸式变压器在极寒条件下的温度场和流场分布;文献[14]分析了匝间绝缘对绕组温升热点的影响,为之后考虑绝缘材料的仿真计算提供了参考。

上述研究首先在针对自然对流散热下的分析计算时,忽略了热辐射和绕组绝缘纸的影响,仿真模型结构的简化会给计算结果带来误差[15];其次在考虑细化结构时,用有限元法求解自然对流散热时难以达到收敛,所以采用有限体积法计算。而有限体积法在计算对流通量和扩散通量过程中,不仅会存在沿控制体积交界面的法向扩散,同时也存在交叉扩散,进而造成求解精度降低。物理中不存在任何形式的隔山打牛,任何源边界、初始条件都有一个作用的空间衰减常数和时间衰减常数。只要这个衰减常数对所关心的区域的影响能忽略不计,就可以认为这个边界和初始条件是可取的或可用的。本文研究先通过设置可以让模型收敛的边界条件,然后再通过一边调试边界条件一边继承之前的收敛值来使得模型最终解趋近于目标值,解决了用有限元求解流体场难以收敛的问题,对运用有限元法计算细致化结构的自然对流问题和自然对流散热形式的变压器设计提供了指导思想。

现以1台型号为SSZ20-63000/110的油浸式变压器为原型,建立包含垫圈、绝缘纸筒、压板、绕组绝缘纸和黑体热辐射的变压器热点温升物理计算模型,并基于有限元仿真,计算在自然对流下变压器绕组的热点和温升以及变压器油的温升,期望仿真计算结果与实际变压器试验值误差较小,绝缘纸和热辐射对变压器绕组的热点和温升有较大影响。

1 计算模型

1.1 控制方程

由于变压器绕组具有对称性,为便于计算,采用二维轴对称模型。在二维稳态轴对称的情况下, 油部分的流体控制方程为

(1)

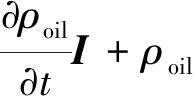
(2)

油、绕组、铁芯部分的热力学方程为

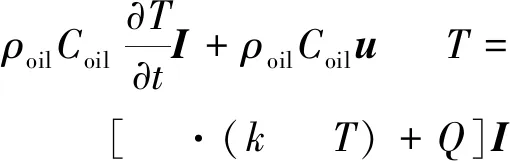
(3)

(4)

式中:Q=QI-Qcon-Qrad;ρoil为导线周围油密度;u为导线周围油流速;p为导线周围油压强;I为单位矢量;μ为油的动力黏度;ρ绕组为导线密度;k为热传导系数;Coil为导线周围油比热容;T为油或绕组的温度;C绕组为导线的比热容;QI为绕组通过电流自身产生的热量;Qcon为绕组对流散热的热量;Qrad为绕组辐射的散热量,且满足斯蒂芬-波尔兹辐射定律。

1.2 物理模型

以一台型号为SSZ20-63000/110的油浸式变压器作为研究对象,由于变压器绕组具有良好的轴对称性,为了降低求解的规模,根据绕组热点温升的对称性建立二维轴对称模型,如图1所示。图1中,低压绕组分为87段;中压绕组分为96段;高压绕组分为88段。

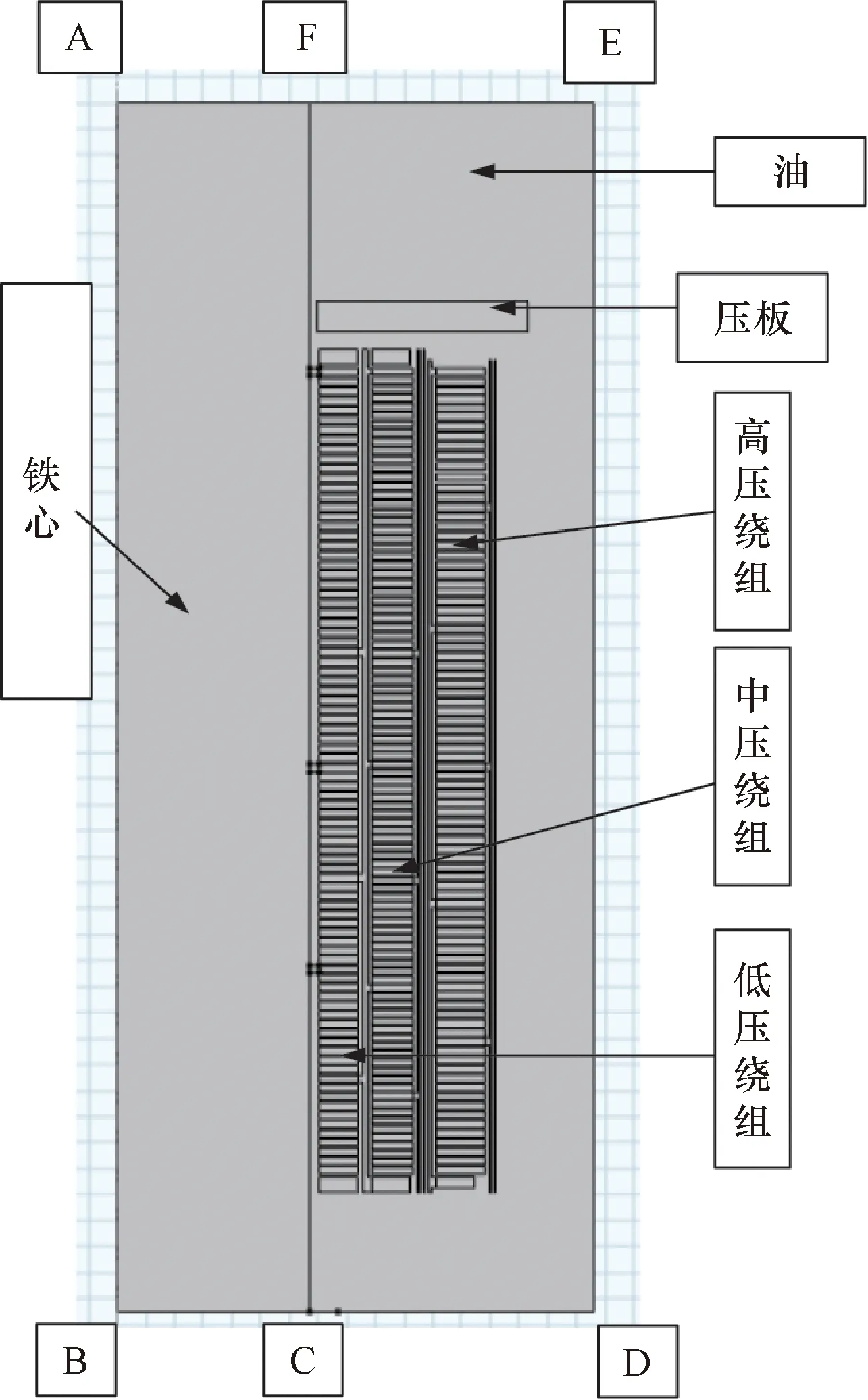
AB为对称轴;ABCF为铁心部分

1.3 热源、材料参数及边界条件

根据变压器算单中提供的高压110 kV、中压38.5 kV的组合电压下,各损耗如表1所示。

表1 变压器各部分损耗

根据偏差比为3.26%,二维轴对称模型下的面积占比计算出铁心热源为4 880.1 W、中压绕组热源为42 129 W、高压绕组热源为56 754 W。

由图1可知,绕组温升计算结构包括变压器油、铁心、绕组、绝缘纸和若干种材料,这些材料与流场及温度场计算有关的物性参数如表2所示[16]。其中,变压器油的物性参数受温度的影响比较大,其为温度的函数,其他固体材料的物性参数受温度影响较小,假定其为常数。

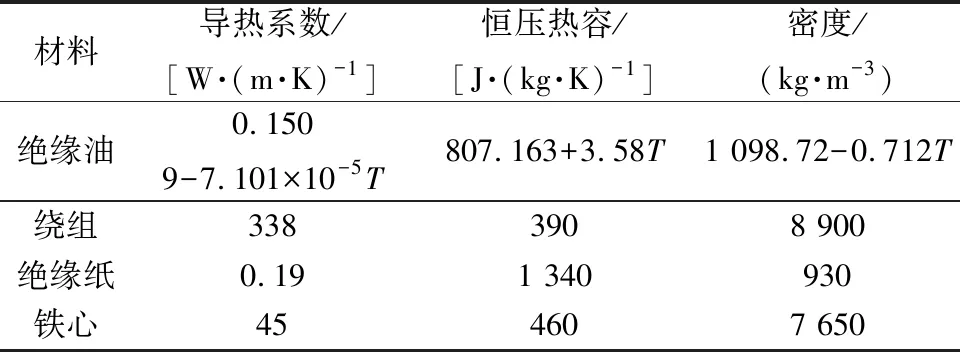
表2 变压器物性参数

因为有限元的方法能够自适应的满足固体和流体交界面上热流密度的连续性,从而不用单独处理交界面。图 1 所示为三相三柱油浸式变压器的一相二维轴对称模型,其中CD、DE、EF为流体边界,所以都为滑移边界条件,即满足如下方程。

un=0

(5)

Kn-(Knn)n=0

(6)

式中:n为速度法向矢量;Kn为边界上的平均黏性应力。

同时,CD、DE、EF设置为热通量边界条件,即满足

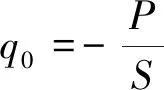
(7)

式(7)中:q0为广义向内热通量;P为铁心和绕组的总功率;S为除去铁心后模型旋转一周的表面积。油流与固体之间为无滑移壁面边界条件,即满足边界速度为0。

油流入口和出口为开放边界条件,即满足

Phydro=ρoilg(r-rref)

(8)

(-pI+Kn)n=- (f0+Phydro)n

(9)

式中:f0为正应力;Phydro为相对压力;g为重力加速度;r-rref为高度差。

1.4 网格参数

有限元求解过程中对求解域进行合理的网格划分是正确求解的关键,尤其是在那些物理量梯度较大的区域,网格的划分是比较重要的[15, 17]。对各区域进行了合理的加密,对铁心和绕组采用不同精度的结构化网格剖分,对其余部分采用自由三角形网格剖分,如图2所示。

图2 单元网格质量统计

网格单元质量是衡量网格好坏的重要参数,其中最好为1,而当单元质量小于0.1时其求解的结果难以收敛。根据图2可以看出,所划分的单元质量都是远大于0.1。为直观地表述出文中所采用的网格情况,给出求解域网格参数如表3所示,根据表3可以看出,本文研究采用的网格单元平均质量达到0.801 9。

表3 网格参数统计

1.5 计算平台

近几年随着各种有限元软件的发展,在求解变压器绕组热点温升时可供选择的代码也增多,其中以处理多物理场耦合而闻名的有限元软件Comsol Multiphysics®6.0在变压器多物理场耦合计算中已得到了广泛的应用,且取得了很大成功[10-11, 13, 18],因此,本文研究的计算实验将基于该软件平台。

2 仿真模型可靠性分析

实例性的,根据额定容量为63 000 kVA的三相三柱油浸式变压器绕组参数如表4所示,此外铁心柱直径为670 mm,铁心窗高为1 780 mm,压板内径116 mm,压板外径238 mm,压板厚度174 mm。利用有限元软件构建与所述目标变压器比例为1∶1的初始仿真模型:在铁心、低压绕组、中压绕组和高压绕组的边缘处采用极端细化网格剖分,其他区域采用标准细化网格剖分,网格剖分总单元数为77 063,得到所述目标变压器的仿真耦合计算模型。

表4 实际变压器绕组参数

结合在环境温度为297.15 K的条件下,对该变压器进行现场实验,得到传统变压器设计的5个必需计算指标(油平均温升、顶层油温平均温升,低、中、高压绕组平均温升)。把仿真计算结果与这5个算单指标进行误差计算,对这5个指标对应的部件都采用四阶积分的方法求解平均值,仿真值与试验值的误差如表5所示,各指标的温升分布如柱状图如图3所示。

表5 仿真值与试验值对比

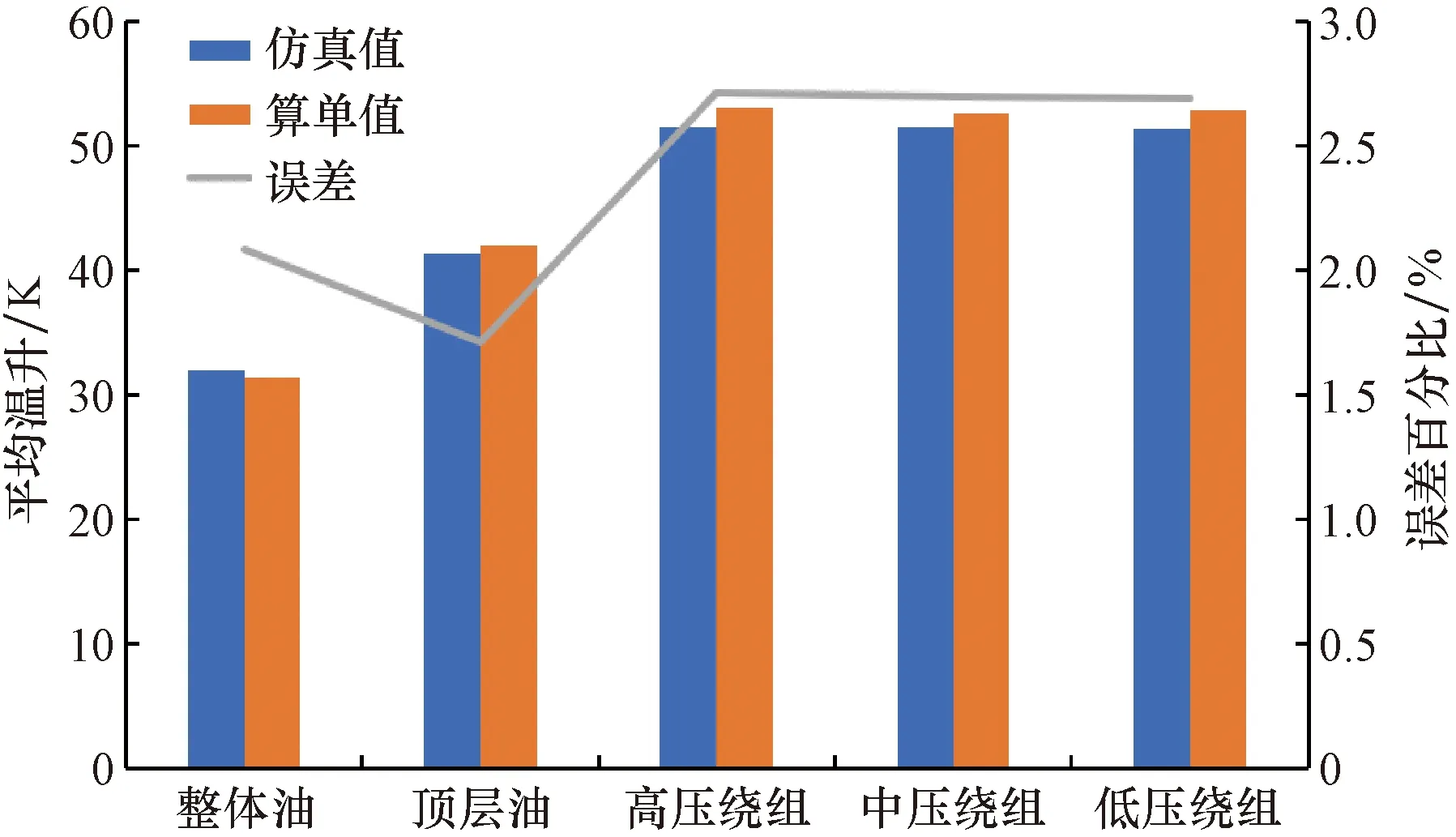
图3 变压器5项温升计算指标

表5中的低、中、高压绕组的平均温升值分别为51.41、51.45、51.56 K,变压器油的平均温升和顶层油温平均温升分别为31.94、41.27 K。绕组平均温升偏差达到不超过3%、油平均温升偏差达到不超过3%、顶层油温平均温升不超过5%的工程要求,所以本文采用的仿真模型是可行的,接下来可以进行定性分析。

3 辐射和绝缘对变压器温度的影响

3.1 对绕组热点大小和位置分布的影响

在变压器绕组的温度仿真计算中往往忽略掉热辐射的影响,但是热辐射是一切物体的固有属性,自然界中的一切物体都在不停地向周围发射电磁波。这些电磁波到达其他物体后将根据波长的大小产生不同的效应,有的能提高物体的温度。

通过对绕组添加表层热源,该表层热源会对周围环境产生热辐射,两个物质通过热辐射传热满足

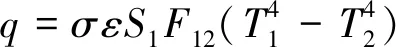
(10)

式(10)中:σ为斯特藩-玻尔兹曼常数,其值为5.670×10-8W/(m2·K4);ε为辐射率;S1为热辐射物体的表面积;F12为辐射面到被辐射面的形状系数;T1和T2分别为热辐射物体与被辐射物体的温度。

饼式变压器的结构中绕组由多个线饼构成,线饼外由一层绝缘纸包裹。内绝缘问题不仅是造成变压器故障的主要原因之一,而且也是长期以来制约变压器电压等级和容量提高的一个重要因素。变压器绕组和铁芯为金属材料,200～300 ℃下也可以保持其机械强度;变压器油也不会在低于140 ℃左右的温度下发生明显劣化进而造成故障;但变压器的油纸绝缘系统却对温度非常敏感,忽略匝间绝缘在建模和计算时带来极大简化,但是这样处理难以反映真实的热源情况。匝间绝缘作为变压器热源的覆盖物,对绕组的热点分布和温升影响不可小视。

对线饼上添加一层薄层结构,物性参数设置为表2中的绝缘纸,图4为各个影响因素下的变压器温度分布。

图4 不同因素下的变压器温度场分布

从图4中可以看出,原本绕组的热点温度为348 K,单独考虑热辐射影响的绕组热点温度为350 K,升高了2 K;单独考虑绝缘层的绕组热点温度为361 K,比原本的热点温度上升了13 K;而同时考虑热辐射和绝缘层影响的绕组热点温度为366 K,比原本的热点温度上升了18 K。为观察各因素对热点位置分布的影响,本文研究取中压绕组和高压绕组上的温度进行分析,如图5所示。

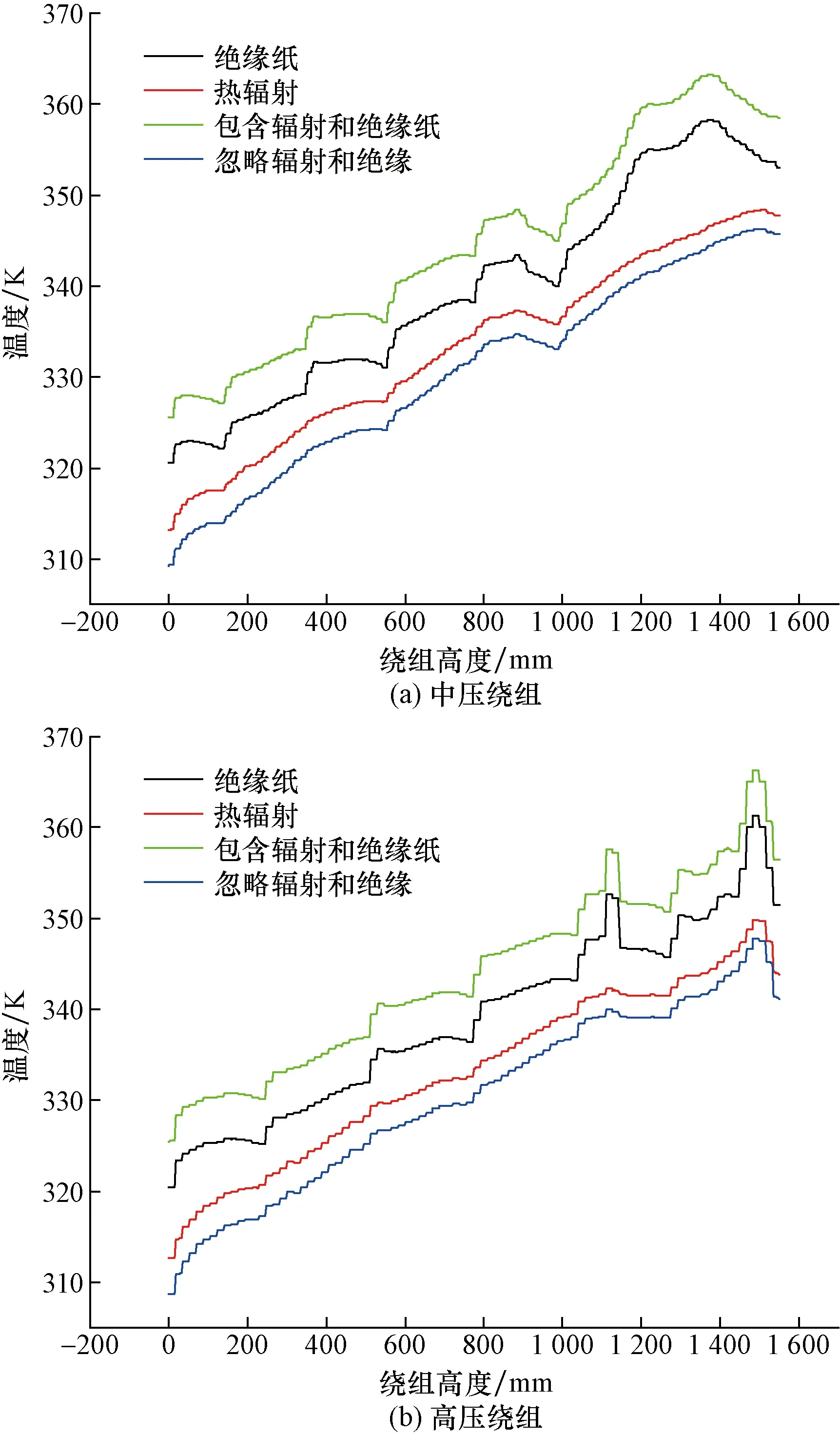
图5 不同因素下的绕组温度分布

从图5可以看出,热辐射对绕组热点位置的分布没有影响。而绝缘纸出现了局部温度大幅上升的现象,这正是由于绕组上层分区的油道较大,利于散热,其余油道的位置较窄,这是由于变压器绕组各个分区的衔接处油道宽度不同导致的,由表2中绝缘纸的导热系数为0.19,导热性极低,绝缘纸会使得绕组的温度在油道窄的位置大幅度上升。所以在设计变压器时,应适度调整绕组分区衔接处的油道宽度。

3.2 对绕组和变压器油温升的影响

工程中往往用传感器对变压器顶层的油温进行测量,然后以热模拟的方法来推测出变压器绕组的热点温度[19]。实际中的热点温升计算都要考虑到热辐射和绝缘层的影响。采用四阶积分计算的顶油温度平均温升与工程中从变压器顶层测得的变压器油温误差仅为1.71%,远远小于工程中要求的5%。

为分析热辐射和线饼绝缘层对自然对流下变压器绕组温升的影响,用控制变量法分别计算了单独考虑热辐射、绝缘纸及其同时考虑热辐射和绝缘纸影响的变压器绕组的温升,温升对比结果如图6所示。

图6 各因素下的平均温升分布

从图6中可以看出,热辐射和绝缘纸对油的平均温升影响较小,大约会使油的平均温升上升2 K。单独考虑绝缘纸和同时考虑辐射和绝缘纸时的影响效果基本相同,热辐射对其余指标影响较小,温升主要还是受绝缘纸的影响。

4 结论

基于有限元方法开展对110 kV油浸式变压器在自然对流散热时,热辐射和绕组绝缘纸对变压器绕组的热点和温升的研究分析,通过对63 000 kVA油浸式变压器的研究,可得出如下结论。

(1)绕组绝缘纸会使变压器绕组的热点值大幅增加;单独考虑热辐射时,绕组的热点值会小幅增加,基本可以忽略;但是当同时考虑热辐射和绝缘纸时,热点值会比单独考虑绝缘纸时的高5 K,此时不能忽略热辐射的影响。

(2)热辐射不会影响热点的位置分布,而绕组绝缘纸会使热点位置发生下移,并且会使油道窄的位置温度发生大幅上升,因此在设计变压器时,应在分区时给予足够的油道宽度。

(3)热辐射和绝缘纸对油的平均温升影响较小,大约会使油的平均温升上升2 K。单独考虑绝缘纸和同时考虑辐射和绝缘纸时的影响效果基本相同,热辐射对其余指标影响较小,温升主要是受绝缘纸的影响。

(4)在实际工程计算中,当只计算温升值时,热辐射可以忽略,但是在计算热点值时,热辐射不能忽略,否则误差较大。无论进行何种计算,都不能忽略绝缘纸的影响。