基于粒子群优化的升降机驱动装置控制策略
卢宁, 刘雪岩
(北京建筑大学机电与车辆工程学院, 北京 100044)
施工升降机[1]作为高层建筑施工的基础设备,其运行过程的稳定性和快速性大大影响施工工作的生产效率与安全性,因此,改进施工升降机控制系统对施工生产具有巨大的实用意义。
施工升降机驱动装置是由3台三相异步电机驱动,通过传动装置实现吊笼升降动作。在其传动过程中,齿轮、齿条、蜗轮、蜗杆存在齿侧间隙和啮合误差以及摩擦等非线性因素,影响了传动的平稳性和精度[2]。在工业控制领域中常采用常规比例、积分和微分(proportional integral derivative,PID)控制方法对联动装置进行控制,而由于靠人工经验调节参数,很难在非线性系统控制方面得到很好的控制效果[3-4]。为实现对系统精确控制,设计一种合理控制策略十分必要。
目前,对于非线性系统难以建立准确数学模型的问题,吴炜等[5]建立基于ADAMS 与Simulink的虚拟仿真平台,对一种重心调节装置控制系统进行联合仿真。莫程凯等[6]通过联合仿真平台对模糊自抗扰的双电机同步驱动电动缸起竖的控制策略进行了研究。同时,神经网络控制[7]、滑模控制[8]算法相比传统PID 算法,针对非线性控制系统大大提高了精确度,可以实现精确控制,但由于运算量过大很难在短时间做出灵敏的反应,难以满足施工升降机驱动装置的实际控制需求。
因此,现设计一种基于粒子群优化的PID控制器[9],利用机电联合仿真平台进行仿真分析,使得PID参数进行实时动态调整,与传统PID控制策略以及模糊PID控制[10]策略进行对比,验证控制方案的合理性。
1 升降机传动系统分析
1.1 机械构成分析
驱动装置包括异步电机、蜗轮蜗杆减速器、圆柱直齿轮、齿条、吊笼、机架等部分。装置由3台三相异步电机输出动力,通过3台减速器将力矩传递给末端驱动齿轮,齿条固定于标准节上,通过齿轮齿条间的啮合实现升降机吊笼完成升降动作[11]。
驱动装置传动示意图如图1所示。
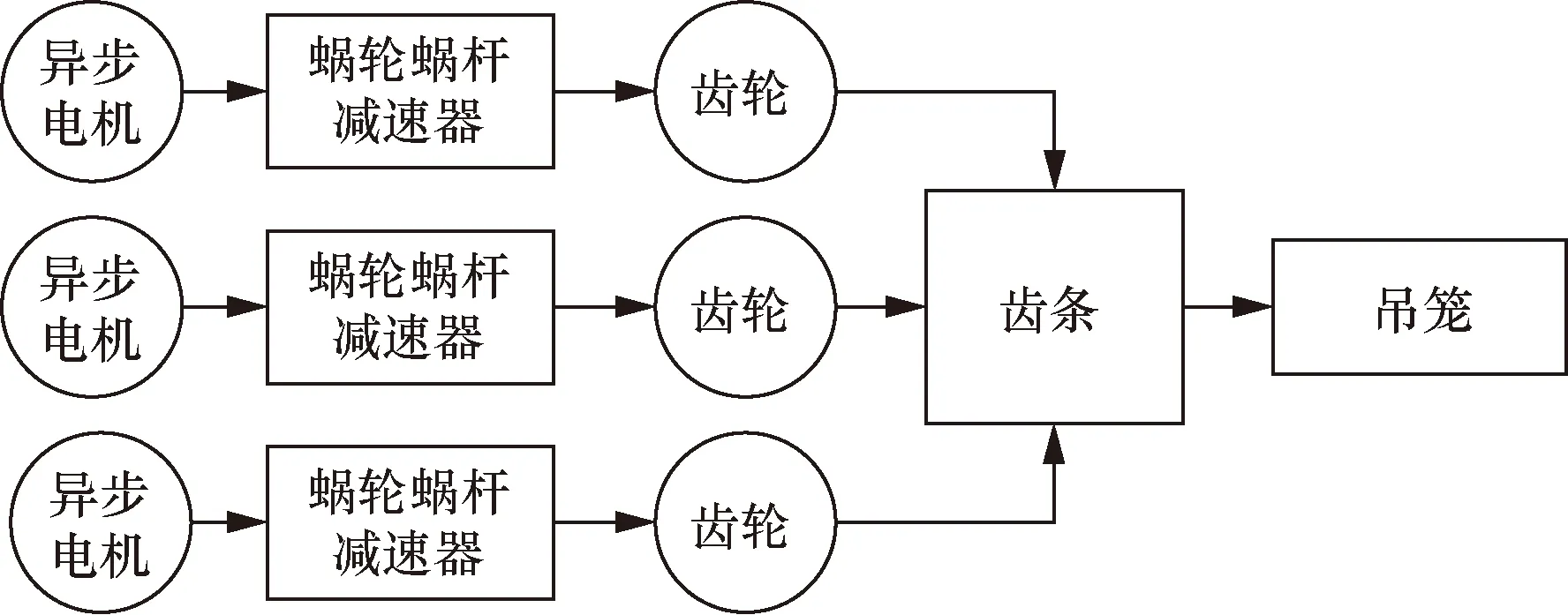
图1 驱动装置传动示意图
1.2 控制系统分析
根据升降机驱动系统分析,确定可编程逻辑控制器(programmable logic controller,PLC)、变频器、编码器为控制系统主要硬件。系统控制流程如图2所示。

图2 控制系统流程图
控制系统控制对象为升降机吊笼,采用PLC为系统控制器。编码器固定于吊笼背板,通过齿轮与齿条啮合,当吊笼运动时带动编码器转动可测得吊笼运行位移。
2 驱动装置系统建模
2.1 矢量控制系统建模
由于三相异步电机的动态数学模型具有高阶、非线性、强耦合的多变量系统的特性,在对其建模中不可简单等效或简化。矢量控制理论发展成熟,在实际工程中通过变频器对异步电机进行矢量控制应用广泛。因此,采用矢量控制的方式在Simulink中对升降机异步电机建立变频调速控制模型,在建立中需忽略空间谐波、磁路饱和、绕组电阻以及铁芯损耗的影响[12]。
三相异步电机按转子磁链定向方式的同步旋转正交坐标系状态方程如下。
电压方程为


(1)
磁链方程为
(2)
转矩方程为
Te=npLm(isMirT-isTirM)
(3)
运动方程为
(4)
式中:usM、usT为定子等效绕组电压;urM、urT为转子等效绕组电压;ωs、ωr为定、转子相对角速度;Rs、Rr为定、转子绕组电阻;ω1为同步旋转角速度;ψsM、ψsT为定子磁链;ψrM、ψrT为转子磁链;Lm为定、转子等效绕组互感;Ls、Lr为定、转子等效绕组自感;isM、isT为定子等效绕组电流;irM、irT为转子等效绕组电流;p为微分算子;Te为电磁转矩;np为极对数;TL为负载转矩;J为等效转动惯量;ω为转子转速。
在建模过程中,转子磁链环节为稳定的惯性环节,采用闭环控制的方式。同时为实现控制系统动态响应更快,采取电流跟随脉冲宽度调制(pulse width modulation,PWM)方式进行电流闭环控制。转速、转矩、以及磁链控制器采用比例积分(proportional integral,PI)控制器。 电机参数如表1所示。
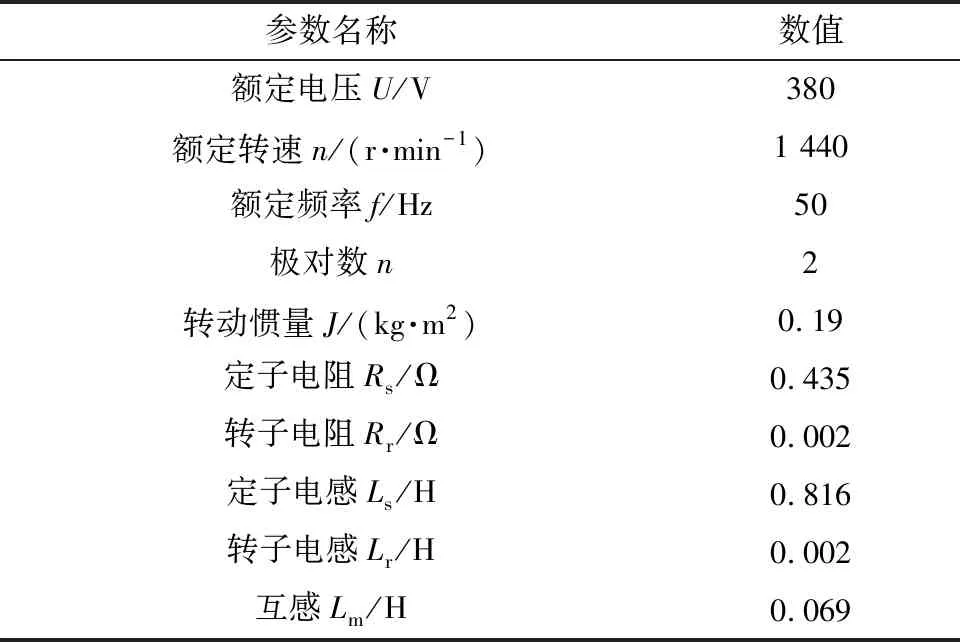
表1 电机参数表
在MATLAB /Simulink 模块中建立的电机仿真模型如图3所示。

Continuous为连续函数模块;[n]为输出转速;Te为电磁转矩;为电磁转矩;ist*为定子电流转矩分量;fcn为函数模块;Phir、phir为转子磁链;ist为电流分量;theta为转角;w为输入转速;d、q为电流分量;a、b、c为电流分量;[A]为输出转速;Tr为电磁时间常数;Iabc为实际电流; Iabc*为电流给定值;pulse为PWM信号;[is_abc]为输出三相电流;-K- 为比例系数;g为PWM信号;A、B、C为电机模块相线
2.2 系统动力学建模
电机输出力矩与减速器减速后输出力矩关系为
(5)
式(5)中:Jm1、Jm2、Jm3为电机的转动惯量;Jr1、Jr2、Jr3为减速器的转动惯量;θ1、θ2、θ3为电机的转动角度;Bm1、Bm2、Bm3为动摩擦因数;M1、M2、M3为减速器的输出力矩;i为减速器的传动比。
减速器输出力矩与经过小齿轮输出力矩关系式为

(6)
式(6)中:Jg1、Jg2、Jg3为齿轮的转动惯量;θg1、θg2、θg3
为齿轮的转动角度;Bg1、Bg2、Bg3为动摩擦因数;TL1、TL2、TL3为负载力矩。
在实际运动过程中,蜗轮蜗杆减速器、齿轮齿条由于存在齿隙或外界因素等特点易导致啮合不平稳,使得传动不均匀,使得齿轮转动速度呈非线性变化。因此,本文研究采用在ADAMS中建立传动机构虚拟样机,使得啮合接触过程更加准确[13]。
首先在SolidWorks软件中建立蜗轮蜗杆减速器、圆柱直齿轮、齿条、吊笼、机架等传动机构的三维模型,保存为parasolid格式后并将其导入ADAMS中,添加齿轮间的接触力以及各部件之间的约束及运动副。约束/运动副设置如表2所示。

表2 约束/运动副设置
在ADAMS中,驱动装置动力学模型以及传动机构局部放大图如图4和图5所示。
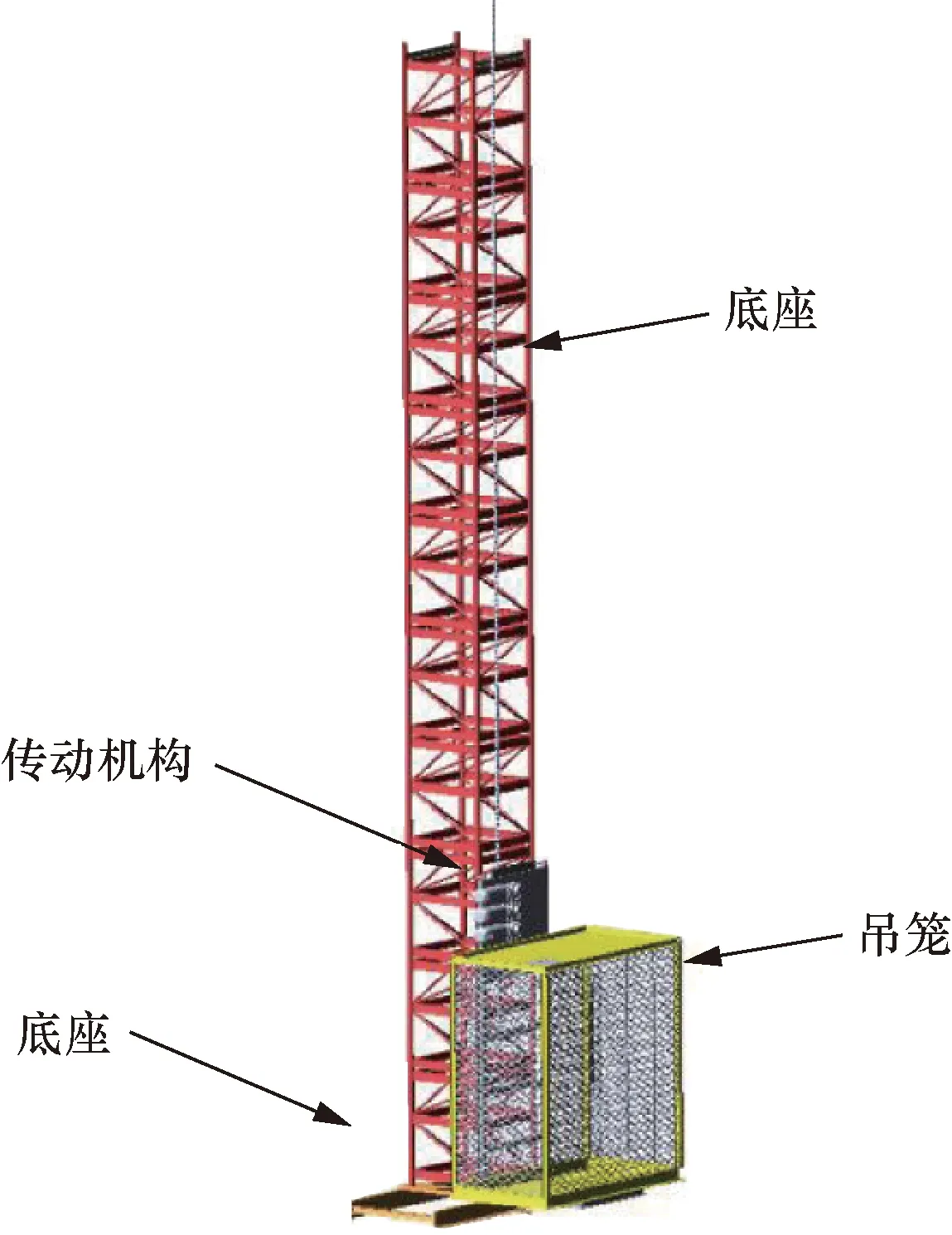
图4 驱动装置动力学模型

图5 传动机构局部放大图
2.3 仿真平台搭建
通过粒子群PID控制算法对吊笼进行位置控制,控制器获取吊笼位移的误差信号进行调节,设置限幅用以模拟PLC模拟量输出信号,驱动器驱动变频电机输出转速ω作为ADAMS中输入状态变量,吊笼运行位移S、负载转矩M为输出接口变量。
利用ADAMS/Contols接口导出为MATLAB接口文件,在MATLAB中运行指令调出ADAMS的Simulink系统模块,将其拖入Simulink中与控制算法连接,设置仿真步长及系统仿真时间后运行联合仿真。联合仿真控制系统如图6所示。

|u|为取绝对值;PID(z)为离散PID模块;-K-为比例系数;为积分环节;w1、w2、w3为输出转速;e1、e2、e3输出误差;w输入转速;TL为负载转矩;[A]为输出转速;TL为负载转矩
3 系统控制器以及同步驱动设计
3.1 粒子群PID控制器设计
粒子群算法[14]是一种基于飞鸟集群活动规律性启发的全局优化算法。算法每个粒子代表一个可能的解向量,从随机解出发,通过迭代寻优寻找个体最优解与全局最优解,同时更新速度和位置来实现全局优化。粒子在搜索空间中的速度和位置为
vi+1=ωvt+c1r1(Pt-xt)+c2r2(Gt-xt)
(7)
xt+1=xt+vt+1
(8)
式中:xt+1、xt为粒子的位置;vi+1、vt为粒子的速度;ω为惯性因子;c1、c2为加速常数;Pt为第t个微粒的最好位置;Gt为群体的最好位置;r1、r2为[0,1]的随机数;Pt为粒子迄今为止搜索到的最优位置。
粒子群算法通过将Simulink控制系统模型中粒子(即Kp、Ki、Kd)与该粒子对应的适应度值建立联系。
优化过程首先产生初始化粒子群或更新后粒子群赋值给PID控制器,并运行Simulink系统模型得到粒子对应的性能指标,然后将指标作为粒子群中粒子的适应度值,通过判断最终结束算法。优化过程示意图如图7所示。

图7 优化过程示意图
PID控制器的参数整定问题实际上为多维函数优化问题,粒子群算法优化过程中适应度作为最优值的反映,其关键在于使优化后控制系统偏差e(t)趋于0,同时具有较快的响应速度与较小的超调量。由于时间乘误差绝对值积分(integral of timed absoluted error,ITAE)性能指标可反映控制系统速度与精度,因此选用其作为控制器整定适应度函数,可表示为

(9)
式(9)中:JITAE为适应度值;t为时间;e为系统控制误差。
3.2 模糊PID控制器设计
模糊控制器PID控制性能以及控制复杂性相对较好,因此得到广泛应用[15]。在MATLAB 中建立模糊控制器,将吊笼的位移的误差量e和误差变化率ec作为输入,乘以一定比率Ke、Kec,通过输出变化量ΔKp、ΔKi、ΔKd实现对传统PID控制器参数进行整定。模糊PID控制结构图如图8所示。

Xi(t)为输入位移;Xf(t)为反馈位移;Xo(t)为输出位移
设定输入和输出变量模糊子集均为{NB(负大),NM(负中),NS(负小), ZO(零),PS(正小),PM(正中),PB(正大) }。e和ec 的基本论域为(-10,10),ΔKp、ΔKi、ΔKd的基本论域分别为(-1,1)。根据隶属度函数特性及其系统特性要求,采用工程上常用的三角形隶属度函数来建立定义好的模糊论域与模糊语言变量之间的关系,根据PID 控制调节经验规律,建立模糊控制规则。模糊规则表如表3所示。

表3 模糊规则表
3.3 同步驱动控制设计
由于升降机驱动装置由多台电机驱动运行,工程实际中常采用变频器一拖三的形式,同步精度低、机械结构易磨损[16],影响升降机运行稳定性。因此基于偏差耦合同步控制结构设计了偏差耦合控制器,将被控电机的实际速度与其他各个电机的实际速度分别作差经过PI控制器,作为各个被控电机的输入补偿,从而驱动3个电机转速一致,达到转速同步。PI速度补偿器结构如图9所示。

ω1、ω2、ω3为电机输入转速;e1为输出误差值
4 控制系统仿真
仿真实验设置传统PID、粒子群优化PID和模糊PID 3种方案,对不同方案的系统响应能力进行对比[17]。
仿真中工程试凑法整定得到PID参数Kp=0.004、Ki=0.000 5、Kd=0.000 1,偏差耦合控制器参数为Kp=2;负载转动惯量Jm=22.776 kg/m-2;摩擦系数Bm=0.01 (N·m·s)/rad;减速器减速比i=16;惯性权重w=0.7;学习因子c1=2,c2=2;维数D=3;粒子群规模为SwarmSize=30;最大迭代次数MaxIter=30,最小适应度值为MinFit=0.1。
粒子群适应度值优化结果和Kp、Ki、Kd优化曲线如图10和图11所示。

图10 适应度值优化结果
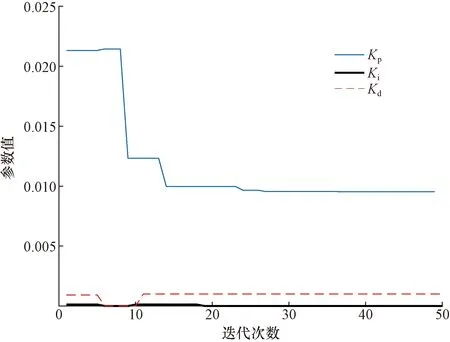
图11 Kp、Ki、Kd优化曲线
粒子群优化后得到的PID参数为Kp=0.009 5、Ki=0、Kd=0.001,迭代次数到达28次时,适应度值趋于稳定,取得最优适应度值为551.8。
设定吊笼运行位移为3 m,在0 s以0.55 m/s速度匀速运行。图12所示为PID、粒子群优化PID和模糊PID对应吊笼位置响应曲线。
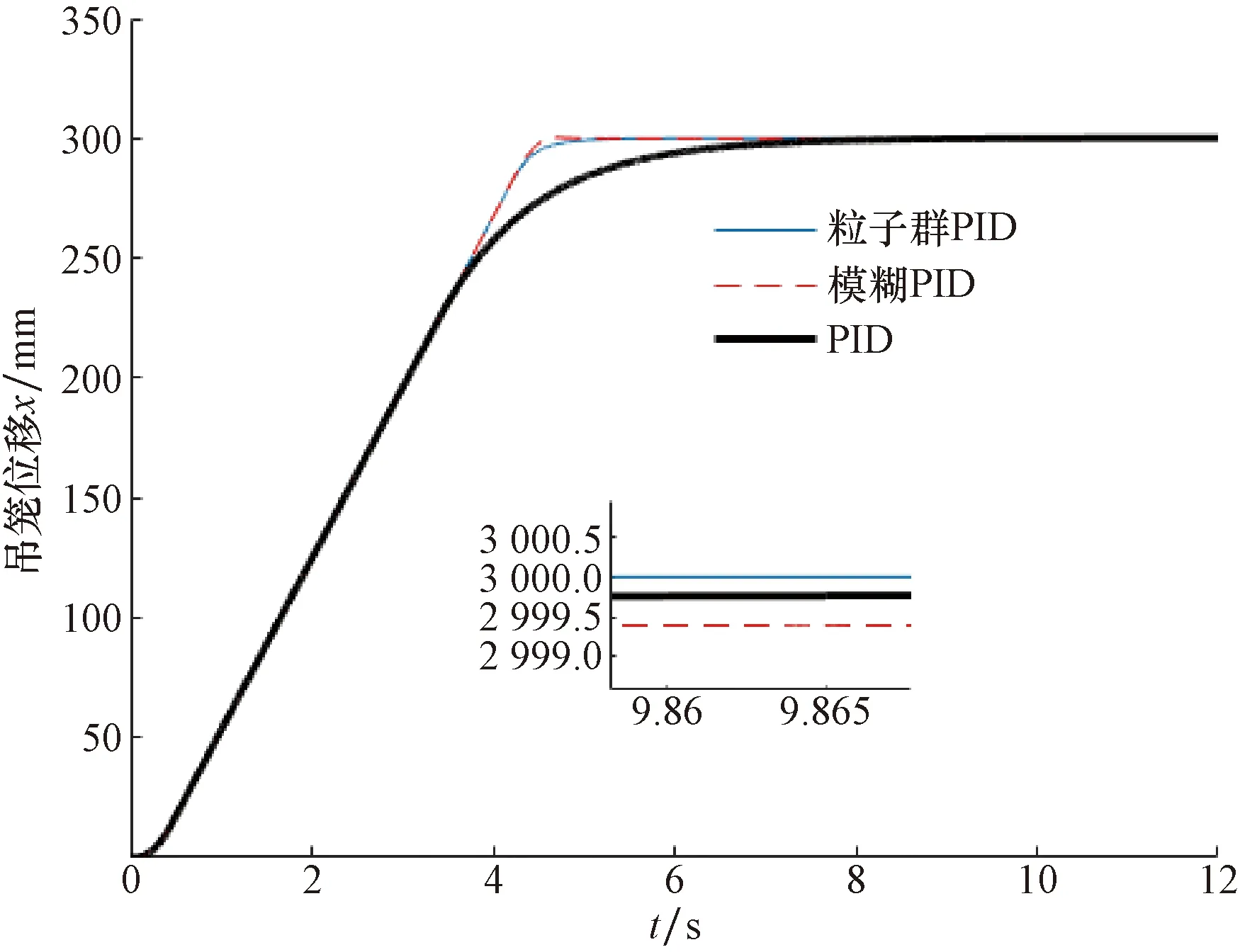
图12 位置响应曲线
根据表4所示,在PID系统下增加模糊算法,吊笼到达位置响应时间提升33%;粒子群优化PID系统响应时间相较于PID控制系统提升38%,相比模糊PID提升6%,系统稳态误差分别提升62%、98%。

表4 稳态误差
通过仿真结果可看出:粒子群PID控制器相较于传统PID以及模糊PID,控制精度更高,到达稳定状态速度更快,控制效果更加优异,具有良好的调节能力与稳态性能。相比于手动调节PID参数的方式,粒子群优化算法可以自动地搜索最优参数组合,从而避免了人工调参时产生的误差和不确定性,同时也可以提高参数整定的效率和精度。
5 结论
对施工升降机驱动装置进行分析,建立了控制系统模型与系统动力学模型,设计了基于粒子群优化的PID控制器,利用MATLAB/Simulink 与ADAMS 联合仿真的方法,对升降机驱动装置的控制系统进行了仿真分析,得出如下结论。
(1)相较于传统PID和模糊PID控制器,通过不断优化PID控制器的参数来提高系统的跟随性能和响应速度。它可以在不需要太多人工干预的情况下,自适应地调整PID参数,粒子群优化控制系统跟随性能更好,响应速度更快。
(2)在升降机控制中,PID控制器可以通过调整参数来控制升降机的速度和位置,从而实现精准的升降控制。通过采用粒子群算法在线整定PID参数,可以优化控制器的性能,使升降机能够更加平稳、准确地响应控制信号,提高安全性和使用效率。
(3)通过优化算法避免人工整定PID,大大降低劳动强度。
在今后,将建立物理样机对控制算法进行进一步研究,综合分析验证对升降机驱动装置控制性能。

