碎屑流冲击桥墩的最大冲击力影响因素试验研究
陈勇 姚昌荣 朱永发 周迅 安浩然
西南交通大学 土木工程学院, 成都 610031
碎屑流是指在崩塌或滑坡的运动过程中形成的碎屑流体,其质量大、速度快,具有很强的破坏性,严重威胁着交通基础设施和人民生命财产的安全[1-2]。桥梁是交通网络中的重要节点,破坏后抢修难度大,造成的损失十分严重。近年来,碎屑流冲毁桥梁的事故屡有发生。2016 年,雅康高速公路天全段部分山体滑坡,碎屑流冲毁了在建的8 根桥墩;2020 年,雅西高速“9·20”高位山体崩塌引发碎屑流,导致姚河坝特大桥损毁。不同于单个滚石作用下的冲击,碎屑流冲击作用机理更复杂,且具有摩擦碰撞、时滞效应、分布作用等特性。冲击力是冲击效应最直接的衡量指标[3]。实际地质灾害中,碎屑流的冲击工况复杂多变,在设计过程中须定性分析。因此,有必要对碎屑流冲击桥墩的演化过程及最大冲击力影响因素进行研究,为工程设计提供参考。
关于碎屑流冲击结构物的动力学研究主要包括理论方法、数值模拟方法和模型试验方法。理论研究方面,碎屑流细颗粒具有高速远程特性,其运动特性与泥石流浆体类似[4]。关于浆体计算模型,大多研究主要基于动力学模型变形,通过推导得到不同适用条件的半经验理论计算模型。Armanini 等[5]提出适用于碎屑流冲击拦挡结构后发生反弹的冲击力计算模型。Delannay 等[6]建立了碎屑流处于过渡态时,由重力分力和惯性力组成的冲击力计算模型。此外,中国台湾、加拿大、日本等许多设计规范都是基于动力学模型进行制定的。由于公式中修正系数的变化范围较大,对计算结果会造成一定误差。数值模拟方面,碎屑流是由大量的离散颗粒组成的集合体,离散元(Discrete Element Method,DEM)作为一种处理非连续介质的模拟方法,已被诸多学者用于碎屑流研究。张睿骁等[7]采用DEM 方法,研究了刚性挡板距离和坡度对碎屑流冲击力的影响规律。Liu 等[8]采用离散元和有限元耦合的数值方法研究了碎屑流对柔性障碍物的动力学作用。物理模型试验的试验条件可控性较高,是研究碎屑流的重要方法之一,国内外学者开展了大量碎屑流冲击结构物的模型试验。Jiang等[9]进行了碎屑流冲击挡墙模型试验,基于试验结果和已有冲击力模型,重点关注碎屑流的法向冲击力及作用点,提出了一种新的半经验冲击力模型。Wang 等[10]通过物理模型试验研究了挡墙结构对碎屑流速度和堆积形式的影响。眭静等[11]根据碎屑流冲击刚性挡墙的试验结果,提出了一种冲击力力学模型,用于计算法向、切向冲击力及冲击力作用高度。冷晓玉等[12]开展碎屑流模型试验,研究了冲击坡度和颗粒级配对碎屑流运动过程的影响规律。Kim 等[13]进行了碎屑流冲击圆柱形挡流板的模型试验,研究了挡流板高度和行数对碎屑流能量耗散的影响规律。Ng 等[14]开展了碎屑流冲击双刚性拦挡结构的模型试验,研究了拦挡结构高度和距离对碎屑流冲击作用的影响。
综上,已有研究主要集中于碎屑流对挡墙、拦挡结构等构筑物的冲击行为,关于碎屑流冲击桥墩结构的研究相对较少,缺乏相关的设计指南,较少关注碎屑流冲击桥墩时的最大冲击力。因此,本文通过室内模型试验模拟碎屑流冲击桥墩的运动过程,研究碎屑流对桥墩的冲击效应,以及碎屑流冲击距离、体量对桥墩最大冲击力的影响规律,为山区桥梁碎屑流灾害防治提供一定参考。
1 试验概况
1.1 试验装置
试验装置主要包括斜槽、物料区、反力架、废料箱等部分,见图1。斜槽尺寸为2.0 m(长) × 0.3 m(宽) ×0.5 m(高),坡度为20°。斜槽侧面采用透明亚克力板材质,表面覆有网格尺寸为2 cm 的网格纸,以便统计碎屑流的运动距离。将前后挡板粘贴于斜槽中形成物料区,临时固定前挡板以便抽离,使碎屑流在重力作用下滑动。反力架由铝合金焊接而成,用于支撑固定六分力传感器及桥墩模型,其底部嵌固在地上。

图1 碎屑流物理模型试验装置
1.2 桥墩模型及测量系统
以实际工程山区高架桥为原型,跨径为25 m,桥墩墩高为10 m,直径为1.5 m,按1∶50 的比例缩尺制作双柱式桥墩模型。桥墩模型由树脂材料采用3D 打印制成,直径为0.03 m。定义来流方向一侧的墩柱称为近柱,另一墩柱为远柱。
测量系统包括六维力传感器和高速相机。两个六维力传感器与两个墩柱之间通过连接装置用螺栓连接,六维力传感器用螺丝固定于反力架上,见图2。传感器采样频率为50 Hz。在桥墩顶部、侧面布置高速相机,用于记录碎屑流的运动形态。
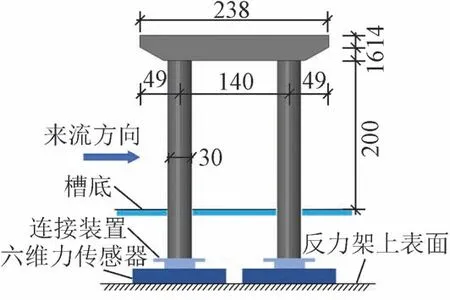
图2 桥墩模型传感器布置(单位:mm)
1.3 试验材料及方案设计
自然界中的碎屑流体通常由形状大小各异的岩石块组成,且粒径级配分布十分广泛,若在现场测量粒径分布、形状及其他参数,或在室内模型试验中再现真实的级配比例及形状是非常困难的[15]。因此,采用模型试验或数值模拟的方式研究碎屑流体的一般冲击特性时,主要采用粒径分布均匀、尺寸范围较窄的碎石来模拟碎屑流体颗粒[16-17]。
已有研究表明颗粒平均粒径与水槽宽度的比值在1/90 ~ 1/20 时,可忽略水槽宽度对碎屑流体自由滑动限制的影响[15]。考虑试验中桥墩模型的直径及斜槽装置的宽度,试验材料选择无黏性的砾石。
砾石初始粒径分布均匀,粒径分布范围为8 ~16 mm,中值粒径(D50)与水槽宽度比值为1/23,满足试验要求。砾石材料参数见表1。
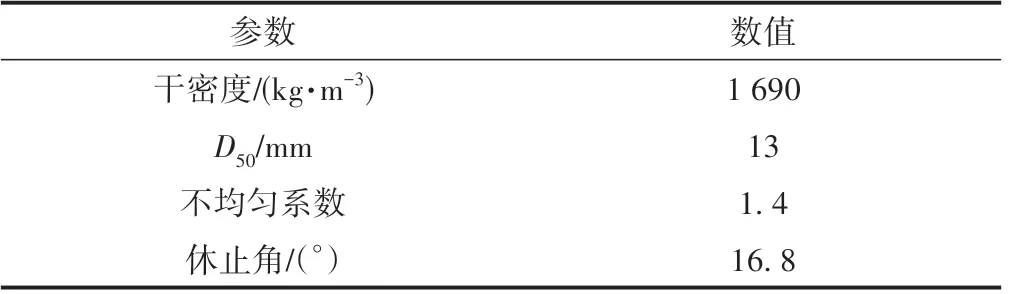
表1 砾石材料参数
本文以碎屑流冲击距离(L)、体量(V)为控制参数,通过改变初始堆积体高度(H)来实现V的变化。采用控制变量法研究碎屑流冲击距离、体量对其运动形态及冲击桥墩时的冲击力沿程演化规律。试验工况见表2,每组工况重复三次试验。
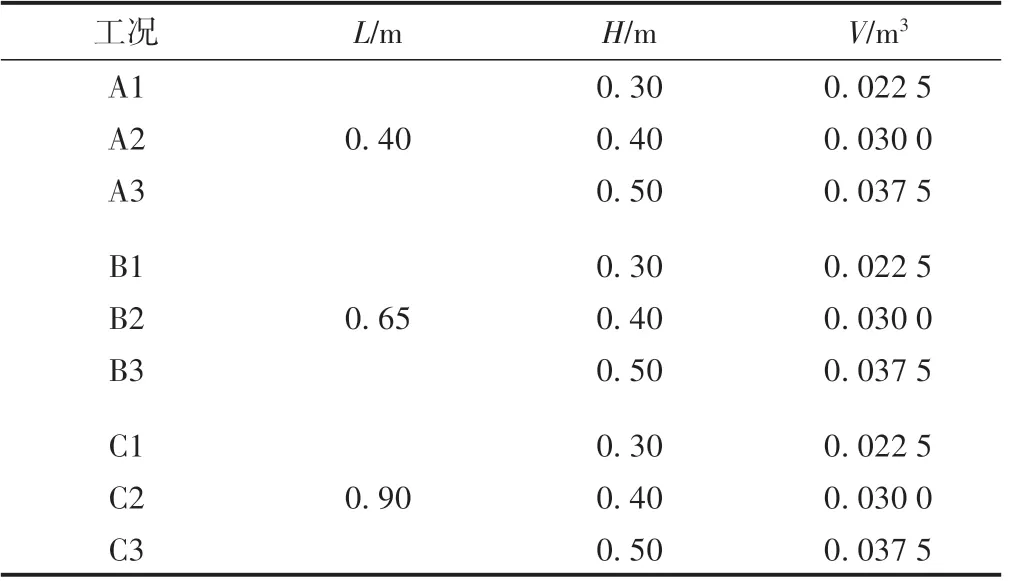
表2 试验工况
2 碎屑流运动形态分析
2.1 运动过程
以试验组B2 为例分析碎屑流运动过程。为便于观察比较,将图片旋转20°并按水平排列,见图3(a)。可知:t= 0.24 s 时,前挡板完全提起后,位于碎屑流体底部的颗粒率先下滑移动,带动前缘颗粒移动的同时上部颗粒迅速下落;t= 0.60 s 时,前缘颗粒开始冲击近柱桥墩;t= 0.77 s时,颗粒持续冲击桥墩,出现颗粒碰撞飞溅的现象,少量颗粒开始冲击远柱桥墩;t=1.60 s 时,由于颗粒之间、颗粒与斜槽之间的摩擦作用,碎屑流体稳定堆积在斜槽与桥墩之间。综上,碎屑流运动过程可分为起动加速、持续冲击、稳定堆积三阶段过程。

图3 碎屑流运动过程和颗粒飞溅效果对比
其他工况的试验现象与试验组B2类似,但有些许不同,见图3(b)。可知,当冲击距离增加后,碎屑流颗粒冲击桥墩时的碰撞飞溅程度较弱,颗粒飞溅高度更低。这主要是由于碎屑流冲击过程中,重力势能转换为动能和摩擦内能,而摩擦内能是最主要的耗能方式[17]。随着冲击距离的增加,颗粒之间、颗粒与斜槽之间由于摩擦消耗的能量更多,颗粒的冲击速度变小,冲击作用变弱。
2.2 运动速度
定义前挡板提起瞬时为初始时刻(t= 0),碎屑流前端颗粒自初始时刻到冲击近柱时刻的平均速度为vˉ1、冲击近柱后到滑出斜槽的平均速度为vˉ2。两段平均速度为对应的运动距离和运动时间之比。运动距离借助斜槽侧面网格纸进行统计,运动时间通过回放试验录像获得,绘制前端颗粒的平均运动速度,从而分析碎屑流体量、冲击距离对前端颗粒平均速度的影响规律,见图4。
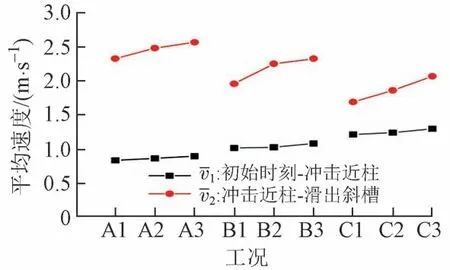
图4 各试验工况的前端颗粒平均速度
由图4 可知:①当碎屑流冲击距离相同时(工况A1、A2、A3),vˉ1和vˉ2均随碎屑流体量的增大而增大。碎屑流体底部的颗粒先下滑移动,导致上部颗粒迅速下落。本文试验中碎屑流体量越大,初始堆积体的高度越高,且上部颗粒具有更大的重力势能,因此下滑过程中产生的动能越大,速度越高。②当碎屑流体量相同时(A1、B1、C1),vˉ1随着冲击距离的增大而增大,vˉ2随着冲击距离的增大而减小。这主要是由于碎屑流运动过程中,重力势能转换为动能,冲击距离越远初始重力势能越大,自初始时刻到冲击桥墩时速度越大。而撞击桥墩后,因颗粒之间、颗粒与斜槽、颗粒与桥墩之间的摩擦作用,导致大部分颗粒堆积于斜槽和桥墩间,这种现象随着冲击距离的增加愈发明显,导致后部颗粒的能量不能有效传递到前端颗粒,因此前端颗粒的运动速度减小。
3 冲击力特征
3.1 冲击距离、体量对碎屑流冲击力的影响
分析冲击力试验数据后发现近柱受到的冲击力远大于远柱,本文旨在探究碎屑流冲击桥墩时最大冲击力的影响因素规律,因此仅分析近柱的冲击力规律。不同冲击距离下碎屑流冲击力时程演化曲线,见图5。可知,冲击力可分为碎屑流体运动时的冲击力波动段和稳定堆积后的冲击力稳定段。随着碎屑流冲击距离的增加,碎屑流自起动加速到冲击桥墩的时间增加,桥墩受到的最大冲击力减小,桥墩受到碎屑流的堆积作用也变小,相同碎屑流体量下的试验工况规律相同。原因是当碎屑流冲击距离增加时,沿程颗粒之间、颗粒与滑槽之间的碰撞、摩擦所消耗的能量增加,更多的颗粒堆积在斜槽中,导致冲击桥墩时的颗粒数减少,所受冲击力峰值也减小。
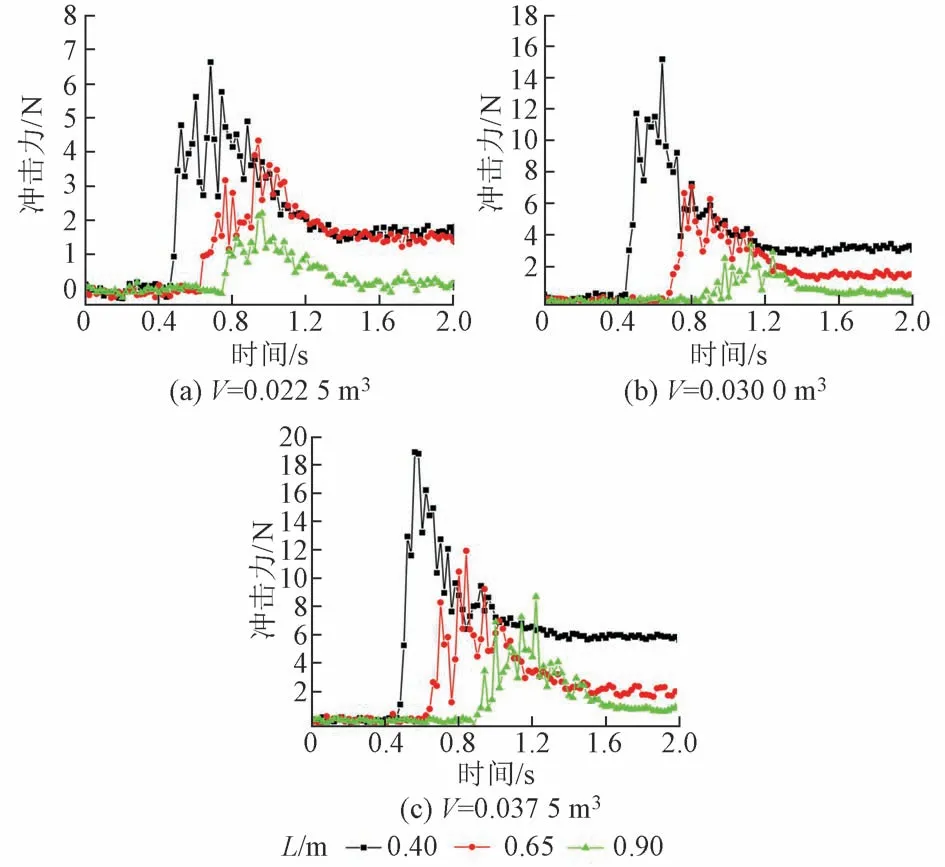
图5 不同冲击距离下碎屑流冲击力时程演化曲线
不同碎屑流体量下冲击力时程演化曲线见图6。可知,体量的增加对碎屑流开始冲击桥墩的时间影响不大。随着碎屑流体量的增加,桥墩所受到的最大冲击力增加,颗粒稳定时的堆积作用越大。原因是当碎屑流体量增加时,前端颗粒开始冲击桥墩的时间不变,意味着速度变化不大,但同一时刻冲击作用于桥墩的碎屑流颗粒数量增加,导致最大冲击力和堆积作用力增加。
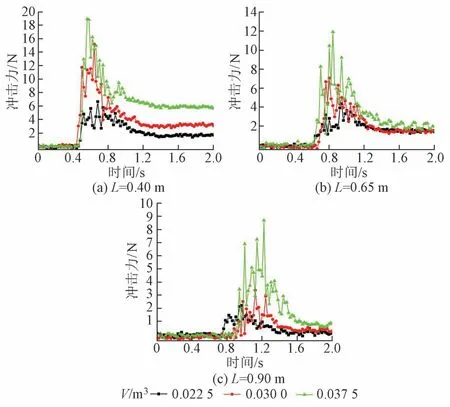
图6 不同碎屑流体量下冲击力时程演化曲线
3.2 最大冲击力影响因素分析
冲击距离、体量是影响碎屑流最大冲击力的重要因素,提取各工况下的最大冲击力数据进行曲线拟合,见图7。图中,R2为决定系数。可知:①初始堆积体高度为0.30、0.40、0.50 m 时,决定系数分别为0.983、0.998、0.991,回归拟合度较好。当碎屑流体量一致时,即初始堆积体高度相同时,最大冲击力随着冲击距离的增加呈指数函数负相关,与文献[18]规律基本一致。原因是当碎屑流冲击距离越大,颗粒碰撞飞溅的高度越低[参见图4(b)],即冲击过程中碎屑流的运动速度越小,碎屑流颗粒之间碰撞所消耗的动能越小,导致最大冲击力下降的幅度较小。②冲击距离为0.40、0.65、0.90 m 时,决定系数分别为0.869、0.998、0.973,回归拟合度较好。当冲击距离相同时,最大冲击力随着碎屑流体量的增加呈指数函数正相关。原因是碎屑流体量越大,冲击过程中作用于桥墩的碎屑流颗粒也越多,且碎屑流的运动速度相对较大,从而导致最大冲击力上升的幅度较大。
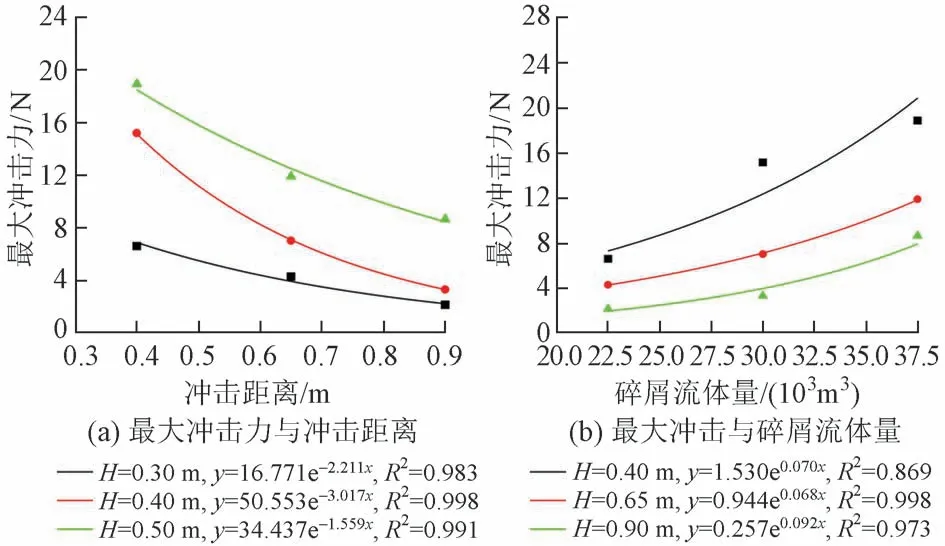
图7 最大冲击力与影响因素的拟合曲线
综上,参照文献[19]对碎屑流最大冲击力(F)与L、V之间的关系进行拟合,拟合关系式为
最大冲击力与冲击距离、体量之间的关系见图8。可知:①碎屑流冲击距离为0.90 m,体量为0.022 5 m³时,最大冲击力为2.199 N,是所有工况中的最小值;冲击距离为0.40 m,体量为0.037 5 m³时,最大冲击力为18.908 N,是所有工况中的最大值。②碎屑流最大冲击力与冲击距离成反比,与碎屑流体量成正比。在山区桥梁碎屑流灾害防治中,应优先考虑碎屑流体量更大且冲击距离更近的冲击工况。
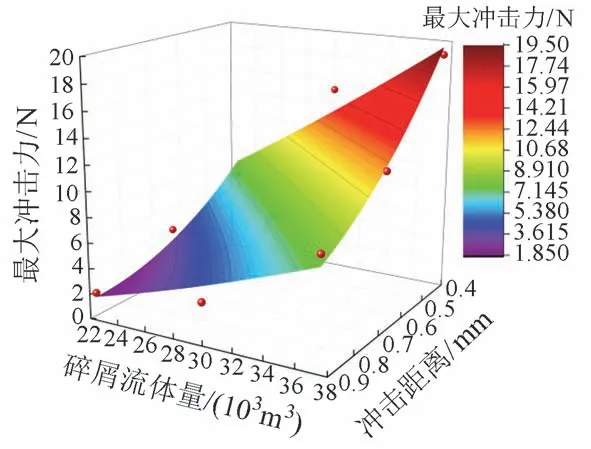
图8 最大冲击力与冲击距离、体量之间的关系
4 试验值与半经验公式预测值对比
文献[4]研究表明,具有高速远程特征的碎屑流细颗粒,其运动特性与泥石流“浆体”类似[4]。因此,采用流体动力学模型对比本文最大冲击力试验结果与常见的半经验理论公式预测结果[20]。模型表达式为
式中:P、ρmu、vmu分别为流体冲击压力、密度、运动速度;α为动力修正系数。
参考T/CAGHP 006—2018《泥石流灾害防治工程勘察规范(试行)》[21]中工程截面为圆形时的情况,α取1.0。选取最大冲击力对应时刻的运动速度作为vmu,获取方式参考文献[22],即通过相邻几帧图像上碎屑流前端颗粒的运动距离变化,计算出相应的前缘速度。同时考虑碎屑流冲击桥墩的作用面积,桥墩直径取0.03 m;通过回放试验录像获得各工况下碎屑流在桥墩上的作用高度(0.02 ~ 0.09 m)。半经验公式为
式中:b为桥墩直径,m;h为碎屑流作用高度,m。
对比不同工况下桥墩最大冲击力的试验值与半经验公式预测值,见图9。可知,半经验公式预测值与试验值最大误差为23%,各工况下两者的数值差异较小,可见半经验公式能够较好地预测碎屑流冲击桥墩时的最大冲击力。不同工况下的半经验公式预测值比试验值平均高18%,可见采用半经验公式计算的最大冲击力偏保守。

图9 最大冲击力试验值与半经验公式预测值对比
受试验条件的限制,未能模拟出碎屑流冲击桥墩过程中实际的地质环境,如本文斜槽底部平整、无明显起伏,碎屑流冲击距离、体量变化范围小等;碎屑流的颗粒粒径考虑较为单一,没有考虑含水量、块状黏性物质等,因此试验中未能体现出碎屑流运动过程中的粘黏、破碎、筛分等现象。此外,本文未考虑试验装置的尺寸效应。试验条件的限制和未考虑试验装置尺寸效应对碎屑流体的运动形态、速度、冲击力时程演化等具有重要影响,后续可开展不同尺度的模型试验进行研究。
5 结论
1)试验过程中再现了碎屑流起动加速、持续冲击、稳定堆积的三阶段过程。在撞击桥墩前,碎屑流的运动速度随冲击距离和体量的增大而增大;撞击桥墩后,运动速度随冲击距离的增大而减小。
2)碎屑流冲击距离、体量是影响碎屑流最大冲击力的重要因素。最大冲击力随冲击距离的增加呈指数函数负相关,最大冲击力随碎屑流体量的增加呈指数函数正相关。
3)基于流体动力学模型的半经验公式能够较好地预测碎屑流冲击桥墩时的最大冲击力,预测值比试验值平均高18%,最大预测误差为23%。采用半经验公式预测的最大冲击力偏于保守。

