低轨卫星多目标无源定位到达时差分选方法*

徐 鹏，雷 同，熊 炼，欧阳鑫信

（1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学移动通信重点实验室，重庆 400065；3.电子科技大学 信息与通信工程学院，四川 成都 611731）

0 引言

无源定位是指通过观测站探测目标辐射源自身发出的电磁波或散射的非协作信号，然后通过估计待测目标的定位参数并求解其定位方程，最终得到目标的运动状态及位置信息。同时由于观测站不向外辐射信号，因此无源定位具备探测距离远、隐蔽性强、反隐身能力强、生存力高等优势，在现代信息化战场中能有效提高定位系统的生存能力[1-3]。

无源定位系统可以分为单站无源定位系统和多站无源定位系统两大类，其中单站定位系统通过单个观测平台持续观测目标辐射源，逐渐积累定位信息，最终获取目标位置信息，尽管其具有设备简单、使用灵活的特点，但难以胜任战场中的复杂电磁环境、实时定位的要求[4]。多站定位系统有双观测站定位、三观测站定位等，其中较为常用的双观测站无源定位系统由两颗相距较近且时钟同步的低地球轨道(Low Earth Orbit，LEO)卫星、地面雷达接收站、定位数据处理中心等基本设施组成。该系统主要通过利用LEO 卫星的运行特性，即运行速度较快，可在一段时间范围内观测大量定位参数，如到达频差、信号到达时差(Time Difference Of Arrival，TDOA)、接收信号强度、到达角度等参数，以确定辐射源及其载体平台位置[5]。故相较于单站无源定位系统，多站无源定位系统具有定位时间短、定位精度高的优点[6-7]。

在LEO 卫星无源定位系统中，主要利用待定位目标的定位参数，通过求解相应的位置定位方程，得到目标的具体位置信息，最终实现目标定位跟踪。但若存在多个待定位目标且数量未知时，不同目标的定位参数混合，需首先对获取的观测数据集进行定位参数分选，才能针对性获取某个目标的准确位置信息，其中较为常用的方式为多站时差参数分选。

通过利用到达卫星的雷达辐射信号存在时差信息这一特征进行分选，在较短的时间范围内卫星与辐射源的相对位置变化较小，因此其时差信息稳定，故利用时差信息作为定位参数进行分选的可靠性较高，可得到较为准确的目标位置信息[8]。

针对定位参数分选问题，学者们的现有研究提出了不同的方法和理论，并取得了一系列显著成果[9-17]。文献[18]提出了一种基于递归拓展直方图的时差分选方法，该方法主要解决不同重频形式雷达信号在直方图中所对应的时差信息分布情况，但不足在于直方图噪声影响较大，容易造成后续分选出现漏分以及漏警的情况。文献[19]提出了一种基于数据场聚类与时差结合的信号分选方法，其主要解决了多站时差分选方法中由于存在失配信号导致的高漏警率问题，在时差分选的基础上通过K-means 聚类算法处理失配信号集合，但该方法无法有效降低虚警率和噪声的影响，且该方法仅适用于凸状簇数据。文献[20]采用迭代和贪婪策略优化代价函数更新聚类簇中心，克服了K-means 算法对具有离群值的数据集聚类效果差的问题，但其在参数量较大时聚类效果欠佳。文献[21]将数据集中的每个对象视为单个类，并计算类间的最小距离；合并类之间距离最小的类；然后，更新数据集并重新计算类间的距离；不断迭代，直至最后只剩一个类。该算法解决了部分K-means 不能解决的非凸簇问题，但其时间复杂度较高，同时难以处理不同大小和不同形状的簇，且该算法需要用户定义簇数目作为最终聚类结果，难以胜任定位目标数未知的场景。文献[22]通过数据集密度阈值来控制簇的扩张。通过将密度足够高的区域划为簇，且具有较低的噪声敏感性，能够在空间数据库中发现任意形状的聚类结果，但该类方法需处理每个数据对象，其运算效率较低，难以胜任大数据集。

综上所述，上述定位参数分选方法均是在一定范围内适用，局限性明显、优缺点并存，能相应地解决具有某些特征的数据聚类分选问题。

为有效解决LEO 卫星多目标无源定位场景中的定位参数分选问题，本文基于网格和密度聚类方法的基本原理，并充分考虑定位场景中的数据集特征，同时引入网格密度波谷概念和位置相连原则解决目标间数据错误聚类问题，构建多目标TDOA 参数聚类分选模型实现定位参数分选，最终通过LEO 卫星定位场景下的多目标TDOA 数据检验本文方法的聚类效果。

1 卫星定位场景介绍

1.1 LEO 卫星定位原理

本文所考虑的定位场景主要由LEO 卫星、目标辐射源、数据处理中心等组成，如图1 所示。

图1 LEO 卫星定位示意图

其中卫星同轨运行，均处于目标信号辐射范围内，由于信号距卫星的路径和径向速度不同，当目标辐射源向外发送信号时，卫星间会先后接收到辐射源发送的信号，并将其传输给数据处理中心做进一步处理，根据式(1)可获取TDOA 定位参数。

式中，c为光速；r1、r2分别为卫星的位置矢量；r为目标辐射源的位置矢量。

同时鉴于LEO 卫星移动速度较快，平均速度可达7 km/s，而待测目标速度一般为地表静止或慢速运动目标，其速度相比卫星速度可以忽略，因此在一段时间范围内，通过观测多个目标辐射源可获取大量TDOA 参数，并对其做聚类分选处理，最终通过相应的定位方程解算，便可得到各个目标的准确位置信息[23]。

1.2 TDOA 定位参数特征

为充分利用定位场景中目标辐射源的TDOA 数据集特征，并以此为基础针对性设计聚类方案，本小节首先对数据集做TDOA 参数建模处理，具体步骤如下。

(1)根据LEO 卫星获取的TDOA 定位参数，其中包含目标的观测时间序列以及相应的TDOA 序列；在离散时间索引为k时，设xk表示第k个观测参数的相对时间点，设yk表示相应的到达时差值；

(2)在二维平面上，以xk为横坐标，yk为纵坐标，绘制时间轴与到达时差轴组成的平面图，如图2 所示。后续将利用该数据集做进一步分析。

图2 待分选定位参数数据图

根据上述步骤，本文通过多次仿真实验对比与分析，提取实际卫星定位场景下的多目标TDOA 定位参数的基本数据集特征，主要特征总结如下：

特征1：平面上单个目标对应一条曲线。较短观测时间范围内，目标曲线呈现近似线性变化特征，随着观测时间变长，线性特征逐渐消失，呈现相对复杂的非线性变化特征。

特征2：数据集密度不同，各目标所含数据量存在差异。

特征3：曲线间的相对关系上，在观测时间范围内，可能出现平行、距离近等情况。

特征4：同一时间段内，不同曲线在TDOA 幅度上呈现分离状态，两条相邻曲线被明显的空白或稀疏区域拆分，空白或稀疏区域面积越大越能区分不同曲线边界。

2 网格密度聚类

基于网格密度的聚类算法(Clustering Algorithm Based on Grid Density，CAGD)不仅具有密度聚类算法的特点，即能发现任意形状的簇，而且具有网格聚类算法运行效率高的特点。且该算法对数据集中存在的噪声数据敏感性低，具有较强的抗噪声能力[24]；同时，网格密度聚类算法具有较强的可扩展性，在数据集规模较大的情况下，其聚类质量仍能得到保障。

2.1 CAGD 算法流程

网格与密度聚类算法的结合，其主要算法思想是借鉴其各自聚类算法的优点，即通过划分数据集空间，形成网格框架，并将数据对象映射入网格单元内寻找稠密网格单元间的相邻网格，最终获取数据集中一个类簇。CAGD 算法具体流程如下：

(1)由分割参数划分数据集D的数据空间，得到网格单元集合G={g1,g2,g3,⋅⋅⋅,gn}。

(2)将数据集D中的所有数据对象xi映射到其对应的网格单元中。

(3)根据密度阈值参数，确定稠密网格单元和稀疏网格单元。

(4)在网格单元集合G中随机选择稠密网格，以稠密网格单元为聚类起点，查找此网格单元的最大连通区域qi，并从集合G中剔除找到的稠密连通单元格。

(5)以网格单元集合G内是否存在稠密网格单元为依据，若存在稠密网格，则需重复执行步骤(4)，最终得到稠密网格单元的最大连通区域集合Q={q1,q2,q3,⋅⋅⋅,qn}。

(6)输出最大连通区域集合Q，其中每一个qi中的数据即是一个类簇。

2.2 CAGD 算法应用

网格密度聚类算法在雷达信号分选、轨迹数据聚类[25]、流式数据聚类等场景均有应用，且在这些应用场景中其聚类质量较好，主要在于网格密度聚类算法相较于其他传统聚类算法有着诸多优点，比如能找到任意形状的簇且运行效率高，抗噪能力强等。但不同的应用场景，其数据集特征不同，因此所使用的网格密度聚类算法也有所差异，一般都是基于网格密度聚类的核心思想设计聚类分选方法，如在雷达信号分选场景，针对多密度雷达信号问题，设计了一种基于动态网格多密度聚类算法[26]，在流式数据聚类场景中，同样根据流式数据集的特征，采用基于网格密度的改进流式聚类算法[27]。因此，需根据不同的应用场景，基于网格密度聚类算法的核心思想，结合场景中的数据集特征，有针对性地设计聚类方案，才能有效解决本文中TDOA 定位参数的分选问题。

3 多目标TDOA 定位参数分选方法

本文根据场景中TDOA 数据集特征，借鉴网格密度聚类方法的核心思想，并以此为基础进一步提出密度波谷概念及位置相连原则，构建定位参数分选模型，最终解决定位参数的聚类分选问题。

首先，以网格划分数据集，对单位时间上的网格单元，基于网格密度聚类思想进行初步类簇分选，并以网格密度波谷位置对相应类簇做进一步拆分；然后根据位置相连原则，对不同单位时间的簇进行簇间合并，最终根据各类簇中的密度阈值及拟合参数确定TDOA 参数聚类结果。模型框架图如图3 所示。

图3 多目标TDOA 参数分选模型框架图

3.1 网格划分

传统密度聚类主要依据数据点对象邻近区域的密度是否超过阈值，判断是否将其作为核心点并将该点分到与之相近的类中。该方法克服了基于划分聚类算法在非凸簇数据集的不足，可应用于在带有噪声的数据集中发现任意形状的簇。但不足在于，基于密度的聚类算法需要处理数据空间中的每个数据点，其运行效率在数据量较多的情况下表现不佳。而网格聚类，通过引入网格单元结构，将需要处理的数据点映射入网格中，只需对网格单元做进一步处理，这在很大定程度上提高了运行效率。

因此，鉴于本文场景TDOA 参数量达到万级，首先划分网格框架，而将数据空间划分为网格的主要目的是将数据集离散化，以较少的网格单元代替较多的原始数据对象，并对网格单元做进一步处理而不是独立数据点。

本文数据空间的划分采用网格划分方法，其中划分线（面）垂直于坐标轴，每个网格单元的大小一致，即均匀网格划分的形式。同时，在划分数据空间的过程中，网格步长参数ε及密度阈值Minpts 的设置极为重要。即，较大的ε可能会把不同类的数据聚为一类；反之，较小的ε会造成同类数据被聚为不同类，这都影响了聚类的精度，同时也增加了算法的难度，一般根据实际聚类情况合理调整参数。而密度阈值的设定，主要采取的方法为计算网格单元中网格密度的平均值，即Minpts 的值为：

式中，N为网格单元数量，Deni为网格单元密度。

3.2 单位时间参数分选

在网格框架下，将数据集中的每个对象映射到网格单元内，再根据定位参数特征4，可探测同一单位时间内不同曲线之间的空白或稀疏网格，得以初步界定不同曲线的边界，并基于网格密度聚类基本原理，根据相邻稠密网格单元，生成初步分选簇，如图4 所示。

图4 初步分选簇聚类结果

如图4 所示，在7～8 s 时间范围内根据空白网格位置及各稠密网格单元将数据划分为分选簇1 和分选簇2。同时，根据定位场景中TDOA 定位参数特征1、特征3 可知，存在某一分选簇内包含多个目标数据的情况。本文通过利用目标TDOA 参数的线性变化特征，即在同一分选簇内若其数据未能拟合成一条误差较小的曲线，判断该簇包含多个目标数据，为保证聚类质量，则需对该类簇做进一步拆分处理，具体步骤如下。

(1)获取单位时间内簇C中包含的网格单元数量N；

(2)若N≥3，则进一步计算该簇数据的均方根误差：

式中，h(⋅)为该簇数据经最小二乘法所生成的拟合函数，表示该时间点处拟合到达时差与实际到达时差的欧氏距离，xi为该簇内某一数据点的时间值，yi为其对应的到达时差值，m为数据总量；

(3)若均方根误差低于误差阈值，则不对该簇拆分，反之需对其做进一步拆分处理。

其中误差阈值可由式（4）计算所得：

式中，xmax代表该簇数据的最大时间值，xmin为最小时间值，β为该簇数据生成拟合函数的一阶系数，α为误差因子。

针对误差大于所设阈值的分选簇，引入密度波谷概念，即目标间数据可由密度较低的网格单元区分，并作为该簇的密度波谷，故可通过此网格单元位置对该簇做进一步拆分处理，具体拆分步骤如下。

(1)统计该簇内各网格单位密度Deni；

(2)获取密度波谷位置，即该网格单元编号i，并在该波谷位置对该簇做进一步拆分处理，最终在该单位时间内生成新的分选簇，如图5 所示。

图5 密度波谷拆分结果图

3.3 目标数据簇间合并

考虑到在多目标LEO 卫星无源定位场景中，数据集分布存在明显的线性变化特征，且各目标间数据有距离近、互相平行等情况，仅采用网格密度聚类算法，难以有效区分不同目标间数据，容易将不同目标数据聚为一个类簇，造成聚类质量较差的情况，如图6 所示。

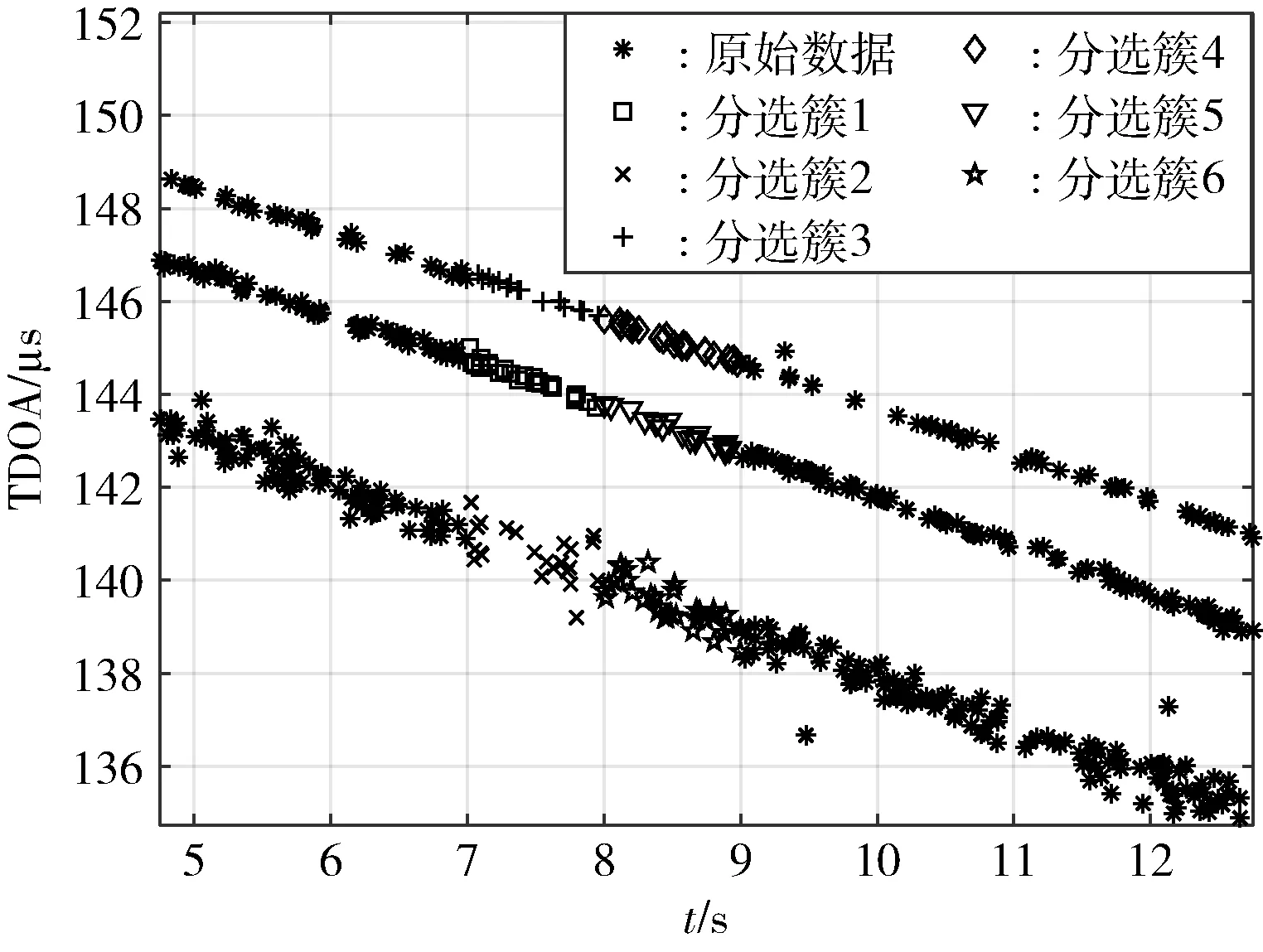
图6 多簇位置相连

其中，如分选簇2 与分选簇5 和分选簇6 均存在相邻网格，分选簇3 与分选簇4 及分选簇5 同样均存在相邻网格，即簇2 与簇5、簇6 位置相连，簇3 与簇4、簇5 位置相连。若仅采用传统网格与密度聚类算法，会将其合并为同一个簇，并不符合定位场景中的参数分选需求，故本文引入位置相连原则，即结合竞争思想，充分利用TDOA 数据集特征，进一步计算分选簇各自对应的线性拟合参数，然后选择双方最为匹配的簇进行簇间合并，以此构建最大连通域，如图7 所示。

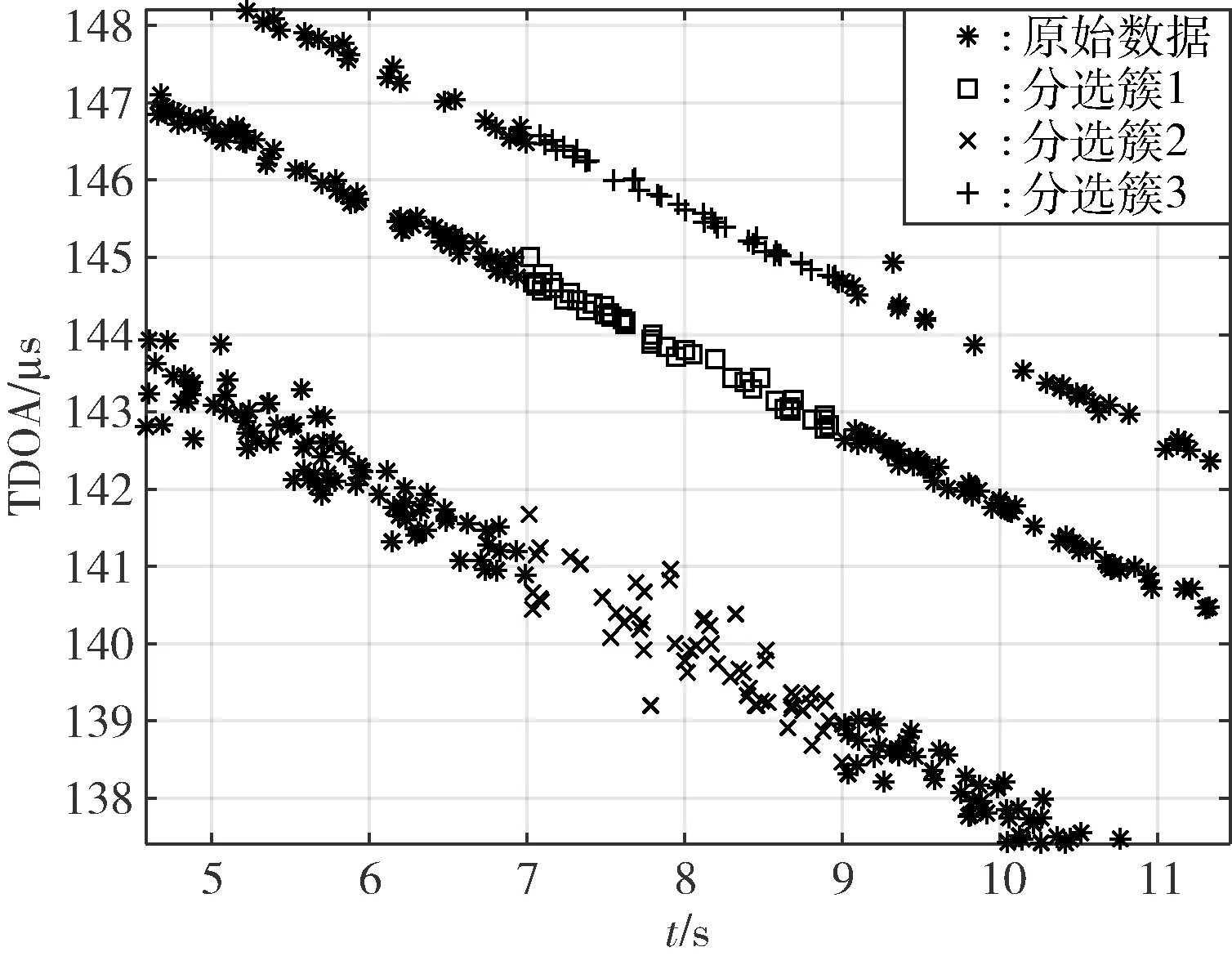
图7 部分簇间合并结果图

根据上述思想并结合3.2 小节获取的初步分选结果，可得到TDOA 参数的最终分选结果，具体步骤如下所示。

(1)将第一秒内的初步分选结果存入簇集合Cluster，并设置J=2；

(2)将第J秒内所有分选簇与Cluster 中的各簇根据位置相连原则进行簇间合并；

(3)第J秒处理完毕后，令J=J+1，重复执行步骤(2)，直至J为最大观测时间；

(4)搜索剩余未连接数据点，与已有簇的拟合曲线进行匹配，误差小于门限的并入对应的簇中；

(5)在簇集合Cluster 中，根据各簇的密度阈值，判断达到要求的簇作为最终聚类结果。

4 实验仿真

本文实验所采用的计算机硬件配置为Intel Core i5处理器(主频2.4 GHz)、16 GB 内存；实验的软件环境为Windows 10 操作系统，采用MATLAB 编程实现。

4.1 仿真环境及参数设置

为验证本文所构建模型的可行性和有效性，本实验选取三组数据集进行测试。数据集均为模拟实际LEO卫星定位场景下获取的多目标辐射源信号的TDOA 参数。其中Data1、Data2 数据集中卫星高度均为500 km，Data3 卫星高度为750 km，各目标分布范围为东经112°～120°、北纬10°～22°，并根据不同LEO 卫星观测速率及精度生成TDOA 数据。为模拟噪声环境，均加入5 %以数据集总量为基础的干扰数据，其数值为在整体数据范围内生成的均匀随机数。同时，经过多次实验证明分选模型中网格步长参数ε=1、密度阈值Minpts=3、误差因子α=7 时聚类效果最佳。

4.2 聚类结果对比

鉴于数据集为非凸的，因此并不适用基于划分或层次的聚类算法，故本文的对比算法主要采用网格与密度聚类算法，即DBSCAN 算法、CLIQUE 算法。且通过两种常用的外部聚类评估指标对其聚类质量进行评价：纯度、F 值，2 种指标的取值范围均为[0，1]，取值越大表示聚类结果和真实情况越吻合。

其中纯度的定义如下：

其中，N表示总的样本数；Ω={ω1,ω2,⋅⋅⋅,ωK}表示一个个聚类后的簇，而C={c1,c2,⋅⋅⋅,cJ}表示正确的类别；ωk表示聚类后第k个簇中的所有样本，cj表示第j个类别中真实的样本。

F 值的定义如下：

其中，p表示聚类准确率，r表示聚类召回率，β一般取值为1。

各数据集的详细信息及实验对照结果如表1 所示。

表1 聚类效果对比

为了更加直观地对比本文方法和DBSCAN 算法、CLIQUE 算法的聚类质量，给出各方法的聚类结果图，如图8 所示。

图8 聚类结果对比

从图8 可以看出，本文方法在该定位场景下的TDOA 参数分选均优于对比聚类方法。在数据集Data1中，通过利用数据集的线性变化特征并结合位置相连原则，能有效实现定位参数分选。数据集Data2 和Data3中，部分目标数据相距较近，容易存在将不同目标数据聚为一类的情形，故利用目标间数据的密度差异，结合密度波谷位置对簇做进一步拆分处理，使得聚类效果更佳。

图9、图10 为本文方法与DBSCAN 及CLIQUE 方法的纯度和F 值对比图。

图10 聚类F 值对比

通过表1、图9 和图10 可以得出，本文方法与DBSCAN 算法均优于CLIQUE 算法，同时通过图9 可以看出，本文方法与DBSCAN 算法的聚类纯度在数据集Data1 与Data2 内数值接近，其主要原因在于纯度的总体计算思想主要为通过聚类正确的最大样本数除以总的样本数，因此，通过适当调整DBSCAN 算法的输入参数便能最大程度分选出目标数据，即有着较高的纯度，而F 值则是综合考虑准确率和召回率，更具代表性。

为进一步验证本文模型在实际定位场景中的聚类效果，本文利用实际卫星定位数据做对比实验，该数据来源为合作研究所提供，原始数据如图11 所示。

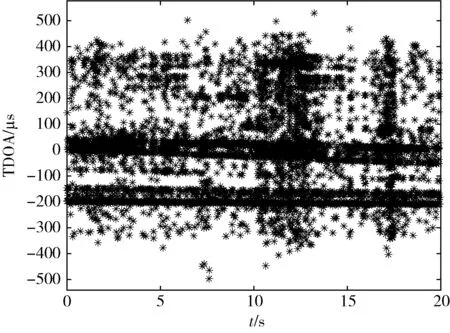
图11 实际定位数据图

鉴于实际定位场景中，目标数未知且不存在真实数据标签，因此聚类评估采用内部评价指标，即本文采用轮廓系数验证聚类质量，其定义如下所示：

其中，a(i) 表示目标数据i与同簇之间其他目标的平均距离，b(i) 表示目标数据i与不同簇之间的平均距离，S(i) 的取值范围为[-1,1],该值越大表明目标与自己所在簇之间的匹配关系度越高，与其他簇的匹配关系度越低。

针对该实际数据，聚类结果如图12 所示。

图12 轮廓系数结果图

从图12 可以看出，本文方法在实际卫星定位场景中的聚类质量均明显优于对比算法，具备一定的实际应用价值。

5 结论

针对LEO 卫星无源定位系统下目标数量多、定位参数混杂，难以通过现有单一聚类算法对其进行有效分选问题，本文结合网格与密度聚类的基本原理，确定簇的初始轮廓，并根据目标数据集特征，有选择性地在密度波谷位置进一步拆分簇，从而解决不同目标数据被划分为同一簇的问题。最终，针对多簇网格单元相邻，通过位置相连原则合并属于同一目标的簇，构建最大连通域得到最终定位参数分选结果。仿真实验结果表明，本文方法在测试数据集中的聚类纯度及F 值均能达到90 %以上，明显优于对比聚类算法在该定位场景下的应用，很大程度上解决了LEO 卫星无源定位中多目标的TDOA 参数聚类分选问题，为实现进一步的目标定位跟踪提供了有力保障。