LEO 卫星TDOA/DOA 定位性能分析*
周 艳,屈德新,张更新
(南京邮电大学 通信与信息工程学院 通信与网络技术国家地方联合工程研究中心,江苏 南京 210023)
0 引言
低轨互联网卫星系统作为低密度地表用户接入全球互联网的快捷途径,获得了快速发展。“星链”等低轨互联网卫星系统可以提供宽带化的低成本、全球覆盖的互联网服务,该系统规划4.2 万颗的卫星数量可实现全球化高带宽的卫星波束覆盖[1]。卫星覆盖区域广、用户多、易受干扰,卫星受到干扰时需要对干扰源位置的可靠定位和排查,是卫星系统正常运行必要条件。
目前干扰源卫星定位的常用体制是双星到达时间差(Time Difference of Arrival,TDOA)/到达频率差(Frequency Difference of Arrival,FDOA)定位系统和多星时差定位系统[2]。双星时/频差定位使用卫星数量较少,因此应用最多。但是,双星时/频差定位体制存在定位误差显著增大的“盲区”,这些盲区存在造成定位性能不稳定的问题。对应具有星载相控阵天线的卫星,利用单颗卫星对干扰源波达方向(Direction of Arrival,DOA)的测量,可对地表干扰源完成定位任务,但是定位误差较大。TDOA/DOA 混合定位系统可以解决上述问题,具有更稳定的性能。
对于TDOA/DOA 混合定位,测量时差和测量角的方程是关于目标源位置的非线性方程。定位算法的关键是处理这些非线性方程[3-4],文献[5]通过在两个观测站观测到的到达时间差和到达角的混合测量和未知源位置之间构建新的关系,进而得到一个简化辐射源位置解。文献[6]结合了时差和到达角对目标源进行定位,但只使用一个观测站的测向信息,为了获得更精确的定位估计,可以使用多个观测站的测向数据再联合时差数据进行位置估计。文献[7]针对双星定位场景,提出了几种闭式解算法,用以有效估计目标源位置,但未考虑卫星位置误差给定位误差带来的影响。
目前TDOA/DOA 联合的定位方法由已广泛应用于蜂窝移动网络定位场景中,然而,并没有给出目标源的定位误差几何稀释精度因子(Geometric Dilution of Precision,GDOP)的分布形式。对于现有的CGCS2000 国家大地坐标系与1984 世界大地坐标系,它们采用的参考椭球非常接近,仅扁率的细小差别会造成同一定位点在两个坐标系中的值有微小差异,在卫星导航定位中,要求精度大于两坐标系的点位坐标差异,不需要顾及坐标系框架间的差的差异,那么WGS84 下的定位结果可视作CGCS2000 下的定位结果。所以本文对于双星TDOA/DOA 联合定位系统,在文献[8]所提出的定位闭合形式算法基础上,联合双星的DOA 观测量与TDOA观测量,采用WGS-84 地球椭球模型作为约束条件,建立起目标源位置参数与观测量之间的伪线性关系,从而计算出目标位置解。最后对双星TDOA/DOA 定位的星下点附近的GDOP 进行仿真和分析,比较分析了双星时/频差定位的星下点附近的GDOP 分布,验证了算法对目标源位置低敏感性。
1 定位模型
假定TDOA/DOA 的双星干扰源定位系统中低轨卫星SV1、SV2,在Oe-xyz球心坐标系下卫星位置为x1=[x1,y1,z1]Τ,x2=[x2,y2,z2]Τ,地面干扰源位置坐标为x=[x,y,z]Τ,对到达卫星的时间差和入射方向进行测量,建立定位方程,其定位模型如图1 所示。
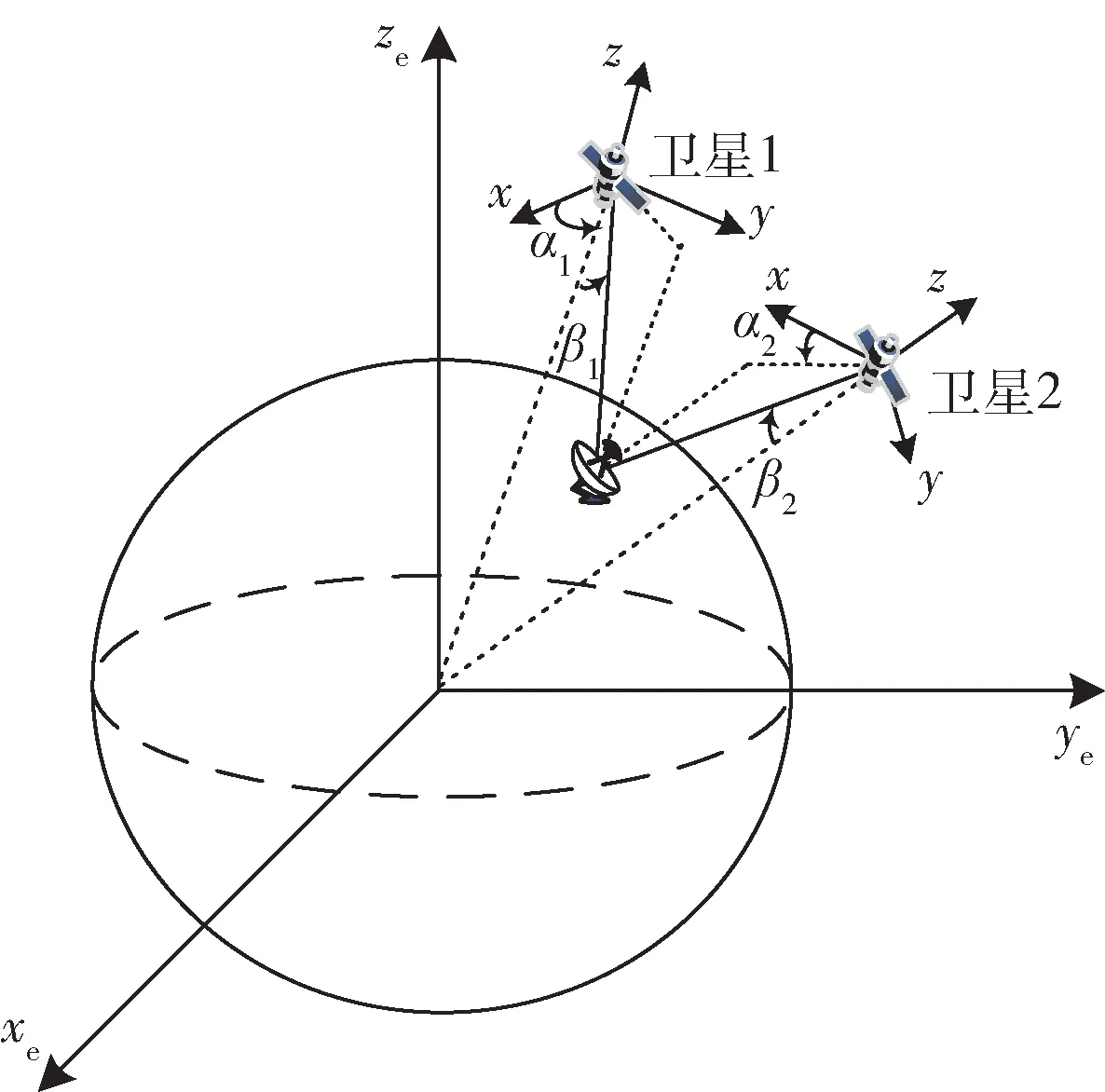
图1 双星TDOA/DOA 定位几何示意图
假设双星测得的目标源信号真实到达时间差为td,则有时差方程:
DOA 测量得到的到达卫星1、2 的方位角α1、α2和仰角β1、β2满足方程:
其中,i=1,2,(xi-x)xb、(xi-x)yb、(xi-x)zb代表矢量xi-x在星体坐标系Ob-xyz下坐标轴x,y,z方向上的投影长度。为了将地球坐标系转换到星体坐标系,需要建立坐标变换的旋转矩阵M,其表达式参考文献[9]。地面干扰源位置满足地表约束条件:
式中,a为地球长轴。
对于上述定位方程,直接估计目标源位置是相对困难的,因为该模型方程与目标源位置之间是非线性的,所以本文基于文献[8]所提出的两步加权最小二乘法,将DOA 观测量和TDOA 观测量相结合,建立目标源位置参数与观测量αi,βi,td之间的伪线性关系,从而计算出目标位置解。那么上述定位方程可以用以下约束最小二乘优化问题来定解:
利用式(5)求出待估计的参数向量ξ′,对于ξ′取前三维即为目标源的位置估计值,但是可以根据ξ′所定义的估计误差来进一步提高目标源的位置估计精度,再次采用加权最小二乘法计算定位误差Δx的估计值,然后从x′减去Δx进而来提高目标源的位置估计精度。
2 双星TDOA-DOA 定位精度分析
在双星定位系统中,误差因素有随机定位误差与系统性误差,系统性误差主要源于卫星的轨道误差、卫星与接收机钟差以及大气折射的误差等,导致时差与测向的测量存在系统误差,可以通过各种系统标校来减小消除;同时随机观测噪声也会带来随机定位误差,在双星TDOA/DOA 定位模型中,随机观测误差主要包括TDOA测量误差、DOA 测量误差以及卫星位置误差,假设测量误差和卫星位置误差向量均为零均值高斯分布,且它们互不相关。
考虑到WGS-84 地球椭球模型的约束,则双星TDOA-DOA 定位的目标源定位误差的CRLB 表示为:
式中,J是x在约束条件下的梯度,即:
则双星TDOA-DOA 定位算法的几何精度因子(GDOP)为:
其中 trace 表示矩阵对角线元素的总和。
3 仿真及性能分析
本文对定位性能的仿真分析采用具备阵列天线的Starlink 卫星为例,利用STK 创建双星TDOA/DOA 定位的仿真场景,在某一定位时刻,双星的轨道高度分别是558 km 和551 km,双星的星下点经纬度坐标分别为(36°,107.5°)和(37°,105.2°)。
3.1 双星TDOA/DOA 仿真分析
在Starlink 卫星网络中,信噪比可达到9~10 dB,在该信噪比条件下,对于星载多波束天线测向,采用波束指向角高精度测试方法有望可以将测向精度达到0.01°量级,所以本文卫星的时差测量误差按200 ns 工程测量精度进行仿真试验,同时假设卫星位置测量误差和到达方向的测量误差分别设为50 m 和0.01°,定位目标点为(40°,98°),采用本文的双星TDOA/DOA 定位算法对目标点进行定位,独立观测50 次,其定位结果散点分布图如图2 所示。为了分析该方法的性能,采用蒙特卡洛重复试验进行统计分析,假定每一个目标定位点独立重复试验1 000 次,可以得到地球表面星下点附近的蒙特卡洛统计的误差分布如图3(a)所示,理论计算的GDOP 分布如图3(b)所示。图中⊕表示两颗卫星在定位时刻对应的星下点位置。
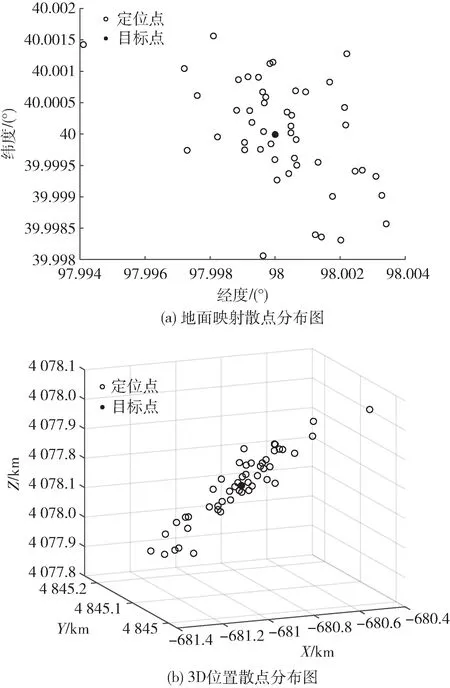
图2 双星TDOA/DOA 定位对目标点的定位散点分布图
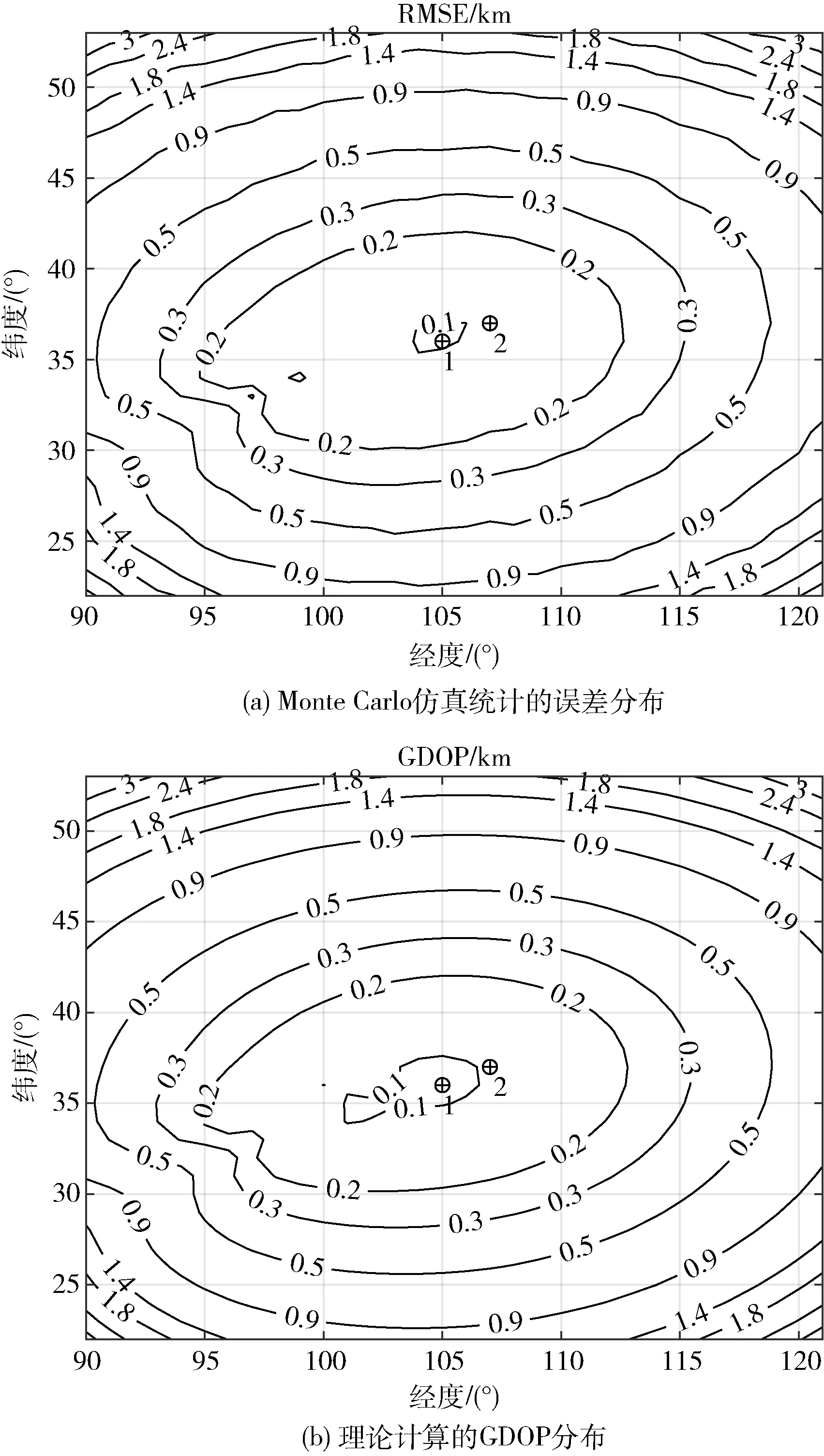
图3 双星TDOA/DOA 定位误差分布
从图2 可以看出,双星TDOA/DOA 定位技术可以实现对目标源的单次观测定位,其定位点散布在目标定位点周围,经纬度的定位误差保持在0.01°范围内,对目标源的高度定位误差保持在百米级。
通过对比图3 的(a)(b)两图,表明蒙特卡洛仿真统计的误差分布与理论计算误差的GDOP 分布趋势相同,从而进一步验证了在TDOA/DOA 定位体制下,理论计算定位误差的GDOP 分布有效性以及本文对于TDOA/DOA 定位解算方法的可行性。
对于星链卫星,星上波束是张角宽度为±44.85°的锥状波束[10],星下覆盖区的经度/纬度范围约为4°的圆形区域,仿真实验表明在这个区域内该定位算法的定位误差小于0.2 km,在卫星的最远可视范围内的地理平均定位误差为0.112 km,满足其对干扰源定位排查的需求。
3.2 目标源位置敏感性分析
双星定位系统中主要的定位技术为双星的时差/频差定位,为了分析双星时/频差定位与双星TDOA/DOA 定位对目标源位置的敏感性,利用文献[11]中的时频差定位算法参数设置,假设信号源的带宽为100 kHz,噪声带宽为0.1 MHz,积累时间为10 ms,频差测量误差为1 Hz,时差测量误差为200 ns,卫星位置测量误差为50 m,到达方向测量误差为0.1°,图4 为双星时频差定位误差三维分布以及双星TDOA/DOA 定位误差三维分布。
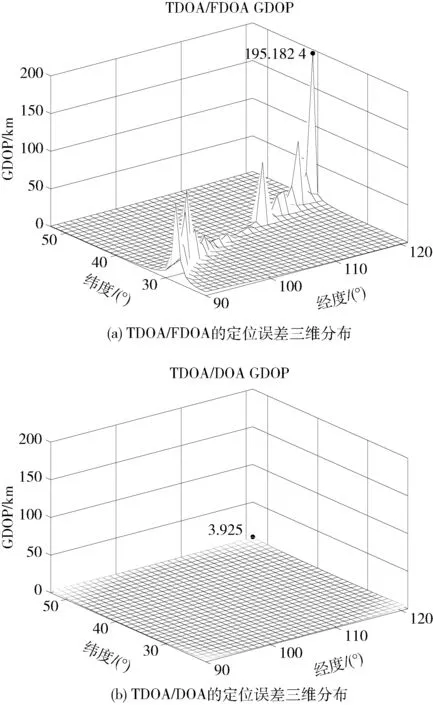
图4 TDOA/FDOA 和TDOA/DOA 的定位误差三维分布
为了进一步验证双星时频差与双星TDOA/DOA 对目标源位置的敏感性,选取了以星下点为中心,半径为2°,4°,6°,8°,10°的定位圆域上进行仿真计算,其定位误差如图5 所示。
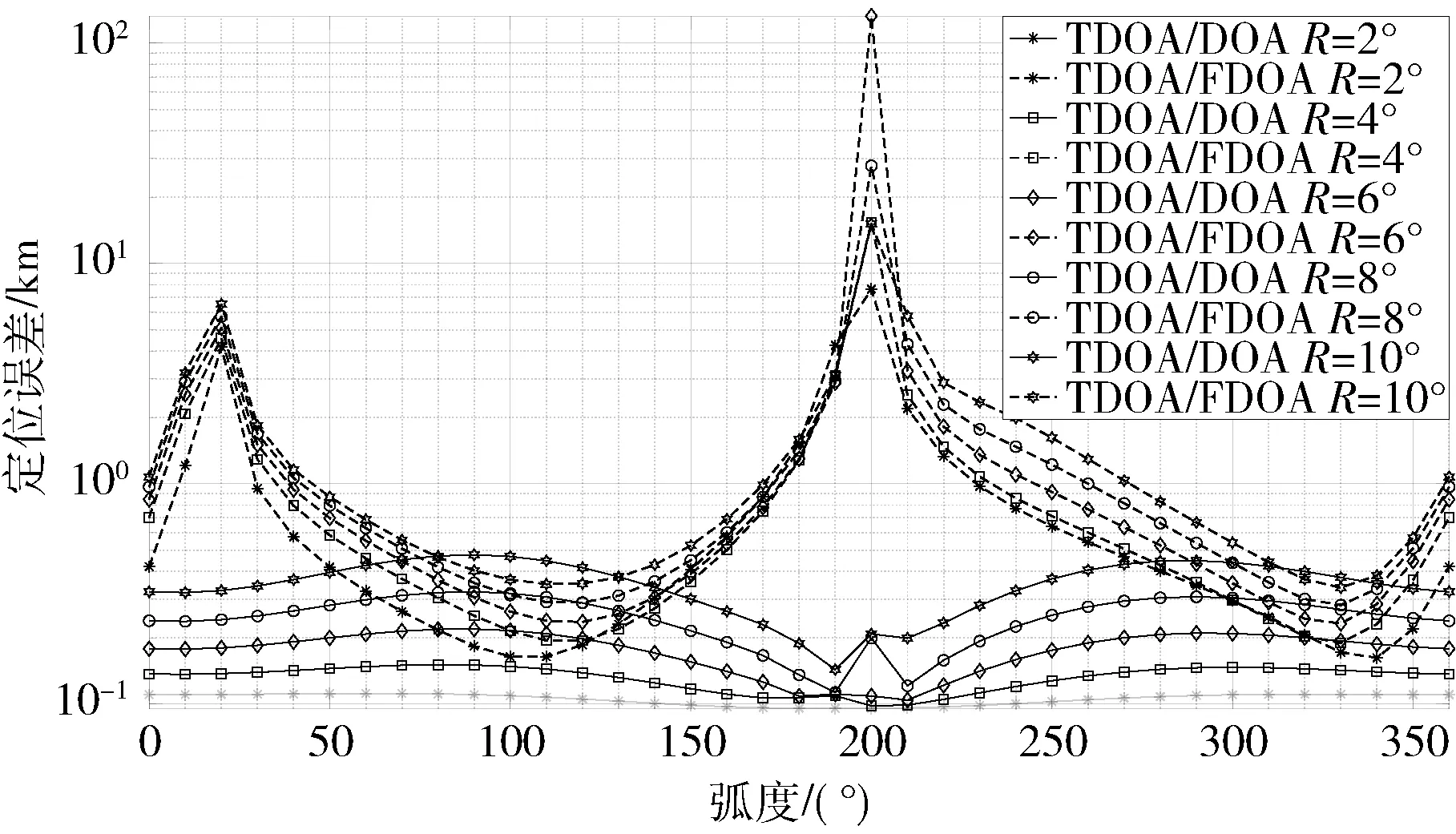
图5 半径分别为2°,4°,6°,8°,10°的圆域上定位误差
从图4(a)可以看出,双星时频差定位在部分区域存在较大的定位误差,可观测性较差,其定位误差在卫星连线方向的带状区域内敏感性较高,最大定位误差达到195.182 4 km,定位误差在卫星连线的左右两侧区域内的敏感性较低,定位误差小,定位精度高。从图4(b)可知,双星TDOA/DOA 定位在卫星连线方向的带状区域内对目标源位置的敏感性低于双星时频差定位对目标源位置的敏感性,其最大定位误差在3.925 km,远小于双星时频差定位在该区域的最大定位误差。同时,由图5 可以看出,以星下点为中心,增大定位圆域半径,即距离星下点越远,双星时频差定位与双星TDOA/DOA 定位的定位误差也会随之增大,但是双星时频差定位在弧度为20°和200°附近的目标点位置处定位性能会极度恶化,由于该弧度上的定位点位于卫星连线方向的带状区域内,该区域内多普勒频率差对目标源位置的区分能力不强,导致定位误差被几何放大,而双星TDOA/DOA 定位在整个圆域上定位误差变化差值不超过1 km,进一步验证了双星TDOA/DOA 定位体制对目标源位置的低敏感性,所以其定位稳定性更优于双星时频差的定位稳定性。
4 结论
本文针对双星定位系统,研究了基于TDOA/DOA 的联合定位技术,以WGS-84 地球椭球模型为约束条件,提出了一种双星TDOA/DOA 定位的闭式求解算法,推导了双星TDOA/DOA 定位算法的GDOP,对该算法的定位误差进行了蒙特卡洛仿真,实验结果验证了该定位算法的有效性和正确性。同时将其与双星时频差定位算法的GDOP 进行了比较,双星TDOA/DOA 定位算法对目标源位置的敏感性更低,从而可以进一步提高对目标位置定位的适应性,为双星无源定位系统的实际工程应用提供了一个新方法。

