经历建模过程 培养代数思维 发展模型意识——“方程”教学重构与思考

董文彬

（北京师范大学教育学部）

【课前慎思】

教材内容及学情分析：“方程”是北师大版数学教材四年级下册第五单元第3 课时的学习内容，也是小学数学中的一节单元核心课。“方程”的教学重构是从学生在两次前后测调研中暴露出的问题开始的。笔者对学习方程后的五年级学生进行了后测，同时对学习方程前的四年级学生进行了前测，结果显示：五年级学生在四年级下学期学习完方程之后，在面临实际问题（即便是稍复杂的问题）时，依然不愿意或不喜欢主动运用方程解决，学生对方程没有亲近感。学生解决问题的策略更多地停留或依托于算术思维，即根据条件和信息倒着想问题的逆向思考。学生只关注方程形式化的“外衣”，不认识方程的本质，没有体会到方程本身的独特价值。学习方程前的四年级学生仅有两成左右能够主动列方程刻画和描述问题，而八成左右的学生选择列算式，依然喜欢算术思维“倒”着想问题，绝大多数学生不愿意主动亲近方程，没有体会到方程在解决问题中的独特价值。

困惑：学生在学习方程前对方程已经有所了解，辨认哪些式子是方程也没有太大的困难，那么分类概括、区分等式、不等式，认识方程与等式的关系是这节课的重点吗？北师大版数学教材在学习“方程”之前有独立的“等量关系”一课，对等量关系的刻画与描述还是这节课的难点吗？这节课的教学目标究竟该如何重新定位才能回应和解决学生出现的上述问题？

思考：“含有未知数的等式叫方程”这句话有那么重要吗？它究竟是不是一个严谨的逻辑定义？方程概念的核心意义究竟是什么？算术法也可以解决实际问题，为什么还要认识方程？“算术”与“代数”的本质区别是什么？学生认识了方程就会用方程了吗？方程不可替代的独特价值和意义体现在哪儿？说到底，究竟什么是方程？方程的本质是什么？方程模型又是什么？如何在教学中着眼于发展，让学生经历方程的建模以发展模型意识的全过程？思辨至此，新的教学重构路径已跃然纸上。

基于上述分析，笔者确定了如下教学目标：在认识方程的过程中感受算术法与方程法之间的区别；感受同一个等量关系可以解决同一个情境、不同的问题；感受同一个等量关系可以解决不同情境、不同的问题；初步经历方程的建模过程，体会方程不可替代的独特价值。

【课堂实践】

一、顺应思维，感受区别，建构概念

（教师出示情境图）

师：我们去水果店买水果，看到这些水果的单价，你关心什么问题？

生：一共需要花多少元钱？

生：这个西瓜有多重，4个橙子有多重？

（教师结合学生提出的问题，分步演示课件）

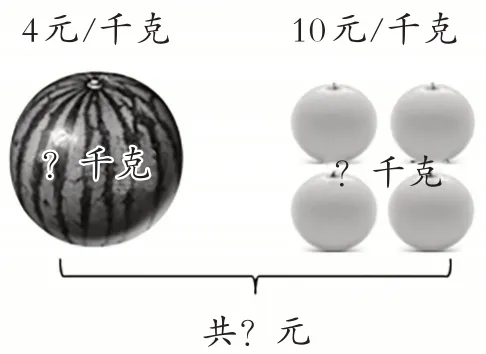
【分析与思考】在学生日常熟悉的“买水果”主题情境中，教师启发学生根据信息，自主发现和提出问题，营造有价值的“问题场”。学生自己提出的问题，更能激发群体性问题解决的兴趣和数学思考的欲望，同时为后面在问题解决中感悟算术思维和方程思维的区别做铺垫。

师：我们先来解决1个西瓜和4个橙子各自有多重的问题。（出示天平、5千克和2千克砝码各1个）用它们行吗？

生：行。

师：先称谁？

生：西瓜。

（教师课件演示：西瓜放入左盘，5千克砝码放入右盘）

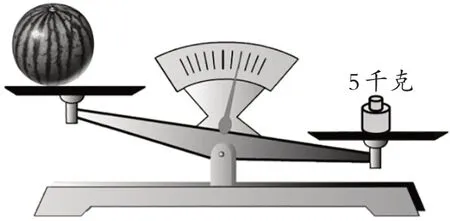
师：你知道西瓜重多少吗？

生：不知道。因为天平的状态不平衡，说明左右两盘的质量不相等。

生：虽然不知道西瓜具体重多少千克，但能知道它一定比5千克轻。

（教师课件演示：将2 千克砝码放入左盘，调整天平状态）

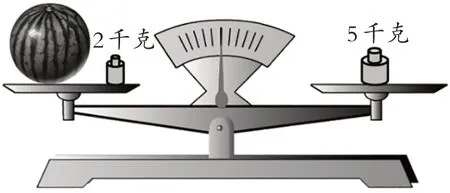
师：这回行了吗？能知道西瓜的质量吗？

生：能，3千克。

师：怎么得到的？

生：5-2=3。

（教师板书：5-2=3）

师：为什么用5-2=3来解决？

生：现在天平平衡了，西瓜的质量加上2 千克等于5千克。

师：你关注到了天平左右两盘物体的质量关系。这是一个等量关系，你能表示出来吗？

生：西瓜的质量+2千克=5千克。

生：如果把西瓜的质量看成x，那么x+2=5。

（教师板书：西瓜的质量+2千克=5千克，x+2=5）

师：西瓜的质量问题解决了，接下来我们称橙子。

（教师课件演示：4 个橙子同时放入天平左盘，2千克砝码放入右盘）

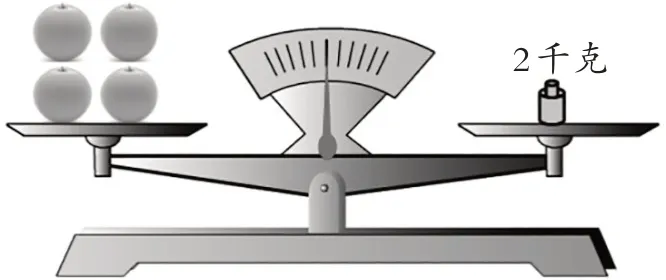
师：你知道每个橙子的质量吗？

生：0.5千克，2÷4=0.5。

师：为什么这么解决？

生：因为4个橙子的质量正好等于2千克。

师：这里也有一个等量关系，你能表示出来吗？

生：4个橙子的质量=2千克。

生：假设每个橙子重y千克，4y=2。

（教师板书：1个橙子的质量×4=2千克，4y=2）

师：刚才的问题解决了吗？

生：解决了，知道西瓜和橙子有多重了。

【分析与思考】学生在天平由不平衡逐渐逼近平衡的状态中，思考解决“1 个西瓜有多重”和“1 个橙子有多重”的问题。教师在问题解决中不回避学生使用算术法，而是顺着学生的算术思维拾级而上，启发学生关注天平左右两盘中物体的质量之间存在的等量关系，并尝试把它表示出来。在此过程中，学生自然而然地设定未知数，建构出方程，初步体会到方程其实是更简洁地表达出等量关系的过程。

（教师结合学生的回答，出示情境图）

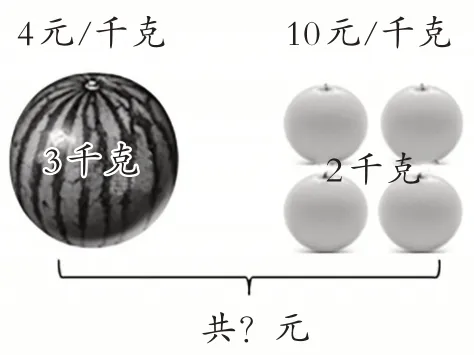
师：就差“一共需要花多少钱”了，现在能解决这个问题了吗？

生：能，4×3+10×2=32（元）。

（教师顺着学生的回答，板书算式）

师：能读懂他的想法吗？这个综合算式是什么意思，你是怎么想的？

生：4×3求的是西瓜的价钱，10×2求的是橙子的价钱，把它们加起来就是买这些水果一共要花的总价钱。

师：原来这里有一个等量关系，你们发现了吗？

生：西瓜的总价+橙子的总价=水果的总价。

（教师板书：西瓜的总价+橙子的总价=水果的总价）

师：在现实生活中，问题情境有时是各种各样的。就这个情境来说，其他条件不变，如果把所求问题变为已知，你能把其中一个条件变成要解决的问题吗？比如（课件出示情境图）把西瓜的质量变为未知的问题，还能解决吗？

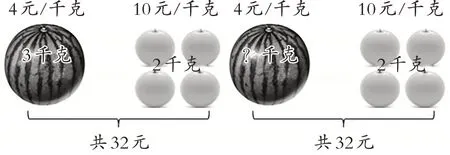
生：（32-10×2）÷4。

师：能读懂他的想法吗？

生：10×2求的是橙子的钱数，32-10×2就是用水果的总价钱减去橙子的钱数，得到的就是西瓜的钱数，（32-10×2）÷4 的意思是再用西瓜的钱数除以西瓜的单价，最后就等于西瓜的质量。

（学生解释得十分费力）

师：看来想要说清楚这个算式的想法还真是不容易。能不能尝试着用今天学习的方式（指黑板x+2=5、4y=2），把这里面的关系表示出来呢？

生：4x+10×2=32。

师：根据是什么呢？

生：西瓜的总价+橙子的总价=水果的总价。

师：（指黑板）还是这个等量关系。

【分析与思考】在解决“一共需要花多少钱”的问题时，学生根据以往经验自然使用算术法解决，在学生读懂“4×3+10×2=32”这个综合算式后，教师启发学生发现其中蕴藏的等量关系。接下来，在同一个情境中，教师将所求问题变为已知，将其中一个条件变成要解决的问题后再让学生尝试解决，学生根据条件和信息逆向思考，即用算术思维“费力”解释想法。在这个过程中，教师启发学生用设有字母的等量关系式来简明地表达和解释上述问题解决的思路，使学生进一步感悟代数思维与算术思维顺向与逆向思考的本质区别，体会代数思维的意义，经历方程建模的初步过程。

师：现在看看（指黑板x+2=5、4y=2、4x+10×2=32），这样的式子叫什么？

生：方程。

师：那请你说说什么是方程呢？

生：方程里要有未知数，还要是等式。

生：方程就是含有未知数的等式。

生：我觉得方程表达的是一种等量关系。你看，“x+2=5”表达的是“西瓜的质量+2 千克=5 千克”这个关系，“4y=2”表达的是“1 个橙子的质量×4=2 千克”这个关系，而“4x+10×2=32”表达的是“西瓜的总价+橙子的总价=水果的总价”这个关系。

生：我同意他的观点，等量关系用方程的形式表达起来显得更简洁。

【分析与思考】无论学前还是学后，学生在解决问题时更多地习惯于停留在或依托于算术思维上，对方程无认同感或亲近感，这是教师必须直面的现实困境。既然现实中学生的思维习惯是这样的，那么我们不妨顺应学生的想法，不回避算术法，引导学生在问题解决的背景下体会方程思想的本质和价值，经历数学建模的过程，建立方程的概念，初步认识方程的意义——方程表达的是具体问题情境中量与量之间的一种等量关系，找到这种等量关系能够帮助学生以顺向思考的方式清晰简洁地解释问题解决的思路。

二、经历建模，认识本质，初悟价值

（教师出示情境图）

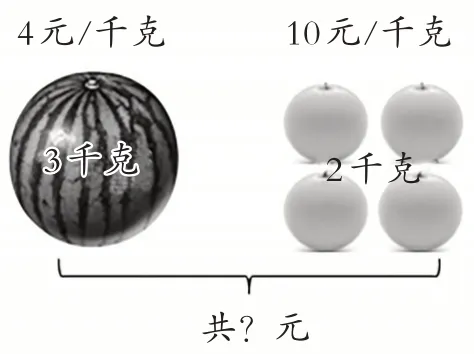
师：还是这个情境，刚才我们变换了条件和问题，把西瓜的质量当问题，可以列算式解决，也可以列方程解决。你能否再转换条件，把已知信息变成问题，然后尝试着列方程来解决？

（学生在学习单上试做，教师巡视指导，了解情况。之后，展示一位学生的想法，全班交流）

生：我把西瓜的单价变为问题，于是就把“4 元/千克”假设成不知道，变成“？”。然后，设为x元/千克，这样列出的方程就是3x+2×10=32。

生：你的这个方程是根据什么列出来的？

生：（指板书“西瓜的总价+橙子的总价=水果的总价”）我是根据这个等量关系列的，后面是解法。

师：解这样的方程，我们还没学。这位同学能列出方程并正确解答，请大家把掌声送给他。

生：我列出了2 个方程。我是把橙子的质量看成问题，然后设为a千克，这样列出的第一个方程就是10a+4×3=32。第二个方程是把橙子的单价看成问题，设为y元/千克，根据等量关系就列出了2y+3×4=32。

生：我发现你列的方程里的未知数有“a”还有“y”，并没有“x”。以前我以为方程里的未知数只能用“x”表示，看来任何一个字母都能表示。

生：不光字母，其他的符号也行，比如前面那个方程4x+10×2=32 还可以列成4c+10×2=32，4□+10×2=32。

师：你们的探讨很有意义。（指着“3x+2×10=32，10a+4×3=32，2y+3×4=32、4x+10×2=32”）四个方程仔细观察，你还有什么发现？

生：我发现这些方程虽然长得都不一样，但是它们的根据都是一样的，都是“西瓜的总价+橙子的总价=水果的总价”这个等量关系。

生：的确是这样，同一个等量关系解决了好几个问题。

师：你对方程有什么感受？

生：一个等量关系就能解决很多问题。

生：同一个等量关系列出了不同的方程，解决了不同的问题。

生：方程实际上就是一种等量关系，列方程找准等量关系很重要。

【分析与思考】教师沿着上述主题情境拾级而上，启发学生在自主变换条件和问题后尝试列方程解决，感受同一个等量关系可以解决同一个情境中不同的问题。在对比中学生发现，同一个等量关系可以列出不同的方程来解决不同的问题。在方程建模的过程中，学生再次认识到“方程表达的是等量关系”的本质，在“同”与“不同”中感悟到了方程的独特价值。

三、再次建模，体会本质，深化认识

师：看来等量关系真的很重要。这里的“西瓜的总价+橙子的总价=水果的总价”好像就是“部分量+部分量=总量”，这个关系在下面这个情境里你还能找到吗？（出示情境图）

生：2个热水瓶的水量+1个水杯的水量=一壶水的量。

生：2个热水瓶的水量+200毫升=2000毫升。

生：1个热水瓶的水量×2+200毫升=2000毫升。

师：你能据此也列出一个方程吗？

生：2x+200=2000。

生：200+2m=2000。

生：2y=2000-200。

师：看看大家列出的这些方程，你有什么发现？

生：这些方程长得不一样。

生：这些方程都是依据同一个等量关系列出来的。

师：的确是这样。以2x+200=2000 为例，这个方程表达的还是“部分量+部分量=总量”的关系。那你还能据此给这个方程再编一个故事吗？

（学生先独立思考，再在小组内交流想法）

生：妈妈买了两瓶同样净含量的洗洁精，每瓶外加100 克的小袋优惠装，一共重2000 克。每瓶洗洁精重多少克？

生：爸爸坚持锻炼，每天跑相同的距离，跑了2天后如果再跑200 米就正好到2000 米了。爸爸每天跑多少米？

生：我和爸爸去商场，买了2 个同样的车载净化器，付给收银员2000 元，找回200 元。每个车载净化器多少元？

生：我觉得最后这位同学讲的故事有点儿问题。按照他所讲，每个车载净化器应该是900 元，2 个应该是1800 元，那直接付1800 元不就行了吗，干吗要付2000元再找回200？

师：这个质疑很有意思。看来用方程讲故事还不能随便讲，还要符合生活实际，要符合常理才行。

师：你对方程又有了哪些新的认识？

生：同一个方程能编出好多不同的故事。

生：一个方程能解决许多不同的实际问题。

生：刚才大家编出的这些问题，都可以用同一个方程来表示。

【分析与思考】这个活动中，教师主要是引导学生将前一个情境中的等量关系延伸概括为“部分量+部分量=总量”，再根据这个总括的等量关系在新的情境中寻找出新的等量关系并列出方程，进而体会不同形式的方程其实表达的都是同一个等量关系。接着，教师引导学生再次根据这个等量关系给方程“编”故事，让方程回归现实生活，启发学生再次经历数学建模过程，感受同一个等量关系可以解决不同情境中的不同问题，体会方程所承载的独特价值，感悟代数思维的妙处，深化对方程核心本质的认识，发展模型思想。