山地冰川中流线自动提取方法研究
张一新, 周建民, 桑文刚, 李 震, 黄 磊, 鲁安新
(1. 山东建筑大学 测绘地理信息学院,山东 济南 250101; 2. 可持续发展大数据国际研究中心,北京 100094;3. 中国科学院 空天信息创新研究院 数字地球重点实验室,北京 100094)
0 引言
冰川是气候条件与地形条件相结合的产物,是气候变化的指示器,对气候变化具有重要的反馈作用[1-2]。根据第二次冰川编目,中国是世界上中低纬度地区山地冰川最丰富的国家,共有冰川48 571条,面积约5.18×104km2[3]。冰川在自身重力的作用下会由高海拔区域向低海拔方向运动进而形成冰川冰流[4],冰川冰的最大流量轨迹称为冰川主流线[5]。当前,冰川主流线的提取方法是利用水文分析通过计算汇水线来实现,然而该方法计算的汇水线在地形平坦地区无法追索到冰川顶端边界[6]。因此,学者们提出了一种利用冰川中流线替代冰川主流线的提取方法[7-8],冰川中流线是冰川主流线的中心线[5],是反映冰川几何形态的重要参数之一,在测量冰川长度随时间变化[9]、分析冰川运动速度变化特征[10-11]、估算冰川体积[12]及构建一维冰川模型等应用中都有着重要的意义[13]。
近年来国内外学者针对冰川中流线的提取开展了大量的研究工作[5],一些自动与半自动的提取方法也被陆续提出来。Le Bris等[7]率先将冰川轴线引入到冰川中流线提取研究中,通过连接不同高程带等高线中点的方式获得冰川中心线实现冰川中流线的提取,但该方法只能提取单一中心线,且对于面积较大、形状复杂的冰川其提取结果并不一定为主冰流的中心线。Machguth等[8]提出了一种结合冰川表面宽度和坡度的冰川中流线提取方法,其成功率达到了95%~98%,但该方法需要较多的人工参与,进行模型参数的调整,对于数字高程模型数据也有较高的质量要求,且无法提取冰川支流的中心线。Kienholz等[14]将成本距离思想引入到冰川中流线提取过程中,利用欧式距离和高程对冰川中流线进行约束从而提高结果的准确性,该方法弥补了多分支冰川只生成单一中心线的缺点,但算法过程复杂,参数较多,且部分冰川中流线仍需要人工调整。姚晓军等[15]在GIS软件的支持下提出了针对单一盆地与单一出口、复式盆地与单一出口、冰帽三种类型冰川中流线的自动提取方案,其优化方案使提取结果更加合理,但该方法仅实现了对单一盆地与单一出口类型冰川中流线的自动提取,对于复式盆地与单一出口和冰帽类型的冰川中流线的提取仍需要专家知识的辅助,未实现完全自动化处理。杨佰义等[6]综合利用冰川中心线法和冰川主流线法获取了冰川长度线,在一定程度上提高了结果的准确性,但对于大面积冰川,由于受到地形起伏和数字高程模型数据质量的影响,使得获取的冰川长度线无法从海拔最高点流向最低点,需要人工进行修正。Ji 等[16]在ArcGIS 环境下利用Le Bris 和Pual 提出的方法,结合数字高程模型数据和冰川矢量边界线数据实现了冰川中流线的提取,然而该研究在高程最值选取等过程仍需要人工参与。Zhang 等[5]基于欧几里得分配和冰川表面地形特征,在ArcGIS环境下实现了对冰川中流线的自动提取,但该模型结构复杂,对于部分多出口坡面冰川和未分割的单一出口冰川的提取效果不理想,致使所得的冰川长度不准确。Hansen 等[17]通过计算数字高程模型数据的局部线性回归梯度下降来提取冰川中流线,利用组合对应于不同窗口大小的冰川中流线来提高结果的准确性,但是,此方法计算过程较为复杂且对于冰川中流线的提取仍需要人工提供初始点,而未完全实现自动化。
鉴于此,本文提出了基于泰森多边形法的山地冰川中流线自动提取方法,该方法以冰川编目数据中的冰川矢量边界线数据与数字高程模型数据作为输入,通过泰森多边形法生成冰川中心线,然后对中心线进行筛选从而获得冰川中流线。本方法在无需人工参与的情况下,不仅实现了对冰川中流线的自动化快速提取,还能准确地对冰川各支流的中流线进行提取,解决了基于冰川轴线方法只能提取单一中心线的问题,提高了冰川中流线提取效率。
1 方法介绍
本文所用到的核心算法是泰森多边形法、最短距离公式和Dijkstra 算法,利用泰森多边形法生成冰川内部的中心线作为相应冰川中流线的预选线段并使用最短距离公式对具有多起始点的中心线进行筛选,删除多余起始点,然后使用Dijkstra 算法沿冰川内部中心线进行最短路径选择,完成冰川中流线的提取。
1.1 泰森多边形法
泰森多边形又称为Voronio图或Dirichlet图,最初是由俄国数学家Georgy Fedoseevich Voronio 提出的一种关于空间邻近的算法,并在1900年由荷兰科学家A. H. Thiesseny 引入到降雨量的空间分析中,并将该方法正式称为泰森多边形法。该方法实质上是对空间平面的划分,即泰森多边形内的点至相应离散点的距离最近且位于泰森多边形上的点至其两边离散点的距离相等[18-19]。泰森多边形的性质使该方法在图像几何、计算机图形处理、计算机视觉等领域有着广泛的应用,同时随着对泰森多边形法研究的逐渐深入,也使其成为解决空间分析问题的重要方法[20-22]。
在众多应用领域中,泰森多边形法的主要功能之一便是利用泰森多边形的性质来提取地理实体的中心线,并将该中心线作为地理实体的抽象以近似表示该实体[23]。在构建泰森多边形的过程中,算法首先会提取地理实体边界线上的点作为离散点,根据离散点构建泰森多边形并对生成的泰森多边形的边进行筛选,只保留位于地理实体内部的部分作为该实体的抽象表示。
1.2 最短距离公式
由于本文需要对冰川所有中流线进行提取,因此需要确定每条冰川中流线的起始点。本文对冰川中流线起始点的确定主要分为两步:(1)沿冰川矢量边界线结合数字高程模型数据提取边界线上各折点的高程,并获取该边界线上高程最高点与最低点。(2)将边界线上的折点与边界线上邻近折点(每个方向取20个邻近点)的高程进行比较,若该折点高程高于所有邻近折点,同时大于相应冰川边界线上各折点高程分布的三分之一,则该点即为当前冰川中流线的起始点。由于冰川起始点通常位于高海拔地区,采用每个冰川三分之一高度作为阈值,降低了提取的冰川中流线起始于地势低洼地区的可能性,同时邻近点的选取也保证了所提取的起始点即为局部高程最值点。
然而,部分冰川中流线存在多个起始点的问题,为了解决该问题,本文引入了最短距离公式对上述过程提取到的冰川中流线起始点进行筛选[14],具体计算公式如下:
式中:r为两起始点间最短距离(m);S为冰川面积(m2);q1、q2分别为方程的两个参数,其值如表1所示。

表1 各参数值和单位Table 1 Parameter values and units
如果范围r中有多个起始点,方法只保留高程最高的起始点并删除其余起始点,同时方法限定r的取值范围最小为500 m。
1.3 Dijkstra算法
本文方法提取的冰川中流线结果是利用Dijkstra 算法搜索起始点与终点间距离最短的连线即最短路径实现的。Dijkstra 算法是目前广泛应用的求解最短路径算法之一,它是由荷兰科学家E.D.Dijkstra 提出的一种典型的单源最短路径算法。算法采用贪心算法的策略,通过计算起始点至终点不同路径下的权重,筛选出权重值最小的路线作为两点间的最短路径[24]。
Dijkstra算法的基本思想如下:对任意一个带权无向图,取S 为顶点集合,P 为各点间权重的集合,以两点间连线的距离作为权重,若两点间无直线连接则将权重设为无穷大。在算法开始时将顶点集合分为两部分,第一部分为S1代表已求出最短路径的顶点,此时该部分仅包含起始点,在之后每求得一个最短路径便将对应顶点放入该数组中,直到所有顶点遍历完毕。第二部分为S2代表待确定最短路径顶点集,算法将遍历起始点的所有邻近顶点并从集合P 中查询两点间权重值,筛选权重值最小的连线作为当前顶点的最短路径,并将该顶点存储至S1中,当S2中顶点遍历完成后,集合S1中的所有顶点的连线即为起始点至目标点间的最短路径。
2 应用研究
2.1 研究区域与数据源
青藏高原及周边地区的平均海拔超过4 000 m,是除南极和北极以外冰川最为发育的地区,
冰川面积约为9.8×104km2,也是中国境内山地冰川最丰富的地区[25-26]。因此,本文选择青藏高原东南部地区作为研究区域,该区域内广泛分布有山地冰川1 014 条,冰川形状各异,且地形条件极其复杂[27],为本文方法进行山地冰川中流线的自动提取研究提供了优异的实验区域。
本文选择Randolph Glacier Inventory(RGI)v6.0 数据集作为研究区域的冰川数据源,该数据集是由美国国家冰雪数据中心负责管理和更新的全球范围的冰川编目数据集。RGI v6.0 数据集将青藏高原及其周边地区划分为了喜马拉雅地区、西藏南部和东部地区、横断山脉地区及昆仑山和祁连山地区等共计13个子区域[28],并分别记录了它们的面积、坡度和坡向等空间信息,为进行山地冰川中流线的自动提取研究提供了条件。
本文使用的数字高程模型是美国航天航空局(NASA)及地理信息情报局等联合提供的SRTM1(Shuttle Radar Topography Mission1)数字高程模型,该模型由美国航天飞机“奋进号”历时11天采集的60° N 到56° S 之间的所有高程数据组成[29-30],覆盖面积达1.19×108km2,占地球面积的80%。同时,由于其在地球大部分区域内具有统一的分辨率和精度而被广泛应用于各个研究领域[31]。相较于ASTER DEM 等数字高程模型数据,SRTM1 数字高程模型有良好的垂直精度且该数据受坡度、土地利用类型及地貌等因素的影响小,保证了其即使在复杂的山地地区也能提供良好的高程数据[32-33]。
2.2 冰川中流线提取
本方法以冰川矢量边界线数据和数字高程模型数据作为输入,使用Python 作为基础编程语言架构山地冰川中流线自动提取模型,同时结合GDAL、Scipy、Shapely 等第三方空间数据处理库,实现对冰川矢量边界线数据和数字高程模型数据的读取、泰森多边形的构建、模型结果输出等功能。该模型的主要处理过程如图1所示。
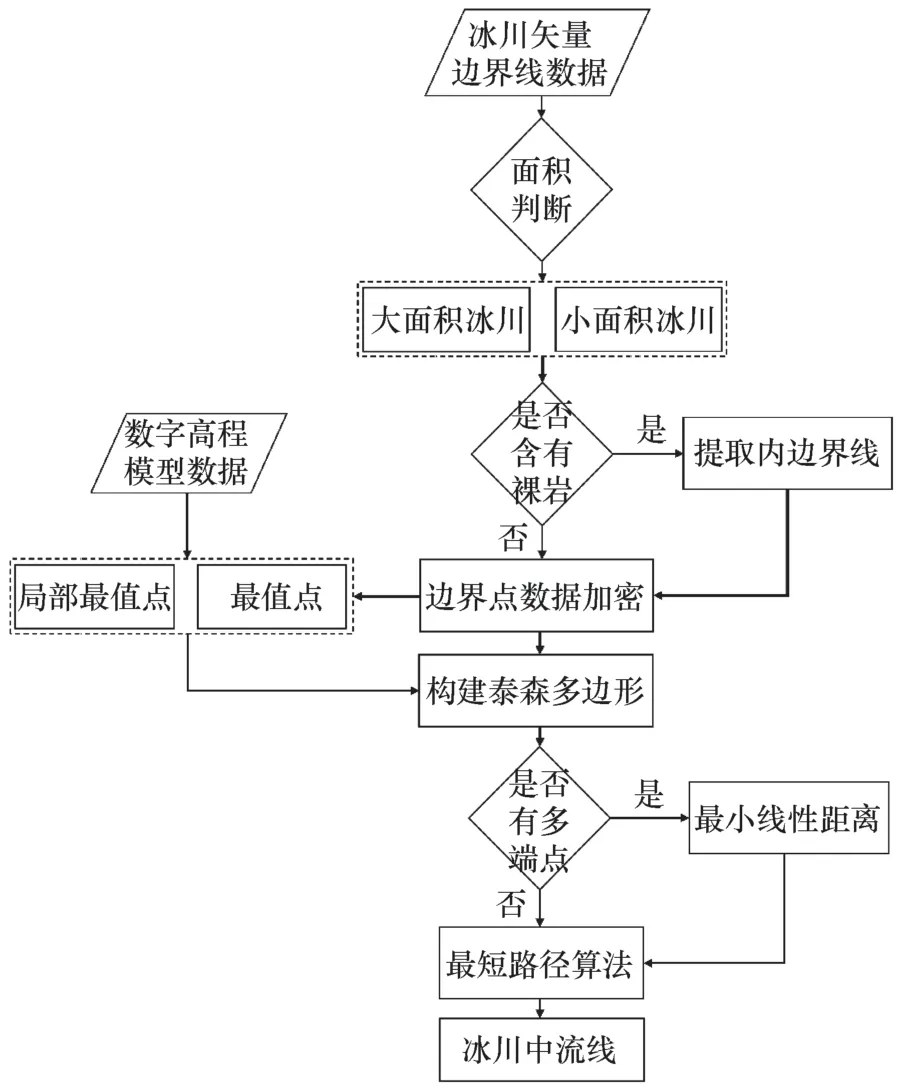
图1 冰川中流线提取技术流程Fig. 1 The technical process of glacier centerline extraction
泰森多边形法生成的冰川中流线与冰川矢量边界线上离散点采样密度有关,即随着离散点采样密度的增加,泰森多边形提取的中流线也会更加准确(图2),但是较高的采样密度会降低模型的运行效率。因此作为提取冰川中流线的第一步,模型首先会根据冰川外边界线判断冰川面积大小,并依据冰川面积采用经验参数对模型进行初始化。即对于大面积冰川(冰川面积大于5 km2),模型在构建泰森多边形时便采用100 m 的采样密度,而对于小面积冰川(冰川面积小于5 km2)则采用10 m 的采样密度以在保证准确性的前提下提高模型的运行效率。然而,由于部分冰川内存在裸岩区即内边界线,因此为了保证模型生成的冰川中流线不穿过裸岩区,模型会根据冰川矢量边界线数据对该冰川区域内是否存在裸岩区进行判断。当区域内无裸岩区时,模型只需要提取外边界线并对其进行加密,而当区域内存在裸岩区时,模型则需要同时提取内、外边界线并对其进行加密以保证结果满足冰川中流线不穿过裸岩区的绘制原则。冰川矢量边界线数据处理结果如图3所示。
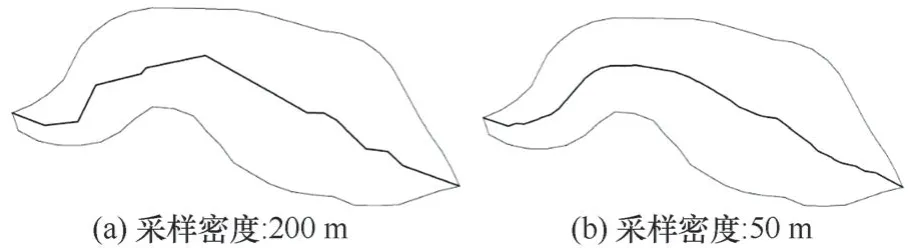
图2 不同采样密度下泰森多边形法提取的冰川中流线Fig. 2 Glacier centerlines extracted by Thiessen polygon method with different sampling densities (200 m and 50 m)
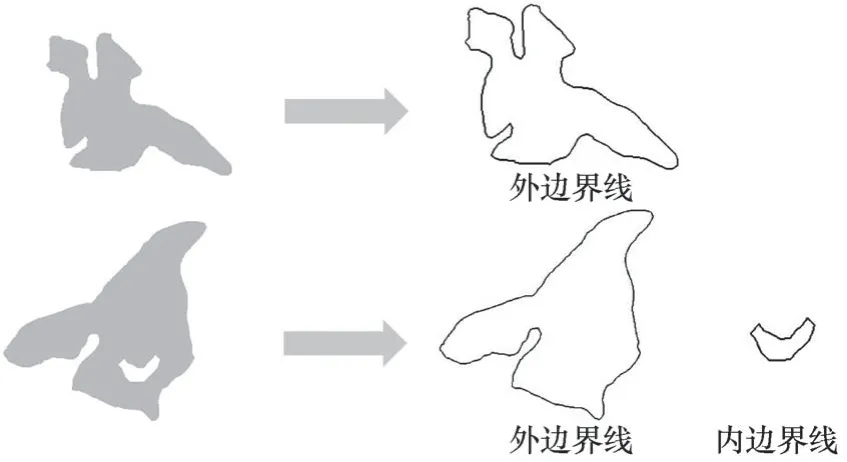
图3 冰川矢量边界线的提取Fig. 3 The extraction of glacier outlines
当冰川矢量边界线加密完成后,模型便引入数字高程模型数据沿加密后冰川外边界线上各点获取高程值,再依据1.2 节中的步骤选取高程同时满足大于其附近点高程并大于相应冰川边界线上各点高程分布的三分之一的点作为冰川中流线的起始点,结果如图4所示。同时,以加密后外边界线上的点作为离散点绘制泰森多边形,结果如图5(a)所示,由于位于冰川外部的泰森多边形的边无法应用于冰川中流线的提取,所以我们只保留位于冰川内部的边作为冰川中流线的预选线段,结果如图5(b)所示。然后利用最短距离公式,根据冰川面积计算冰川中流线起始点间的最短距离,若最短距离内存在多个起始点,则需根据数字高程模型数据提取各起始点高程并进行比较,保留高程最高的起始点。
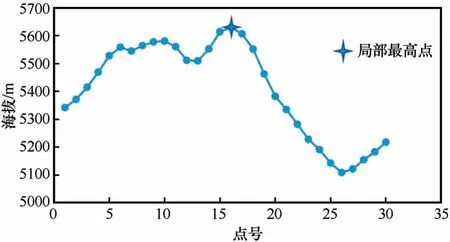
图4 局部最高点Fig. 4 The local highest point
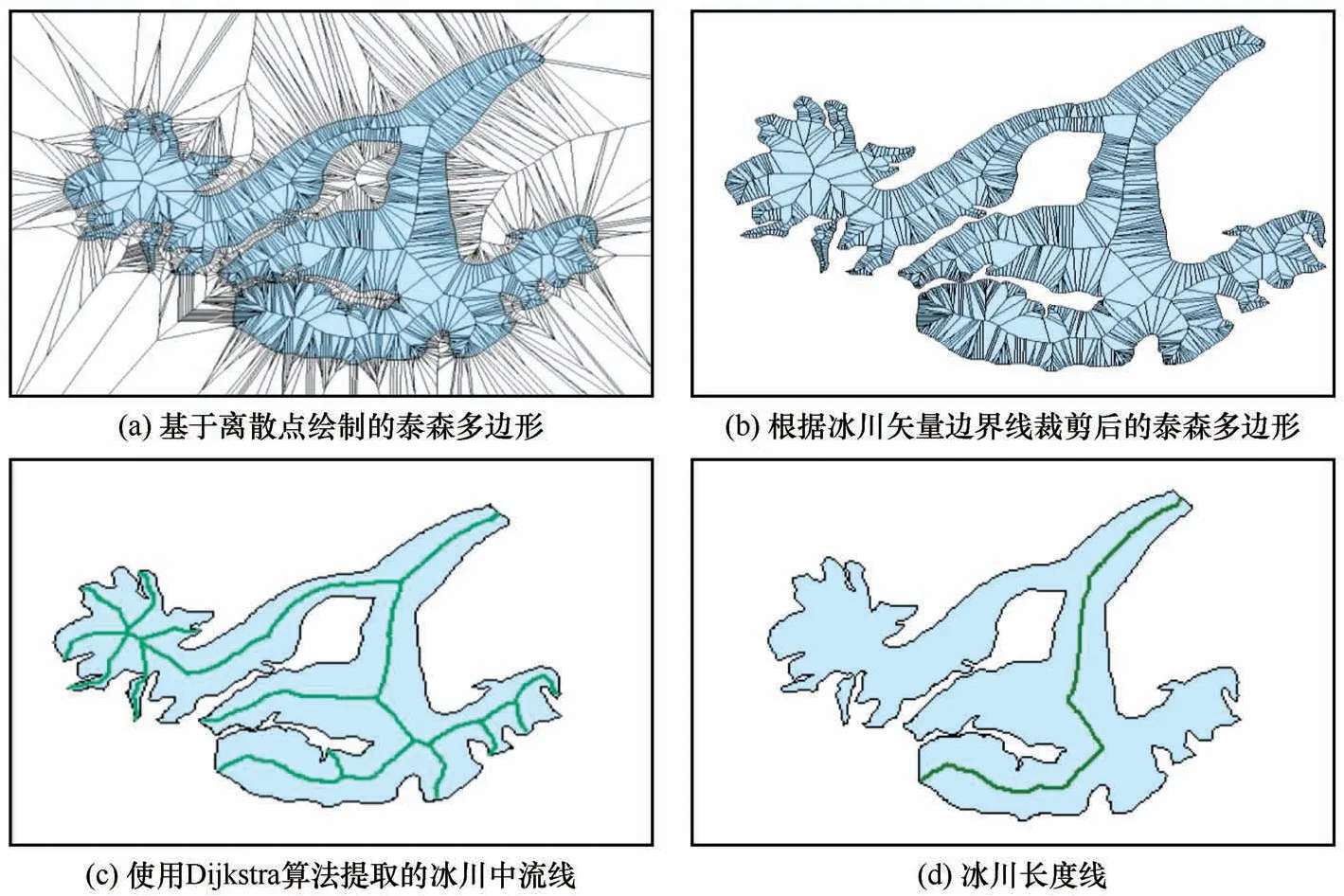
图5 利用泰森多边形法提取冰川中流线Fig. 5 Extraction of glacier centerlines by Thiessen polygon method: voronoi diagram based on scattered points (a),voronoi polygons clipped by glacier vector boundary lines (b), glacier centerlines extracted using Dijkstra (c), and glacier length line (d)
在完成冰川中流线多起始点处理后,模型便使用Dijkstra 算法以各中流线起始点与其邻居顶点之间连线的距离作为该直线的权重计算起始点到终点之间的最短路径,完成所有中流线的选取工作,结果如图5(c)所示。最后,选择最长冰川中流线作为冰川长度线以近似计算该冰川长度[6],选取结果图5(d)所示。
3 应用评价
对冰川中流线提取精度进行评估最准确的方法是将提取结果与实际冰川中流线进行比较,然而,由于山地冰川地处偏远山区,很多冰川人力无法到达,因此很难实测冰川的真实中流线。但是为了对本文所提方法进行精度评估,我们选择采用与其他冰川中流线提取方法提取结果进行对比的策略,以评估本文方法的可靠性和有效性。
在现有的研究中,Kienholz 等[14]提出的方法同样采用了冰川矢量边界线数据和数字高程模型数据作为输入,为两方法间同数据源的对比分析提供了条件。本文通过计算平均长度和长度比对两方法的提取结果进行了初步的比较。由表2 可以看出,利用Kienholz 等[14]的方法计算得到的冰川平均长度为3.156 km,使用本文方法计算得到的冰川平均长度为3.13 km,两种方法的平均吻合长度为3.11 km 约占总长度的99.4%,两种方法所提取到的冰川长度平均值几乎相同。为了便于表述,本文将Kienholz等[14]提出的方法定义为Kienholz方法。

表2 本研究计算的长度与Kienholz等[14]的比较Table 2 Comparison between the length calculated in this study and Kienholz et al[14]
为了进一步比较两方法的提取结果,本文引入了冰川长度比Ra/k用以评价本文使用的泰森多边形法提取结果与使用Kienholz 方法提取结果的优劣。具体计算公式如下:
式中:La为本文方法所提取的冰川长度;Lk为Kienholz 方法得到的冰川长度。由表2 可知两种方法的长度比平均值为0.98,表明两种方法之间存在较小的负向偏差。
本文根据冰川面积将研究区域划分为0.1~0.5 km2、0.5~2.5 km2、2.5~10 km2及大于10 km2四组并分别计算两方法的长度比,以比较两方法对不同面积冰川的提取结果,计算结果如图6 所示。结果表明,共有90.2%的数据长度比分布在0.9~1.1之间,4.4%的数据长度比大于1.1,5.4%的数据长度比低于0.9。离散较大的数据多集中于小面积冰川中,当冰川面积大于0.5 km2时两方法的长度比值向1收敛。造成两种方法长度比数据离散的原因与冰川长度的不确定性有关,在通常情况下小面积冰川的不确定性约为20%,大面积冰川的不确定性约为15%,且随着数字高程模型数据质量的提高而逐渐降低[8]。
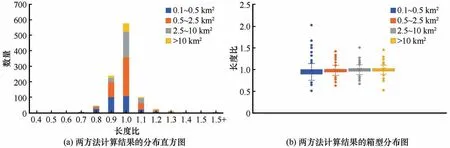
图6 不同面积冰川长度比Fig. 6 Length ratio of glaciers of different areas: histogram of calculated results for both methods (a),box plot of calculated results for both methods (b)
通过两方法冰川长度对比结果可知,两种方法所提取到的冰川平均吻合长度达到了总长度的99.4%,表明两方法提取的冰川平均长度几乎相同,而对于不同面积的冰川,本文分别提取了其冰川长度并与Kienholz 方法提取的相应长度进行比较,计算的长度比平均值达到了0.98,与完全一致(Ra/k=1)相差较小。整体而言,两种方法所提取到的冰川长度具有很高的一致性,表明本文方法提取的冰川长度具有可靠性和有效性。
对于不同类型冰川的中流线提取,本文又引入了Zhang 等[5]的方法与本文方法和Kienholz 方法的提取结果进行对比,结果如图7所示,同时为了便于表述本文定义Zhang等[5]的研究方法为Zhang方法。从图中可以看出对于不同类型的冰川,各方法对冰川中流线的提取结果有一定的差异。对于结构较为简单的单式山谷冰川,本文方法的提取结果与Kienholz 方法和Zhang 方法的提取结果差异较小,对于结构较为复杂的复式山谷冰川和坡面冰川,本文方法所提取到的冰川中流线数量多于Kienholz方法但少于Zhang方法,而对于冰帽类型冰川,本文方法所提取到的冰川中流线数量均多于Kienholz方法和Zhang 方法的提取结果。图8 显示了本文方法与Kienholz方法对研究区域内冰川中流线的提取结果对比,由图8 可以发现,本文方法提取出了Kienholz方法所没有提取的冰川支流的中流线,如方框区所示,表明较之Kienholz 方法本文方法提取结果覆盖更全。
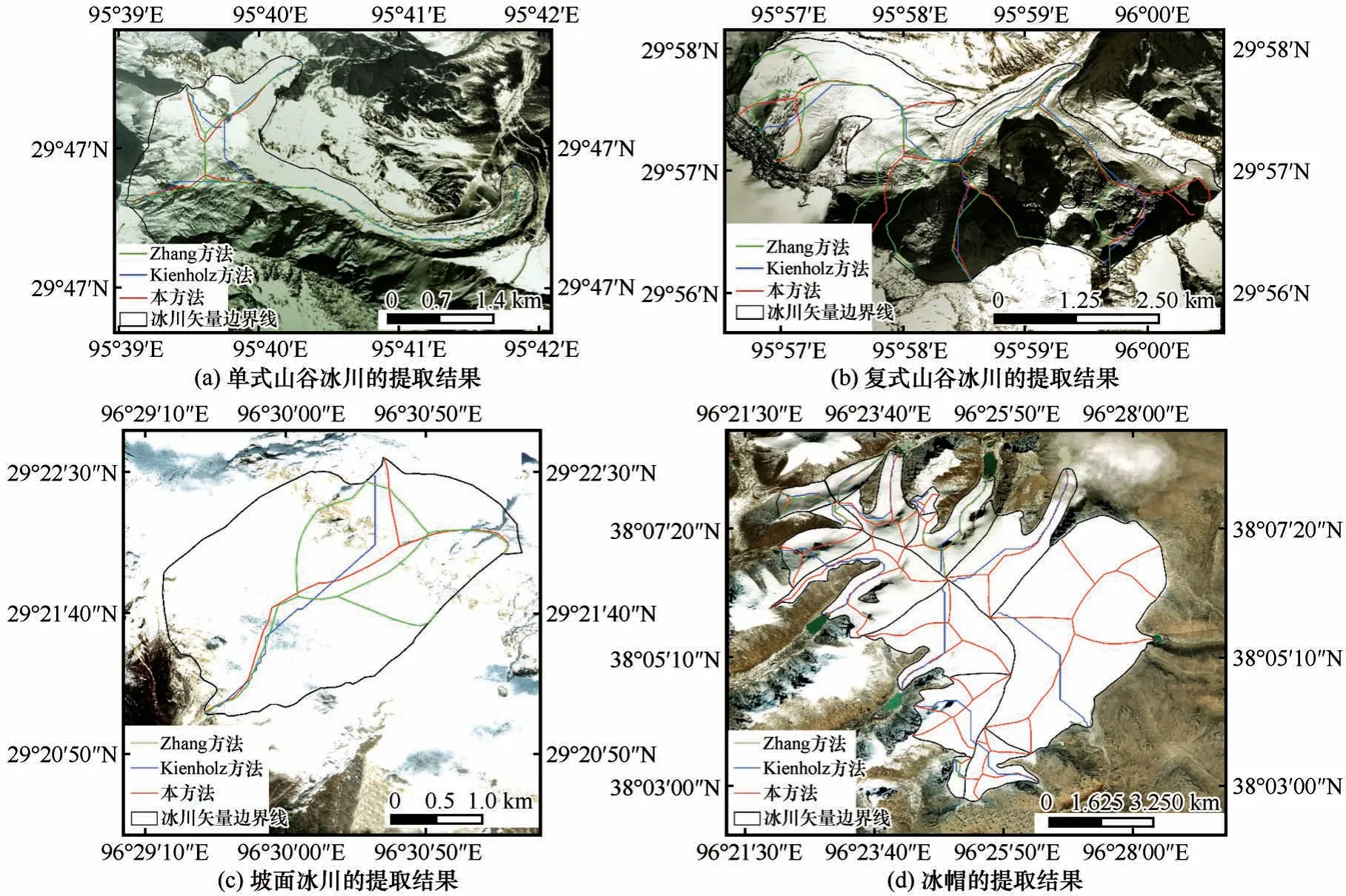
图7 三方法提取结果对比Fig. 7 Comparison of extraction results of three methods, the extraction results of single-type valley glaciers (a),compound-type valley glaciers (b), slope-type glaciers (c), and ice caps (d)
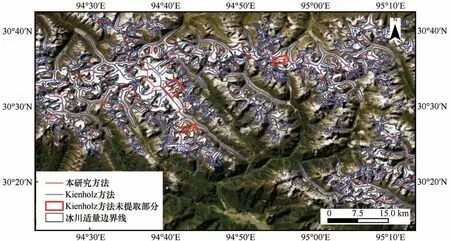
图8 两方法冰川中流线提取结果Fig. 8 The glacier centerline extraction results of two methods
4 讨论与结论
本文提出了一种基于泰森多边形法的山地冰川中流线自动提取方法,该方法结合冰川编目数据中的冰川矢量边界线数据和冰川区数字高程模型数据,通过计算最低点和局部最高点,利用泰森多边形法提取研究区域内所有冰川中心线,并使用Dijkstra 算法得到冰川中流线。解决了基于冰川轴线方法进行多支流冰川中流线提取过程中只能提取单一中流线的问题,在无人工参与的情况下,实现了山地冰川中流线的自动化快速提取。通过对青藏高原研究区内1 014 条山地冰川进行的中流线提取实验,本方法共提取了冰川中流线2 114 条,平均长度为3.13 km。通过与现有方法的提取结果进行对比分析,本文方法通过自动化的提取模型获得的冰川长度与现有方法具有很高的一致性,且本文方法提取的冰川中流线结果覆盖更全。
然而本文方法在实际应用过程中依然存在着部分缺陷。比如,本方法对于冰川矢量边界线上离散点采样密度的选取依然采用经验参数,这导致了在形状复杂冰川的中流线提取过程中部分局部最高点无法有效识别。同时,与现行的通用自动化冰川中流线提取算法相同,本文算法在对多出口类型冰川中流线提取过程中同样以冰川矢量边界线上最低点作为冰川出口,这可能会导致所提取到的冰川中流线长度出现偏差等问题。本文提出的冰川中流线提取算法,需要以冰川矢量边界线数据作为输入。但由于该输入数据自身存在部分误差,导致冰川中流线提取结果受到影响,像RGI v6.0 冰川编目数据中部分冰川矢量边界线呈现锯齿状形态,这会使得基于冰川矢量边界线提取的冰川局部最高点和最低点出现误差,同时锯齿状的冰川矢量边界线也会使本文方法提取的冰川中流线出现明显的偏折。
针对上述的缺陷,在后续研究工作中可以采取以下方法提高提取结果的精度:(1)根据冰川类型和复杂程度进一步完善冰川矢量边界线上离散点采样密度及局部最高点和最低点的选取方法,以提高方法的适用性。(2)在提取冰川中流线的过程中加入辅助线将多出口类型冰川分割为单一起始点单一出口类型的冰川和多起始点单一出口类型的冰川,在降低其复杂程度的同时实现对多出口类型冰川中流线的提取。(3)在模型中加入预处理算法对存在锯齿形态的冰川矢量边界线进行平滑处理,以避免因锯齿状冰川矢量边界线导致的冰川中流线提取错误的问题。

