基于随机搜索算法和AdaBoost 模型预测LF 精炼过程脱硫率
严旭梅, 陈 超, 王 楠, 陈 敏
(东北大学1.多金属共生矿生态化冶金教育部重点实验室; 2.冶金学院, 沈阳 110819)
钢水中的硫是一种有害元素,会使钢在轧制过程中产生热脆现象[1].转炉或电炉冶炼阶段的脱硫效果较差,但随着用户对钢质量要求的不断提高,LF 精炼过程的脱硫任务变得越来越重要[2].轴承钢作为一种重要的特殊钢产品,其深脱硫工艺已成为国内外研究的重点[3].目前,已有文献从脱硫机理角度构造了许多经验公式和回归模型[4-5],用以控制冶金过程中的脱硫效果.但该过程的脱硫机理极其复杂,因此这些模型均存在一定的应用局限性.近年来,机器学习算法在冶金领域被广泛应用[6-8].Ma 等[9]通过构造ANN 模型来预测精炼渣的脱硫能力,Xin 等[10]利用正则化的ELM模型预测了LF 精炼渣的脱硫能力.虽然这些模型均取得了一定的预测效果,但其使用的数据主要为实验数据,预测结果极易与实际结果产生偏差,且ANN 模型和正则化的ELM 模型均为单一模型.因此,为进一步提高模型的拟合与泛化能力,集成模型开始被广泛应用并取得了良好的效果[11-14].而LF 精炼过程的脱硫效果一直以来备受关注,但与脱硫率预测相关的文章却鲜见报道.
为了更精准地控制LF 精炼过程的脱硫效果,本文中对GCr15 轴承钢冶炼过程中电炉出钢、炉后脱氧合金化及LF 精炼3 个阶段的实际生产数据进行采集,并使用AdaBoost 模型对LF 精炼过程的脱硫率进行预测,旨在提高实际精炼过程的脱硫效果;比较分析网格搜索算法、随机搜索算法及贝叶斯优化算法对AdaBoost 模型超参数优化效果和优化时间的影响,并利用所采集的现场数据进行验证,以期通过结合随机搜索算法和AdaBoost 模型来实现对LF 精炼过程脱硫率的精准预测.
1 数据采集
本文中从某钢厂选取了859 条GCr15 轴承钢在LF 精炼过程中的实际生产数据,具体信息如表1 所列.根据冶金原理可知,精炼过程中的脱硫率主要与顶渣成分及精炼温度有关,而顶渣成分又主要与物料的加入情况相关.其中,转炉或电炉的出钢信息不仅会影响炉后脱氧合金化阶段的合金物料及造渣剂的加入情况,同时也影响着LF精炼过程的物料加入情况.因此,本文中采集的数据包括电炉出钢、炉后脱氧合金化和LF 精炼3 个冶炼阶段的主要参数信息.精炼过程中脱硫率的计算公式如式(1)所示,输入变量与脱硫率之间的皮尔逊相关系数如图1 所示.由图1 可知,电炉出钢阶段的碳含量(质量分数,下同),炉后脱氧合金化阶段的硅铁、高碳锰铁、低碳锰铁、石灰、化渣剂、铝块,LF 精炼阶段的石灰、碳化硅、硅铁、低钛低铝硅铁与脱硫率的皮尔逊相关系数的值均较高(绝对值均大于0.4).因此,脱硫率与脱氧剂、造渣剂的加入,以及出钢碳含量均密切相关(包含正相关和负相关),这也说明在实际冶炼过程中物料的加入对脱硫率的影响极其复杂.通过观察目标变量脱硫率可知,现场采集的平均脱硫率达到0.88,其中最小脱硫率为0.45,最大脱硫率为0.97,这表明实际生产中脱硫率的波动很大.因此,构建脱硫率预测模型来稳定LF 精炼过程的脱硫效果十分必要.
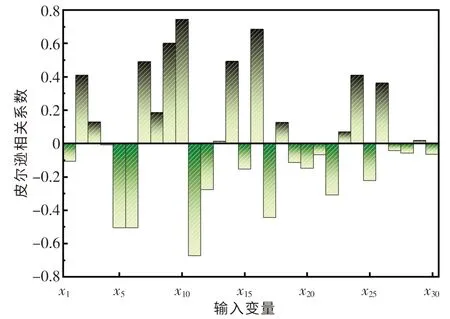
图1 输入变量x 与脱硫率变量y 的皮尔逊相关系数Fig.1 Pearson correlation coefficient between input variable and target variable
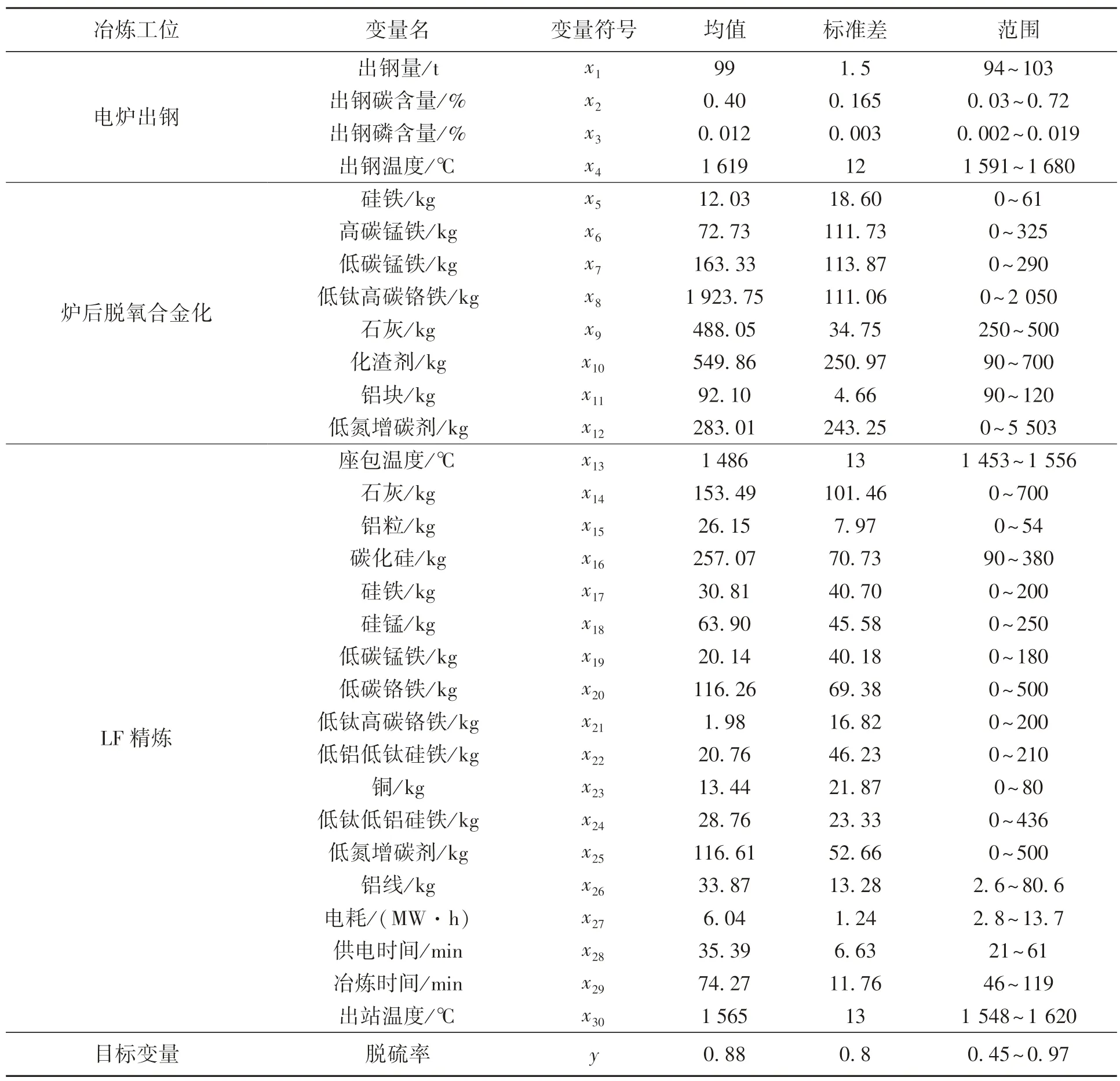
表1 采集变量数据统计信息表Table 1 Statistical of collected process parameter
式中:η代表脱硫率;w[S]0代表电炉出钢时钢水的初始硫含量;w[S]代表LF 精炼出站时钢水的硫含量.
2 模型建立
2.1 AdaBoost 模型
AdaBoost(adaptive boosting)模型是一种集成模型框架[15],基本原理如表2 所列.而分类回归树(CART)[16]模型具有较快的训练速度、更少的超参数及较好的拟合能力等特性[17],因此本文中采用的AdaBoost 模型是由CART 模型和AdaBoost模型组合而来的.

表2 AdaBoost 模型伪代码Table 2 Pseudocode of AdaBoost model
2.2 模型评估
本文中选用AdaBoost 模型对采集的数据进行建模.为了更好地评估结果,选用决定系数R2[式(2)]、平均绝对误差MAE[式(3)]、均方误差MSE[式(4)]、均方根误差RMSE[式(5)],以及5 折交叉验证(five-fold cross-validation)等进行评价.本文中所应用的所有机器学习模型都来自Python 的 scikit-learn 模 块[18], 运 行 环 境 为Windows10 操作系统,CPU 型号为Intel (R) Intel Xeon E5-2680 v2,内存为32G.
式中:n代表样本个数;yi代表LF 精炼过程中实际脱硫率代表LF 精炼过程中的预测脱硫率;代表LF 精炼过程中实际脱硫率的均值.
2.3 参数优化算法
(1)网格搜索(grid search,GS)算法.GS 算法是一种具有枚举遍历性质的搜索算法,其主要步骤如图2 所示[19].它的主要思想是先将模型中的超参数进行枚举并组合,然后采用遍历算法对每个组合进行K折交叉验证(K-fold crossvalidation)评估,最后通过对比评估值从所有超参数组合中选出最优超参数.
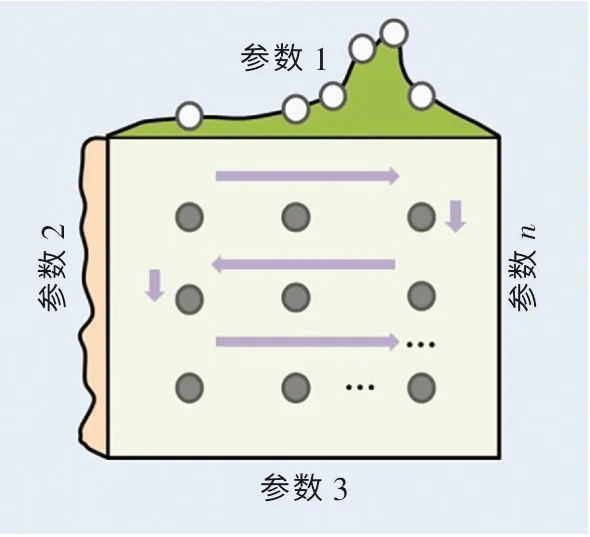
图2 网格搜索算法流程图Fig.2 Schematic diagram of grid search
(2)随机搜索(random search,RS)算法.对于高维空间超参数优化问题,RS 算法比GS 算法更高效[20].RS 算法的具体流程如图3 所示.从图中可以看出,与GS 算法不同,RS 算法并不是枚举出所有超参数的组合,而是随机地产生一些超参数点并进行组合.因此,在RS 算法中,组合点的排布是随机的、交错的和无重复的,这有效提高了算法的搜索效率.而对于一些函数来说,参数2 的变化对函数值的影响远小于参数1 对函数值的影响.因此,枚举遍历的优化算法可能会导致计算资源的浪费,但RS 算法能更加高效地得到较好的超参数.
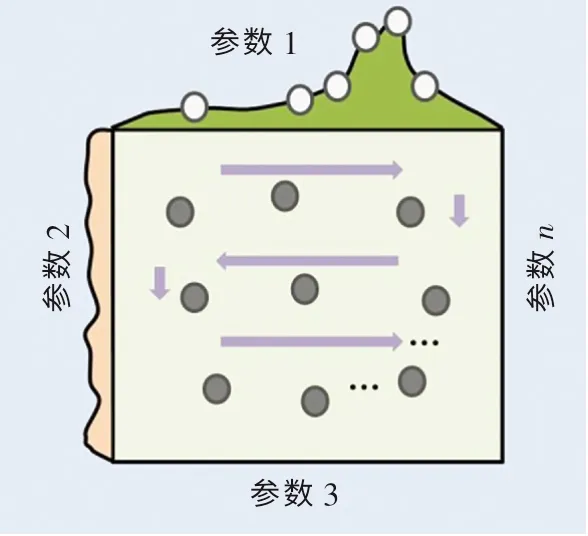
图3 随机搜索算法流程图Fig.3 Schematic diagram of random search
(3)贝叶斯优化算法(Bayesian optimization algorithm,BOA).BOA 算法是一种能够对复杂的黑箱函数进行全局寻优的高效优化算法框架[21-22].具体优化步骤如下所示.
步骤1:高斯过程.
高斯过程(Gaussian process,GP)[23]是BOA算法中最常用的概率代理模型.它[式(6)]主要由均值函数[式(7)]和协方差函数[式(8)]组成.
可用来计算高斯过程的协方差[24]函数有很多,如径向基函数(RBF)、平方指数协方差函数、Matérn 协方差函数等.如式(9)所示,由于Matérn(5/2)协方差函数有着更好的均衡性和稳定性[25],故本文中选取它作为高斯过程的核函数.
式中:r为x和x′的欧几里得距离,σ2为变量的方差.
选取n个初始点来计算高斯回归过程,将初始点{(x1,y1),…,(xn,yn)}的关系定义为
式中:y为目标函数,f(x)~N(u(x),k(x,x′)),ε为观察点x的噪声.通常假设噪声满足正态分布函数,即ε~N(0,σ2ε),y=f(x)+ε~N(u(x),k(x,x′)+σ2ε).
n个初始点与新点(xn+1,yn+1)的联合分布函数为
新点(xn+1,yn+1)的后验分布为
式中:u(xn+1)和σ2(xn+1)为所求的均值和方差.
步骤2:采集函数.
采集函数用于平衡贝叶斯优化算法的全局搜索和局部搜索能力, 主要包括EI (expected improvement),PI(probability of improvement) 和UCB(upper confidence bound),其中EI 最为简单和实用[21].本文中将EI 作为采集函数,可表达为
式中:Φ(.) 和φ(.) 分 别 为CDF (cumulative distribution function) 和PDF(probability density function).
表3 列出了利用贝叶斯优化算法优化AdaBoost 模型的具体步骤.

表3 贝叶斯优化算法伪代码Table 3 Pseudocode of the optimization process by BOA
2.4 优化效果对比
本文中介绍了3 种优化算法:GS 算法优化效果好,但所用优化时间较长;RS 算法的构建过程简单,且所需优化时间较短;BOA 算法虽具有较好的优化效果,但构建过程比较复杂.针对不同优化算法的特点,在R2和5 折交叉验证的评估下,本文中通过对比这3 种算法的优化效果和优化时间,选取出具有较好的脱硫率预测效果的AdaBoost 模型超参数优化算法.
根据scikit-learn 教程及相关参考文献[26],CART 模型选取max_depth 参数作为主要超参数.同时,基于CART 模型的AdaBoost 模型,其超参数主要为max_depth,n_estimators,learning_rate 和线性损失函数(见表4).表5 中列出了采用GS 算法对CART 模型和AdaBoost 模型进行优化的结果.由表5 可知,经GS 算法优化的AdaBoost 模型R2最大值为0.7,其拟合效果要优于采用scikitlearn 中默认超参数的AdaBoost 模型和优化后的CART 模型.这说明与CART 模型相比,AdaBoost模型具有更好的拟合和泛化能力,但其超参数需要相互协调才能达到最好的预测效果,否则其预测能力甚至可能会低于单一模型.

表4 AdaBoost 模型主要超参数Table 4 Main hyper-parameters of AdaBoost model
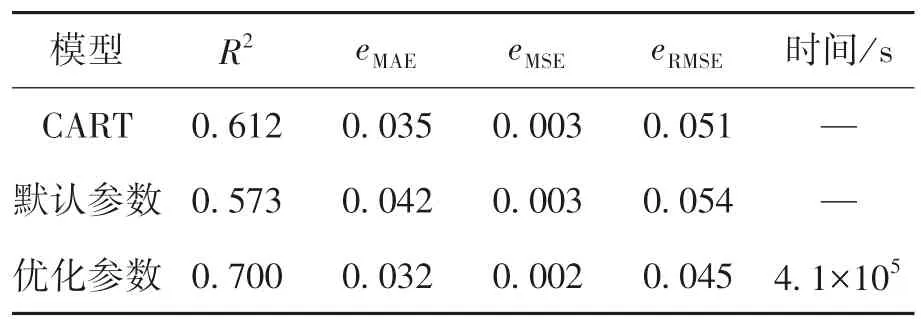
表5 网格搜索算法优化效果Table 5 Optimization results obtained by GS
由表5 还可知,利用GS 算法优化AdaBoost模型超参数需要消耗大量的优化时间.在CPU 10核心分配的条件下,所用时长约为41 万s.在实际应用中,这个优化时间是不切实际的.因此,本文中分别利用RS 算法和BOA 算法进行100,200,300,400,500 次迭代测试,优化AdaBoost 模型超参数.由于随机因素的干扰,对每组迭代测试均进行10 次实验,且计算过程中CPU 分配均为4 核心.图4 和图5 分别示出了RS 算法和BOA 算法的测试结果.可以发现,这两种算法的优化效果均会受随机因素的影响而产生一定的波动,故需要进行多次迭代测试才能够获得较好的优化效果.经多组迭代测试后,RS 算法优化AdaBoost 模型的R2最大值为0.694,BOA 算法优化AdaBoost 模型的R2最大值为0.695.表6 列出了RS 算法和BOA 算法每组迭代测试中10 次实验的均值.可以发现,对于AdaBoost 模型,这两种算法的优化效果基本一致,但在相同迭代次数下,BOA 算法所需的优化时间要大于RS 算法的优化时间.通过对比表5 和6 可知,虽然RS 算法和BOA 算法的优化效果要稍逊色于GS 算法,但这两种算法消耗的优化时间要远远小于GS 算法,故这两种算法更适合应用于实际中.同时,从本质上讲,RS 算法的时间复杂度为O(n),而以高斯过程为基础的BOA 算法的时间复杂度为O(n3), BOA 算法的构建过程比RS 算法更加复杂,需要更合理地选择采集函数、核函数等参数.因此,本文中选择RS算法来优化AdaBoost 模型的超参数.
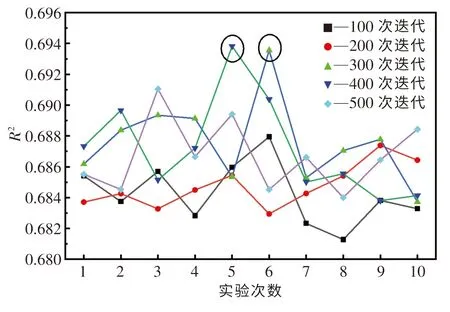
图4 RS 算法10 次优化实验结果Fig.4 Results of ten optimization tests for RS
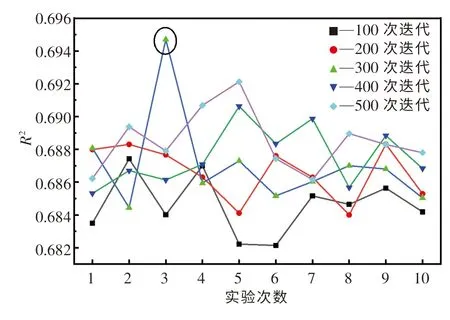
图5 BOA 算法10 次优化实验结果Fig.5 Results of ten optimization tests for BOA
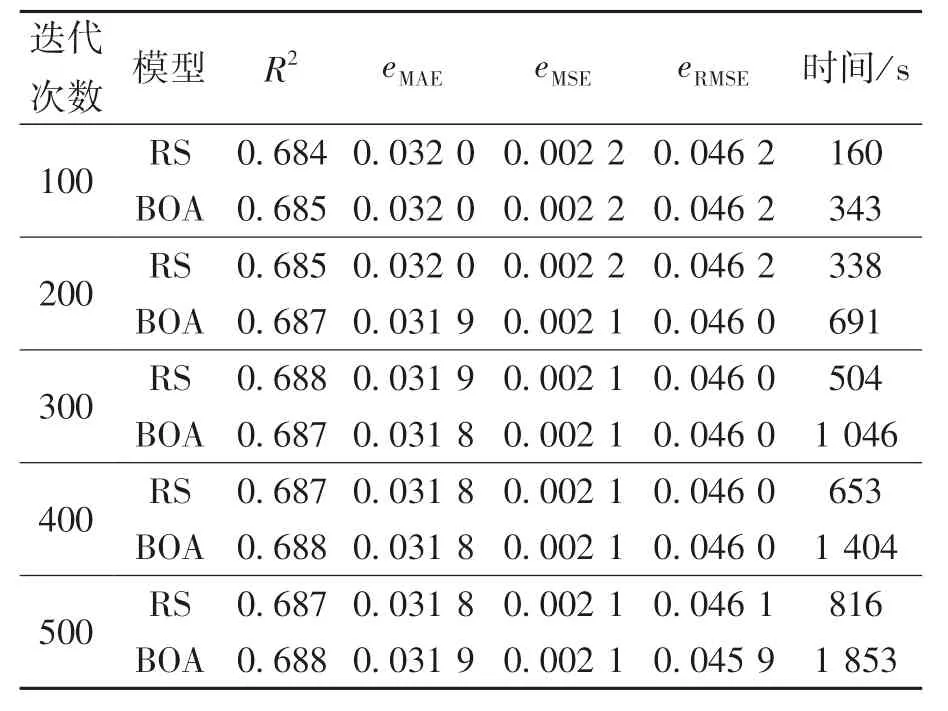
表6 RS 算法和BOA 算法的优化结果均值对比Table 6 Comparison of mean values obtained by RS and BOA
为了更好地测试RS 算法对AdaBoost 模型的优化能力,采用增加迭代次数的方式(1 000,1 500,2 500,3 000,4 000,5 000 次)对该算法的优化效果和优化时间进一步探索,并对每组迭代测试进行10 次实验,结果如图6 所示.由图可知,AdaBoost 模型的R2最大值为0.696.
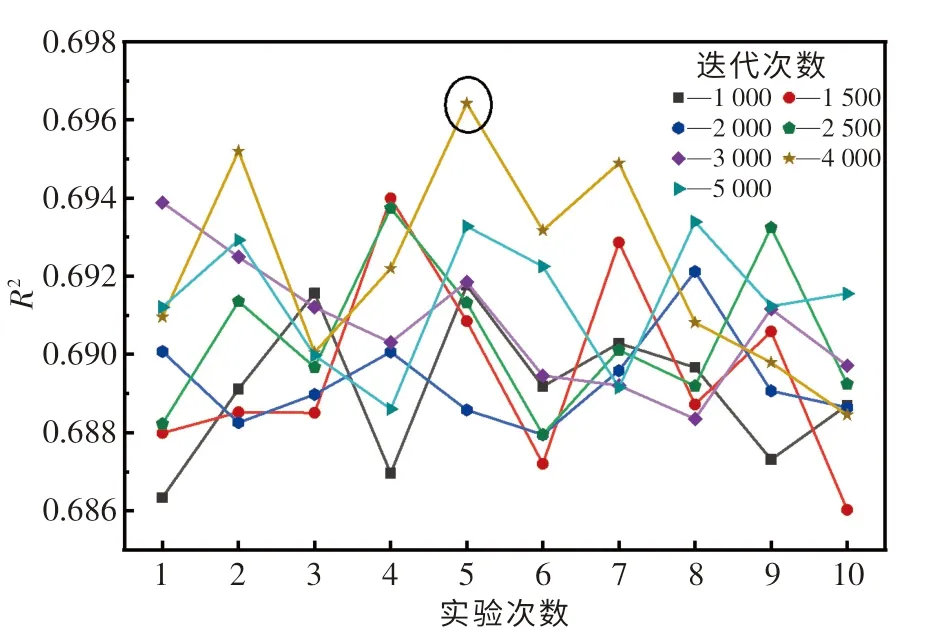
图6 RS 算法进一步优化Fig.6 Further optimization of RS
表7 列出了RS 算法每组迭代测试中10 次实验的均值.通过对比表6 和7 可知,RS 算法1 000次迭代所用的优化时间仍小于BOA 算法500 次迭代所用的优化时间,表7 中的优化效果要优于表6 中的优化效果(以R2为主要评估标准).综上可知,适当增加RS 算法的迭代次数,有利于提高该算法的优化效果.
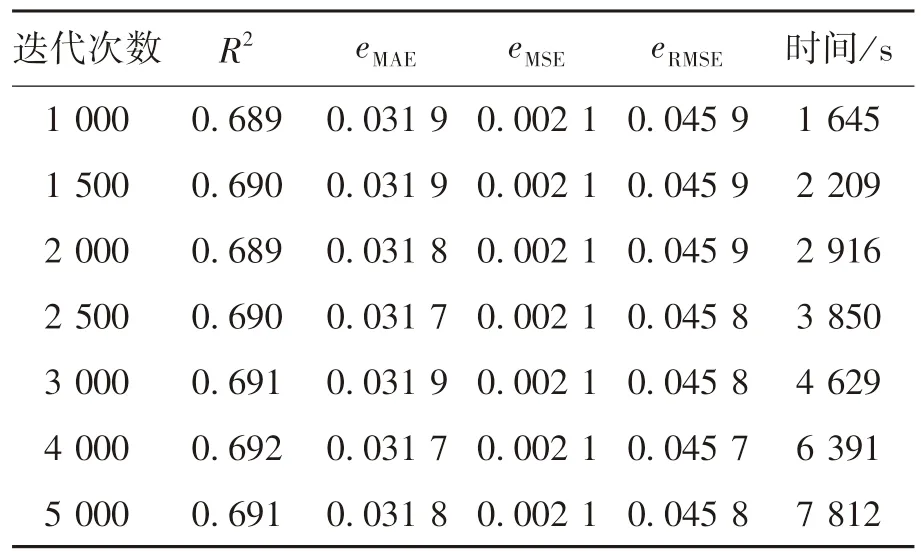
表7 RS 算法进一步优化结果均值Table 7 Mean value of further optimization results obtained by RS
3 模型验证
对比RS 算法、 GS 算法和BOA 算法对AdaBoost 模型超参数的优化效果和优化时间的影响,确定了基于GS 算法和AdaBoost 模型的LF 精炼过程脱硫率预测模型,其R2最大值为0.696.为了测试模型的预测性能,采集的数据集被随机地分为训练集和测试集,其比例为8 ∶2.从图7 中可以发现,RS 算法优化的AdaBoost 模型可达到脱硫率误差在±0.07,±0.06 和±0.05 范围内,准确率分别为95.3%,93.0%和86.0%,其中预测值和实际值的皮尔逊相关系数为0.84.这说明本文中提供的模型能够准确、稳定和快速地预测LF 精炼过程脱硫率.
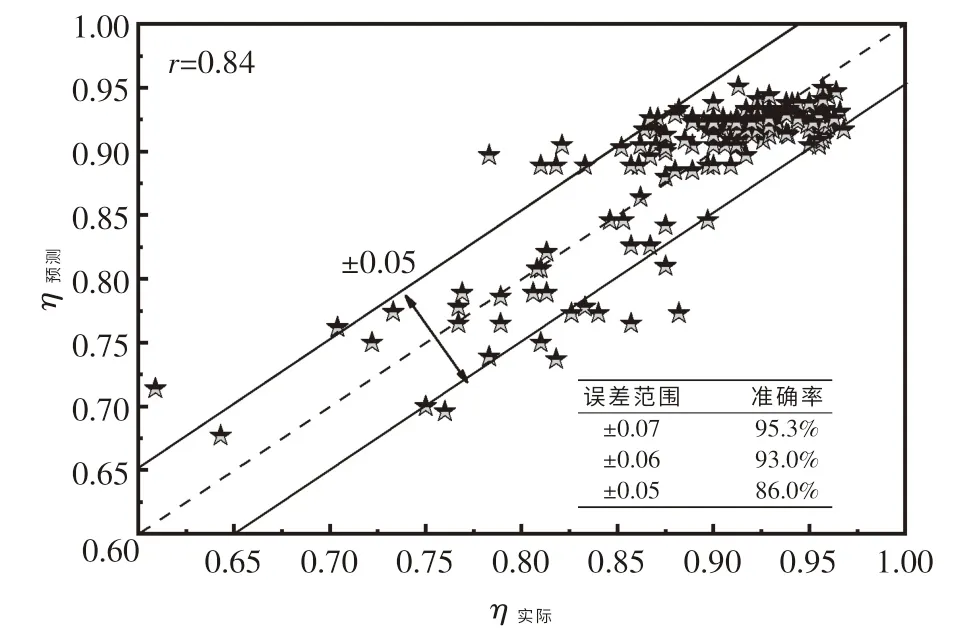
图7 脱硫率预测值与实际值对比Fig.7 Comparison between predicted value and actual value of desulfurization rate
4 结 论
(1)AdaBoost 模型比单一模型具有更好的拟合和泛化能力,能够更好地拟合LF 精炼过程中的实际生产数据.同时,AdaBoost 模型的内部超参数需要进行相互协调才能实现较好的预测效果.
(2)综合对比网格搜索算法、随机搜索算法和贝叶斯优化算法对AdaBoost 模型超参数的优化效果和优化时间的影响后可以发现,这3 种算法均能够有效地提升AdaBoost 模型的预测性能,而RS 算法更适合AdaBoost 模型的超参数优化.
(3)采用测试集对RS 算法优化AdaBoost 模型的回归能力进行验证,发现脱硫率误差在±0.07,±0.06 和±0.05 时,准确率分别达到95.3%,93.0%和86.0%,且预测值和实际值的皮尔逊相关系数达到0.84.因此,本模型具有较好的预测性能,可为LF 精炼过程提供有效的生产指导.

