图神经网络驱动的流域洪水预报技术
马森标
(福建中锐网络股份有限公司研发中心,福建 福州,350108)
0 引言
流域洪水预报是防汛抢险和防洪系统调度运用的决策依据,传统的洪水预报采用的机理模型[1]属于半经验半物理过程的预报模型,有一定的物理基础,但模型参数的率定十分复杂和困难[2],基于数据驱动的模型可根据海量的历史水文数据挖掘其潜在变化规律,具有比较高的性能和价值。
由于数据驱动模型的优点,目前国内已有很多专家学者将数据驱动的人工智能模型引入到洪水预报中。刘冬英等[3]提出了改进的BP 网络模型在洪水预报中的应用,取得较高精度的预报结果;金保明等[4]利用RBF 神经网络预报山区流域洪水的方法,取得了不错的预报精度效果;在闽江十里庵流量预报中应用BP 神经网络,预报精度符合要求[5];李晓丽等[6]提出了不确定支持向量机在洪水预报模型中的应用,获得了较高的洪水预报精度;马森标等[7]利用长短时记忆神经网络(LSTM)附加Attention 机制进行水库水位预报,取得了较好的性能。虽然以上算法在一定程度上提高了洪水的预报精确度,但是对于输入的数据特征,尤其是关键性的降雨、水位数据特征挖掘明显不足,关注了时序特征,却忽略了其本身具有的空间分布特征。同时,降雨量对水位的影响受到流域的地形、土壤、植被等自然因素的作用,表现出了显著的滞后性、持续性等特点。同样,受地理位置和流域地形的作用,泄洪量对水位的影响,及上游水位对下游水位的影响同样存在滞后性、持续性等特点。
图卷积神经网络(GCN)[8]是一种在图结构数据上运行的基于深度学习的扩展方法,可以挖掘符合非欧几里得空间域的流域数据结构,它能够从底层数据中提取出网络节点复杂的关联性[9]。
基于上述出发点,本研究提出了一个图指导的时空关联预报模型(GSCPM,graph-guided spatiotemporal correlation prediction model),用以预报流域水位。具体而言,该模型首先通过多个长短期记忆网络(LSTM)编码每个监测点历史属性的时间关联特征,随后利用挖掘监测点间的地理空间依赖,最后通过一个全连接神经网络进行回归预报,可解决流域洪水预报中的时空关系建模和滞后影响问题。
1 模型概述
在本节中,我们将详细介绍所提出的模型的实现细节,该模型的概述如图1 所示。
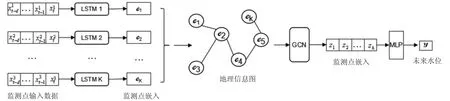
图1 GSCPM 模型
1.1 问题定义
流域水位预报问题的本质为多变量时间序列预报问题。设流域中有K 个监测点,第i 个监测点的可观测数据被定义为,其中t 为当前时间,d为过去时间天数,x∈Rn为该观测点包含的n 个变量,包括水位、降雨量和水库泄洪量。给定所有监测点的可观测数据,我们的目标是预报未来1 天的监测点水位
1.2 时间依赖编码
在获取K 个监测点的历史数据后,我们先通过LSTM 编码其时间依赖关系。由于每个输入点的特征维度可能不尽相同,并且只使用一个LSTM 可能无法区分不同监测点数据的特异性,我们为每个监测点设置了一个LSTM 网络,从而得到包含时间依赖的监测点嵌入:
其中,每个LSTM 的具体执行过程如下:
式中:Wf、Wi、WO、WC为可训练权重矩阵;bf、bi、bO、bC为可训练偏置矩阵;σ(·)和tanh(·)为非线性激活函数;ht-1为前一时刻的LSTM 单元的输出;[ ]∵ 为向量连接操作。
1.3 空间依赖编码
为编码获得时空融合特征,我们在时间依赖编码后,使用GCN 对所得嵌入进行基于地理空间关系的特征聚合。
一个地理信息图可由G=(V,E,C)描述。其中,V 表示图的节点集合,其中节点vi∈V 表示第i 个监测点;E表示边的集合,其中边eij∈E 表示节点vi和vj中存在关系;C 为节点的特征集合,其中ci∈C 为第i 个节点的属性值,我们将其设置为第i 个监测点的嵌入表示,即ci=ei。为使地理信息图能表示实际监测点间的地理关系,我们提出了一个简单有效的地理信息图构造方法。具体而言,遍历每个监测点,将其和流域河道中相邻的监测点都进行连接,如果该条边已经存在,则遍历下一个监测点。图2 展示了构图的一个示例。
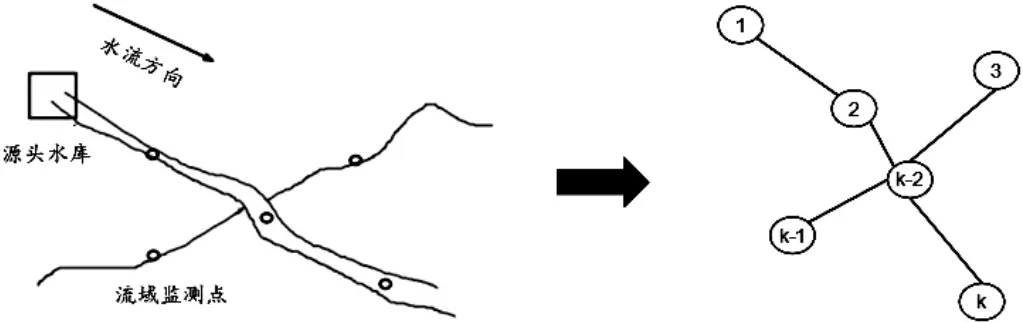
图2 拓扑结构图生成示例
经过上述构图操作,流域监测点的地理信息被融入图的拓扑结构之中。随后,使用一个GCN 聚合节点属性,从而将图的拓扑信息融入节点嵌入中。一个图卷积层的执行过程如下:
式中:D和A分别为图G 的度矩阵和邻接矩阵;W和b 分别是可训练的权重和偏置矩阵;l 和L 分别是GCN 执行的当前层数和最大层数。Zl为第l 层输出节点嵌入矩阵,同时作为下一层的输入。第一层GCN 的输入Z0为节点特征集C 中每个元素拼接而成的矩阵,GCN 的最终输出ZL被按行拆分K 个向量,代表每个监测点包含时空信息的嵌入表达。
1.4 回归预测
为进行最终的水位预报,K 个监测点的嵌入向量被按列拼接为新的向量Z。随后,采用一个全连接网络进行回归预测:
式中:WM和bM为可训练的权重和偏置矩阵;y 为最终预报的水位值集合,包含未来1 天的K 个监测点的水位值。最后,采用均方误差作为损失函数,用以反向传播训练:
式中:Y 为实际的水位值集合。
2 溪源流域水位预报研究
2.1 数据基本情况
本文选取福州溪源流域为研究对象,该流域共包含溪源水库及下游的侯官和融侨3 个监测点,其中溪源水库监测站点有泄洪量、降雨量数据,侯官和融侨站点有水位数据。通过章节1.3 所提出的构图方法,对3 个监测点进行构图,所得流域的时空示意图[9]如图3 所示。

图3 局部流域时空示意图
2.2 特征工程
通过机理和数学方法创造的特征,可以考虑到降雨量、泄洪量对水位的影响及上游水位对下游水位的影响都受到流域的地形、土壤、植被诸多自然因素的作用,构造的特征将融合滞后性、持续性特点,根据这些特征训练的模型具有更好的性能,这也是数据驱动模型优于机理模型的重要原因之一。
2.2.1 滞后特征构造
目前,在机器学习领域,降雨量、泄洪量和上游水位对流域水位的滞后效应,很难通过计算得到,通过构造相应的滞后特征,来模拟这些滞后影响,简化计算方法,提高建模效率。
一阶和二阶滞后特征的构造过程如图4 所示。假设原序列为{xt-d…,xt-1,xt},其m 阶段滞后则为其向左平移m 个时间点的序列,表示为{xt-d-m…,xt-1-m,xt-m}。在此基础上,设Rt(i)为t 时刻滞后(i-1)个时间单位的降雨量序列;Ft(i)为t 时刻滞后(i-1)个时间单位的泄洪量序列;Wut(i)为t 时刻滞后(i-1)个时间单位的流域上游水位序列;Wdt(i)为t 时刻滞后(i-1)个时间单位的流域下游水位序列,其中i≥2。

图4 滞后因素构造过程示例
2.2.2 降雨量滞后特征与水位特征的相关性分析
流域监测点在某一时刻的水位跟之前的降雨量密切相关,相关程度可以通过相关性的强弱来间接表示(见图5 图6)。

图5 雨量曲线图
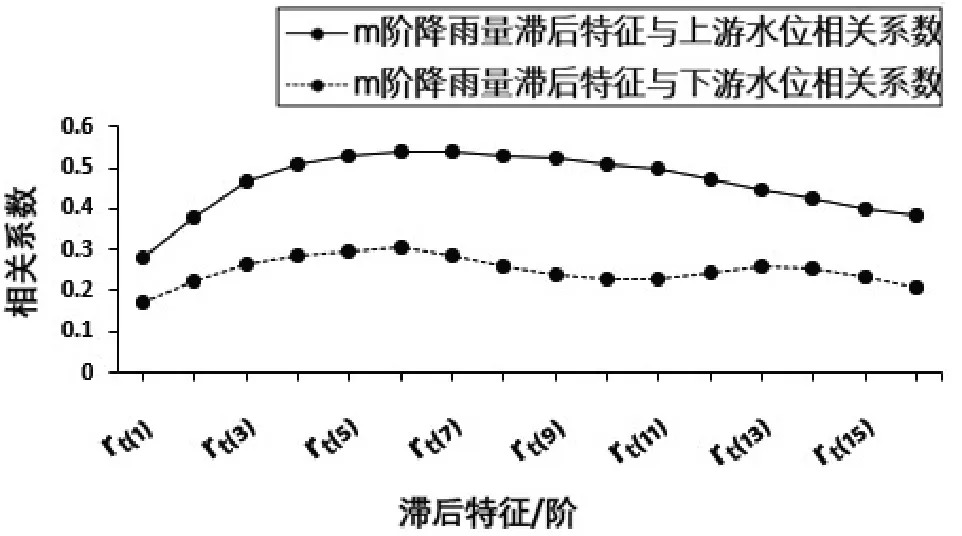
图6 m 阶降雨量滞后特征与上、下游水位相关系数曲线图
从表1 的相关系数可以看出,降雨量对水位的影响具有滞后效应,降雨量对水位的影响是逐渐加强的,随后逐渐减退,与蓄满产流的自然规律具有一致性。

表1 m 阶降雨量滞后特征与上、下游水位相关系数表
2.2.3 泄洪量滞后特征与水位特征的相关性分析
泄洪量对水位的影响巨大,在大坝某一时刻段的泄洪量,将持续影响流域监测点的水位,这个影响可以通过泄洪量和水位的相关性进行衡量,影响程度可以通过相关性的强弱来间接表示(见图7 图8)。
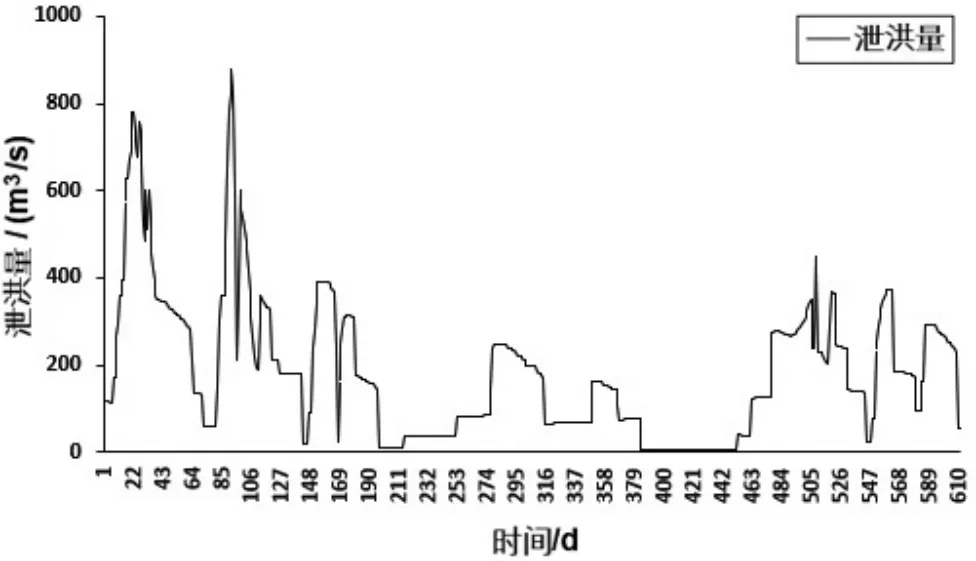
图7 泄洪量曲线图

图8 m 阶泄洪量滞后特征与上、下游水位相关系数曲线图
从表2 的相关系数可以看出,泄洪量对上、下游水位的影响具有持续性,泄洪量对上、下游水位的持续影响是渐渐变弱的,但都具有强相关性,符合水库泄洪河道水位陡涨的自然客观规律。

表2 m 阶泄洪量滞后特征与上、下游水位相关系数表
2.2.4 上游水位滞后特征与下游水位的相关性分析
在某一时刻流域下游监测点的水位跟该时刻前的上游水位密切相关,相关程度可以通过相关性的强弱来间接表示(见图9 图10)。

图9 上、下游水位曲线图

图10 m 阶上游水位滞后特征与下游水位相关系数曲线图
从表3 的相关系数可以看出,下游水位跟上游水位具有较强的相关性,随着时间的推移,相关性逐渐衰减,符合某一时刻的洪水波在传播过程中发生衰减演进的客观规律。

表3 m 阶上游水位滞后特征与下游水位相关系数表
2.3 数据集构建及数据预处理
基于章节2.2 中所展示的结论,我们添加相关度最高的滞后特征作为模型的输入。添加特征后,在溪源水库监测点包含泄洪量、泄洪量的1 阶滞后特征、降雨量和降雨量的6 阶滞后特征,共四个特征值;在上游流域监测点,共包含流域水位和流域水位的1 阶滞后特征两个特征值;在下游流域监测点,包含流域水位一个特征值。
由于水库水文数据包含水位、泄洪量、降雨量等数据,数值差异大,需要进行量纲的统一,以此提高模型的收敛速度和计算精度,因此,本文对序列的每一个特征值进行最大最小值归一化处理,即:
式中:x 为预处理序列的取值;xmin为序列的最小值;xmax为序列的最大值。
2.4 评价指标
本研究所采用的评价指标包括平均绝对误差(MAE,Mean Absolute Error)、均方误差(MSE,Mean Square Error)、平均绝对百分比误差(MAPE,Mean Absolute Percentage Error)三种,其定义如下所示:
2.5 实现细节
本研究的所有实验均用Pytorch(V1.7.0)[10]进行实现。为找到最优参数,我们使用网格搜索进行寻优。具体而言,学习率在{0.01,0.005,0.0025}区间进行搜索;正则化系数在{1e-5,1e-7,1e-9}区间搜索;历史时间长度在{2,4,16}中搜索;嵌入维度和LSTM 单元数在{8,16,32,64,128}区间搜索。此外,每次训练执行300 个epoch,并使用Adam[11]优化器优化模型参数。
2.6 实验结果
2.6.1 对比分析
为验证所提出的GSCPM 的有效性,我们将其与RNN、LSTM 和GRU 网络进行对比,表4 展示了这4 种方法的对比结果。可以看出,GSCPM 在三个指标上均明显优于其他三个方法。在所有方法中,RNN 表现得最差,LSTM 在解决RNN 梯度爆炸问题后得到了性能提升是明显的,GRU 在简化LSTM 后也带来一定的性能提升。然而,这些方法都无法考虑不同监测点间的空间相关性,因而限制了性能。将GSCPM 与LSTM 对比,LSTM 在添加GCN 后带来的性能提升是明显的,说明了时空关联预报对流域水位预报的重要性。

表4 GSCPM 及其对比方法的实验结果
2.6.2 消融分析
为验证空间依赖性和所构建的滞后特征的有效性,本研究设置了4 个子方法来与进行对比:
1)GSCPM(-rain):将降雨量滞后特征删除后的GSCPM。
2)GSCPM(-flood):将泄洪量滞后特征删除后的GSCPM。
3)GSCPM(-up):将上游水位滞后特征删除后的GSCPM。
4)GSCPM(-all):删除所有滞后特征后的GSCPM。
表5 展示了所有子方法的实验结果。从表中可看出,GSCPM 展示了最佳的性能和添加滞后特征的有效性。将GSCPM(-rain)、GSCPM(-flood)、GSCPM(-up)和GSCPM(-all)进行对比,它们三者都得到了不同程度的性能提升,说明所提议的三种滞后特征都能单独提升模型性能。此外,将GSCPM 与GSCPM(-rain)、GSCPM(-flood)、GSCPM(-up)进行对比,GSCPM 仍然具有性能提升,说明滞后特征的组合使用会带来更大的性能增益。
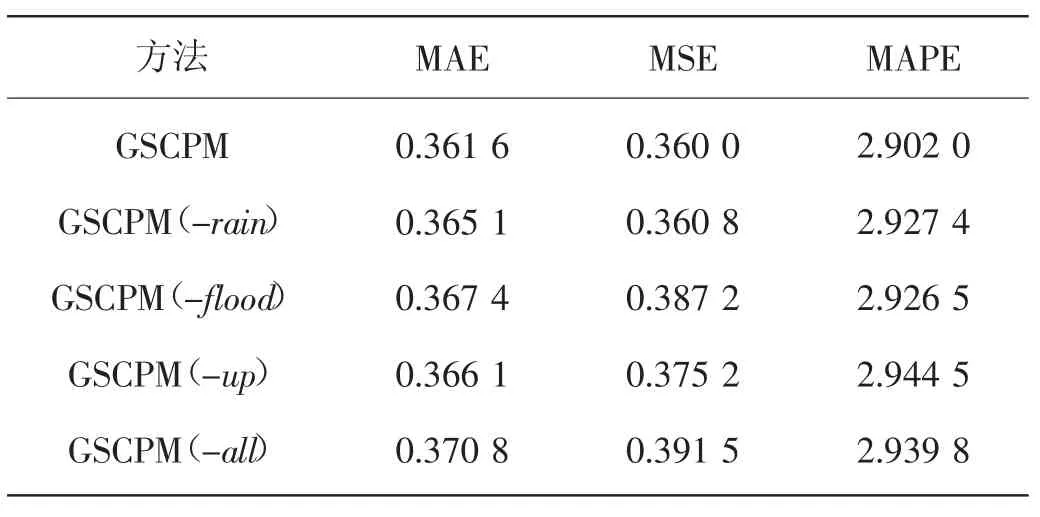
表5 GSCPM 及其子方法的实验结果
2.6.3 可视化分析
为进一步理解所提出的GSCPM 模型,我们将该模型及对比模型在测试集上的预报结果进行了可视化,其呈现如图11~图18 所示。可以看出,该模型在向前一步预报的情况下,基本拟合出了未来的变化趋势,只在少数突变情况下造成较大误差。值得注意的是,下游水位的真实值波动剧烈,然而GSCPM 仍能捕捉到大部分波动,形成较为精准的预报。相比于其他三个方法的可视化结果,GSCPM 能更好地拟合真实水位曲线,也能更好地预报出突变情况,这也表明为什么我们的方法在众多评价指标上表现得最好。

图11 GSCPM 上游预报结果可视化
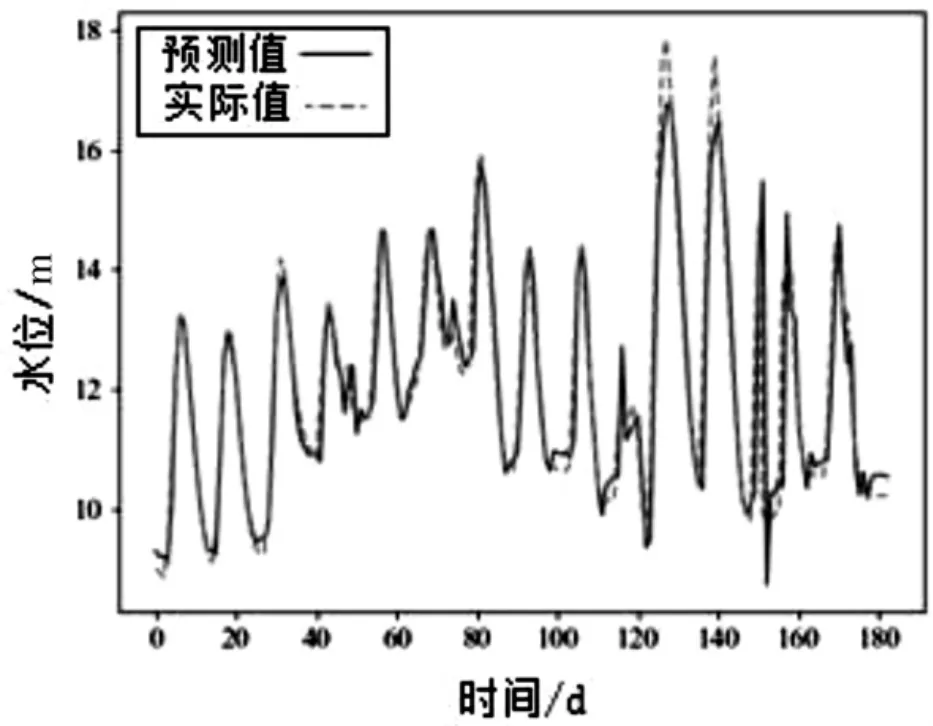
图12 GSCPM 下游预报结果可视化

图13 RNN 上游预报结果可视化

图14 RNN 下游预报结果可视化
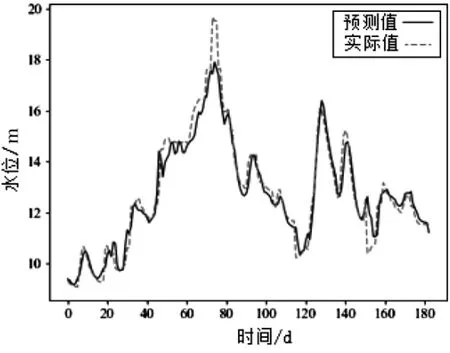
图15 LSTM 上游预报结果可视化
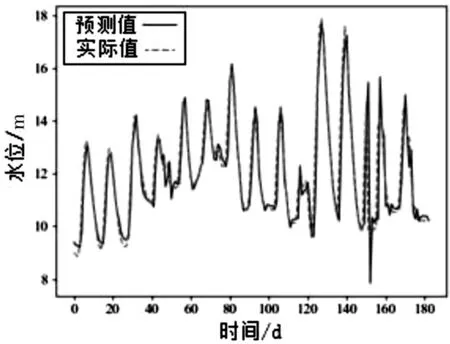
图16 LSTM 下游预报结果可视化

图17 GRU 上游预报结果可视化
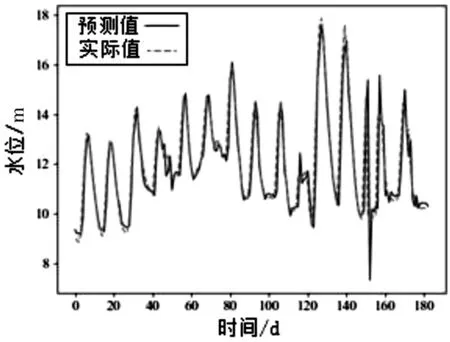
图18 GRU 下游预报结果可视化
3 结论
本研究提出了一种图指导的时空关联预报网络模型,用以针对性地解决流域洪水预报中的时空关系建模问题和滞后影响问题。实践证明,该模型可以有效降低对流域数据维度的要求,并挖掘流域洪水跟降雨量、泄洪量、上游水位和下游水位之间复杂的时空关联性。本文提供的是流域2 个节点的洪水预报模型,接下来将研究通过图神经网络节点的扩展,通过一个图神经网络模型,对整个流域的洪水进行预报的可行性问题,以促进流域洪水预报的广泛实践。

