一类单圈图的最小能量
王智玉, 高玉斌
(中北大学 数学学院, 太原 030051)
1 引言与主要结果

设G是一个n阶简单连通图, 其顶点集为V(G)={v1,v2,…,vn}, 边集为E(G),dG(vi)表示图G中顶点vi的度,NG(vi)表示顶点vi的邻集, 其中i=1,2,…,n.若dG(vi)=1, 则vi称为G的悬挂点.边数等于顶点数的连通图称为单圈图.用G(n,l)表示围长是l且顶点数是n的连通单圈图.Cg∪St是通过连接圈Cg上的一顶点与星图St的某一悬挂点或中心点组成的一类单圈图.




(1)



(2)


2 预备知识



引理1[14]设G∈G(n,l), 则对所有的k≥0均有(-1)ka2k≥0.若l=2r+1且r是奇数(或偶数), 则对所有的k≥0均有(-1)ka2k+1≥0(或≤0).
由式(2)可得
(3)
为方便, 本文设bi(G)=|ai(G)|, 则εR(G)是一个关于参数bi(G)的单调递增函数, 其中i=1,2,…,n, 即以下结论成立.
引理2[14]设G1和G2是两个单圈图, 如果对所有的i≥0均有bi(G1)≥bi(G2), 则εR(G1)≥εR(G2).
3 给定单圈图的图变换
3.1 变换Ⅰ


图1 变换ⅠFig.1 Operation Ⅰ

1) 0 当i=2k≥4时, 有 即 2)g≤i≤g+1. ① 围长g为偶数.当i=g=2k时, 有 即 若g≡2(mod 4), 则式(4)中的符号“±”为正; 若g≡0(mod 4), 则式(4)中的符号“±”为负. ② 围长g为奇数.当i=g时, 有 即 图2 变换ⅡFig.2 Operation Ⅱ 即 即 若g-1≡2(mod 4), 则式(5)中符号“±”为正; 若g-1≡0(mod 4), 则式(5)中符号“±”为负. 设图G3∈Cg∪St是通过连接圈Cg上的一顶点与星图St的中心点而生成的单圈图Cg∪St, 其中Cg=u1u2…ugu1, 圈长g≥6且g为偶数.设 图3 变换ⅢFig.3 Operation Ⅲ 当i=2k=2时, 有 当i=2k=4时, 有 即 图4 变换ⅣFig.4 Operation Ⅳ 证明: 易得 其中n≥4.因此 由式(2)知, 故



3.2 变换Ⅱ







3.3 变换Ⅲ
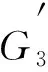

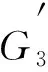


3.4 变换Ⅳ




4 定理1的证明



