基于参数辨识的DTP-PMSM无传感器控制*

王 帅,张会林,张建平

(上海理工大学机械工程学院,上海 200093)

0 引言

多相电机因具有高功率密度、高可靠性、转矩脉动小等优点,在各个领域得到了广泛的应用[1]。其中,双三相永磁同步电机(DTP-PMSM)因可以直接使用市面上的三相逆变器便可以对其控制,因而得到了广泛的应用[2]。

在电机运行过程中,因外界和电机本身的原因,电气参数容易发生变化,且传感器精度也会受到影响,为了保证系统的控制性能[3]。因此把在线参数辨识和无传感器控制结合起来具有重大意义。

目前,常用的参数辨识方法包括最小二乘法[4]、卡尔曼滤波器[5]、模型参考自适应方法(MRAS)。刘金海等[6]针对永磁同步电机方程欠秩问题,在q轴电压方程和递推最小二乘法相结合的方法,辨识出电气参数。李婕等[7]采用改进标准粒子群算法优化最小二乘法,提高系统的辨识速度和精度。张晓虎等[8]利用扩展卡尔曼滤波算法优化观测器中的增益矩阵,并且构造一种自适应率函数动态调整传统EKF中固定的噪声协方差矩阵,提高观测器的抗扰动性能。但这些算法生成的结果具有不确定性,这样就会对系统的控制性能产生影响。MRAS因具有结构简单、响应速度快、算法计算量小等优点得到了广泛的应用,但是其存在欠秩问题。李垣江等[9]提出一种改进模型参考自适应系统的分步在线辨识方法,先辨识定子电阻和转子磁链,再辨识电感。姚绪梁等[10]提出了一种级联MRAS参数辨识方法来辨识系统电气参数。

在无传感器控制中,通常使用PLL来获取电机的转速和位置信息。虽然传统PLL跟踪效果很好,但是其在电机加减速时,就会存在稳态误差的问题[11]。李海剑等[12]使用三阶3类锁相环,通过合理的配置锁相环系统零极点,可快速有效地消除电机运行中的动态跟踪误差,但在遇到负载扰动时,需要更高阶的PLL,这样会使计算量迅速增加。王金柯等[13]使用滑模锁相环,但滑模存在的抖振问题会对系统的精度产生较大影响,特别是遇到高频扰动时,其影响会更大。王明辉等[14]把ESO应用到PLL中,构建了一种高阶PLL,引入加加速度这个变量,其结构较为简单,响应速度快速。

本文把MRAS和磁链观测器结合起来,并使用BP神经网络来优化自适应律的增益,不仅可以在电气参数变化时,及时辨识出新的电气参数并更新到控制系统中,还能对自适应律的参数进行在线调节,提高系统的辨识精度。同时,提出了一种基于线性扩张状态观测器(LESO)和滑模控制(SMC)相结合的改进锁相环(LESO-SMC-PLL),通过Lyapunov函数证明所提PLL在电机加减速时,可以消除系统的稳态误差。最后,通过仿真验证本文所提方法的优越性和有效性。

1 静止坐标系下MRAS设计

在DTP-PMSM中,α-β静止坐标系下的电流方程为:

(1)

式中:iα、iβ、uα、uβ为α-β轴定子电流和电压,ψα、ψβ为α-β轴磁链,ωe为电角速度,R、L为定子电阻和定子电感。

由式(1)构造α-β轴定子电流估计方程为:

(2)

将式(1)和式(2)做差可得,电流误差方程为:

(3)

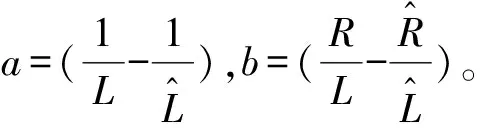
为了便于分析,式(3)可写为如下形式:

(4)

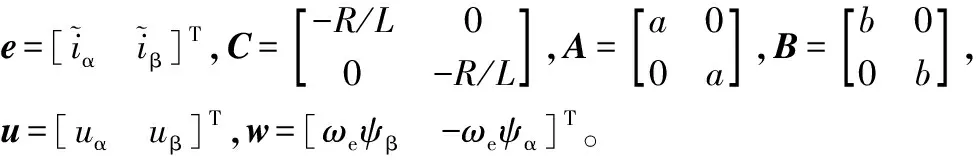
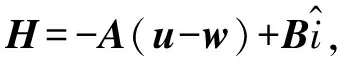
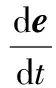
(5)

依据Popov超稳定性理论可知,若使该系统稳定,必须满足:

(1)传递函数G(s)=(sI-C)-1为严格正定矩阵;

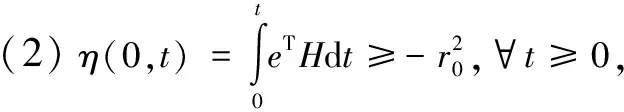
对于条件1:

(6)

可以看出式(6)的顺序主子式均大于0,故该传递函数严格正定。

对于条件2:

(7)

将其拆解为:

(8)

在此,对式(8)中的η2(0,t)成立进行证明。把B带入η2(0,t)可得:

(9)

以PI形式设置相应的自适应律为:

(10)

将式(10)带入式(9)并将其拆为两部分可得:

(11)

假设:

f′(t)=eT

(12)

(13)

根据不等式:

(14)

由此可得:

η22(0,t)≥-f2(0)

(15)

假设:

(16)

则:

(17)

由此可得基于PI设计的自适应律满足Popov稳定性要求,此时系统渐进稳定。

同理可得电感的自适应律为:

(18)

当参数R和L被辨识后,作为已知量输入到磁链观测器中,如下式:

(19)

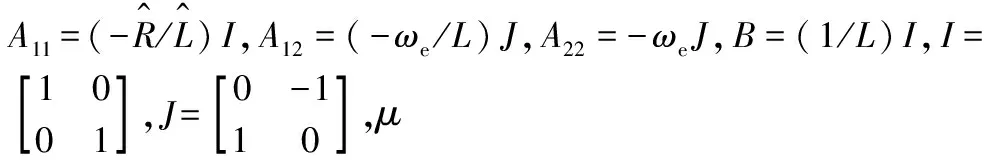
H=-LI+l1LJ

(20)

式中:l1为实数。

2 PI增益优化设计

根据以上的分析可知,电感和电阻的辨识精度取决于自适应律中的比例积分增益。通常情况下,比例积分增益是固定不变的。但是系统在运行时,会受到各种因素的影响,造成电气参数的变化,这时固定积分增益可能会产生较大的辨识误差。因此,在线增益调节对系统的控制性能十分重要。

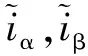
采用前一次输入误差和后一次输入误差的二次方为性能指标,此时性能指标函数为:

J=min[r(k)-r(k+1)]2

(21)

BP神经网络算法流程图如图1所示。

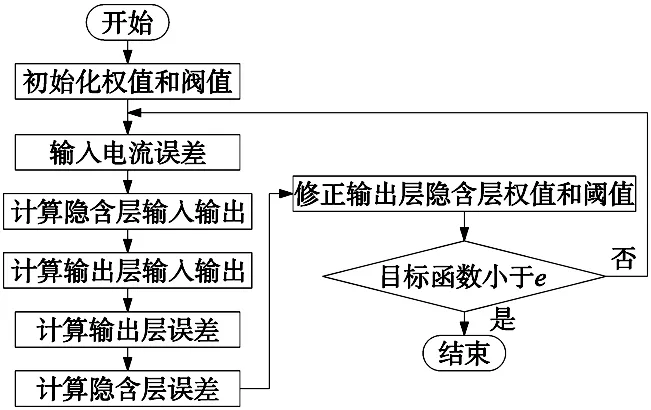
图1 BP神经网络优化流程图

按照梯度下降法修正网络加权系数,并添加使搜索快速收敛至全局极小的惯性项,此时输出层的加权系数为:

Δw(k+1)=ηδioi(k)+αΔw(k)

(22)

(23)

式中:g′(x)=g(x)(1-g(x)),g(x)为输出层激活函数。

同理可得隐含层的加权系数:

Δw(k+1)=ηδjoi(k)+αΔw(k)

(24)

δj=f′(netlk)∑δjwk

(25)

式中:f′(x)=(1-f(x)2)/2,f(x)为隐含层激活函数。

3 LESO-ESO-PLL的构建

为了克服传统PLL在电机加减速时,会存在稳态误差的问题,提出一种线性扩张观测器和滑模控制相结合的改进PLL。

基于LESO-SMC的PLL控制系统的模型如图2所示。

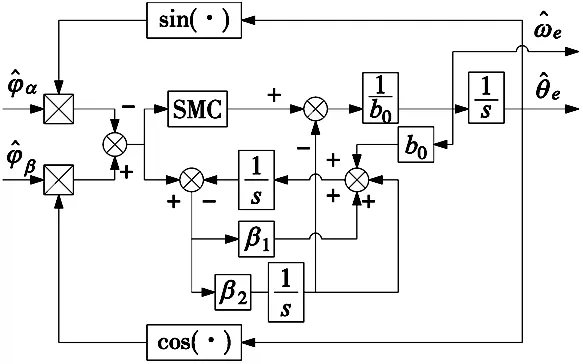
图2 LESO-SMC-PLL模型

3.1 LESO的构建

当考虑系统扰动时,θe与ωe之间的关系构造为:

(26)

式中:f表示系统的总扰动。

式(26)可以变化为以下形式:

(27)

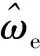
(28)

根据式(28),LESO的方程可以表述如下:

(29)

式中:z1是x1的估计值,z2是总扰动x2的估计值,β1和β2是LESO的增益。

用式(28)减去式(29),其观测误差为:

(30)

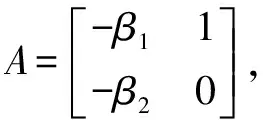
λ(s)=(sI-A)=s2+β1s+β2

(31)

由Hurwitz稳定性判据可得:当系统极点在左半平面则系统稳定。把系统极点配置在-ω0可得:

s2+β1s+β2=(s+ω0)2

(32)

3.2 LESO-SMC的构建

选择滑模面:

s=cx1

(33)

式中:c为正实数。

对上式求导:

(34)

当系统达到稳定状态时,s趋近于0,s的积分趋近于0。为此,设计出具有积分形式增益的滑模控制器,使当s趋近于0时,切换项的增益趋近于0,从而达到消除抖振的目的,故选择如下趋近律:

(35)

(36)

式中:Kp>0,Kf<0。

联立式(28)、式(34)、式(35)可得:

(37)

为了证明系统的稳定性,选取 Lyapunov 函数为:

(38)

对上式求导可得:

(39)

4 仿真分析

为了验证本文所提辨识模型的有效性,在MATLAB/Simulink平台上进行仿真实验,根据VSD变换的特点,本文采用id=0,ix=0,iy=0的矢量控制方法。电机参数如表1所示。本次仿真在负载20 N·m的条件下进行,系统整体仿真框图如图3所示。

表1 DTP-PMSM参数表

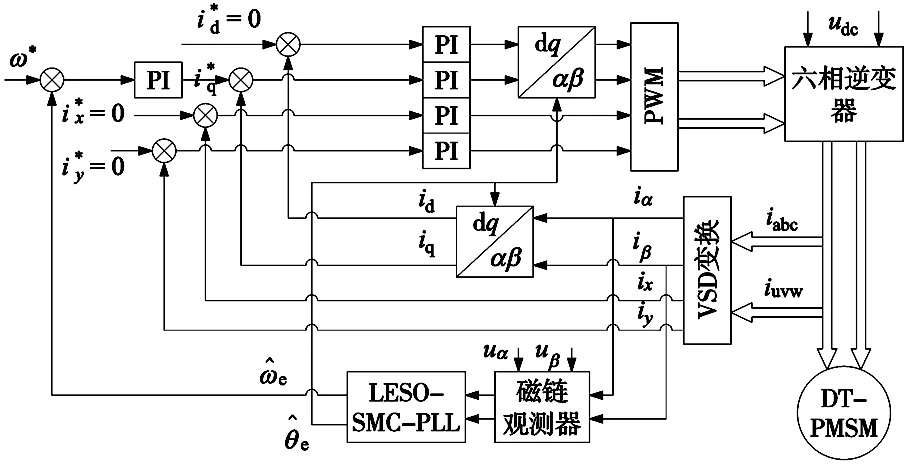
图3 系统整体仿真框图

工况1:变阻运行。给定转速500 r/min,负载启动,初始电阻为1.4 Ω,在0.1 s电阻突变为3 Ω。仿真结果如图4～图6所示。

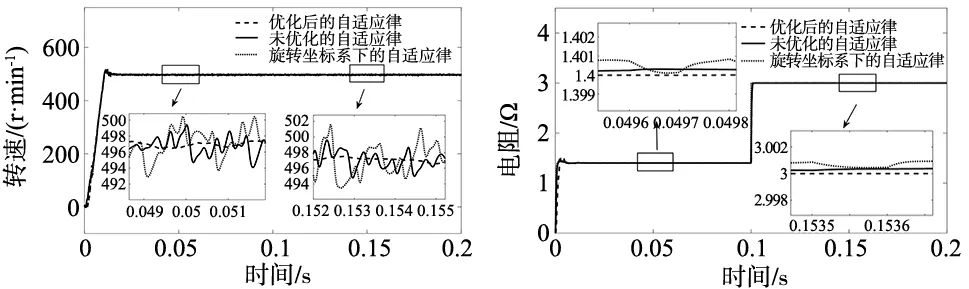
图4 转速对比 图5 定子电阻辨识对比

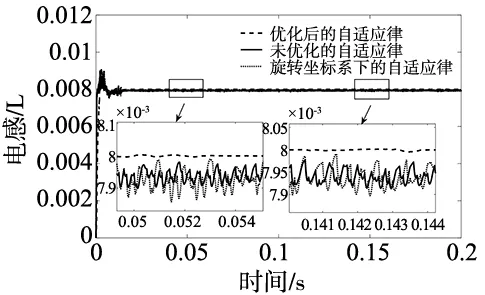
图6 定子电感辨识对比

由上图可以看出,采用旋转坐标系下设计的自适应律时,电机中的谐波电流得不到较好的抑制,导致电感和电阻的辨识出现较大的波动,进一步影响系统的控制性能,导致电机转速波动较大,当在静止坐标系下设计自适应律时,不论是电感辨识、电阻辨识精度还是电机转速波动均明显改善,但是其波动仍然较大。当加入BP神经网络优化后,可以看出系统辨识结果更加精确,且波动更小,提高了系统的控制性能,可以看出自适应律增益对系统的辨识精度会有很大的影响。

工况2:变感运行。给定转速500 r/min,负载启动,初始电感为0.008 H,在0.1 s时变为0.01 H。仿真结果如图7～图9所示。

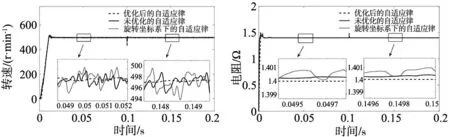
图7 转速对比 图8 定子电阻辨识对比

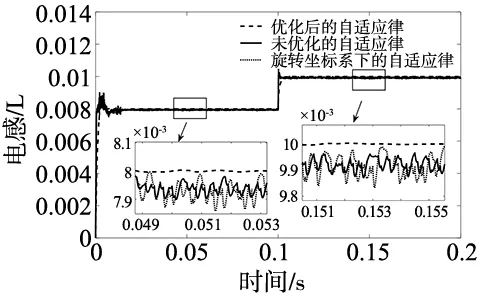
图9 定子电感辨识对比

由上图可以看出,加入BP神经网络优化后,电感、电阻的辨识效果同样更好,且转速波动同样更小。加入BP神经网络优化后,在电感突变时的响应速度略慢,但是在系统达到稳定状态时,可以明显看出其辨识值更加接近真实值。

为了验证本文所提LESO-SMC-PLL的有效性,图10和图11分别使用LESO-SMC-PLL和ESO-PLL对系统进行控制,在0.1 s分别进行加载运行和变速运行。

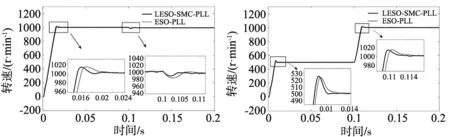
图10 加载运行 图11 变速运行

由上图可以看出,LESO-SMC-PLL在变速运行时,更快达到稳定状态,在受到负载扰动时,表现出更强的鲁棒性。

5 结论

针对DTP-PMSM在受到外界和内部影响时,会造成电气参数变化和传感器精度不高的问题,提出一种MARS和磁链观测器相结合的无传感器控制方案。通常MRAS是基于旋转坐标系设计的,为了减小谐波电流的影响,本文将其推广到静止坐标系中,利用Popov超稳理论来设计自适应律,为了在电气参数变化时更好的辨识其真实值,使用BP神经网络对其进行优化。由于电机在受到扰动时,转速会发生变化,传统PLL在转速出现变化时,会存在较大的稳态误差,故提出使用LESO-SMC-PLL来代替传统的PLL,通过Lyapunove函数证明其不论何种情况下,都能达到稳定状态。仿真结果表明,所提方案可以实现对定子电感和电阻的准确估计,提升系统的控制性能。