土壤污染场地多无人车的路径规划与运输任务分配算法

金冰慧，孙阳，吴文君，翟梦荻，高强，司鹏搏

北京工业大学信息学部

随着我国城市化进程的加快和产业的调整升级，焦化厂等重污染企业逐渐搬离或关停[1-2]，污染场地的修复和治理工作刻不容缓。土壤修复技术成为日益关注的焦点[3]，用于土壤修复的智能化设备创新与研发也势在必行[4-5]。近年来，人工智能技术不断发展，其在环境监测与治理场景中的应用越来越广泛[6-7]。考虑到焦化场地的多环芳烃等典型污染物性质稳定难以降解，又对人体有极大的危害[8-9]，为了提高运输污染土壤的安全性和效率，采用智能化的无人设备进行污染土壤修复工作具有重要意义。随着科学技术的发展，智能无人车（unmanned ground vehicle，UGV）已经被应用在医疗、军事、交通、采矿、农业等领域以进行探测、搜索、救援和运输任务[10-11]，在危险环境中利用无人车进行工作已是大势所趋。

在多无人车协同进行土壤污染场地受污染土壤的运输工作中，为保证多无人车安全、高效、精准地运输污染土壤，需要根据土壤污染场地具体的地形地貌特点建立多无人车路径规划和任务分配模型。在路径规划方面，对于传统的路径规划算法[12-13]，如A*、人工势场等，面对场地规模和运输任务数量的增加时，这些算法的实时性和稳定性会变差。对于包括蚁群优化(ant colony optimization,ACO)[14]、粒子群优化(particle swarm optimization,PSO)[15]、遗传算法(genetic algorithm,GA)[16]在内的智能算法虽具有处理复杂路径规划问题的自学习和自我更新能力，但由于其算法计算复杂度较高，很容易陷入局部最优解。近年来，深度强化学习(DRL)算法已广泛应用于无人车的路径规划之中[17-18]，通过不断训练无人车与土壤污染环境的交互过程，持续优化网络参数并输出最优路径决策。在任务分配方面，传统的解决方法包括利用拍卖算法[19]、匈牙利算法[20]、遗传算法[21]等进行任务分配，但大多数研究往往专注于已知路径开销下任务分配问题的求解，并没有考虑路径规划对系统开销的影响。

本文以某一污染严重的焦化厂为研究环境，设计多无人车智能运输模型，集自动导航、路径规划与协同调度等技术于一体，对污染土壤运输过程实施精准控制和智能优化，提高修复效率。在土壤污染场地多无人车协同运输的工作场景下，考虑了土壤污染场地的复杂地形地貌特点和实际系统开销，设计了基于深度 双Q 网络 (double deep q-network,DDQN)和ACO 算法的多无人车路径规划和任务调度机制以提高污染土壤运输效率。首先，利用车联网技术构建多无人车系统以实现各无人车以及中央控制器间的有效通信，并建立运输场景下的多无人车路径规划和任务分配组合优化问题模型；再分别利用DDQN 和ACO 算法进行路径决策优化和任务执行序列优化。充分考虑特殊应用环境和车联网系统的特点，对复杂环境下无人车路径规划和协同优化问题进行研究，以期为今后在污染环境修复、灾后营救、矿区开采等特殊环境下的多无人车协同工作提供参考。

1 土壤污染场地多无人车协同调度与路径规划问题模型

1.1 运输任务场景

针对土壤污染场地中的多无人车污染土壤运输场景（图1）进行研究，该场景中主要包含崎岖起伏的土壤污染场地、处理中心、若干运输无人车、若干存储待运输的污染土壤堆的任务节点以及障碍物等。主要利用多无人车将所有待处理的污染土壤运输到处理中心统一进行处理，其中多个无人车统一由处理中心出发至各任务节点，装载并运输污染土壤，最终回到处理中心。为方便对多无人车的控制以及进行车辆之间的通信，基于车联网技术建立多无人车系统。首先，在网络中选取一个节点作为集中控制器，集中控制器不仅可以利用车联网的无线通信技术与多辆无人车进行通信，还可以用于集中收集和分析环境、任务以及无人车的数据信息，并利用这些信息训练和优化系统模型。土壤污染场地中的多无人车可以利用定位和感知技术收集其周围一定范围内的环境和任务信息，并通过无线通信技术将收集到的信息上传至集中控制器。集中控制器对接收到的各无人车的局部信息进行整合分析，利用这些数据训练模型。最后，集中控制器将路径规划和任务分配模型输出的各无人车最优动作决策以及执行任务序列分发给对应无人车执行，以减少系统开销，提升运输效率。

图1 多UGV 智能运输任务场景Fig.1 Multi-UGV intelligent transportation task scenario

由于雨水的侵蚀和地表水结构的变化，土壤污染场地的地面通常崎岖不平，大量废弃污染物长期覆盖在土地表面，产生的有毒酸碱性物质渗入土壤，导致土壤性状产生变化。因此，为了建立合理的环境模型，利用栅格法将环境划分为规则若干栅格，对每个栅格赋予信息表示其地形情况，建立基于地势的三维环境模型。多UGV 运输场景中的UGV 和任务具有不同的标识。将M个UGV 集合表示为M={1,2,···,M}，N个运输任务集合表示为T={T1,T2,···,TN}，假设各UGV 的装载量相同，所有运输任务量相同，每个UGV 的单次最大装载的任务数量为g，每个UGV 被分配执行的任务集合可表示为 Tm，UGVm被分配的运输任务的数量表示为nm。

规定UGV 每次动作由当前栅格中心移动至下一栅格的中心，且动作被限制在以90°分隔的前、后、左、右4 个方向。由于土壤污染场地环境地形表面并不平坦，考虑实际情况，当相邻2 个栅格间的地形坡度较大时，为了安全UGV 可能选择绕路。定义坡度为当前栅格与下一栅格的中点高度连线与水平方向的夹角，用 α表示。UGV 在环境中单步行驶的速度v与坡度有关，当UGV 从高度较高的栅格移动到较低的栅格或从高度较低的栅格移动到较高的栅格时，UGV 将以比在平坦地形中更低的速度行驶更长时间。

1.2 优化问题建模

对于任意任务Tj、Tk，（Tj,Tk∈T ），用 ξjk(Pjku)表示UGV 从任务Tj到Tk的 第u条路径所用的时间，对每个任务Tj都有 ξjj=0 。设σjkm:T×T×M →{0,1}为任务分配标识，它将起始和结束位置的索引Tj、Tk和m(U GVm∈M)之间的关系映射为一个二进制值，当且仅当指定 UGVm在任务Tj和Tk之间移动时，该值为1，否则为0。对于所有Tj和m，存在 σjjm=0，为了更好地描述约束，定义了一个映射χjm:T×M →{0,1}，将任务Tj与 UGVm映射为一个二进制值，当且仅当指定U GVm服 务于任务Tj时，该值为1，否则为0。

为提高污染土壤运输效率，缩短运行周期，土壤污染场地场景下多UGV 的路径规划和任务分配策略以最小化多UGV 的总时间开销为优化目标，且必须满足一些约束条件以保证路径规划和任务分配的有效性，优化目标可建模如下：

满足约束条件

其中：式(4)为每个任务由且仅由一个UGV 完成；式(5)和式(6)确保到达和离开相同的任务的是同一个UGV；式(7)为每个UGV 的总运输任务量不大于其最大装载量；式(8)为每个UGV 运输的任务不重复；式(9)为M个UGV 共同完成N个运输任务。上述问题是一个具有无穷解集的组合优化问题，无法通过简单穷举来解决，因此很难求解。

2 DDQN-ACO 路径规划和任务分配算法

针对上述土壤污染场地的多UGV 路径规划和任务分配的组合优化问题，笔者提出了一种DDQNACO 路径规划和任务分配算法来求解此问题。首先将原问题分解为路径规划和任务分配子问题分别进行求解。利用基于DDQN 的路径规划算法来获得各任务节点间的最优路径和实际路径开销，并基于此开销矩阵，使用ACO 算法解决多UGV 的任务分配问题。

2.1 基于DDQN 的路径规划算法

2.1.1 建立MDP 模型

土壤污染场地的多UGV 路径规划问题可以看作是UGV 和土壤污染环境间一个连续的交互过程，可以利用深度强化学习算法进行求解。马尔可夫决策过程(Markov decision process,MDP)通常可以用来描述深度强化学习问题。本文中UGV 可以获取污染环境地形、环境边界、障碍物位置等信息作为动作选择的依据，因此，可以将三维环境中的UGV 路径规划问题建模为MDP 模型。MDP 模型(S,A,R,γ) 包含状态空间 S，动作空间 A、奖励函数R和折扣因子 γ。状态空间 S由UGV 的全局环境信息 G、当前位置信息su和目标位置信息sg构成。UGV 在任意时刻的状态可表示为st=(G,su,sg)∈S。动作{空间 A表示UGV 的} 4 个移动方向，表示为A=前进,后退,左转,右转。γ 为折扣系数，γ ∈[0,1]，用于描述未来奖励函数的重要性。R为奖励函数，指UGV 在采取动作后获得的奖励。在路径规划训练过程中，奖励函数的设计非常重要。为了行车安全，UGV 应避开障碍物；为了提高系统的运输效率，应该结合地形因素，缩短UGV 到达目标的时间，以节省系统开销。因此，将奖励函数设置为：

式中：r1为当UGV 到达目标时获得的 奖励；-r2为UGV 遇到障碍物时的惩罚。

2.1.2 DDQN 算法

DDQN 是一种典型的深度强化学习算法，由评估网络和目标网络构成（图2）。DDQN 算法在训练过程中，通过将2 个神经网络输出的差值作为误差进行反向传播，优化每个神经元的权值，使误差最小化。

图2 神经网络训练过程Fig.2 Neural network training process

UGV 利用 ε-greedy策略来选择动作at=，通过执行动作at获得相应的奖励Rt并进入下一个状态st+1。将(st,at,Rt,st+1)存储在记忆库中，神经网络从记忆库中随机取部分样本进行训练。为了提高预测精度，目标网络Q值更新如下：

式中：Rt为t时刻的即时奖励；st+1为下一时刻的状态；θ为评估网络的参数；θ-为目标网络的参数。其损失函数为 Loss(θ)=E{[φt-Q(st,at;θ)]2}。经过一段时间的训练后，得到土壤污染场地中任意2 个任务Tj和Tk之 间的最优路径和路径开销，并生成开销矩阵 L：

2.2 基于ACO 的多UGV 任务分配模型

2.2.1 运输任务分配模型

在土壤污染场地多UGV 的运输任务分配模型中，所有UGV 从同一个处理中心出发，到各任务点运输污染土壤并返回处理中心（图3）。基于DDQN路径规划算法获得的开销矩阵 L，可将原组合优化问题转化为任务分配问题：

图3 任务分配模型Fig.3 Task assignment model

式（13）满足式(4)、式(7)～(9)的约束条件。这是一个典型的多旅行商问题（mTSP），可采用ACO 算法进行求解。

2.2.2 ACO 算法

ACO 算法是一种群体智能优化算法，由Colorni 等人于1991 年首次提出[22]。该算法通过模拟真实蚁群选择路径，寻找食物源和巢穴之间的最短路径。在觅食过程中，蚂蚁会沿着路径释放出一种可以被其他蚂蚁检测到的信息素。当越多的蚂蚁通过这条路线时，会积累更多的信息素。随着信息素浓度不断更新，信息素将吸引更多蚂蚁前往更短的路线[23]。利用ACO 算法解决多UGV 任务分配问题的步骤如下。

式中：ϖ为信息素因子；β为启发式因子；Tq为Tj的未访问任务集；τjk为路径(Tj,Tk)上 的信息素浓度；ηjk为启发式信息。持续根据式（14）选择 Tq中的下一个任务，直到 Tq为空。

此外，为了更好地探索全局最优解，使用2-opt方法来优化每个UGV 的局部任务序列 Tm[24]。重复上述步骤不断迭代并更新信息素[25]，最终输出当前的最优任务分配策略。

3 结果与分析

3.1 仿真设置

为验证所述DDQN-ACO 算法在土壤污染场地进行污染土壤运输任务的有效性，基于python 语言编程建立虚拟仿真环境进行试验和分析。模拟仿真土壤污染环境设置为150 m×150 m 的正方形区域，划分为30×30 个栅格，环境的高度区间以 λ=0.5 m为单位区间进行划分，并用不同颜色表示不同的高度间隔（图4）。在该仿真环境中设置1 个处理中心C，4 个UGV 和12 个待运输任务，设UGV 最大装载量可以运输3 个任务。DDQN 神经网络的参数如表1 所示。使用ACO 算法进行任务分配中涉及的主要参数如下：信息素的挥发率 ρ为0.03，信息素因子 ϖ为1，启发式因子 β为3，最大迭代次数为50，每次迭代随机生成的决策数量为200，2-opt 方法的迭代次数为20。

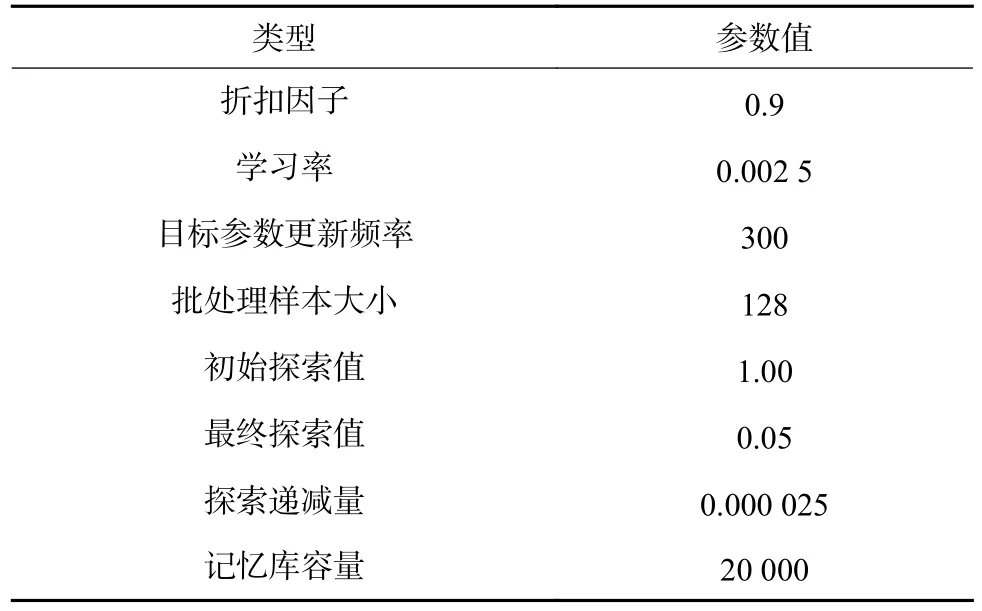
表1 神经网络的参数Table 1 Parameters of neural network

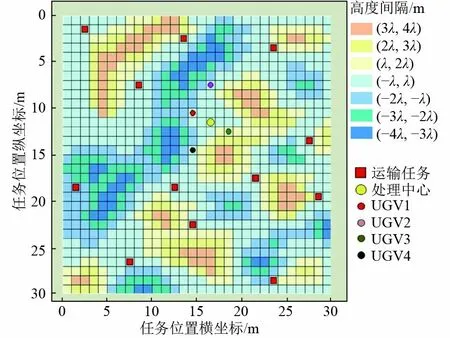
图4 仿真环境示意Fig.4 Simulation environment diagram

为验证本文提出的DDQN-ACO 算法的性能，提出以下比较方案：1）Manhattan-ACO，使用ACO 算法根据任意2 个任务之间的曼哈顿距离进行任务分配；2）DDQN-greedy，使用贪婪算法根据DDQN 训练得到的所有运输任务间的实际路径开销进行任务分配。

3.2 仿真结果

基于上述仿真环境及算法进行学习和训练，利用DDQN 算法训练UGV 在土壤污染场地中不断探索学习，最终得到UGV 在处理中心和各运输任务两两之间的路径开销并生成开销矩阵，再基于开销矩阵进行任务分配。表2 显示了基于不同算法得到的每个UGV 的具体任务分配策略和路径对应的时间开销。由表2 可见，基于DDQN-ACO 算法得到的总路径开销为347.50 s，基于Manhattan-ACO、DDQNgreedy 算法得到的路径开销分别为362.50、413.75 s。基于DDQN-ACO 算法得到的路径开销明显低于其他算法，与Manhattan-ACO 和DDQN-greedy 算法相比，本文所提算法在系统时间开销上分别提升了4.1%和16%。其次，在任务分配结果中可以看到每个UGV 被分配执行的任务序列起始点均为C，这表明每个UGV 都是由处理中心出发，最终将焦化厂内的污染土壤运输到处理中心，符合预期设定与实际运输流程。

表2 不同算法下的任务分配结果Table 2 Task assignment results under different algorithms

由算法的任务分配和路径规划结果（图5）可见，DDQN 训练的路径可以成功地避开障碍物和地势较高或较低的区域，最终找到相对平坦安全的路径。这是因为设计在DDQN 路径规划算法时考虑了地形因素对系统时间开销的影响，对UGV 行驶过程中碰到障碍物和高度差较大的区域时设置了较大的惩罚，经过一段时间的探索和训练，UGV 学习了这些规律，并最终形成平坦的路径。所以，与图5(d)相比，基于DDQN-ACO 算法获得的图5(b)的路径更平坦，减少了上坡和下坡情况。基于ACO 算法进行任务分配时，蚁群经过多次迭代保留最优分配策略，因此，与图5(f)相比，基于DDQN-ACO 算法的任务分配策略对应的各UGV 路径更加均衡。

通过表2 和图5 可以看出，相对于另外2 个对比算法，DDQN-ACO 算法获得的路径、任务分配策略和总开销均为最优。这是因为与Manhattan-ACO算法相比，DDQN-ACO 算法使用了从训练中获得的实际路径开销，这更接近实际的驾驶情况；与DDQN-greedy 算法相比，基于蚁群优化算法得到的任务分配策略比基于贪婪算法得到的任务分配更加均衡和高效。

在UGV 不同装载任务量的情况下DDQNACO 和另外2 种比较算法的系统时间开销如图6 所示。由图6 可以看出，随着UGV 装载任务量的增加，系统时间开销整体呈现降低趋势，这表明UGV 的装载任务量越大，单次能运输的污染土壤更多，有效地减少了往返处理中心的路径，节省了UGV 运输系统的时间开销，提高了运输效率。此外，与其他2 种算法相比，随着UGV 的装载量的变化，由DDQN-ACO 算法产生的系统时间开销始终保持最低。

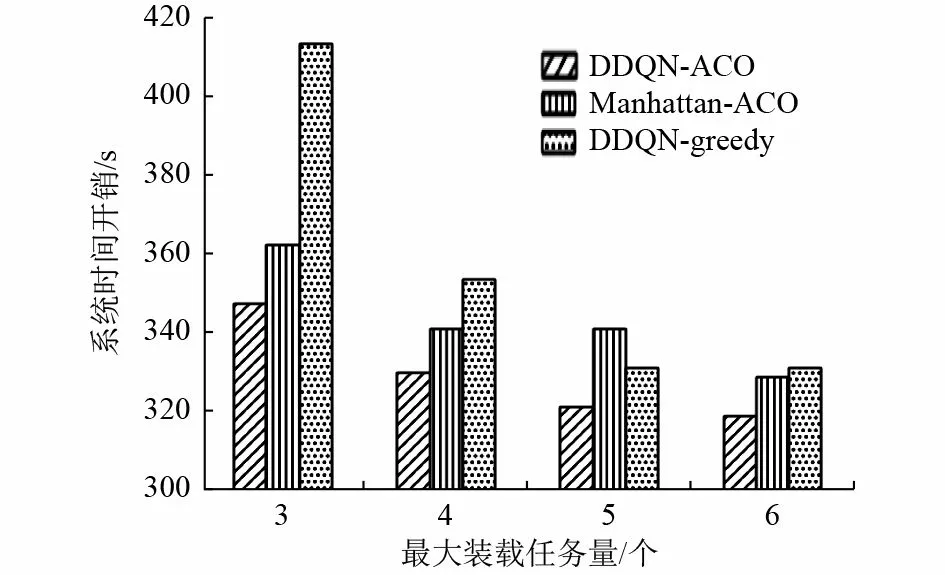
图6 不同UGV 最大装载任务量对系统时间开销的影响Fig.6 Impact of different UGV maximum loading tasks on system time cost

基于上述结果可以验证无人车在土壤污染环境中进行运输任务的可行性和高效性，结合已有研究利用无人车或智能机器人进行自动化工作的场景，如在码头装卸运输[26]、火车零件检测[27]、煤矿巡检运输[28]等，同样证明了利用无人车、机器人等智能设备能够节约人力成本，提高任务执行效率，可为行业带来更多的经济效益。

4 结论

（1）针对土壤污染场地中多智能无人车协同运输工作场景，综合考虑了土壤污染场地的地形地貌特点和无人车实际路径开销，设计了基于深度强化学习和蚁群优化算法的DDQN-ACO 算法，实现了集路径规划和协调调度为一体的多无人车运输系统。

（2）以提升土壤污染场地无人车系统时间开销为目标，在不同装载量情况下，提出的DDQNACO 算法与其他基于简单的线性距离或基于贪婪算法得到的任务分配策略相比，系统时间开销始终最低。