基于约束收敛法的Hoek-Brown 岩体巷道大变形分析
刘洪磊,张权云,关 凯,朱万成,于庆磊
(东北大学资源与土木工程学院,辽宁 沈阳 110819)
0 引言
近年来,在巷道开挖过程中,伴有衬里开裂甚至坍塌的大变形,对巷道施工过程中的安全构成了重大威胁,特别是在高地应力条件下,深部软岩巷道的大变形如帮壁膨出、底鼓等问题愈发突出,因此,从工程实际方面,需合理预测大变形条件下圆巷围岩力学响应,为围岩稳定性评估提供理论参考。而在理论分析方面,约束收敛法的原理是根据围岩特征曲线与支护特征曲线相交,得到的交点即为围岩与支护相互作用达到平衡时的应力与位移,由于巷道支护的目的是限制巷道位移量,因此结合工程经验,可为深部软岩巷道初期支护设计提供理论参考。而围岩特征曲线可通过圆形巷道的弹塑性解得到,因此合理预测巷道变形和围岩塑性区对支护优化设计和围岩结构稳定性有重要影响。同时采用不同的理论分析与不同破坏准则计算的巷道围岩应力状态与位移分布可能会存在不同程度的差异。选择合适的屈服准则和适用于深部实际巷道工程施工的分析方法进行深部软岩巷道的变形机理研究对于深部巷道支护设计具有重要意义。
长期以来,国内外已有众多学者对围岩弹塑性分析开展了大量有关小变形理论分析与大变形理论分析的研究。许多学者基于小变形理论,采用约束收敛法对围岩的变形特征展开研究[1-6],尽管小变形理论很简单,但是由于在建立控制方程时忽略了物质点的变化,因此在预测巷道施工后的岩体行为方面存在缺陷。特别是在高地应力条件下,可能会高估围岩变形能力,有时甚至会导致预测的变形大于开挖半径[7]。目前,地下金属矿山的开采深度逐渐增加,而小变形理论通常适用于浅层、硬岩的环境条件,但深部岩石地下工程具有高地应力、高温和高渗透水压等复杂的环境条件,岩土材料具有几何非线性特征,因此,小变形理论体系在深部岩石地下工程中不再适用。
近年来,针对上述缺陷,对深部巷道开挖的围岩大变形分析的研究越来越多,例如VRAKAS[8]提出了基于Mohr-Coulomb 准则(以下简称“MC 准则”)和Hoek-Brown 准则(以下简称“HB 准则”)的应变软化岩体在大变形理论条件下的开挖圆形巷道的解析解,但其基于理想弹塑性模型,未考虑围岩应变软化模型。ZHANG 等[9]提出了应变软化岩体围岩特征曲线的大变形解析解,发现大变形理论得出的位移、软化区半径均小于小变形解析解,且其差异随着弹性模量的减小而增大。关凯等[10-11]在VRAKAS 研究的基础上,考虑了岩体应变软化行为,对MC 准则岩体中开挖圆形巷道后引起的围岩响应进行研究。相关研究大多基于围岩理想弹塑性或弹-脆-塑性岩体力学行为进行研究,且求得的解析解结构较复杂,而岩石的破坏过程实际上是强度与变形参数逐渐劣化直至消失的过程,因而无法准确反映深部巷道围岩变形特征。
同时,针对地下金属矿山,当前众多学者对深部圆巷围岩洞壁变形的理论解析解分析多采用MC 准则或HB 屈服准则[11-13],但是由于地下矿山复杂的节理岩体条件,基于考虑地质强度指标和节理赋存状态的HB 强度准则预测其变形和破坏特性具有适用性。在VRAKAS[8]研究基础上,利用塑性区半径对物质点当前坐标及位移进行无量纲转换,并考虑强度与变形参数劣化的过程,基于HB 屈服准则提出了一种简单的深部软岩大变形预测方法,并以理论方法和前常铜铁矿巷道(矽卡岩、破碎、膨胀)监测数据进行有效验证,在验证的基础上进行了参数分析,并基于不同变形理论条件下围岩特征曲线区别,针对软弱破碎岩体提出支护建议。
1 理论介绍和理论方法简述
1.1 理论介绍
在连续、均匀、各向同性、初始弹性的岩体中开挖一个半径为R0的圆形巷道,如图1 所示,且其在横断面上所受静水应力为σ0,岩体弹塑性交界处即塑性区半径为Rp,巷道内壁受内部支护力为σa。
对于以上的轴对称平面应变问题,当前状态下的应力平衡方程见式(1)。
式中:σr为岩体的径向应力;σt为岩体的切向应力。
但需注意在大变形分析时,上述应力平衡方程应建立在巷道的已变形构型上,而变形的描述应该在图1 中的围岩稳定后的巷道半径处。在该问题中对数应变可以准确地描述应变-位移关系,因此在当前极坐标条件下,计算径向应变与切向应变的公式见式(2)和式(3)[8]。
当内部支护力逐渐减小时,围岩发生屈服,随着巷道开挖,围岩逐渐到达弹性极限状态,应力逐步达到岩石破坏的极限应力。而两种最常用的岩体破坏极限主应力间的关系有非线性HB 屈服准则和线性MC 屈服准则,此处采用的是HB 屈服准则,计算见式(4)。
式中:σ1为岩体的最大主应力,因本文研究轴对称问题,其值等于切向应力 σt,MPa;σ3为岩体的最小主应力,等于径向应力 σr,MPa;σci为完整岩体的单轴抗压强度,MPa;m为岩石的无量纲经验参数,反映岩石的软硬程度;s、a为无量纲材料常数。
在岩体发生屈服后,岩体强度突然下降,并遵循屈服后的软化行为。根据双线性函数计算应变软化岩体的强度和变形参数,见式(5)和式(6)。
在大变形分析中,有限变形理论给出的应力、应变在Eulerian 和Lagrange 两种坐标系下的转换关系有利于非线性方程的求解。同时,通过有限变形理论分析大变形问题时,采用基于变形率张量加性分解的次弹塑性模型进行求解,可得出类似于小变形理论的本构方程及塑性流动法则,见式(7)。需注意,上述方程均针对变形后的当前构型,且后文中的计算过程中应用的本构方程与塑性流动法则参考式(7)[11]。
式中:C为四阶弹性张量;σ为Cauchy 应力张量;Q为塑性势函数;ε为应变张量;λ为塑性乘子。
相较于之前的小变形分析[1-3],首先采用有限变形次弹塑性理论,不同于建立在变形前的初始构型上的小变形分析,应力边界和平衡方程均建立在已变形结构上;随后定义无量纲当前位置与无量纲位移,见式(8)和式(9),方便对数应变、圆环内任一点物质点处的半径与位移的无量纲变换,简化后续理论推导。
1.2 方法简述
利用有限差分方法,将塑性区(包括塑性软化区和残余区)划分为一组同心圆环(图2),其中,ρ(j)和ρ(j+1)为第j环内外边界的无量纲半径;j=1和j=n+1分别为对应于弹塑性边界和巷道洞壁;εrRp和 εtRp分别为弹塑性边界处的径向应变和切向应变。因此,σrRp、σt和 εrRp、εtRp等于初始值 σr1、σt1和 εr1、εt1。假设每个塑性区圆环的径向应力增量 Δσr都是恒定的,可通过式(8)计算。
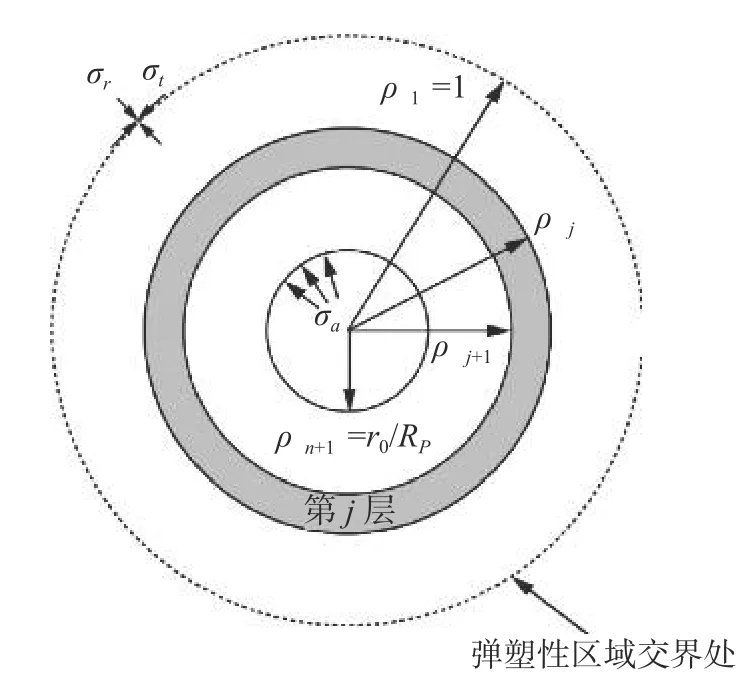
图2 塑性区划分圆环Fig.2 Concentric annulus in plastic zone
式中:n为划分的同心圆环总数;σr(j)为在r=r(j)(j=2,3,...,n+1)处的径向应力。
同时,为了便于后续理论推导和数值编程,定义了物质点无量纲当前位置及无量纲位移,见式(9)和式(10)。
当第j个塑性圆环足够小时,可假设无穷小圆环内岩体内径、外径受力近似与脆塑性岩体响应相同,如图3 所示。据此进行解析解推导时可将弹脆塑性岩体内径、外径所受径向应力 σa和 σRp分别用 和代替,弹塑性交界物质点处半径Rp和巷道开挖变形后半径a分别用 ρ(j)和 ρ(j+1)代替,且第j个塑性圆环可视为均质圆环,即第j环内任意物质点的力学性质均看作与 ρ=ρ(j)处的受力情况相同。

图3 第j 个圆环受力分布图Fig.3 Stress distribution in j annulus
根据式(8)中的塑性圆环各物质点分布规律,ρ(j+1)处物质点的径向应力计算见式(11)。
若划分的圆环数目足够多,即n值足够大,则第j个塑性圆环内岩体的径向和切向应力的解析式可参考VRAKAS 等研究的HB 岩体的理想弹塑性应力解析表达式[8]求得。
2 理论验证
VRAKAS 等[8,14]推导出基于HB 准则和MC 准则,圆形巷道软弱围岩的理想弹塑性大变形理论解析解,而基于以上研究,提出了大变形理论下,基于HB 破坏准则的巷道应变软化数值解法。为了能与VRAKAS等的理想弹塑性结果进行对比,采用临界塑性内变量值为0.000 01 与10 000,使研究退化为弹脆塑性问题和理想弹塑性问题。相关计算参数[5]:r0=2、μ=0.3、mp=1.7、sp=0.003 9、mr=0.85、sr=0.001 9、E=5.7 GPa、Ψp=0、Ψr=0、σcip=30 MPa、σcir=25 MPa、ap=0.55、ar=0.6、σ0=15 MPa。计算得出与VRAKAS 等[14]弹脆塑性和理想弹塑性对比结果,如图4 和图5 所示(VRAKAS结果用折线图表示,本文研究结果用散点图表示)。由图4 和图5 可知,结果能够很好地吻合,表明提出的大变形解析解能有效预测围岩挤压响应。

图4 理想弹塑性岩体结果对比Fig.4 Comparison of ideal elastic-plastic rock mass results

图5 弹脆塑性岩体结果对比Fig.5 Comparison of elastic brittle plastic rock mass results
3 前常铜铁矿巷道变形预测应用
为便于分析,以前常铜铁矿-480 m 中段试验巷道为例进行挤压巷道围岩变形预测应用探究,通过岩体基本参数计算理论推导条件下的松动圈、收敛位移以及损失位移大小,进而与监测数据对比来验证提出模型和方法的有效性与准确性。根据图6 所示近似方形的巷道断面尺寸为2.5 m×2.5 m,若将巷道视为等效圆形,可以得到巷道初始设计等效半径为1.25 m。

图6 -480 m 试验巷道初始设计断面Fig.6 Initial design cross-section of -480 m test tunnel
根据过往的研究[15-16]可知,岩体的峰后本构模型取决于岩石类型及地质强度指标GSI:对于较完整脆性岩体(GSI>75),岩体力学行为一般表现为弹脆塑性行为;对于中等节理岩体(25<GSI<75),岩体一般表现为应变软化行为;对于破碎岩体(GSI<25),岩体本构模型通常表现为理想弹塑性本构模型。由于试验巷道围岩主要为矽卡岩,根据有关矽卡岩强度和膨胀变形机制的研究可知,试验巷道围岩的矽卡岩大部分属于软岩,因此可采用应变软化模型(图7)研究矽卡岩巷道开挖的力学响应。根据ZHANG 等[6]研究,此时临界塑性内变量ηc的取值为0 与无穷大之间(在分析中以ηc=0.114 1 进行等效计算)。

图7 应变软化模型Fig.7 Strain softening model
前常铜铁矿-480 m 中段试验巷道断面尺寸、原岩应力及矽卡岩力学参数见表1。值得注意的是,在分析时假设施加的支护措施相对于变形压力可以忽略不计,即巷道开挖后支护结构均发生完全毁坏σσ=0;此外,静水原岩应力大小采用自重应力γh进行计算,其中,γ和h分别为岩体容重和埋深,即σ0为12.48 MPa。同时,为了确保数值结果的精确度在可控范围内,弹性区物质点数ne以及塑性区物质点数np均取100,计算容差Tol=1e-7。
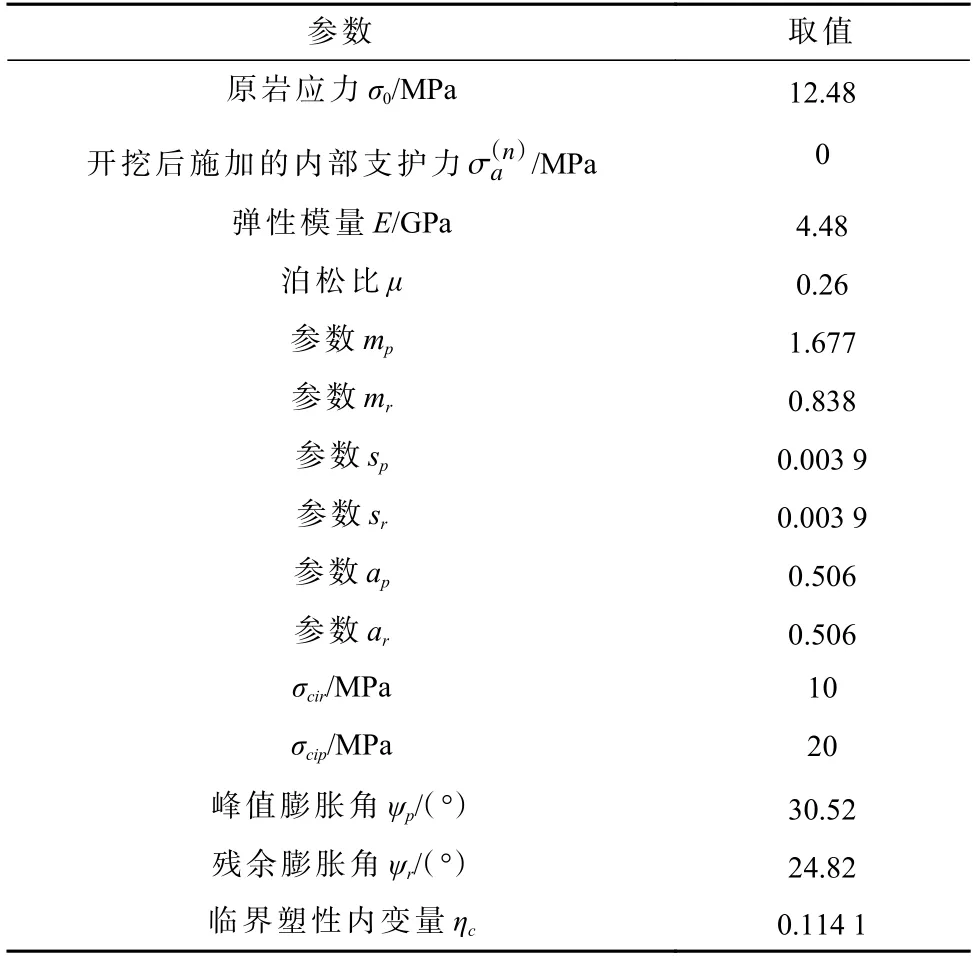
表1 -480 m 中段试验巷道相关计算参数Table 1 Calculation parameters related to the -480 m middle section test tunnel
于庆磊等[17]、褚吉祥等[18]对-480 m 巷道分别进行了矽卡岩松动圈和巷道最大收敛变形的现场测量,为了验证提出方法的准确性,将现场监测结果值与提出的理论模型数值结果进行对比验证。巷道初始设计半径为a0=1.25 m,表2 为计算结果与矽卡岩巷道现场监测(探测)结果的对比。

表2 巷道开挖大变形理论与现场监测结果对比Table 2 Comparison of the tunnel excavation based on the large deformation theory and field monitoring results
由表2 可知,基于理论分析得到的塑性区大小(3.14 m)位于现场监测松动圈范围(2.5~3.8 m)之内,且平均相对误差仅为0.32%。而在巷道收敛变形预测方面,理论计算结果(76.00 mm)远大于现场监测结果(48.00 mm),且平均相对误差高达58.3%;由于理论计算得到的巷道收敛变形为巷道开挖扰动引起的总变形量,而现场监测的收敛变形仅是在多点位移计安装之后的部分位移,使得在设备安装之前发生的围岩位移监测不到(图8),这部分位移也称损失位移,其可通过超前钻孔测量或基于巷道纵向变形曲线等理论方法获得,因此造成收敛变形的理论计算结果远大于现场监测值。
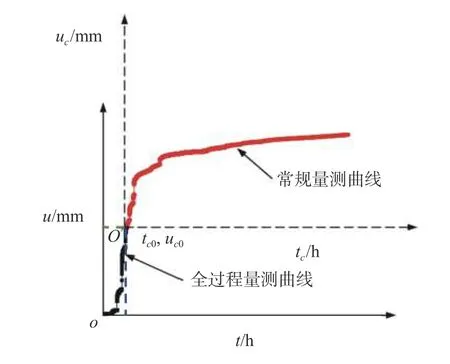
图8 损失位移概念图Fig.8 Loss displacement
根据表2 可以反演出多点位移计安装前围岩的损失位移为28 mm。由此可知,考虑到多点位移计监测收敛变形的局限性以及基于理论模型得到的巷道塑性区与实测松动圈范围基本一致,可以认为研究提出的理论方法是正确有效的,能较好地预测大变形应变软化围岩巷道的开挖响应。
4 岩体参数分析
4.1 强度参数a 对广义HB 岩体弹塑性解的影响
研究提出的有限差分方法中所有的强度参数均可通过塑性内变量求出(式(6))。但是HOEK 等[16]研究得出,在HB 破坏准则中,强度参数a不再是固定的0.5,而是随着地质条件变化,经验关系见式(12)。
式中,GSI为反映岩体断裂面状况的地质强度指数,GSI的范围为10~100,故a在0.5~0.6 之间变化。因此,为了正确使用该准则,需分析强度参数a是如何影响弹塑性行为的。
采用以下参数研究强度参数a对围岩特征曲线和应力位移分布曲线的影响:r0=2 m、μ=0.3、mp=1.7、sp=0.003 9、mr=0.85、sr=0.001 9、E=5.7 GPa、Ψp=0°、Ψr=0°、σcip=30 MPa、σcir=25 MPa、ap=0.55、ar=0.6、ηc=0.004、σ0=15 MPa。图9 为假设的不同强度参数a条件下的四种应力及位移分布图。其中三条曲线假设强度参数a的残余值和峰值分别为0.50、0.55、0.60,而其中一条曲线假设参数a随着临界塑性内变量 ηc从0.50 到0.60 变化,其他输入数据保持不变。由图9 可知,当内部支护力 σa很小时,图中的曲线差别较大,且ap与ar不等时,曲线更接近ap=0.60 时的围岩特征曲线,这说明峰值强度参数对结果影响更大;而a值较大时,塑性区半径也大,如图10 所示,说明峰值强度参数对塑性区半径也有一定影响。从图9 还可以看出,a值越大洞壁收敛位移也会越大,而由图11 可知,ap=ar=0.60 是其等于0.50 位移的三倍,故HB 准则中的强度参数a值对岩体开挖响应的影响相对较大,同时a值越大岩体更易破坏。

图9 参数a 对应力及位移分布的影响Fig.9 Influence of the parameter a on the stress and displacement distribution
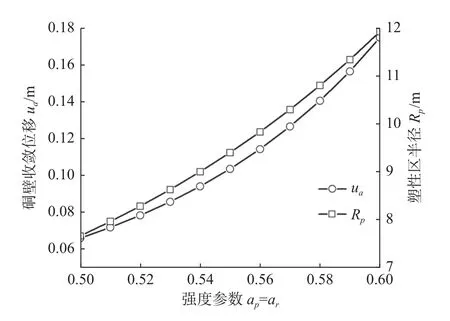
图10 洞壁收敛位移、塑性区半径与强度参数a 的关系曲线Fig.10 Relationship curves of cave wall convergence displacement,plastic zone radius and strength parameter a
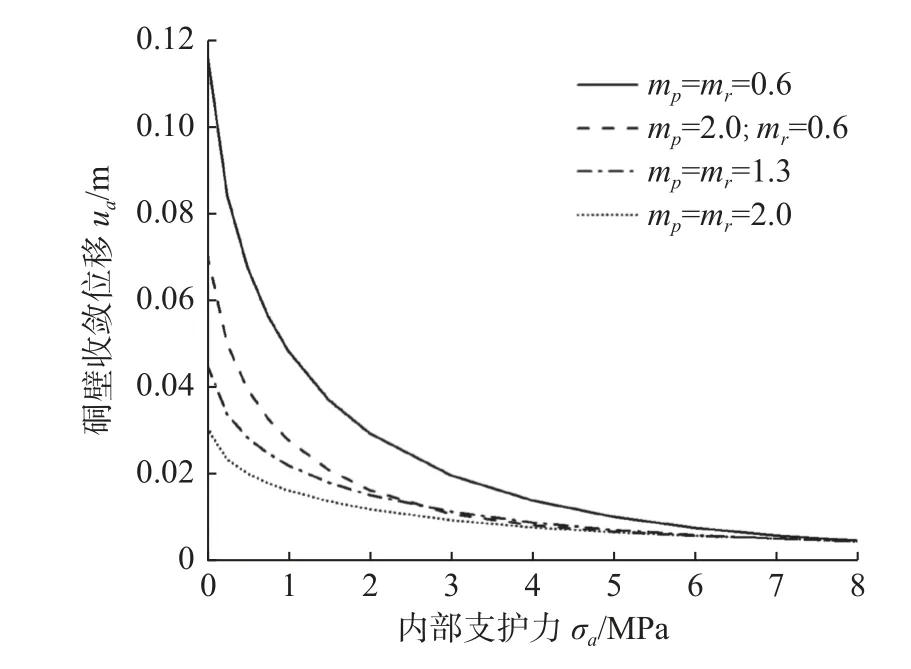
图11 参数m 对围岩特征曲线的影响Fig.11 Influence of parameter m on the characteristic curve of surrounding rock
4.2 强度参数m、s 的影响
HOEK 等[16]提出强度参数m、s也与地质强度指标GSI相关,可通过经验公式计算,见式(13)和式(14)。
式中:D为应力释放或爆炸破坏对岩体扰动程度的系数;mi为组成岩体的完整岩块的Hoek-Brown 常数;m、s为岩体的强度常数,其中,m为岩石的软硬程度,其取值范围为0.000 000 1(严重扰动岩体)~25(理想完整的坚硬岩体);s为岩体破碎程度,其取值范围为0(极破碎岩体)~1(理想完整岩体)。地质强度指标GSI与岩体的表面粗糙性和表面风化程度、结构特征等特征有关。因此,强度参数m和s能够综合反映岩体结构、岩矿状态和岩体不连续面质量,为了准确分析岩体质量与强度参数的变化关系,从而正确使用该准则,还需分析强度参数m、s是如何影响弹塑性行为。
为了探讨强度参数m对围岩特征曲线的影响,绘制参数m对围岩特征曲线的影响曲线图,如图11所示。由图11 可知,随着强度参数的增大,相同内部支护力条件下的位移对应减小,说明m越大岩体强度越高,而且围岩特征曲线的增幅与强度参数的增幅不同,相同内部支护力条件下的位移增幅明显更大,强度参数在0.6、1.3、2.0 值时随着强度参数的增大,位移逐渐减小且减小速度快,而在内部支护力值大于8 时,位移与塑性区半径增加速度逐渐平缓。因m反映岩石的软硬程度,m越大岩体越完整坚硬、岩体内的节理裂隙越少,以上变化规律说明软岩对围岩特征曲线、位移及塑性区半径的影响较大,而硬岩对位移及塑性区半径几乎没有影响,即相对较硬的岩体经开挖产生的洞壁收敛位移与塑性区半径相对较小。
同时强度参数s对围岩特征曲线、位移及塑性区半径的影响和强度参数m的影响类似,如图12 和图13 所示。由图12 和图13 可知,相对破碎岩体产生的位移及塑性区范围比相对完整岩体的位移及塑性区范围更大。同时相比于强度参数m,岩体力学行为对强度参数s更敏感。
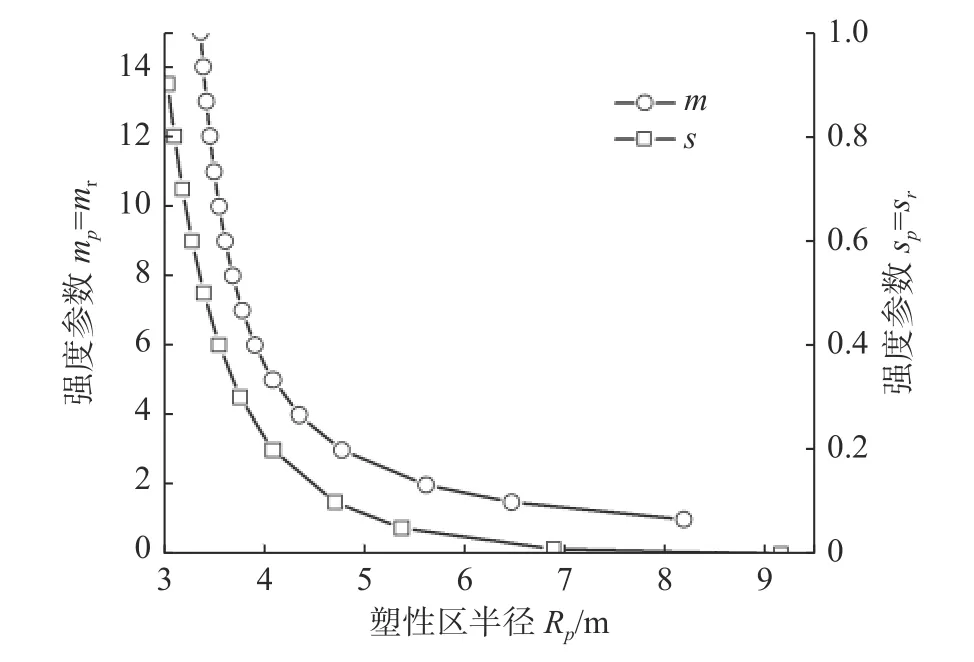
图12 强度参数m、s 对塑性区半径的影响曲线Fig.12 Influence of parameter m、s on the plastic zone
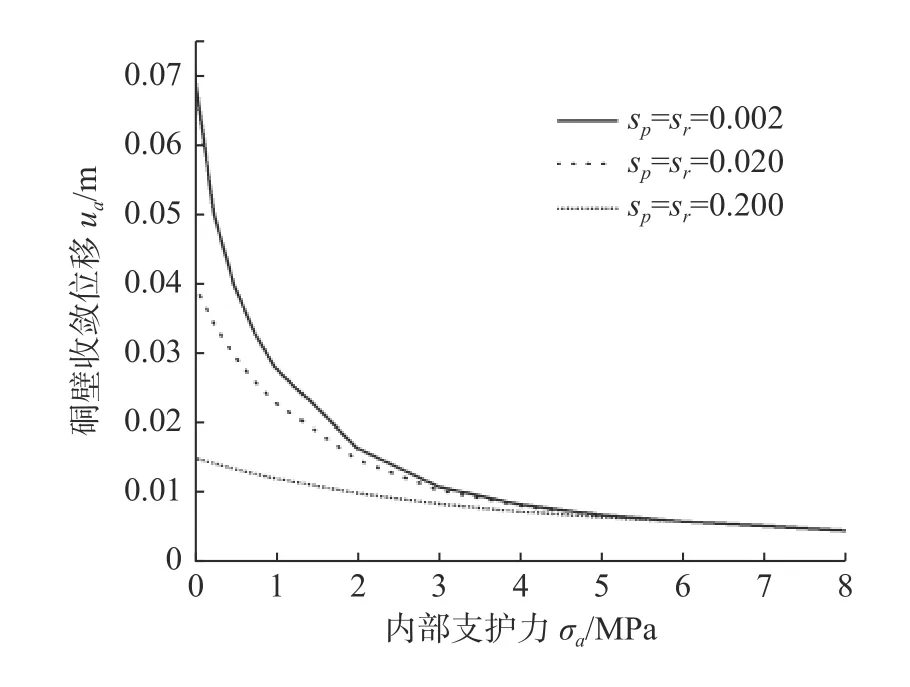
图13 参数s 对围岩特征曲线的影响Fig.13 Influence of parameter s on the ground curve
4.3 临界塑性内变量的影响
理想弹塑性和弹脆塑性是岩体力学行为的两种特殊情况,通过调节临界塑性内变量的数值大小,使得岩体基本力学参数在峰值参数与残余参数之间变化,从而达到两种特殊状态。为了直观体现不同临界塑性内变量对岩体巷道开挖响应的影响,选取岩体基本力学参 数:r0=3 m、μ=0.25、mp=2、sp=0.004、mr=0.6、sr=0.002、E=5.7 GPa、Ψp=1.55°、Ψr=1.55°、σcip=30 MPa、σcir=25 MPa、ap=0.506、ar=0.530、ηc=0.01、σ0=15 MPa、σa=0.75 MPa,绘制了应力分布、洞壁收敛位移与临界塑性内变量的关系曲线,如图14 和图15所示。由图14 可知,随着临界塑性内变量的增大,应力、塑性区半径以及收敛位移均在不断减小,因此不同的临界塑性内变量值将导致巷道围岩塑性区应力分布的不同。由图15 可知,在应变软化阶段,临界塑性内变量的轻微降低将会引起较大巷道围岩变形及洞壁位移增量,同时,临界塑性内变量约大于0.1 或临界塑性内变量约小于0.001 时,洞壁收敛位移趋于平缓,此时临界塑性内变量几乎没有影响,说明此时比较接近岩体力学行为的两种特殊情况——弹脆塑性与理想弹塑性本构模型。
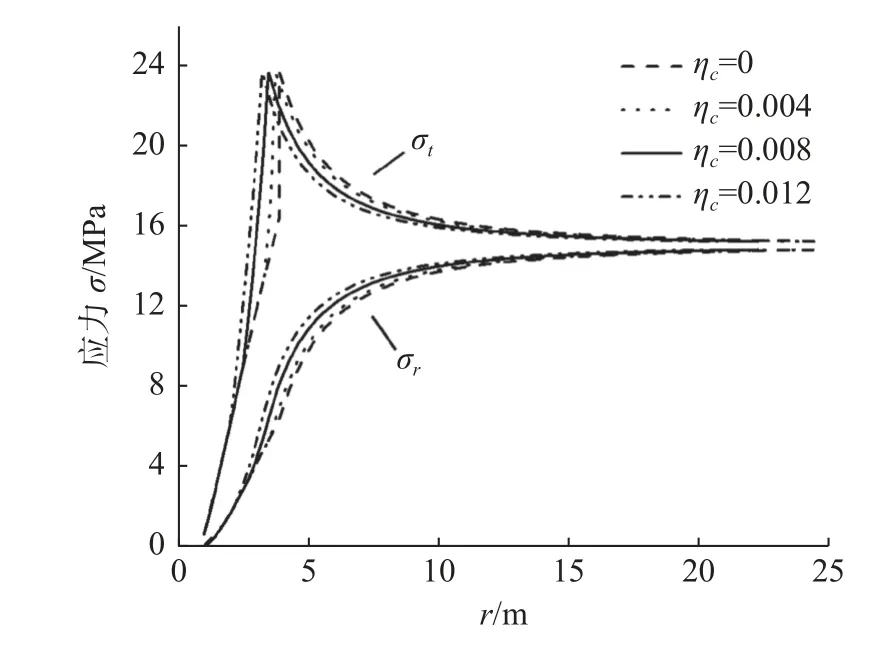
图14 临界塑性内变量对应力分布的影响Fig.14 Influence of critical plastic internal variables on stress distribution

图15 洞壁收敛位移与临界塑性内变量的关系图Fig.15 Relationship between wall convergence displacement and critical plastic internal variables
4.4 小变形和大变形理论下的围岩响应
在围岩与支护耦合作用中,收敛约束法是以巷道开挖后围岩弹塑性理论为基础、参考现场监测数据、结合工程经验判断的支护设计方法,其主要由围岩特征曲线和支护特征曲线组成[11,19]。为了探讨不同理论方法对工程施工过程中巷道围岩变形预测及支护受力分析的影响,基于约束收敛法,根据不同分析方法即大变形与小变形理论及破坏准则,研究不同条件下的围岩特征曲线的区别。
根据约束收敛法,图16 为采用不同变形理论及破坏准则条件下的围岩-支护相互作用曲线。当在大变形理论分析中,采用MC 破坏准则时,围岩特征曲线与支护特征曲线相交于图中C 点处,表明支护与围岩平衡时的支护所受压力为σaC;如果在大变形分析中,采用HB 破坏准则,则此时围岩特征曲线在弹性阶段的应力与位移与MC 准则的基本一致,而在塑性阶段,相同洞壁收敛位移条件下,支护压力反而较小,与支护特征曲线相交于D 点;同时当采用小变形理论分析MC 岩体圆形巷道开挖时的围岩响应,围岩与支护特征曲线在A 点相交,此时会高估巷道围岩的挤压势;而当采用小变形理论分析HB 岩体巷道开挖时,两曲线相交于B 点,由图16 可知,对于分析方法,大变形理论明显比小变形理论结果更准确预测围岩变形,而针对破坏准则分析,HB 破坏准则明显比MC 破坏准则更准确。因HB 准则预测节理岩体更准确,因此基于HB 准则的大变形计算方法更准确,但在深部软岩巷道开挖的高地应力赋存条件下,为了防止因提供的支护力不足导致围岩-支护整体结构失稳,采用基于MC 准则的大变形理论进行支护设计既节约成本又可为支护结构破坏预留一定压力。
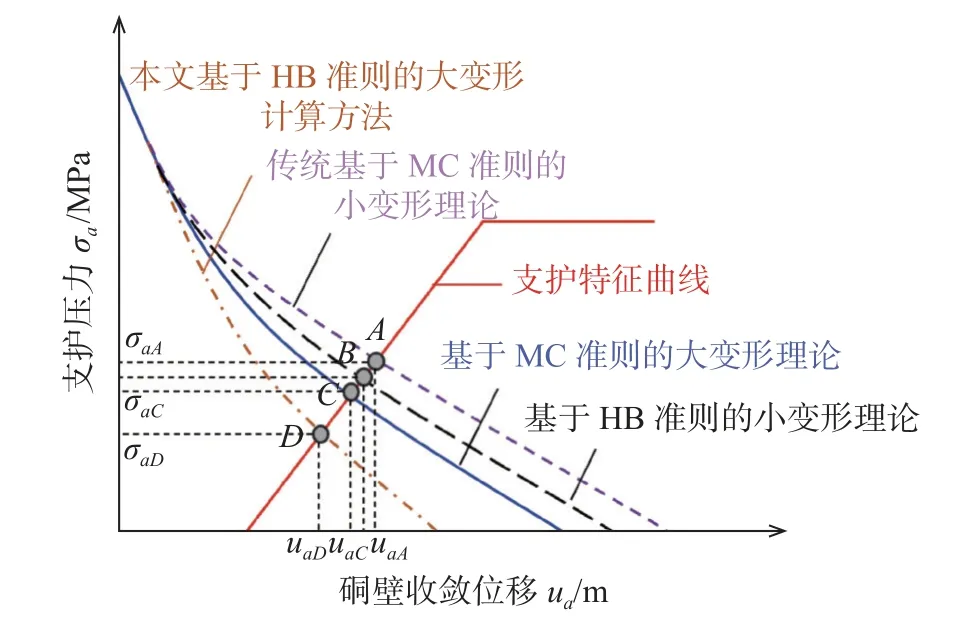
图16 挤压岩体围岩-支护相互作用曲线Fig.16 Interaction curve of surrounding rock-support of extruded rock mass
5 结论
在VRAKAS 等[8,14]研究的基础上,采用Hoek-Brown 破坏准则,提出了针对圆形巷道软弱围岩应变软化条件下的大变形理论方法,研究了m、s、a等不同强度参数对围岩响应的影响,并基于约束收敛法通过大变形与小变形理论分析结果对比,为支护设计提供分析手段和建议,得到结论如下所述。
1)根据平衡方程、Hoek-Brown 破坏准则等提出相对简单的应变软化大变形分析方法。
2)通过理想弹塑性和弹脆塑性理论结果对比以及工程实例中的松动圈以及收敛位移大小对比验证本文提出模型和方法的有效性与准确性。
3)研究了不同强度参数及理论方法对围岩响应的影响:随着强度参数m、s逐渐增加,巷道围岩的位移及应力逐渐减小,而强度参数a的影响相反。大变形与小变形理论方法条件下的围岩特征曲线对比,说明采用大变形分析方法,所得支护压力与收敛位移相对更小,结果更准确;而MC 准则比HB 准则所得洞壁收敛位移更小,结果更准确,但在高原岩应力条件下,则很可能由于支护提供的压力不足以抵抗围岩破坏从而导致支护结构发生破坏或巷道失稳,故基于MC 准则的大变形理论预测的支护效果相对HB 准则更偏于保守。

