基于模糊PID的箱梁移动焊接机器人*

吴泽华,张 霖,王宝玉,赵言正

(1.上海交通大学机械与动力工程学院,上海 200240;2.浙江理工大学机械工程学院,杭州 310018)

0 引言

结构化钢箱梁结构在现代公路桥梁等基础设施建设中得到广泛应用[1]。箱梁结构的质量和焊接工艺性能对于桥梁的施工质量非常关键。移动作业机器人可以代替人工完成箱梁的焊接作业,提升箱梁焊接作业效率及其自动化程度。箱梁内部复杂的环境以及机器人移动作业较高的运动控制精度要求增加了各方面的技术难度[2-4]。

为了保证移动机器人具有较高移动速度和环境适应能力,目前大多数移动机器人均采用轮腿式[5-6]、腿履式[7-8]复合移动机构。加州理工学院的Paolo Fiorini为适应行星探测的复杂地形,设计了一系列的轮足式移动机器人[9];王妹婷等[10]针对高层建筑玻璃清洗要求,设计了一种基于PD控制的轮腿式壁面清洗机器人;罗洋等[11]设计了一种采用自适应控制算法的轮腿式机器人;孟凡军等[12]为了提高机器人越障的稳定性与可靠性,提出了基于多DSP的轮腿式机器人控制系统;罗庆生等[13]研制的新型轮腿式机器人,采用了人机交互系统和嵌入式控制系统;陈斌等[14]基于自适应模糊PID控制的四足机器人;SIEGWART等[15]设计了一种六足轮腿式全地形机器人,该机器人具有良好的被动爬行能力。

本文为实现箱梁移动焊接作业的目标,设计了一种新型轮腿复合式移动焊接机器人,相较于传统的轮式或者腿式作业机器人,该机器人具有更强地形适应能力和更高的移动速度,同时结合模糊控制算法与PID控制方法设计了模糊PID控制器,最后通过仿真以及实验验证了相较于普遍使用的PID控制算法,基于模糊PID控制的轮腿式机器人能够实现更高精度的直线运动,证明了本文所提出控制算法的有效性和优越性。

1 移动机器人结构设计与分析

1.1 移动机器人结构设计

本文提出的轮腿式移动机器人是由1个长方体机体和6个结构相同的轮腿结构组成,如图1所示。

图1 移动焊接机器人整体结构图

该机器人6条腿对称分布于机体两侧,每条腿有3个转动副,1个移动副。该机构结构相对简单,运动学模型容易建立,有利于机器人的步态规划和实时控制。

1.2 腿部结构设计

本文设计的轮腿结构如图2所示。该轮腿结构主要由升降柱、连杆1、连杆2、轮足组成,共有1个移动关节,2个转动关节。首先,升降柱与机体固联,移动关节位于升降柱上,实现机器人腿部的升降动作;然后,升降柱与连杆1通过转动关节1相连,连杆1与连杆2通过转动关节2相连;最后,轮足安装在连杆2的末端,通过电机驱动,实现平面滚动。

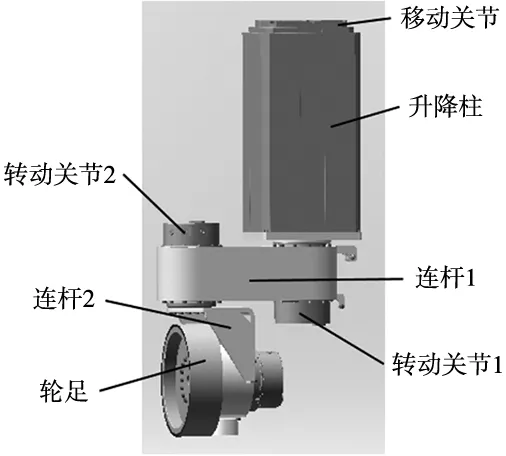
图2 单腿结构模型

2 运动学分析

2.1 腿式运动学分析

考虑到机器人运动过程中需要完成越障运动,则需要将足端轮子锁死,此时机器人相当于足式移动机器人。为了不失一般性,需要对上述模型进行简化,然后根据简化后的单腿结构,利用改进D-H参数法建立单腿各关节坐标系(符合右手原则),如图3所示。

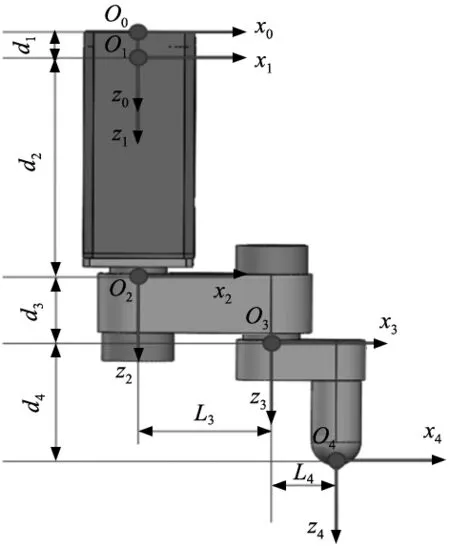
图3 单腿D-H坐标系

坐标系O1与坐标系O0在x-z平面内共平面,坐标系O2与坐标系O1在x-z平面内共平面,坐标系O3与坐标系O2在x-z平面内共平面,坐标系O4与坐标系O3在x-z平面内共平面。单腿的D-H参数如表1所示。

表1 单腿D-H参数

表中,d2、d3、d4、L3、L4均为常数,d1、θ2、θ3为关节变量。

相邻坐标系变换矩阵:

(1)

将单腿D-H参数代入得坐标系O0到坐标系O1的齐次变换矩阵:

(2)

将单腿D-H参数代入得坐标系O1到坐标系O2的齐次变换矩阵:

(3)

将单腿D-H参数代入得坐标系O2到坐标系O3的齐次变换矩阵:

(4)

将单腿D-H参数代入得坐标系O3到坐标系O4的齐次变换矩阵:

(5)

最终可以得出从机器人执行末端坐标系O4到起始坐标系O0的总变换矩阵为:

(6)

由此得到机器人单足运动学正解。其中:

r11=cos(θ2+θ3)
r12=-sin(θ2+θ3)
r13=0
r21=sin(θ2+θ3)
r22=cos(θ2+θ3)
r23=0
r31=0
r32=0
r33=1
px=L4cos(θ2+θ3)+L3cosθ2
py=L4sin(θ2+θ3)+L3sinθ2
pz=d1+d2+d3+d4

2.2 轮式运动学分析

在箱梁内部地面移动时,由于地面较为平整,可以利用电机驱动足部轮滚动来实现机器人的移动,提高机器人的移动速度。考虑到降低控制的复杂性,可以将机器人简化为轮式机器人,并建立坐标系进行运动学分析,如图4所示。

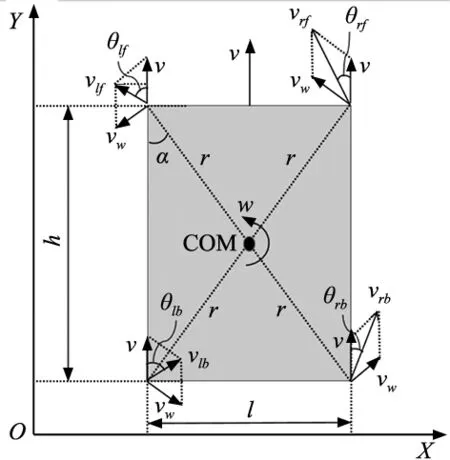
图4 轮式运动学分析图

考虑到机器人本体结构完全对称,故以底盘几何中心COM为质心,机器人的运动速度可以分为沿前进方向上的线速度v和绕底盘质心COM作圆周旋转运动的角速度w,其中vlf与θlf,vrf与θrf,vlb与θlb,vrb与θrb分别为左前轮、右前轮、左后轮、右后轮的速度大小与方向角,因此可知:

vw=wr

(7)

(8)

(9)

根据图4所示几何关系可知vlf为线速度v和角速度vw的合成速度,因此:

vlfx=vwcosα

(10)

vlfy=v-vwsinα

(11)

式中:vlfx为vlf沿x轴方向的分量,vlfy为vlf沿y轴方向的分量。

根据图4所示几何关系,利用勾股定理和三角函数,可求得:

(12)

(13)

同理,可求得:

vrfx=vwcosα

(14)

vrfy=v+vwsinα

(15)

vlbx=vwcosα

(16)

vlby=v-vwsinα

(17)

vrbx=vwcosα

(18)

vrby=v+vwsinα

(19)

式中:vrfx为vrf沿x轴方向的分量,vrfy为vrf沿y轴方向的分量,vlbx为vlb沿x轴方向的分量,vlby为vlb沿y轴方向的分量,vrbx为vrb沿x轴方向的分量,vrby为vrb沿y轴方向的分量。

(20)

(21)

(22)

(23)

(24)

(25)

3 越障步态规划

在兼顾效率和稳定性情况下,六足机器人步态按同时支撑的腿数可以分为2种:三足支撑步态、四足支撑步态。考虑六足轮腿式机器人可以通过足部轮滚动实现在平地上移动,而在越障时采用足式与轮式相结合的运动模式,故采用四足支撑步态。如图5所示,步态流程为:

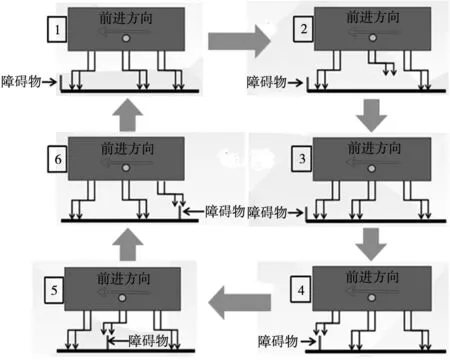
图5 越障步态流程图

步骤1:开始越障前,将中部两腿立足点朝前进方向调整,保证重心垂直投影落在中部左右两腿和后部左右两腿立足点构成的四边形支撑区域内部;

步骤2:然后是前部左右两腿开始越障,前部左右两腿同时抬起,再驱动支撑腿轮子滚动,机器人向前移动直到前部两腿越过障碍物,放下前部左右两腿;

步骤3:接着是中部左右两腿的越障过程,中部左右两腿同时抬起,再驱动支撑腿轮子滚动,机器人向前移动直到中部两腿越过障碍物,将中部两腿立足点朝后退方向调整,保证重心垂直投影落在前部左右两腿和中部左右两腿立足点构成的四边形支撑区域内部;

步骤4:最后是后部左右两腿的越障过程,过程如之前部两腿的越障步骤。

4 模糊PID控制算法及仿真

移动焊接机器人需要沿着箱梁的纵向轴线运动,运动的过程中可能会偏离轴线,故需要通过合理协调两侧轮间差速来调整机器人运动方向,确保其沿着预定路线进行运动。

本项目采用模糊PID控制技术来实现差速补偿。首先,将机器人实时运动方向与预定方向角度的偏差e和偏差变化率ec作为模糊PID控制器的输入,将PID控制器的3个参数kp、ki、kd作为输出,PID控制器将输出两侧轮组的差速补偿值,通过运动补偿保证在作业过程中机器人沿着箱梁的纵向轴线运动,避免机器人与箱梁产生碰撞的风险。模糊PID控制器结构如图6所示。

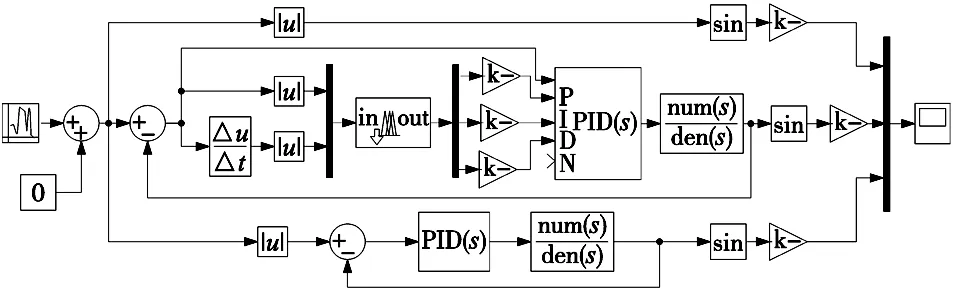
图6 模糊PID控制器结构框图

模糊PID控制首先确定其模糊集为{NB,NM,NS,ZO,PS,PM,PB},其隶属度函数为三角函数,然后建立模糊控制规则,如表2所示,再确定其输入输出的取值范围,e、ec、kp、ki、kd的论域均为[-3,3],比例因子设置为:Kkp=1,Kki=0.1,Kkd=0.4,模糊PID控制器的效果可以通过合理调节比例因子来实现调整。

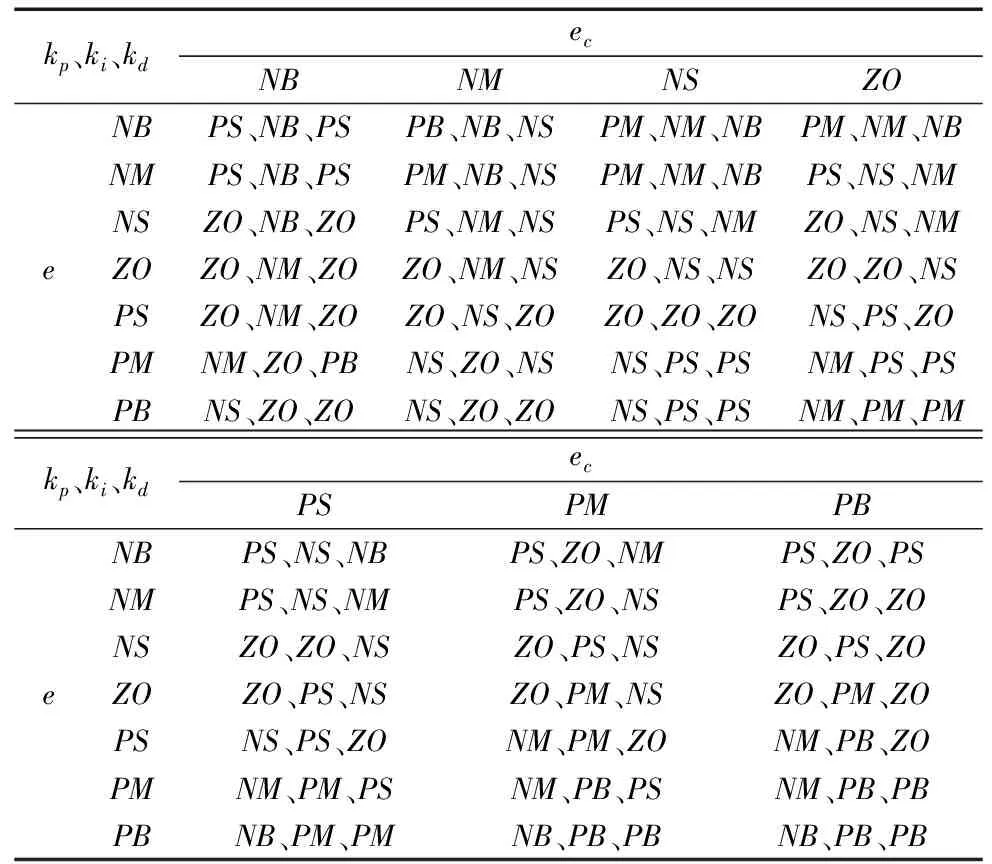
表2 模糊控制规则

设定移动焊接机器人在运动的过程中其运动方向发生随机性偏差,偏差角度范围大小为±1°,赋予移动焊接机器人15 mm/s的移动速度,仿真结果如图7所示。

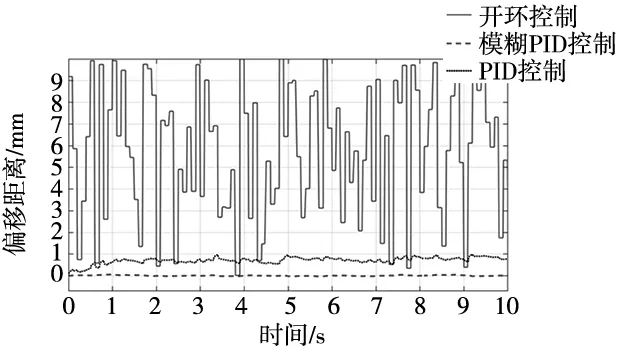
图7 仿真结果

根据仿真结果可知,当移动焊接机器人采用开环控制,其运动轨迹在随机偏差的影响下表现得非常不稳定且发生较大偏移,当移动焊接机器人采用普通PID控制时,其运动轨迹相较于开环控制发生的偏移更小,而采用模糊PID控制时,移动焊接机器人运动轨迹在随机偏差的影响下表现得非常稳定且偏移最小,故模糊PID控制是三者中最优的控制方案。在模糊PID控制实现差速补偿的情况下,移动焊接机器人基本可以沿着直线运动,能够保证移动焊接机器人在工作过程中具有较高的运动直线度。

5 实验

实验室条件下,控制移动焊接机器人沿着激光仪发出的垂直光线做直线运动,如图8所示,利用游标卡尺分别测量机器人在起点和终点到激光光线的距离,即可得到机器人运动过程中在预期方向上的实际偏差量。

图8 直线运动实验

根据位姿信息绘制出移动焊接机器人运动轨迹,如图9所示。实验过程中机器人的运动速度为10 mm/s,实际位置偏差测量结果如表3所示。

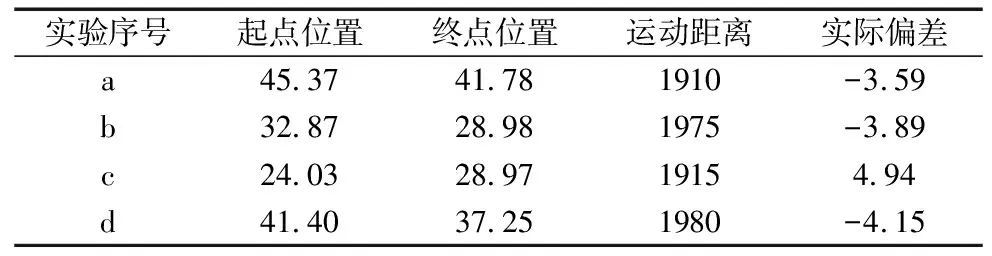
表3 实际偏差测量结果(mm)

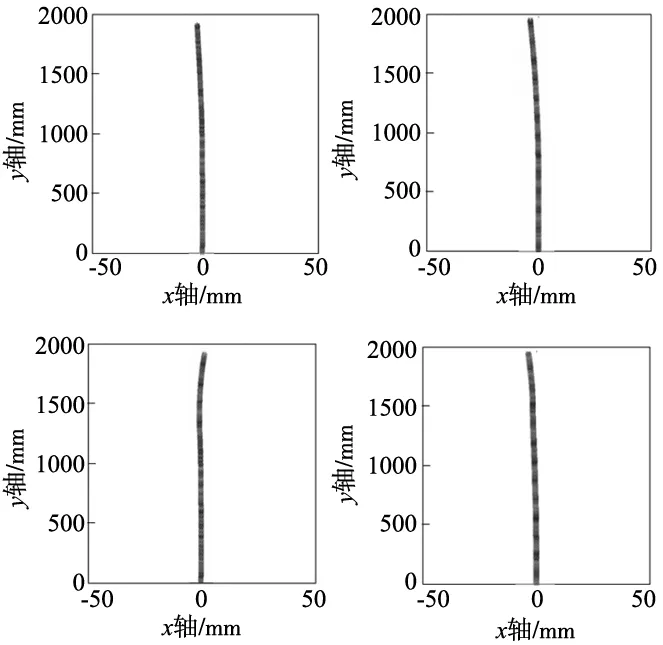
图9 直线运动轨迹

根据上述实验结果分析可知,移动焊接机器人在近2000 mm的直线运动行程中,不可避免地产生了直线度偏差,实际偏差值在±5 mm范围内,箱梁每个隔断门之间的平均长度为4000 mm,正常情况下移动焊接机器人沿箱梁纵向轴线运动的偏差量在±10 mm范围内,这样的运动精度满足预期的±40 mm移动作业偏差要求。

6 结论

针对箱梁内部的移动作业问题,本文提出了一种轮腿式移动焊接机器人,建立了机器人腿式和轮式的运动学模型,根据工作环境规划了机器人的运动步态,并设计了模糊PID控制器,仿真及实验结果表明,该控制方法相较于目前普遍使用的PID控制具有更高的直线运动精度,移动焊接机器人在近2000 mm的直线运动行程中,其实际偏差值保持在±5 mm范围内,满足预期的移动作业偏差要求,证明了该基于模糊PID控制的移动焊接机器人运动的稳定性与有效性。