基于PILCO架构的自适应内模控制器优化*
梁俊朗,高 健
(广东工业大学省部共建精密电子制造技术与装备国家重点实验室,广州 510006)
0 引言
随着微电子封装制造领域的快速发展,高速精密运动平台是封装制造装备的核心部件之一,其控制性能直接影响制造装备整体的精度、效率等性能指标的提升。为提高运动平台的精密运动控制性能,许多学者在精密运动控制算法上开展了深入研究[1-3]。目前,PID控制算法仍是工业界最为广泛的控制算法,常用的参数整定方法有Ziegler-Nichols(Z-N)方法,Cohen-Coon(CC)方法,内模控制法等,受研究对象的结构特性,复杂工况和非线性问题显著提升了控制的复杂性,使精准的PID参数调节更加困难。针对PID参数整定的难题,丁荣乐等[4]提出了一种基于离散时域等价性的自适应控制率,提高了有效载荷变化控制的鲁棒性,苏杰等[5]研究了一种基于自耦PID的控制方法,建立最速模型和绝对误差模型,有效避免积分饱和引起的超调问题,吴亚雄等[6]利用BP神经网络调节分数阶PID控制器,实时在线整定PID分数阶的5个参数,提高了并网电流的跟踪性能。因此,现有的控制方法可以结合研究对象各自的运动特性,实现PID参数的自适应调节。
然而,如何适应不同场合、运动条件和外载等变化,实现运动平台的控制参数最优快速调节,仍然面临着挑战。目前,人工智能已成为学术界和工业领域研究的热点,强化学习是人工智能领域重要分支之一,可根据复杂环境试错寻找最优策略。学者因此纷纷将强化学习用于不同领域,如将强化学习与传统控制相结合,在无人机控制[7-9]、机器人控制[10]、自动驾驶[11]等方面,取得了良好进展和成果[4]。强化学习分为有模型强化学习和无模型强化学习,一般而言,无模型强化学习的渐进性能优于有模型强化学习,但需要同外界环境进行多次交互,数据利用效率低,容易造成器械损耗,难以应用于实际机械控制中。有模型强化学习控制算法通过部分数据提前构建虚拟模型,在后续交互过程中不断修正模型,一定程度上提高了数据的利用效率。在实际应用中,有模型的强化学习具有更好的应用前景,其中,概率推理学习控制算法是一种经典的强化学习控制算法,利用高斯过程建立输入与输出之间的概率动力学模型,根据奖惩设置优化控制策略,提高收敛速度,已广泛应用于机器人控制。
传统PID调参方法一般需要建立特定的数学函数,难以保证控制方法的泛化性,而强化学习需要多次与环境交互,难以保证数据效率的有效性和收敛性,本文结合传统内模PID控制方法实现初步参数调节,保证强化学习二次优化的收敛特性和数据利用效率,基于 PILCO算法在线优化内模参数,实现传统控制方法和强化学习方法的有效结合,无需建立复杂准确的数学方程,降低调参难度,与内模PID控制器相比,所提方法具有更高的控制精度和任务泛化性能,因此,本文所提方法具有良好的先进性,可广泛应用于自适应精密运动控制领域。
1 精密运动平台的受力分析
1.1 系统硬件介绍
本文研究的高速精密运动平台结构如图1所示。主要由大理石基座、直线电机、运动平台及直线光栅等组成。运动平台与直线电机动子固连,光栅编码器安装于平台侧面,在平台运动过程中,直线电机驱动运动平台,光栅尺实时反馈运动平台位置信息,可针对性的设计智能闭环控制方法,实现平台的精准控制。
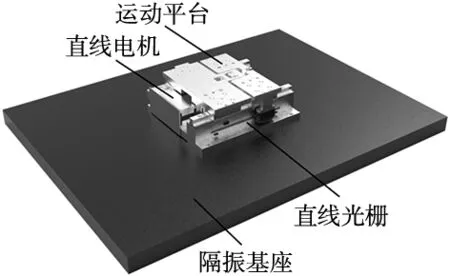
图1 精密运动平台结构示意图
1.2 运动平台动力学分析
根据上述结构对其进行刚柔耦合建模,将平台与导轨之间各种连接件的柔性环节考虑为等效弹簧,根据动力学模型将其等效为质量-弹簧-阻尼的二阶系统,如图2所示,K为系统的等效刚度,C为系统等效阻尼系数,M为整体运动部件的等效质量,F为直线电机驱动力,x为平台的运动位移。

图2 精密运动平台动力学模型
基于牛顿第二定律,获取动力学模型:
(1)
永磁同步直线电机的推力公式为:
F=KfIq
(2)
式中:Kf为永磁同步电机的推力公式,Iq为电机电流。
考虑位置环带宽远低于电流环带宽,可将电流Iq与电压Uq考虑为线性关系:
Iq(s)=0.75Uq
(3)
通过拉普拉斯变换,电压U到位移X的传递函数为:
(4)
采用正弦扫频信号进行系统辩识,获取(4)式系数:
b1=3782;a1=8.44;a2=7.12e-6
(5)
相比于参数辨识后的系数,a2项系数基本为0,为方便后续内模PID的设计,a2项系数忽略不计,将根据系统辨识获取的参数得到辨识模型:
(6)
根据系统辩识获取的传递函数方程,通过DFT分析获取系统开环bode图,如图3所示,系统模型在低频拟合是准确的,高于100 Hz的频率下模型拟合较差。
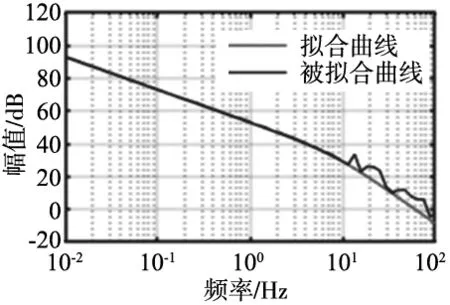
图3 运动平台开环频率响应
2 内模PID控制器参数设计
内模型控制器(IMC)假设一个与物理模型相同的理想模型,将理想模型与物理模型进行相互抵消,实现等同于参考输入的曲线输出,系统框图如图4所示。
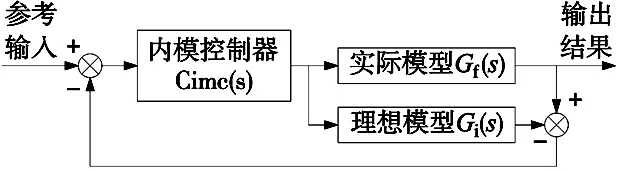
图4 内模控制器系统框图
根据已有的二阶模型,构造滤波器:
(7)
式中:λ为滤波系数,构造滤波器设计PID参数:
(8)
综上所述,根据系统辩识的传递函数,在频率为100 Hz以内的系统拟合程度较高,选取滤波系数为100 Hz,因此,PID系数可确定为:
kp=3.090 4;ki=22.316 2;kd=0.052 9
(9)
3 基于强化学习的内模滤波系数在线优化
内模PID控制器参数调节参数简单,只需调节滤波系数,即可获取PID三个控制参数,实现平台精密运动控制,但是需要辩识的模型足够精确,采用单一的传递函数模型难以涵盖实际物理特性,强化学习作为一种数据驱动控制算法,与环境进行交互累计经验,一定程度上降低对模型的依赖,为了提高数据利用效率和考虑模型误差,本文将采用概率推理学习架构(probabilistic inference for learning control,PILCO)作为强化学习控制算法。
PILCO算法属于将整体架构分为3层。底层利用高斯过程进行数据拟合概率动力学,中间层根据已有的概率动力学进行策略评估,评价采取策略的明智性,最后,利用随机梯度算法进行策略优化,不断根据策略评估修正后续策略,图5为PILCO算法架构图。
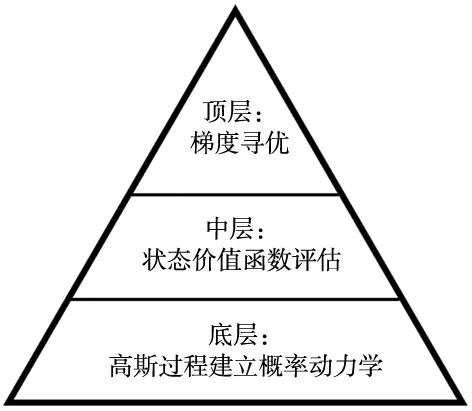
图5 PILCO算法结构图
3.1 概率动力学建模
根据马尔可夫决策过程的定义,当前时刻t的状态与上一时刻t-1的状态和动作相关,其关系表达为:
xt=f(xt-1,ut-1)
(10)
为了考虑模型的不确定性,采用高斯过程建立动力学模型,以状态和输入集合作为数据,即X=[(x1,u1),(x2,u2),(x3,u3),…,(xn,un)],标签值为Y=[y1,y2,…,yn],标签值与数据的关系为:
yt=xt-xt-1+ξt
(11)
式中:xt∈X,yt∈Y,ξt为高斯噪声,为了在t-1时刻的状态下预测t时刻,满足如下高斯分布公式:
(12)
利用平方指数协方差作为内核函数:
(13)
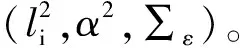
(14)
式中:y*为预测值,k*=k(X,x*),k**=k(x*,x*)。
3.2 策略评估
假设在策略π下的期望回报Vπ,初始状态P(x0)满足高斯分布,为强化学习的期望回报可表示为:
(15)
式中:c(x)为惩罚函数,惩罚函数采用马氏距离;w为加权系数,σc为缩放系数,惩罚函数表达式如下:
(16)
因此,获取状态分布p(xt)即可获取得到当前状态价值,可用于后续策略优化,状态分布p(xt)的推导较为复杂,可参考文献[12]关于通过高斯过程建立强化学习论文的推导,基本流程如图6所示。

图6 PILCO推导流程图
根据上述流程,得到p(xt)的期望和方差:
(17)
3.3 策略优化
基于上述推导的p(xt)和构造的惩罚函数c(xt),可得到状态价值函数Vπ,为了使策略达到最优,需要最小化价值函数Vπ:
π*∈argminVπ(x0)
(18)
利用共轭梯度法对状态价值函数Vπ求梯度,获取均值和方差梯度表达式:
(19)
3.4 内模控制在精密运动平台的PILCO策略应用
前面介绍了PILCO的基本原理,若直接以PILCO作为控制器,根据当前状态变量直接输出对平台输出电压值,不仅收敛差,而且输出电压值不连续,容易造成平台的损坏,因此,需要通过传统控制算法提前保证平台的收敛性,利用PILCO优化内模控制器的滤波系数λ。
本文利用以输出误差e作为状态观测量,滤波系数λ作为动作输出,惩罚函数采用式(16)的c(x),构建强化学习智能体。控制系数框图如图7所示。
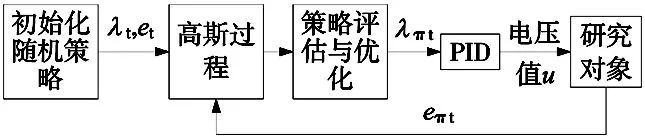
图7 IMC-PILCO工作流程图
首先需要定义初始化滤波系数λ的范围,为了提高强化学习在动作范围取值的稳定性,提前设置初始滤波系数λ0,设置滤波系数变化范围Δλ,激励函数采取在滤波变化范围Δλ下随机采样,h,i为自定义设置范围的上下限,滤波系数λ可通过下式计算:
λ=λ0+Δλ,Δλ∈(h,i)
(20)
将滤波系数λ代入式(8)中的PID系数,从而获取Kp,Ki,Kd数值大小,根据PID计算公式输出相应电压值,本文采取的参考曲线为行程10 mm,速度0.06 m/s,加速度1g的梯形曲线,将研究对象的位移值与参考曲线做差获得误差e,误差e的差分为Δe。
通过将(e,Δλ)作为输入数据,Δe作为输出标签,构建数据集采用高斯过程拟合概率动力学模型,通过共轭梯度最小化状态价值函数,根据式(20)在不同误差状态下自适应输出最优的滤波系数λπ,再将最优滤波系数λπ得到PID参数,将PID参数得到的电压输入到研究对象得到跟随误差,以(eπ,Δλ)和Δe构建数据集代入式(10)~式(12)进行迭代,直至满足需求。
4 运动平台的实验验证
为了验证算法的有效性,将PILCO内模优化算法应用到实际精密运动平台,运动平台放置于隔振基座上,Dspace控制器与直线光栅和直线电机驱动器进行连接,分别获取平台的实时数据和实时驱动直线电机,上位机将算法发送至Dspace控制器,Dspace控制器将算法的控制电压输入至直线电机驱动器进行智能闭环控制,平台实际结构图8所示。

图8 平台实际结构示意图
Dspace将连续传递函数自动转化为离散传递函数,因此,从式(8)可知,当λ越小,PID三个系数越大,容易造成系统的不稳定,因此,需要选择合适的内模滤波系数,根据第3节得到的辨识模型和内模PID参数,依据bode图选取初始滤波系数为λ0=0.01,定义PILCO的动作范围为Δλ=[-0.005,0.005],因此,可通过在此范围内随机采样得到动作序列{Δλ1,Δλ2,Δλ3,…,Δλn},根据式(8)和式(20)代入PID参数从而得到电压值{u1,u2,u3,…,un},将电压值输入至运动平台,输入集和输出集分别为:
(21)
根据已有的硬件系统,离散时间设置为334 Hz,采样频率为1 s,即初始数据集内含有334对输入输出对,经过4次迭代后,控制误差基本收敛,如图9所示。
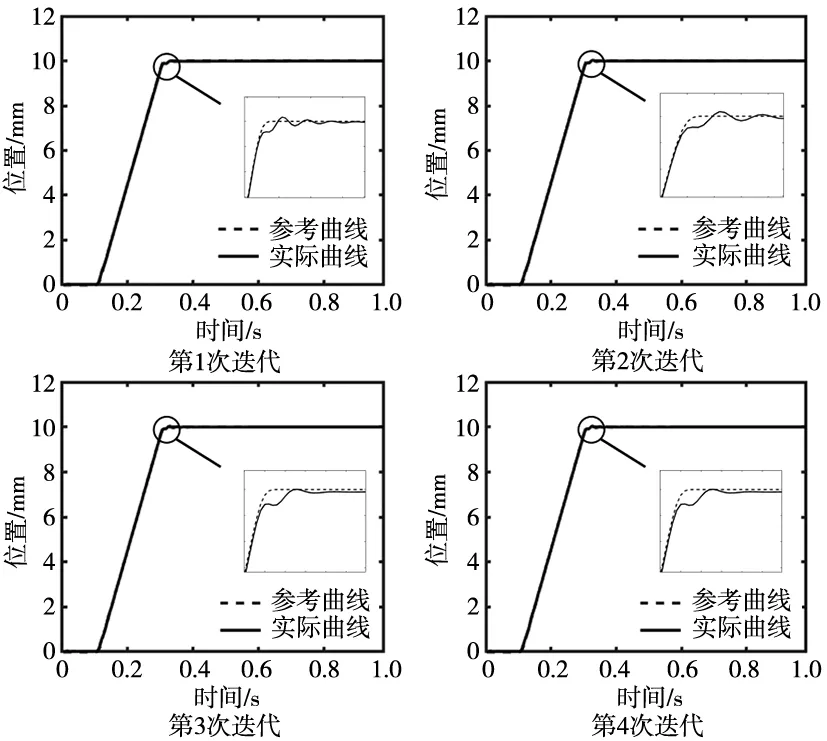
图9 迭代控制效果图
将第4代的控制效果与使用滤波系数λ=0.01的内模控制器作比较,可得到经过PILCO优化后的内模PID控制器最大跟随误差减少了78.372%,误差对比图如图10所示。
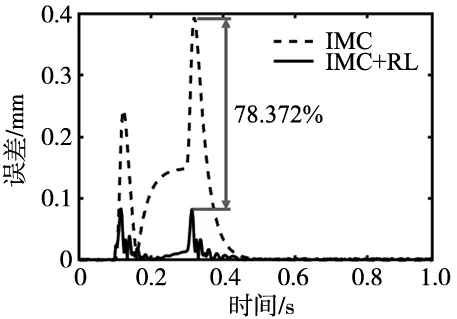
图10 梯型曲线跟随误差比较图
为了验证所提算法的泛化性,以第4次训练后的强化学习智能体作为内模控制器的优化方法,设置参考输入为正弦信号,正弦信号位移曲线R、速度曲线V如式(12)所示,正弦曲线的速度随时间不断变化。
(22)
设置离散时间为334 Hz,采样频率为1 s,通过实验获得参考输入输出曲线如图11所示。
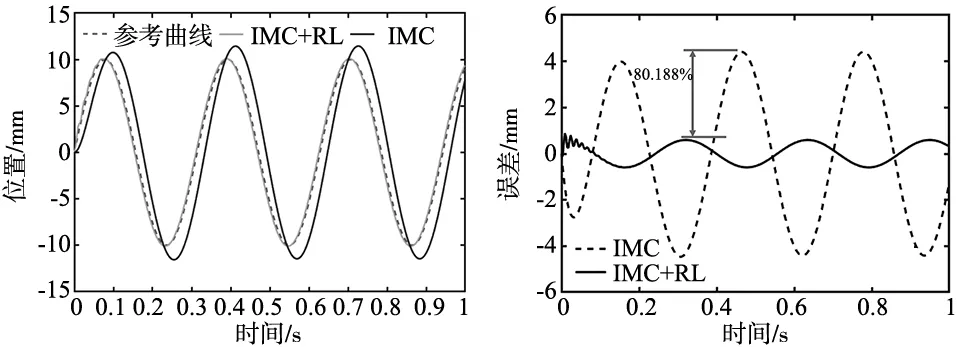
图11 正弦曲线位移输出图 图12 正弦曲线跟随误差比较图
与未优化的内模控制器效果相比,通过PILCO优化后的内模控制器明显降低跟随误差,最大跟随误差降低了80.188%,正弦曲线跟随误差对比如图12所示。
综合实验数据的比较结果,如表1和表2所示,在梯型曲线控制效果上,经过PILCO优化后的控制器在定位过程超调量与平均跟随误差分别降低了78.372%和86.667%,在正弦曲线的控制效果上,经过PILCO优化后的控制器在最大跟随误差与平均跟随误差分别降低了80.188%和85.950%,因此,对于跟踪指标要求较高的场合,本文所提算法具有一定的先进性。
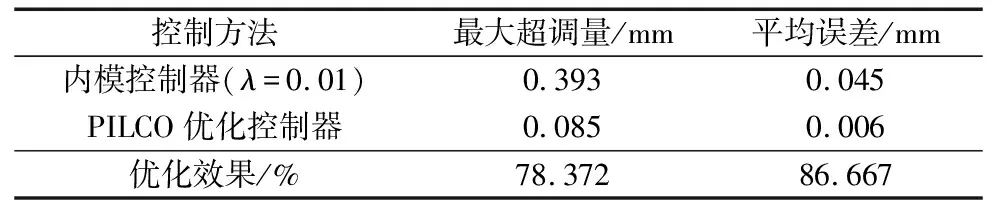
表1 梯型曲线控制效果比较

表2 正弦曲线控制效果比较
5 结论
(1)提出了一种基于概率推理学习控制(PILCO)架构的内模控制器优化方法,以内模控制保证强化学习优化的收敛性,利用PILCO的高斯过程建立概率动力学和数据交互补偿内模控制器建模不精确的误差,从而达到自适应调节滤波系数的目的,实现内模控制器与强化学习的高效结合。
(2)以精密运动平台为研究对象,与未优化的内模控制器(IMC)相比,在梯形曲线的控制效果上,本文所提方法在跟随误差上显著降低,定位过程最大超调量降低了78.372%,平均误差降低了86.667%,在正弦曲线的控制效果上,最大跟随误差降低了80.188%,平均跟随误差降低了85.950%,实验验证了所提优化方法的有效性。
综上所述,本文将PILCO算法框架与内模控制器进行结合,基于PILCO算法在线优化内模滤波参数,具有良好的先进性,可广泛应用于自适应精密运动控制领域。

