基于缩减基法的刚柔耦合运动平台快速优化*

黄观新,卢永和,张 驰,杨志军

(广东工业大学省部共建精密电子制造技术装备国家重点实验室,广州 510006)

0 引言

半导体产业中的精密定位需求越来越急迫,对定位精度的要求也越来越高[1]。刚柔耦合运动平台利用柔性铰链的弹性变形补偿摩擦死区,实现了纳米级定位[2-4]。力学分析对提高刚柔耦合运动平台的定位精度等级重要性不言而喻[5]。精密定位平台的结构复杂,设计参数较多,采用有限元方法分析时,每一次修改设计参数后都需要重新建立模型,由于分析模型的空间维度较大,完成一次分析耗时较久。结构优化时需要不断改变设计参数并求解平衡方程,因此会严重影响优化效率,计算效率的提高是实行高效优化的必要条件[6-8]。

遗传算法是一种通过模拟生物界的遗传和变异而形成的全局优化概率搜索方法,能有效避免收敛于局部最优解,目前该算法广泛应用于工程问题的结构优化中[9-11]。但其每迭代一次都需要计算n个力学平衡方程(n指优化计算次数),遗传算法优化耗时较长的缺陷限制其被广泛应用。在工程实际中遗传算法往往结合近似模型使用,通常使用神经网络来建立近似模型[12-14]。神经网络适合求解复杂问题的最优解,是一种有效的优化设计方法[15]。但使用该方法需要建立复杂的训练模型,同时样本数据对预测的结果影响很大,样本数据不充分时计算结果误差较大,此外神经网络不适用于要求计算精度较高的问题[16]。

缩减基法(reduced basis method)是一种求解近似模型的分析方法,目前RBM对于非线性问题的求解以及误差分析有较为成熟的理论成果[17-18]。其中在汽车、模具等领域的结构优化方面应用广泛[19-22],在瞬态分析、热传导分析等领域的技术研究也十分成熟[23],然而RBM在高精密定位平台的机构分析中应用甚少。

本文针对刚柔耦合平台的受力特点对缩减基法进行扩展,提出一种基于多工况RBM的刚柔耦合运动平台结构快速优化方法,首先构造低维空间的样本参数,其次利用样本参数的线性组合求解新的位移向量,并对多工况RBM和有限元方法计算的位移结果进行误差分析。遗传算法在不断迭代过程中,直接使用RBM的计算结果进行全局搜索寻求目标值,以此实现快速优化。

1 刚柔耦合运动平台结构与原理

1.1 刚柔耦合运动平台的结构设计

刚柔耦合运动平台由刚性框架和工作平台组成,几何模型如图1所示。其中刚性框架固定在滑块上,用于运动方向导向。直线电机的动子与柔性工作平台底部连接,用于施加驱动载荷。柔性铰链一端固定于刚性框架,另一端连接工作平台,并沿着导轨移动。柔性铰链组的几何模型如图2所示。柔性铰链分为两种:一体式柔性铰链与工作平台一体加工,用于消除装配误差,实现高精度定位;弹片式柔性铰链用于调节工作平台的刚度,起缓冲作用。

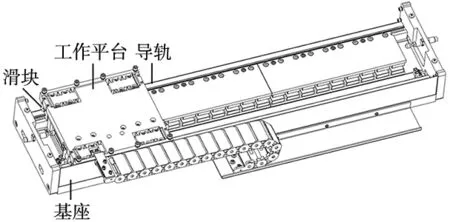
图1 刚柔耦合运动平台几何模型

图2 柔性铰链几何模型

1.2 刚柔耦合运动平台的工作原理

通过驱动直线电机带动柔性工作平台运动,当驱动力克服导轨的摩擦力时,工作平台实现长行程运动。当驱动力小于框架与导轨之间的最大静摩擦力时,刚性框架处于静止状态,此时工作平台借助柔性铰链的弹性变形补偿摩擦死区。相比于传统精密运动平台,刚柔耦合运动定位平台将导轨与工作平台间的摩擦力转化为柔性铰链的弹性力,利用柔性铰链的弹性变形补偿位置误差,实现更高精度定位。

2 缩减基法基本原理

结构优化是刚柔耦合定位平台实现高精度定位的关键技术手段,因此首先需要构造有限元方程。设刚柔耦合定位平台的系统平衡方程为:

K(μ)d(μ)=f

(1)

式中:μ指设计参数,是r维向量;K(μ)为h×h的总体刚度矩阵,d(μ)为节点位移向量,f为载荷向量。

在优化过程中,设计变量的值发生改变时导致需要重复求解上式方程。由于维数h很大,每次需要花费大量时间求解,导致优化设计受到限制。为了避免求解有限元方程时耗费大量时间,有必要采用高精度高效率的缩减基法求解位移。

RBM的求解步骤为,首先在设计参数可行域内,选取N组值作为样本参数组成样本空间TN={μ1,μ2,…,μN},μn表示第n组样本参数(n=1～N,用于表示样本组的下标,其意义在本文中保持不变),通过式(1)求解出对应的位移向量d(μn),将N组位移解组成缩减基矩阵R。

R={d(μ1),d(μ2),…,d(μN)}

(2)

假设真实h维空间中的位移解可以用缩减基矩阵中位移向量d(μn)的线性组合来表达,并且d(μn)线性无关。则在选取新的设计参数时,位移解可表达为:

d(μ)=Rγ(μ)

(3)

式中:γ(μ)为系数向量。

系统能量为:

(4)

将式(3)代入式(4)得到系统的能量为:

(5)

根据能量最小的原则,由式(5)可得:

RTK(μ)Rγ(μ)=RTf

(6)

令KN(μ)=RTK(μ)R,fN=RTf,式(6)可简化为:

KN(μ)γ(μ)=fN

(7)

求解式(7)可得γ(μ),将其代入式(3)即可得到新设计参数对应的位移向量d(μ)。

式(7)中KN(μ)为N×N的矩阵,选取新的设计参数时,由于h远远大于N,采用缩减基法可将求解h阶系统平衡方程(1)转化为求解N阶方程(7),减少了大量计算。对于设计变量在刚度矩阵中可分离的情况,计算量可进一步减少。假设刚度矩阵可分离为:

(8)

式中:φj(μ)为设计变量μ的标量函数,Kj为与设计参数无关的刚度矩阵,则缩减刚度矩阵KN(μ)可表达为:

(9)

(10)

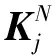
3 刚柔耦合运动平台的快速优化

3.1 建立优化模型

本文以刚柔耦合运动平台的简化模型作为优化结构建立数学模型,在此基础上优化尺寸参数。针对柔性铰链的小变形采用以下假设:柔性铰链发生的弯曲变形均为弹性变形;本构方程满足虎克定律。刚柔耦合运动平台简化模型的参数设置如表1所示。

表1 刚柔耦合运动平台简化模型的参数设置

(1)设计变量。柔性铰链几何模型如图2所示,前期实验研究显示,柔性铰链的厚度t1,t2对刚柔耦合运动平台的性能有显著影响,因此选取柔性铰链厚度为设计变量,即:

μ=[t1t2]

(11)

刚柔耦合运动平台各方面的性能涉及多种静力学工况,其控制方程为:

K(μ)D(μ)=F

(12)

式中:D(μ)和F分别为多工况的位移矩阵和载荷矩阵。

(2)目标函数。刚柔耦合运动平台的驱动器位于工作台下方,工作台受到驱动力时沿着导轨方向运动。但由于载荷偏心,工作台需要承受额外的扭转力矩,因此需要设计更高的扭转刚度来抵抗因扭转力矩产生的扭转位移θx,表达式为:

(13)

式中:d(θ,x)为绕x轴扭转的位移向量,a为θx在d(θ,x)中的下标,F(θ,x)为工作平台中心点o处沿y方向的集中力fy和绕x轴的转矩wx组装得到的载荷向量。

优化时寻找最佳的t1,t2,使得平台的最大扭转位移达到最小,故目标函数可以表示为θx,max。

(3)约束条件。柔性铰链在高速高频运动状态下存在应力集中的问题会导致疲劳破坏,所以柔性铰链的厚度需要在一定的范围内选取。柔性铰链的补偿能力决定了刚柔耦合运动定位平台的精度等级,因此需要设计合适尺寸参数的柔性铰链。为保证合理设计刚柔耦合运动平台,要求工作平台具有一定的工作刚度Kv以及承载刚度Kf,分别用式(14)、式(15)表达为:

(14)

(15)

式中:Fy、Fz分别为o点处沿y轴的集中力fy和沿z轴的集中力fz组装得到的载荷向量,uy、uz分别为工作方向和承载方向的位移,b为uy在dy中的下标,c为uz在dz中的下标。

工作刚度和承载刚度的许用范围可估计如下:根据前期实验数据,平台在工作时的载重力约G为100 N,刚性框架与导轨间的摩擦系数α约为0.5,摩擦力可表达为:

f=αG

(16)

根据平台定位精度的标准,要求柔性铰链补偿的位移需要大于1 μm,同时承载方向的位移需要小于0.02 μm。以此为基础,可计算出Kv和Kf的极限值,具体数值如表2所示。另外,柔性铰链厚度的取值范围也列于表2中。

表2 平台设计参数取值范围

综合上述分析,工作平台的优化问题可以概括为,在柔性铰链的厚度取值范围内并且工作平台刚度满足要求的前提下,选择最合适的柔性铰链厚度,使得工作平台的最大扭转位移达到最小。优化问题可用以下数学模型表达:

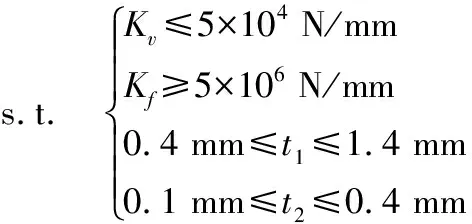
(17)

3.2 优化模型求解

3.2.1 优化算法

本文使用遗传算法求解式(17)优化问题,具体流程为:

(1)使用二进制编码染色体。

(2)计算机随机选取15个个体组成初始种群,并计算每个个体的适应值。

(3)使用单点交叉的方式选择父代交叉。

(4)当函数容差小于10-3时,刚柔耦合运动平台的目标函数收敛。

优化过程如图3所示,优化算法所使用的参数设置如表3所示。

表3 优化参数设置

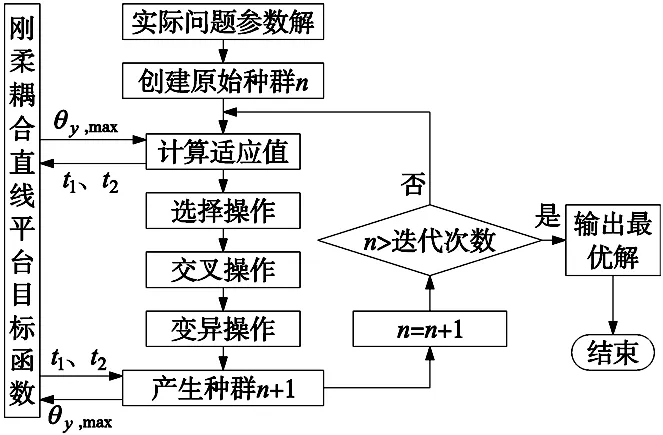
图3 遗传算法流程框图

3.2.2 正问题计算

优化问题式(17)需要考虑刚柔耦合运动平台的3个工况Fl(l=y,z,θx,用于表示不同工况的下标,其意义在本文中保持不变),因此式(12)中的D(μ)和F可分别记为:

(18)

再计入柔性铰链与刚性框架以及工作平台间的连接约束方程C×D(μ)=0,采用拉格朗日乘子法的形式可将刚柔耦合运动平台的平衡方程表达为:

(19)

式中:Λ为拉格朗日乘子矩阵。

优化过程中需要反复求解式(19),因此,本文提出多工况缩减基法对其进行快速求解。多工况缩减基法的计算过程可分为离线阶段和在线阶段:

(1)离线阶段:

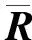
(20)

则式(19)的解可假设为:

(21)

式中:Γ为N×3的系数矩阵。

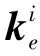
(22)

(23)

式中:t为柔性铰链的厚度,Bk(k=m,b,s)和Dk(k=m,b,s)分别为对应的应变矩阵和本构矩阵,Ai为单元面域。考虑到一体式柔性铰链和弹片式柔性铰链的厚度与材料不同,可将式(22)进一步整理为:

(24)

式中:Q1和Q2分别为一体式柔性铰链和弹片式柔性铰链的单元集合,且:

(25)

记

(26)

(27)

则式(19)变为:

(28)

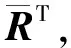
(29)

式中:

(30)

(31)

(32)

(2)在线阶段:

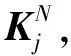
②对于每一个μ*,求解缩减式(29),得到系数矩阵Γ(μ*)。

③将系数矩阵Γ(μ*)代入式(21)即可得到多工况的位移矩阵。

3.2.3 误差分析

样本参数的选取直接影响缩减基算法的计算精度,为了反应出设计参数整体特性,本研究使用拉丁超立方抽样法采样。确定样本区间t1∈[0.4,1.4],t2∈[0.1,0.4],将厚度区间分成8份,分层随机抽取一个数值,并求解8组厚度的平衡方程得到位移向量,然后将位移向量组成样本空间。

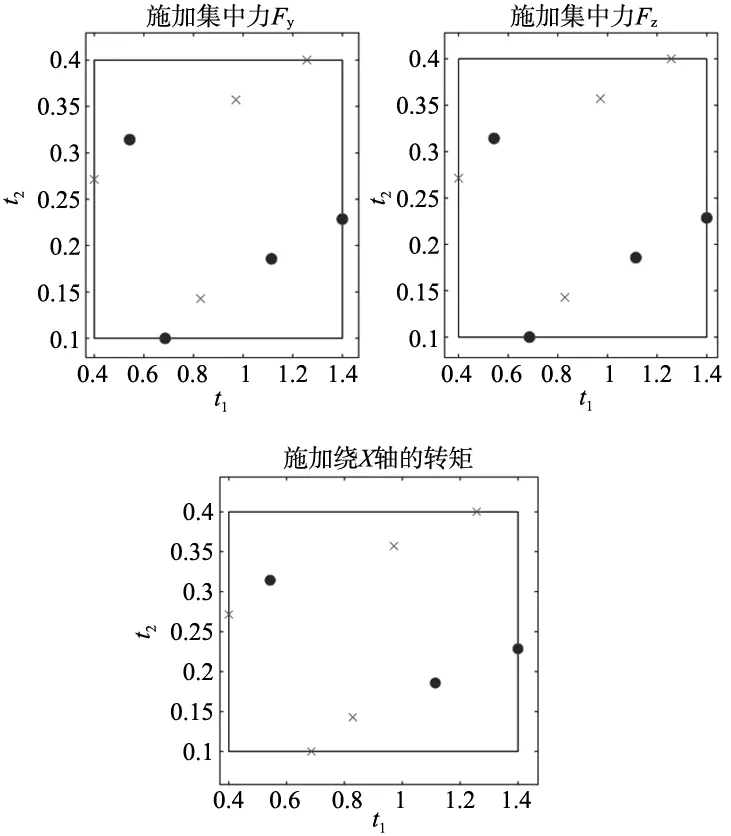
图4 样本数据

将有限元方法与RBM的计算结果作误差分析以验证RBM的计算精度,在μ的可行域内随机选择5组设计参数进行测试,如表4所示。

表4 设计参数取值

使用有限元方法和缩减基法分别计算系统位移向量,采用两种方法计算的相对误差可表达为:

(33)

为了验证缩减基法在刚柔耦合运动平台上应用的可靠性,本文针对以下3种工况做误差分析:以工作平台中心点o作为输出点,分别计算在工作方向的平动位移uy,承载方向的平动位移uz,绕X轴的转动位移θx。根据表4的设计参数,利用式(33)可计算出相对误差εd,y方向、z方向和θx方向的误差结果如表5所示。

表5 相对误差εd

根据表5的数据可知,RBM计算θx的最大误差为8.356×10-6,沿y方向平动位移的最大误差为1.475×10-13,沿z方向平动位移的最大误差为5.522×10-9。证明RBM具有良好的计算精度,适用于刚柔耦合运动平台的分析中。

使用遗传算法做优化设计研究需要更改设计参数时,直接调用RBM的计算结果。优化时RBM重复计算在线阶段的步骤即可。优化计算参数如表6所示,优化结果如表7所示。

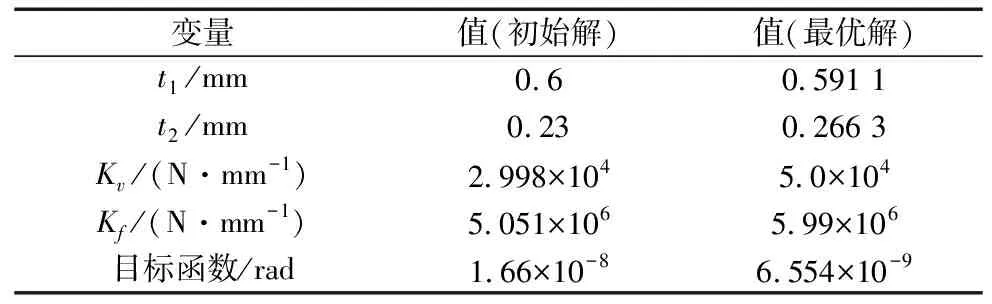
表7 遗传算法优化结果

由表6可以看出,使用有限元法计算一次系统平衡方程需要85 s,而RBM仅需0.001 7 s,其耗时远远小于有限元方程,应用RBM代替有限元法可节省约3.512×106s。迭代次数与最优解的关系如图5所示。从图5可知,计算到第26代时目标函数搜索到最优解6.554×10-9,此时t1为0.591 1 mm,t2为0.266 3 mm。

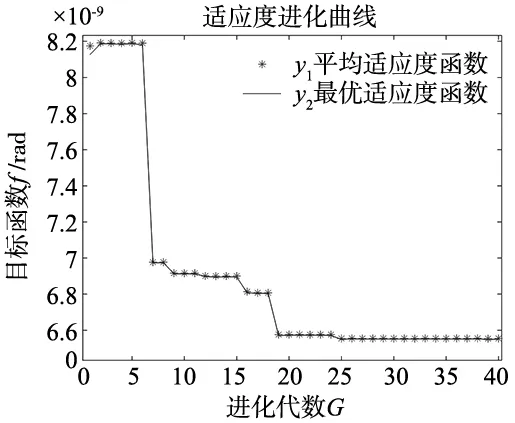
图5 迭代次数与最优解关系图

根据表7数据,使用有限元软件ABAQUS对柔性铰链的初始值和最优值的位移结果进行对比验证,初始值的位移结果如图6所示,最优值的位移结果如图7所示。验证结果表明,刚柔耦合运动定位平台的最大扭转位移减少了17.2%。

图6 初始值位移云图

图7 最优值位移云图

4 结论

本文将RBM的应用扩展到多工况领域,并结合遗传算法对多工况的刚柔耦合运动平台进行结构优化。对比RBM和有限元法的优化结果得到:使用两种方法计算的结果十分相近,最大的计算误差仅有8.356×10-6,证明RBM应用在多工况领域具有良好的精确度;RBM完成优化计算的时间远远低于有限元法,优化时间可节省3.512×106s,表明RBM具有高效的优化效率。对比优化前后的目标函数值发现平台的扭转位移减少了17.2%,平台的工作性能得到提升,因此可为高速精密定位平台的结构设计和精度保持研究提供参考。