基于扩展角度控制的改进RRT机械臂路径规划*

朱 花,郝 赫,阳 明,刘正超

(江西理工大学机电工程学院,赣州 341000)

0 引言

随着工业自动化水平的不断提升,越来越多的机械臂被应用到工业生产领域,以代替人类完成一些高精度或特殊环境下的工作任务,有效提升了生产效率[1]。路径规划技术是机械臂的研究热点和难点之一[2-6],其任务是使机械臂自主地规划出一条从起始位置到目标位置,且能避开所有障碍物的路径[7]。路径规划的成功率以及路径质量的高低是影响机械臂能否完成任务的关键因素[8]。

机械臂的路径规划算法主要有Dijkstra算法[9]、A*算法[10]、PRM算法[11]和RRT算法等[12]。基于采样路径的RRT算法具有结构简单,搜索能力强,且能适应高维空间的优点,被广泛应用到机械臂的路径规划中[13]。但是RRT算法也存在着缺乏导向性、节点数量多、扩展方向随机性强且路径不是最优等问题[14]。目前,国内外大量学者针对RRT算法的不足提出了改进方案。钟华庚等[15]采用重选父节点和区域排斥策略剔除无效节点,缩短迭代时间;JEONG等[16]提出一种Quick-RRT*算法,将父节点点集扩大到预设的范围内,减小路径成本;LAVALLE等[17]提出一种Bi-RRT算法,分别从起点和终点生成两棵随机树,加快收敛速度;张勤等[18]通过柯西分布的方法进行启发式采样,引入节点拒绝策略,提高局部搜索速度;韩康等[19]提出一种Obi-RRT算法,采用智能采样,拒绝高成本路径点,降低算法的路径成本;崔永杰等[20]引入评价指数,实时引导随机树的扩展。

上述文献提及算法主要对搜索速度、采样方式和路径质量进行了优化,但是没有对新节点的扩展方式进行改进。本文主要针对RRT算法新节点扩展方向随机性强的问题,提出一种改进RRT算法,首先引入概率目标偏置函数,使新节点以一定概率朝向目标点生长;然后提出扩展角的概念,并通过障碍占空比约束扩展角的大小,使算法增加导向性的同时保留一定的随机性,提高算法的成功率;随后对生成的路径进行优化,增加机械臂运动时的平稳性;最后通过MATLAB平台对本文算法进行仿真,验证算法的有效性和可行性。

1 RRT算法介绍

RRT算法是一种基于随机采样的全局路径规划算法,其原理如下:①首先确定路径的起始点xstart和目标点xgoal,以起始点xstart作为根节点开始构建树;②在规划空间内随机采样生成随机点xrand;③遍历树,找到树中距离随机点最近的节点,记为最近点xnear,并以随机点xrand方向扩展一个步长的距离,得到新节点xnew;④若新节点与最近点的连线存在障碍物,则舍弃新节点,重新开始采样;若连线无障碍物,则将新节点添加到树中;⑤重复上述步骤,直到新节点与目标点之间的距离小于给定的目标点阈值,则连接目标点与新节点,成功生成路径,规划结束。扩展原理如图1所示。

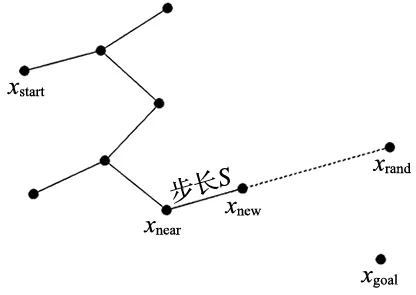
图1 RRT算法扩展原理

新节点生成公式为:

(1)

2 改进RRT路径规划算法

本文提出的改进RRT算法首先使用概率目标偏置函数,使采样点以一定概率偏向目标点,随后计算扩展角和障碍占空比的大小,通过障碍占空比约束扩展角的大小,生成新采样点。随后生成新节点,并判断新节点与最近点连线上是否有障碍物。算法整个流程如图2所示。

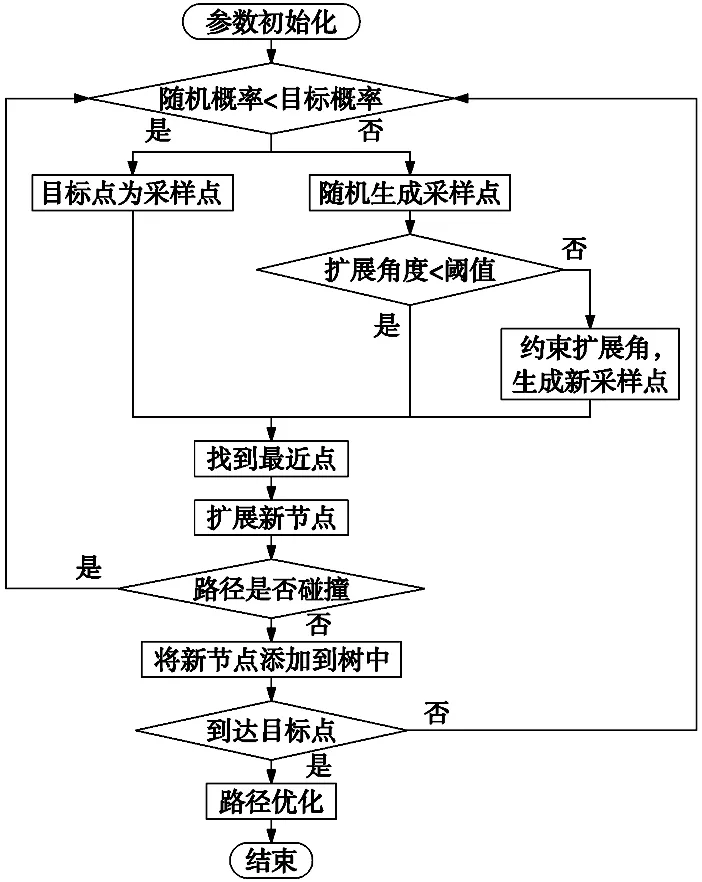
图2 改进RRT算法流程图

2.1 概率目标偏置函数

根据路径规划空间中障碍物的分布情况设置目标概率a(a∈[0,1]),当路径规划空间中障碍物较多时,a取较小值,反之a取较大值。在区间0～1内随机生成一个概率p,当随机概率pa时,采样点仍为随机点。随机点公式为:

(2)

式中:Randomsample(x)为随机采样函数。

2.2 新节点扩展角度约束

首先引入扩展角θ的概念。当采样点的采样方式为随机采样时,分别求得最近点xnear与随机点xrand,最近点xnear和目标点xgoal的方向向量,将两向量的夹角定义为扩展角,如图3所示。

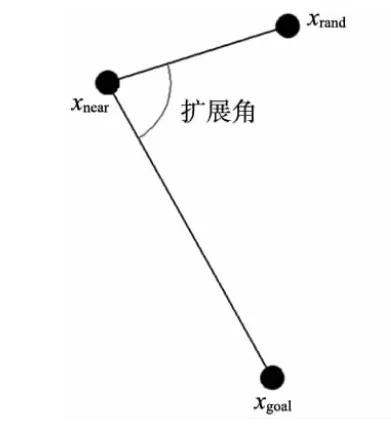
图3 扩展角示意图

扩展角θ的计算公式为:

(3)

扩展角的大小反映了新节点的扩展方向。扩展角越大,说明新节点的扩展方向离目标点越远,导致算法的规划效率变低。所以需要控制扩展角的大小,具体的做法为:设置扩展角阈值为α,扩展角阈值的大小根据路径规划空间中障碍的分布情况决定,当障碍物较多时,α取较大值;当障碍物较少时,α取较小值。算法进行一次随机采样后,计算扩展角的大小θ,并判断扩展角的大小是否在扩展角阈值内。当扩展角小于阈值α时,不对扩展角进行处理;当扩展角大于阈值α时,通过式(4)生成新的扩展角θ1:

(4)

式中:k为障碍占空比,其值为二维空间下以最近点为圆心,两个步长为半径画圆,圆内障碍物与圆面积的比值;三维空间下以最近点为球心,两个步长为半径画球体,球内障碍物与球体积的比值。

为求出障碍占空比k,需先求得二维空间下障碍物的面积,三维空间下障碍物的体积。在二维空间中,为便于计算,取障碍物边界函数为障碍物与检测圆两交点的一次函数。障碍物的面积Sobstacle计算公式为:

(5)

式中:x1、x2为检测圆与障碍物的交点,d为最近点与x1x2连线的距离,s为步长。

在三维空间中,为便于计算,将障碍物简化为球形。则障碍物的体积Vobstacle计算公式为:

(6)

式中:h1、h2为球缺的高,r1为障碍物半径,r2为检测球半径。

由此可求得障碍占空比k的表达式为:

(7)

式中:R为采样空间维度。

k值的大小反映了最近点附近的障碍物分布情况。k值较大时,说明最近点附近的障碍较多,此时适当降低对扩展角的约束以获得较大的扩展角,以此来增强算法的探索性,避免算法陷入局部最优。当k值较小时,说明最近点附近障碍物较少,故增大对扩展角的限制,使扩展角变小,增加算法的收敛性,使算法更快收敛到目标点。扩展角被约束后,随机点位置也随之变化,整个过程如图4所示。

新扩展角生成后,新采样点生成公式为:

(8)

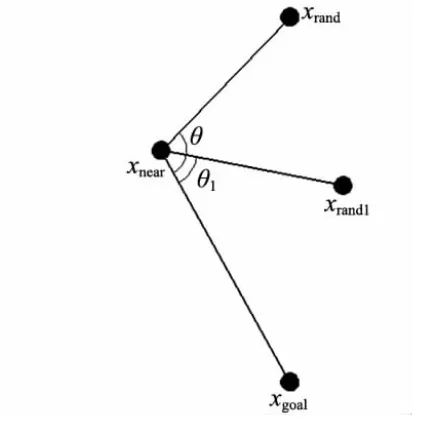
图4 扩展角约束示意图

以新扩展角生成的新节点生成公式为:

(9)

故新节点生成公式为:

(10)

式中:s为步长,θ为扩展角,α为扩展角阈值。

扩展角阈值过大,会导致算法的规划效率变低,导致优化效果不明显;扩展角阈值过小,则会使路径陷入局部最优,导致规划失败。所以要根据当前环境合理选择扩展角阈值的大小,以提高算法的稳定性。

2.3 路径剪枝优化

通过前文所述的改进方法可以大大缩短RRT算法的规划时间,但是由于RRT算法的随机性,其规划出的路径仍含有冗余节点,这不仅会增加路径成本,还会导致机械臂在实际运行中的平稳性降低。本文使用剪枝优化删去冗余节点,算法流程和优化过程如图5和图6所示。

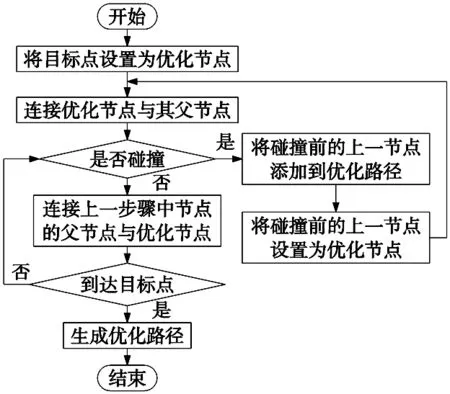
图5 剪枝优化流程图

图6中,原始路径为起点—5—4—3—2—1—终点,剪枝优化后的路线为起点—3—2—终点。通过对比发现,剪枝优化后的路径节点更少,路径长度也大大缩短。

2.4 路径平滑优化

通过剪枝优化可以去除路径中的冗余节点,但路径中仍然存在一部分必要节点。由于这些节点的存在使路径发生转折,导致机械臂在实际运行中末端通过转折点时,机械臂关节角会产生突变,不仅会降低机械臂运行的平稳性,还会降低电机的寿命。因此需要对路径进行平滑处理,使其满足路径要求。

本文采用二阶贝塞尔曲线对路径转折点处进行曲线拟合,其公式为:

B(t)=(1-t)2P0+2t(1-t)P1+t2P2

(11)

式中:t为比例系数,P0、P2为数据点坐标,P1为控制点坐标,B(t)为拟合后的曲线坐标。

取要优化的节点为P1,为了防止拟合后的曲线碰到障碍物,将转折点P1前后路径方向距离1/2步长处分别设置为数据点P0、P2。拟合过程如图7所示。

图7 曲线拟合示意图

图7中,黑色线段为原路径,红色线段为拟合后的路径。对比发现,拟合后的路径有效祛除了转折点,平滑度大大提升。

3 仿真实验及数据分析

3.1 二维空间仿真实验

为了验证上述改进算法的可行性,将本文算法与普通RRT算法通过MATLAB仿真平台在不同环境下进行对比仿真实验,仿真环境分为普通环境和特殊环境两种,其中普通环境分为简单环境和复杂环境;特殊环境分为狭窄通道环境和迷宫环境,具体环境如图8所示。

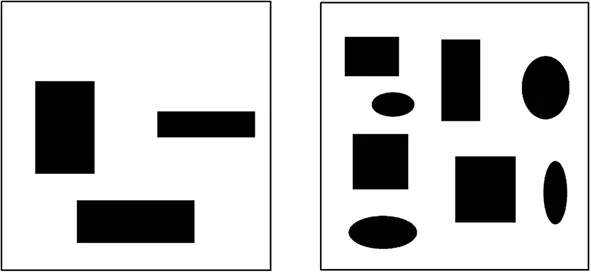
(a) 简单环境 (b) 复杂环境

4种环境地图大小均为[800,800];起始点坐标为(10,10);目标点坐标为(750,750);步长为10;最大迭代次数为5000;扩展角阈值设置为90°。将改进RRT算法与普通RRT算法分别进行50次实验,并收集路径长度、规划时间和成功率,计算出平均路径长度和平均规划时间,通过分析数据以验证改进RRT算法的可行性。

3.1.1 普通环境

由图9和表1可以得出,在障碍物较少的环境下,两种算法均有较高的成功率。相比于普通RRT算法,改进RRT算法规划出的路径有更强的目标导向性,减少了大量的无用路径。由图10和表2可以得出,在障碍物较多的环境下,普通RRT算法的成功率明显下降。相比之下,改进RRT算法具有更好的收敛性和稳定性,规划效率更高。

表1 简单环境仿真数据统计

表2 复杂环境仿真数据统计

(a) 原始RRT (b) 改进RRT

3.1.2 特殊环境

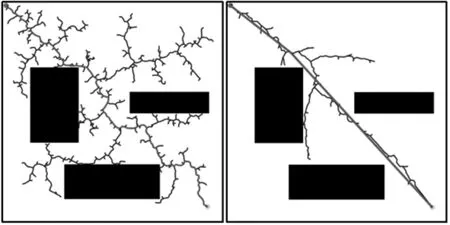
图11主要测试改进RRT算法在狭窄通道下的规划能力。根据图11和表3可以看出,在狭窄通道环境下普通RRT算法的规划成功功率很低,改进RRT算法的成功率可以达到80%的成功率,平均路径长度缩短19.6%,平均规划时间减少52.7%。由此可见,改进RRT算法在狭窄通道环境下有更好的效率和性能。

表3 狭窄通道环境仿真数据统计

(a) 原始RRT (b) 改进RRT

由图12和表4可知,在迷宫环境下改进RRT依然有更短的路径、更少的规划时间和更高的成功率。通过以上仿真实验可以得出,本文提出的改进RRT算法在多种环境下均有良好的稳定性和收敛性,有效的验证了本文算法的可行性。

表4 迷宫环境仿真数据展示

(a) 原始RRT (b) 改进RRT

3.2 三维空间仿真实验

为了验证本文算法在三维环境下的规划能力,使用MATLAB仿真平台对本文算法进行三维仿真实验,设置地图大小为[250,250,250],起始点坐标为(10,10,10),终点坐标为(150,150,150),步长为10,仿真结果如图13所示。

(a) 原始RRT (b) 改进RRT

根据图13可以得出,改进RRT算法在三维环境下可以有效减少无用节点和多余分叉树,且生成的路径更加平滑,验证了本文算法在三维环境下的可行性。

3.3 机械臂避障实验

为了验证本文算法在机械臂实际运行中的可行性,设计一台六自由度机械臂,并使用MATLAB RoboticsToolbox平台进行路径规划仿真实验。实验任务为:使用改进RRT算法规划出一条从起始点到目标点之间可以避开障碍物的路径,并驱动机械臂模型进行实验验证,未碰撞到障碍物即为实验成功。

采用标准DH法建立机械臂数学模型,DH参数如表5所示。

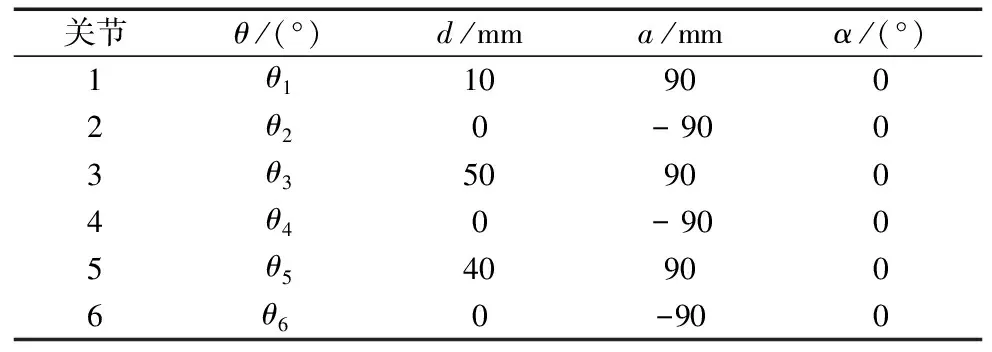
表5 机械臂DH参数表

其中,θ表示连杆角度,d表示连杆偏距,a表示连杆长度,α表示连杆转角。

仿真具体参数设置为:设置起点坐标为(30,-50,0),终点坐标为(30,50,50),步长为5,最大迭代次数为10 000,障碍物简化为实心球体,仿真结果如图14所示。

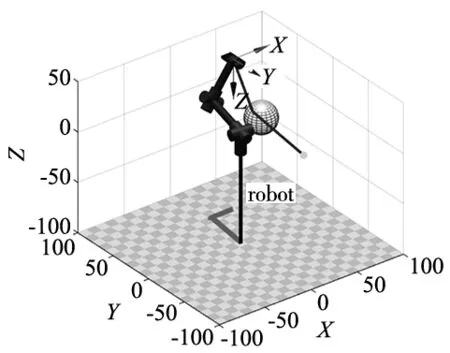
图14 机械臂运行仿真结果

由图14可以看出,机械臂沿着规划好的轨迹从起点运行到了目标点,且成功避开障碍物。验证了算法在机械臂运动中的可行性。

为了验证路径优化策略的可行性,根据原始RRT算法规划出的路径节点和改进RRT算法规划出的路径节点,分别求得机械臂关节角度变化图如图15、图16所示。

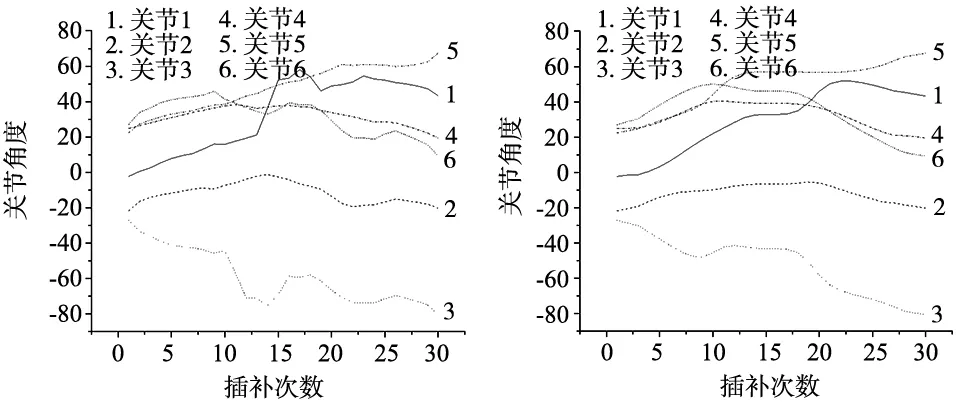
图15 原始RRT关节角度变化图 图16 改进RRT关节角度变化图

通过对比图15、图16可以看出,使用改进RRT算法的机械臂在运动的过程中,关节角度变化更加平稳,没有出现较大的波动,由此可以验证算法路径平滑优化策略的可行性。

4 结束语

本文针对RRT算法存在收敛速度慢、路径冗长且在复杂的环境下成功率低的问题,提出一种改进RRT算法,对原始RRT算法做出以下几点改进:

(1)使用概率目标偏置策略,提升算法的收敛性和规划速度;

(2)使用扩展角度控制策略,限制新节点的扩展方向,有效减少了无用节点的生成;

(3)使用剪枝优化和二阶贝塞尔曲线对生成的路径进行优化,使生成的路径更符合机械臂的运动方式。

通过对比在不同环境下的仿真实验可以得出,改进的RRT算法可以有效提升规划的成功率,且降低了路径长度和规划时间,在不同环境下也有较高的稳定性。