面向菱形双翼布局的超声速有益干扰研究

薛亦菲 曾宏刚 程思野

摘 要： 组合体有益干扰理论利用飞行器各结构组成之间的相互干扰获取增升/减阻等额外的气动收益，常被用于提高飞行器的升阻比，具有较大的应用潜力。以飞行马赫数Ma3的二维菱形双翼为基本模型，利用头部斜激波波后的高压区产生有益气动干扰，分别设计头部斜激波高压区作用于两翼后半部分的减阻方案，以及高压区仅作用于上翼后半部分的增升方案。建立基于激波-膨胀波理论的气动力快速预测方法，针对增升和减阻方案，优化菱形双翼的相对位置及迎角，其中的增升方案能够获得17%的升阻比增量。采用二维流动仿真分析增升方案中产生额外升力的流动机理，进一步分析黏性对激波-膨胀波理论预测结果的影响，有黏模拟预测得到的升阻比相比激波-膨胀波理论预测结果要低29%。有益干扰理论及激波-膨胀波理论能够用于气动布局初步优化，超声速菱形双翼布局可为超声速飞行器提供气动布局优化思路。

关键词：菱形双翼； 气动布局； 激波； 优化； 升阻比

中图分类号：V211.4 文献标识码：A DOI：10.19452/j.issn1007-5453.2023.07.002

超声速飞行中由激波产生的波阻是总阻力的重要组成部分，波阻的大小隨马赫数的增大而增大，超声速飞行器难以获得大升阻比。在超声速飞行器气动特性优化问题中，有益干扰理论[1]是实现飞行器增升、减阻[2]、降噪等气动优化的基础理论之一。

布泽曼双翼[3]（Busemann biplane）设计充分体现出有益干扰理论在超声速飞行器减阻降噪问题中的重要作用[4]。布泽曼双翼采用顶部和底部翼面与流动方向平行的对称气动布局，如图1所示，在理想流动状态下，顶部和底部翼面几乎不会产生激波，能够最大限度消除外部波阻，进而极大地减小飞行阻力，还可用于减弱超声速飞行器的声爆问题。R. M. Licher[5]在布泽曼双翼的基础上叠加一个上翼无厚度的平板双翼，设计出Licher双翼，有效提高了升阻比。刘姝含等[6-7]和华如豪等[8]、马博平等[9]分别围绕布泽曼双翼和Licher双翼进一步开展了气动布局优化研究。

有益干扰理论还能够用于组合体形式的超声速飞行器气动布局设计[10-11]，利用机身与机翼的有益波系干扰，O. Morris[12]设计了低阻的环形翼布局，相似概念的气动布局还有半环形翼布局[13]、伞形翼布局[14]、高压捕获翼布局[15]等。提高升阻比是大多数气动布局优化的目标[16]，设计增升减阻的有益干扰布局方案仍有很大应用前景。

超声速编队飞行技术是另一种利用有益干扰理论获取升力的技术，Y. Goto等[17-18]利用各飞行器之间的气动干扰，设计了一系列适合超声速飞行器的编队飞行方案。M. Rütten等[19]和R. Nangia等[20]的分析表明，超声速斜翼飞行器的近距离编队飞行能够带来明显的升阻比收益。

菱形双翼是一种典型的超声速翼型，本文利用有益干扰理论，围绕二维菱形双翼超声速布局开展升阻比优化分析研究。

1 基于有益干扰理论的双翼布局方案

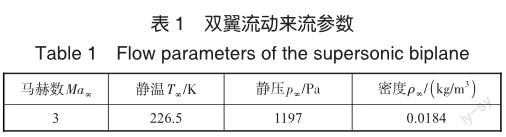
菱形双翼由上下两个菱形翼组成，下文参数中角标a表示下翼的相关参数，角标b表示上翼的相关参数，在二维菱形双翼的主要外形参数中，能够影响菱形双翼气动特性的参数主要有菱形翼的弦长xi（i = 1，2，3）及厚度i，两翼的迎角αa，？？？αb，以及两翼之间的相对位置μn/（MHz？μ-1？s-1）。本文以固定弦长、固定厚度的菱形双翼为研究对象，分析来流马赫数为3、飞行高度为30km的菱形双翼气动布局优化，利用有益干扰理论以及激波-膨胀波理论分析获取优化后的相对位置及迎角，两翼的弦长为c=ca=cb=1？m，厚度为b=ba=bb=0.1m，具体来流参数见表1。

提高升阻比的途径主要有减阻和增升两种，双翼流动中，可以利用两翼之间的激波/膨胀波等流动干扰实现减阻或增升的效果。头部斜激波产生的高压区可以用于产生有益干扰，当这个高压区作用于另一个双翼的后半部分时，波后高压能够减小压差带来的阻力，进而提高升阻比。利用这种思路提高升阻比的方案示意图如图2所示，图中实线代表激波，单虚线代表膨胀波，双虚线代表滑移线。需要指出的是，为了简化表达，在图中表达波系的几何关系时，仅采用单虚线表示膨胀波。

图2为减阻方案的流场设计，下翼前缘斜激波产生的高压区位于（2）位置，高压区间接作用于上翼的后半部分，位于（4）位置；同时，上翼前缘的斜激波产生的高压区（1）间接作用于下翼的后半部分，位于（3）位置。（3）和（4）两处流场的压力增大，将减小这两处的压差阻力。从激波/边界层干扰角度，上下两翼分别产生头部斜激波，斜激波后压力升高，头部斜激波在两翼中间相交，上下两道斜激波波后的区域分别为（9）和（10），压力再次升高。从相交点向下游拖出一道滑移线，滑移线两侧压力相同，马赫数不同。由于流道扩张，经历过相交的两道斜激波分别在上下两翼的中点处反射出膨胀波，压力有所降低，但仍比来流的压力高。

减阻方案中头部斜激波的波后高压区作用于两翼的后半部分，高压区作用在上翼后半部分时能够产生额外的升力，而作用在下翼后半部分时能够产生额外的负升力。充分利用作用于上翼的有益高压，并令下翼避开高压区从而避免产生负升力，令上翼头部斜激波打在下翼的后缘，使下翼刚好脱离上翼产生的高压区，如图3所示，上翼后部高压将为上翼提供额外的升力，而下翼后方区域的高压则不会使总升力减小。

图3所示的增升方案利用的有益干扰思路以上翼增升为主。下翼头部产生的斜激波波后高压区（2）作用于上翼后半部的（4）区域，产生升力，上翼头部产生的斜激波与下翼表面始终没有相交，因此下翼的气动特性几乎没有受到上翼流动的影响。上下翼之间仍会出现斜激波相交后产生的高压区（9）和（10）及滑移线。

2 基于激波—膨胀波理论分析的双翼气动力特性优化

2.1 菱形双翼的气动特性快速预测方法

现有求解超声速翼型气动特性的无黏理论分析方法有线化理论、二级近似理论、激波-膨胀波理论等[21]。其中线化理论和二级近似理论都是采用薄翼理论推导出来的，从本质上无法描述上下两翼之间的流动干扰。因此，本文采用激波-膨胀波理论推导并分析菱形双翼的气动力特性。

本文所研究的菱形双翼共计8个面，这8个面所在的空间位置及编号如图2和图3所示，利用激波-膨胀波理论能够推算出所有面所在流场的压力，压力在菱形双翼表面的积分即为菱形双翼所受的合力，即可以利用激波-膨胀波理论推算出菱形双翼总体升力和阻力。在波系的几何分布估算中使用了如下简化：不考虑激波与膨胀波相交发生的激波局部变形。

在本文的研究中，菱形双翼的弦长和厚度为固定值，将上下菱形翼的前后缘翼尖角度的一半记为θ，有θ= arctan（b/c），针对不同迎角，分析不同迎角组合下的总升力及总阻力。求解流场的顺序从来流方向开始，利用激波-膨胀波的波前波后关系分析各处流场的气动特性[22]。

当流动遇到斜激波，采用如下方法求解波后的马赫数和压力。

利用上述方法，可以迅速预测不同上下翼迎角和相对位置菱形双翼的气动特性干扰特性。

2.2 双翼气动力特性优化

激波-膨胀波理论预测效率高，能够用于快速分析双翼气动特性，为气动布局设计提供优化方向，分析αa在（-10°，10°）及αb在（-10°，10°）区间时所有的气动特性结果，统计这些参数组合下的CL和CD值及升阻比，选取其中的最高升阻比参数组合，作为最优位置和姿态。

图4是减阻方案得到的气动力特性随上下翼迎角变化的规律，即图2所描述的上下翼前缘产生的斜激波对应作用于在另一翼中点的流动。在小迎角变化范围内，双翼之间的干扰强烈，当下翼迎角αa= 5.58°，上翼迎角αb= 5.49°时，能够产生最大的升阻比。当上下两翼都为负迎角时，升阻比为负值，并且存在极小值。

此外，图4显示，升阻比等值线在整个图像中展现出一定的对称性，存在一条斜率为-45°、过零点的零升阻比线，说明对于所有相对水平线对称的布局，升阻比都为0。从图中还可以看到斜率为45°的一条零值线，该零值线说明，当上下翼迎角差为某一特定值时，升阻比为0。升阻比大于0的区域显示，当上下翼的迎角之和大于0°，且上下迎角差小于某特定值时，能够产生正升力。当上下迎角之和小于0°，且上下迎角差大于某特定值时，也能够产生正升力。前者的升力主要由迎角产生的升力主导，后者的升力主要由下翼斜激波波后高压区作用在上翼后部产生。

对于图3表示的增升方案，本文也做了不同迎角的升阻比分析，如图5所示，增升方案中升阻比的最大值出现在αa=0.12°，αb=4.17°組合时。图中升阻比的零值线位于横轴附近，当αb>0°时，大部分区域的升阻比都为正值，当αa较大时，即使αb为负值，也能够产生正升力。值得注意的是，由于这种方案的设计思路是利用波后高压使上翼增升，因此，即使有时αa和αb都为负值，也能够产生正升力，增升方案有助于提高双翼整体的升力及升阻比。

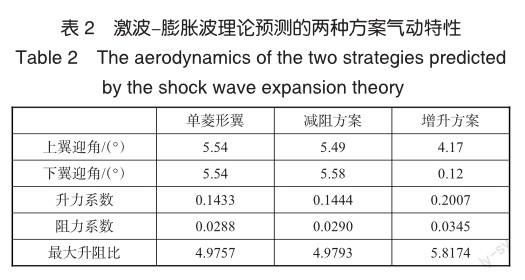
表2统计对比了不同优化方案的升阻比结果。表2中第一列为单菱形翼最大升阻比对应的气动特性统计。减阻方案能够实现的最大升阻比相比于单菱形翼的结果略大，达到最大升阻比时双翼的阻力系数比单菱形翼的阻力系数大，升力系数比单菱形翼的升力系数大，减阻方案对升阻比的提升能力有限。增升方案的升阻比结果相比减阻方案及单菱形翼提高了约17？%。从最大升阻比对应的升力系数来看，升力系数相比另两个方案提高了约40？%。增升方案中阻力系数相比另两个方案有较大增长，从机翼后部减阻效应角度分析该现象产生的原因，增升方案中上翼头部的斜激波波后高压区与下翼不相交，下翼后半部分不增压，没有减阻效应，所以阻力系数变大。整体来看，增升方案能够获得更大的升阻比。

3 增升方案气动力优化方案流场特性分析

3.1 无黏二维双翼流场特性

通过求解可压缩欧拉方程得到的流场结果与激波-膨胀波理论预测得到的结果比较接近，本节采用Fluent软件求解可压缩欧拉方程，对上文中升阻比最大的增升方案流场开展模拟研究，验证激波-膨胀波理论预测的准确性，分析二维空间流场特性。模拟采用三阶MUSCL格式进行空间重构，壁面为绝热壁面条件，二维双翼模型的网格量为nx×ny= 46800。

图6对比了激波-膨胀波理论和无黏模拟得到的波系结果。图中灰色云图部分表示模拟得到的激波、膨胀波结构，上下菱形翼的4个迎风面均产生了斜激波，双翼之间的斜激波相遇后发生激波相交，相交后斜激波的激波角发生变化，两道斜激波之间，从交点位置向下游拖出一道滑移线。利用第2节的理论分析方法，可以获得流场中的激波位置及激波角大小，图中红色虚线标记的是激波-膨胀波理论分析得到的激波角的大小，理论分析出的激波位置与数值模拟得到的激波位置完全相同。上下两翼4个中点均产生了膨胀波，其中两翼中间的膨胀波与斜激波、膨胀波与膨胀波发生相互干扰。双翼的尾部出现了三道斜激波、一道膨胀波，从上下两翼的尾部各拖出一道滑移线隔开了几个波后区域。

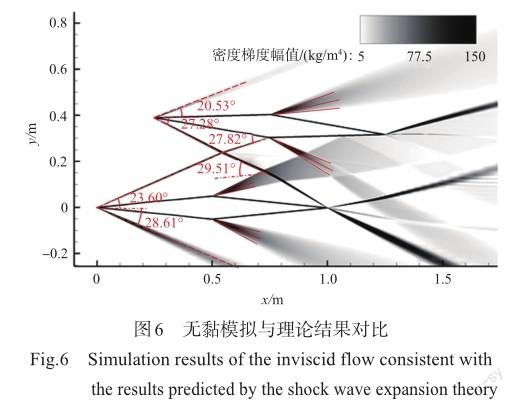
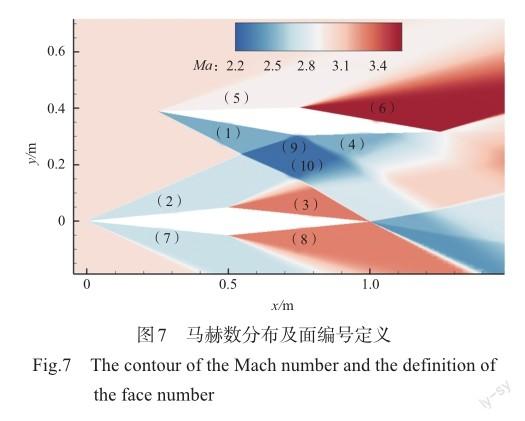
图7和表3对比了数值模拟和激波-膨胀波理论预测得到的马赫数分布结果，表3的数据显示，数值模拟结果和理论预测结果一致。图7的马赫数分布云图显示，面（1）、面（2）、面（5）、面（7）、面（9）、面（10）在斜激波后，波后的参数较均匀。面（3）、面（4）、面（6）、面（8）在膨胀波后，波后参数都经历了气动参数缓变的过程，在统计马赫数时，采用距离膨胀波较远、马赫数变化小的位置处的马赫数进行统计，其结果与理论分析得到结果相同。由于面（1）、面（2）、面（7）前方的头部斜激波比较强，马赫数下降较大，面（5）前方的头部斜激波较弱，马赫数下降较小，编号为（1）、（2）的两面之间的斜激波相交后，面（9）、面（10）的马赫数继续下降。由于面（3）、面（4）、面（6）、面（8）是膨胀波的波后区域，所以马赫数会增大。

压力差是产生升力、阻力的主要来源，图8描述的是增升方案中最大升阻比方案的压力分布云图。在两翼中间的流场，上翼前半部分由于其头部斜激波的压缩，会在斜激波波后形成高压区。上翼后半部分本应受到上翼中点位置膨胀波的影响，形成低压区，但由于下翼头部斜激波产生的高压区作用于上翼的后半部分，导致上翼后半部分这一区域压力增大，上翼后半部分的高压区使上翼产生额外的升力，从而有效提高了双翼整体的升阻比。由于上翼的头部斜激波并没有与下翼表面相交，因此下翼不受上翼头部斜激波的影响。此外，最大升阻比方案中下翼的迎角αa=0.12°，由于下翼的迎角较小，下翼产生的升力比较小。

3.2 考虑黏性的增升方案流场特性

激波-膨胀波理论无法考虑黏性产生的影响，黏性会导致壁面附近出现边界层，进而影响整体流场。本节采用数值模拟的方式，分析有黏情况下的流动特性，并对比有黏与无黏气动力结果的差异。在求解过程中，壁面选择绝热无滑移壁面边界条件，动力黏度采用Sutherland公式，重构方式选择三阶MUSCL格式，采用k-ω？？SST湍流模式，總网格量为855600，网格的整体如图9所示，网格上壁面第一层网格的y+< 1，壁面附近的边界层网格如图10所示。

黏性作用下斜激波位置发生了变化，图11为增升方案中升阻比最大时的双翼流场有黏数值模拟结果，图11中密度梯度幅值变化大的位置为激波和膨胀波所在位置。对比图6所示的无黏结果，黏性导致双翼壁面附近流场出现边界层，两个前缘附近的边界层使头部斜激波强度增大，斜激波与壁面之间的激波角变大。下翼前缘产生的斜激波与上翼相交的位置提前，交点位于上翼中点的前方，并产生了一道强反射激波。上翼前缘斜激波的激波角增大，与下翼的后部发生相交，并发生强激波/边界层干扰。

放大上翼中部的激波/边界层干扰流场，如图12所示，此处的激波/边界层干扰产生了尺度较小的流动分离，入射激波与壁面的夹角较大，在发生了激波/边界层干扰后，产生了强度较大的反射激波。

下翼后部的激波/边界层干扰较强，出现了明显的流动分离结构，如图13所示。入射斜激波的激波脚位于分离区的顶端，分离区内的流动马赫数小于1，在亚声速区域内，斜激波退化为压缩波，在超声速区域内，斜激波跟随马赫数的变化出现了偏折。流线在分离区的顶端位置处出现拐折，此处为一道膨胀波，过膨胀波后流动马赫数迅速增大。由于此处的激波/边界层干扰强度大，入射激波和分离点产生的斜激波在超声速区域相交，因此发生了激波/激波干扰。在附点位置产生了另一道斜激波，流线方向随着这道斜激波一同变化，流线方向重新平行于壁面。

激波/边界层干扰将会导致局部压力分布发生变化，双翼整体的压力分布如图14所示。对比图8的无黏模拟结果压力云图，上翼的中部和下翼的后部将会出现压力的波动，产生局部高压，伴随产生下翼后缘附近的激波强度变化。

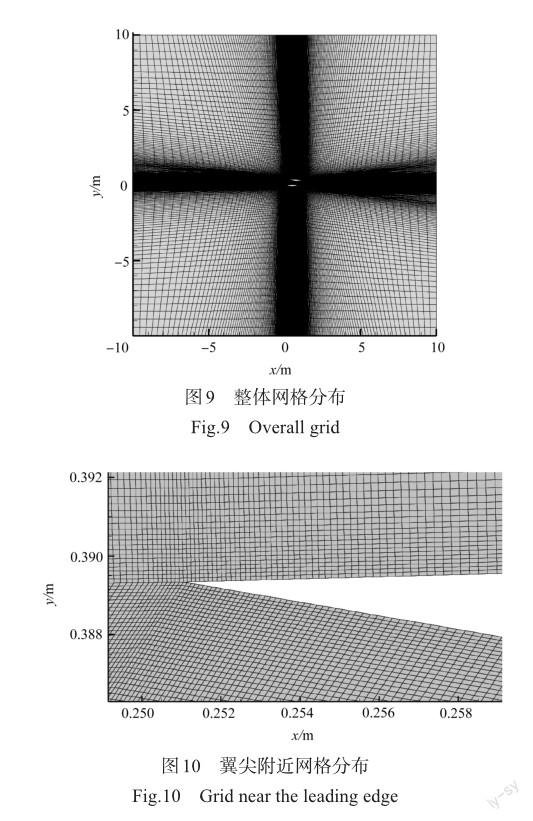
为了能够更加详细地观察上述压力分布特性，图15提取双翼壁面上的压力分布，并用曲线表现压力分布随流向位置的变化规律，图中采用三角形符号标记的曲线为有黏模拟得到的无量纲压力分布，方形符号标记的曲线为无黏模拟得到的无量纲压力分布。由于有黏模拟得到的头部斜激波比无黏模拟得到的斜激波强度高，双翼前半部分的有黏模拟均产生了比理论预测和无黏模拟更大的压力。在双翼后半部分，有黏模拟壁面上的压力仍高于无黏模拟和理论预测结果。需要注意的是，在下翼上翼面的尾部，有黏模拟结果的压力在x=0.83？？～1m位置附近突然增长，黏性作用使下翼的上表面压力合力变大，产生了额外的负升力。有黏模拟中，上翼中部的激波/边界层干扰使局部压力增长，干扰后的压力也比无黏结果大，从而产生额外的正升力。压力曲线包络的面积表示升力的大小，相比无黏模拟得到的结果，有黏模拟预测结果的下翼升力较小，上翼升力较大。

表4总结了激波-膨胀波理论预测、无黏模拟、有黏模拟的气动力结果，其中理论预测得到的升力系数最大、阻力系数最小、升阻比最大；无黏数值模拟得到的阻力系数和理论预测结果几乎相同，但升力系数结果比理论预测得到的结果小，无黏模拟预测的升阻比结果与理论预测结果的误差约为8？%。有黏模拟的升力系数结果比激波-膨胀波理论预测结果小，比无黏预测结果大，这是由于黏性作用使斜激波变强，斜激波波后的压力变大，升力系数增大。有黏模拟得到的阻力系数较大，总阻力由波阻和黏性带来的壁面摩擦阻力组成，因此阻力系数较大。考虑受流场特性影响和黏性影响，升阻比的理论预测结果与带有黏性的数值模拟结果相差非常大，约为29？%。

4 讨论和结论

本文利用有益干扰理论对菱形双翼气动布局开展了升阻比气动特性优化研究，传统双翼布局优化大多不破坏双翼之间平行的位置关系，本文提出了基于上下两翼迎角不同，相对空间位置不同的气动布局优化思路，建立了减阻和增升方案的气动布局。并利用激波-膨胀波理论，设计适用于二维菱形双翼流动的快速气动特性预测方法。在两个优化方案中，机翼之间的相对流向位置和法向位置是由各自迎角决定的，因此以两翼的迎角作为优化变量。

比较两种方案的气动特性后，发现增升方案能够产生更大的升阻比，本文通过求解可压缩欧拉方程验证了激波-膨胀波理论在流场预测中的准确性，分析了双翼升阻比优化后流场中的激波、压力分布等特性。在超声速飞行中，流动黏性不仅会产生壁面摩擦阻力，而且会导致出现边界层，令激波、膨胀波位置偏离理论预测结果，本文采用二维RANS方法模拟双翼在考虑黏性时的流场特性。在黏性的影响下，激波角变大，斜激波与对应翼面相交的位置均发生前移，并产生了明显的阻力系数预测误差，使激波-膨胀波理论预测和湍流模拟预测的升阻比误差达到29%。

超声速双翼流动是经典的流动问题，然而双翼气动布局优化原理尚未得到重视，本文提出的增升、减阻方案能够为双翼布局气动特性优化提供分析思路，本文发展的激波—膨胀波理论预测方法可以作为快速估算气动特性的方法，然而由于预测误差较大，超声速气动布局设计仍需要充分考虑黏性影响。

参考文献

[1]Ferri A， Clarke J H， Lu T. Favorable interference in lifting systems in supersonic flow[J]. Journal of the Aeronautical Sciences， 1957， 24（11）： 791-804.

[2]黄志澄. 论超声速流动中的有益干扰[J]. 空气动力学学报，1992，10（4）： 7. Huang Zhicheng. On the favorable interference in the supersonic flow [J]. ATCA Aerodynamic Sinica， 1992，10（4）： 7.（in Chinese）

[3]Busemann A. Aerodynamic lift at supersonic speeds[J]. Luftfahrtforschung， 1935， 12（6）： 210-220.

[4]Kulfan R. Application of hypersonic favorable aerodynamic interference concepts to supersonic aircraft[R]. AIAA 1978-1458， 1978.

[5]Licher R M. Optimum two-dimensional multiplanes in supersonic flow[R]. Report No. SM-18688， 1955.

[6]劉姝含，朱战霞. 高超声速可变形双翼气动特性[J]. 航空学报，2017，38（9）： 11. Liu Shuhan， Zhu Zhanxia. Aerodynamic characteristics of hy‐personic morphing biplane[J]. Acta Aeronautica et Astronauti‐ca Sinica， 2017， 38（9）： 11. （in Chinese）

[7]刘姝含. 高超声速双翼翼型优化与机翼热气动弹性研究[D].西安：西北工业大学，2017. Liu Shuhan. Research on the optimization of hypersonic bi‐plane airfoil and the aerothermoelasticity characteristics of hy‐personic biplane wings[D]. Xi’an： Northwestern Polytechnical University， 2017. （in Chinese）

[8]华如豪，叶正寅. 基于Busemann双翼构型的超音速导弹减阻技术研究[J]. 应用力学学报，2012，29（5）： 6. Hua Ruhao， Ye Zhengyin. Drag reduction method for supersonic missile based on Busemann biplane concept[J]. Chinese Journal of Applied Mechanics， 2012， 29（5）： 6. （in Chinese）

[9]马博平，王刚，叶坤，等. 基于RBF神经网络和遗传算法的超声速Licher双翼优化设计研究[J].航空科学技术，2019，30（9）： 73-80. Ma Boping， Wang Gang， Ye Kun， et al. Supersonic Licher biplane optimization using radial-basis function neural network and genetic algorithm[J]. Aeronautical Science & Technology， 2019， 30（9）： 73-80.（in Chinese）

[10]Bushnell D M. Aircraft drag reduction：A review[J]. Journal of Aerospace Engineering， 2005， 217（1）： 1-18.

[11]劉荣健，白鹏. 基于超声速有益干扰原理的气动构型概念综述[J]. 航空学报，2020，41（9）： 14. Liu Rongjian， Bai Peng. Concept of aerodynamic configuration based on supersonic favorable interference principle： review[J]. Acta Aeronautica et Astronautica Sinica， 2020， 41（9）： 14.（in Chinese）

[12]Morris O. Aerodynamic characteristics in pitch of several ringwing-body configurations at a Mach number of 2.2[R]. NASA TN D-1272， 1962.

[13]Morris O A， Lamb M. Aerodynamic characteristics in pitch of a modified half ring wing body combination and a swept wing body combination at Mach 2.16 to 3.70[R]. NASA TM X-1551， 1968.

[14]Morris O A， Mack R J. Aerodynamic characteristics of a parasolwing-body combination utilizing favorable lift interference at Mach numbers from 3.00 to 4.63[R]. NASA TN D-4855， 1968.

[15]Cui Kai， Li Guangli， Xiao Yao， et al. High-pressure capturing wing configurations[J]. AIAA Journal， 2017， 55（6）： 1-11.

[16]楚亮. 联结翼布局气动/结构/隐身一体化设计方法[J]. 航空科学技术，2011（2）： 57-60. Chu Liang. Integration design of aerodynamic， structure and stealthy performance for joined-wing[J]. Aeronautical Science& Technology， 2011（2）： 57-60. （in Chinese）

[17]Goto Y， Obayashi S， Kohama Y. Wave drag characteristics of a low-drag supersonic formation flying concept[J]. Journal of Aircraft， 2007， 44（2）： 675-679.

[18]Goto Y， Jeong S， Obayashi S， et al. Design space exploration of supersonic formation flying focusing on drag minimization[J]. Journal of Aircraft， 2008， 45（2）： 430-439.

[19]Rütten M， Trenker M， Rosemann H. Formation flight aerodynamics of oblique flying wing type aircrafts[C]. 6th European Congress on Computational Methods in Applied Sciences and Engineering （ECCOMAS）， 2012.

[20]Nangia R， Palmer M， Blake W， et al. Supersonic aircraft formation flying to increase flight efficiency[C].International Congress of the Aeronautical Sciences， 2008.

[21]钱翼稷. 空气动力学[M]. 北京：北京航空航天大学出版社，2004. Qian Yiji. Aerodynamics[M]. Beijing： Beihang University Press， 2004. （in Chinese）

[22]Xu Yizhe， Xu Zhiqi， Li Shaogang， et al. A hypersonic lift mechanism with decoupled lift and drag surfaces[J]. Science China： Physics， Mechanics and Astronomy， 2013， 56（5）： 981-988.

Research on the Supersonic Favorable Aerodynamic Interference in Diamond-shaped Biplane Airfoil Design

Xue Yifei， Zeng Honggang， Cheng Siye

Chinese Aeronautical Establishment， Beijing 100029， China

Abstract： Favorable aerodynamic interference can lead to lifting enhancement/drag reduction benefiting from the interactions between the aircraft’s configurations. The favorable aerodynamic interference is feasible to obtain a higher lift drag ratio and has good application foreground. The original model was a two-dimensional diamond-shaped biplane airfoil at Mach 3. The drag reduction and lift enhancement strategies were proposed using the high pressure beneath the oblique shock induced by the leading edge. The drag reduction strategy set up the high-pressure impact on the aft body of both airfoils. The lift enhancement strategy set up the high-pressure impact on the aft body of the upper airfoil. The rapid aerodynamics prediction method in this paper used the shock expansion theory. Following the drag reduction and lift enhancement strategies， the paper optimized the lift drag ratio by changing the location and the angle of attack of two airfoils. The lift enhancement strategy can reach a higher lift drag ratio with an increment of up to 17%. Furthermore， the paper analyzed the mechanism of the external lift in the lift enhancement strategy using the two-dimensional simulation method. Viscous is not negligible in the prediction of lift drag ratio. Compared with the shock wave expansion theory， the lift drag ratio obtained by the simulation of the viscous flow is reduced by 29%. The favorable aerodynamic interference and the shock expansion theory are practical for aerodynamic optimization. In addition， the diamond-shaped biplane airfoil provides a potential aerodynamic configuration for supersonic aircraft design.

Key Words： diamond-shaped biplane airfoil； aerodynamic configuration； shock wave； optimization； lift drag ratio