3T1R解耦并联机构动力学与惯量耦合特性分析

朱小蓉 赵 磊 沈惠平

(常州大学机械工程学院,常州 213164)

0 引言

四自由度(3CRR/R)&CRU并联机构,是对Quadrupteron机构进行结构降耦所得[1-2],机构具有运动解耦、耦合度低、工作空间大、转动能力强等特点,在装配、包装及码垛等高速运动工程领域有较好的应用前景。

良好的动力学性能是高速运动并联装备的重要保证。目前并联机构动力学建模主要有拉格朗日法[3-4]、虚功原理[5-8]、牛顿-欧拉法[9-14]等方法,其中牛顿-欧拉法因为概念清晰、关节支反力/力矩可由平衡方程递推获得而得到了广泛应用。LI等[9]基于牛顿-欧拉法对一种4自由度SCARA型并联机构进行动力学建模,以单驱动关节的驱动力最小为优化目标实现了机构的尺寸综合。王庚祥等[10]将机构的关节摩擦力视为非保守内力,采用牛顿-欧拉法建立了含恰约束支链4-SPS/CU并联机构的动力学方程,推导出关节的约束反力/力矩,并讨论了关节摩擦对机构驱动力的影响。冯志友等[11]采用牛顿-欧拉法对2UPS-2RPS并联机构进行动力学建模,讨论了给定动平台运动规律和外力条件下的机构驱动力和约束力矩。CHEN等[12]基于牛顿-欧拉法,通过设置兼容方程,建立了一种过约束并联机构的动力学方程,并以驱动力最小为优化目标进行动力学性能优化。GUO等[13]考虑球关节、万向节和滚珠丝杠的摩擦效应,采用牛顿-欧拉法建立了5自由度混联机器人的显式动力学模型。

并联机构的闭环多分支结构特征导致了支链之间存在较强的耦合,影响机构高速、重载运动时的动态性能。TOURASSIS等[15]提出了机器人动力学方程中惯量矩阵的中心地位,解释了惯量矩阵的结构特征及物理意义,并以串联机器人为例引入惯量耦合系数对机构动力学特性进行评价。ASADA[16]利用惯量椭球来表征刚体的动力学特性。这种基于惯量的动态指标已逐渐推广到并联机器人的动力学性能评估和参数优化,研究工作主要集中在耦合惯性矩阵的分析方面。LIU等[17]对Stewart平台的惯性矩阵进行解耦,以惯性矩阵的最大特征值作为惯性指标,对Stewart平台进行尺寸优化。宋轶民等[18]定义系统惯性矩阵条件数的倒数为评价系统动力学性能的局部指标,对非冗余3-RRR和冗余4-RRR平面并联机构的动力学性能进行了比较。王冬等[19]定义机构惯量矩阵的非对角元素之和作为惯量耦合指标,以3-PRS并联机构为例,分析了耦合指标在工作空间内的分布,并用实验进行了验证。文献[20-23]提出了统一量纲的惯量耦合强度指标,研究了评价指标随机构运动状况的变化规律。WU等[24]提出了任务空间中各向同性的动态性能指标,综合考虑了动力学模型中加速度、速度、重力等影响因素,并以4自由度机器人为例验证了性能指标的有效性。

肾结石治疗方法较多，主要分为保守治疗、腔镜治疗和手术治疗。保守疗法通常无法获得理想效果。开放手术会对患者造成较大创伤，术后恢复时间长，诸多肾结石患者对于此种治疗方法不认可[4-5]。在随着泌尿外科微创技术的快速发展，肾结石治疗方案中的微创腔镜手术获得广泛应用，同开放手术方法进行比较，术中出血量、手术创伤以及术后并发症等方面均呈现出显著优势。

本文基于牛顿-欧拉法,考虑构件重力以及外负载建立(3CRR/R)&CRU并联机构的逆向动力学模型,并利用有限元仿真验证模型的正确性。基于关节空间的惯量矩阵,建立支链间惯量耦合强度评价指标,分析其在工作空间内的分布规律,并与结构降耦前的机构进行对比分析。

1 机构描述及运动学分析

1.1 机构描述

(3CRR/R)&CRU机构的结构简图如图1所示,可看成由两个子结构并联而成。动平台2一方面通过C41R42U43支链直接与静平台0相连;另一方面通过转动副RD、中间平台1及3条CRR支链与静平台0相连,其中3条CRR支链相互正交,分别沿x、y、z轴安装。与Quadrupteron机构相比,该机构由两个基本运动链组成,不仅耦合度降低、运动学解耦,而且全工作空间内所有位置的转动能力一致[1],克服了一般并联机构耦合度强、控制复杂的弱点。

机构的4个驱动副分别安装在间距为L的4个轨道上。在固定轨道上点O建立静坐标系Oxyz,该机构的末端动平台2能够实现x、y、z3个方向的移动以及绕垂直方向轴线的转动。

设机构输入矢量为(ρ1,ρ2,ρ3,ρ4),末端输出点D的位姿为(xD,yD,zD,φ),其中φ为动平台的姿态转角。h为中间平台和动平台之间的高度差,动平台长度为l,转动副Ri3在中间平台的安装基点为点Ci,分布在半径为r的圆周上,以中间平台点N为原点建立图2所示坐标系Nuvw,w轴垂直于中间平台,NCi与u轴的安装角为βi。机构定长杆AiBi、BiCi杆长分别为li1、li2(i=1,2,3,4);杆件AiBi、BiCi转动角分别定义为θi1、θi2(i=1,2,3,4)。

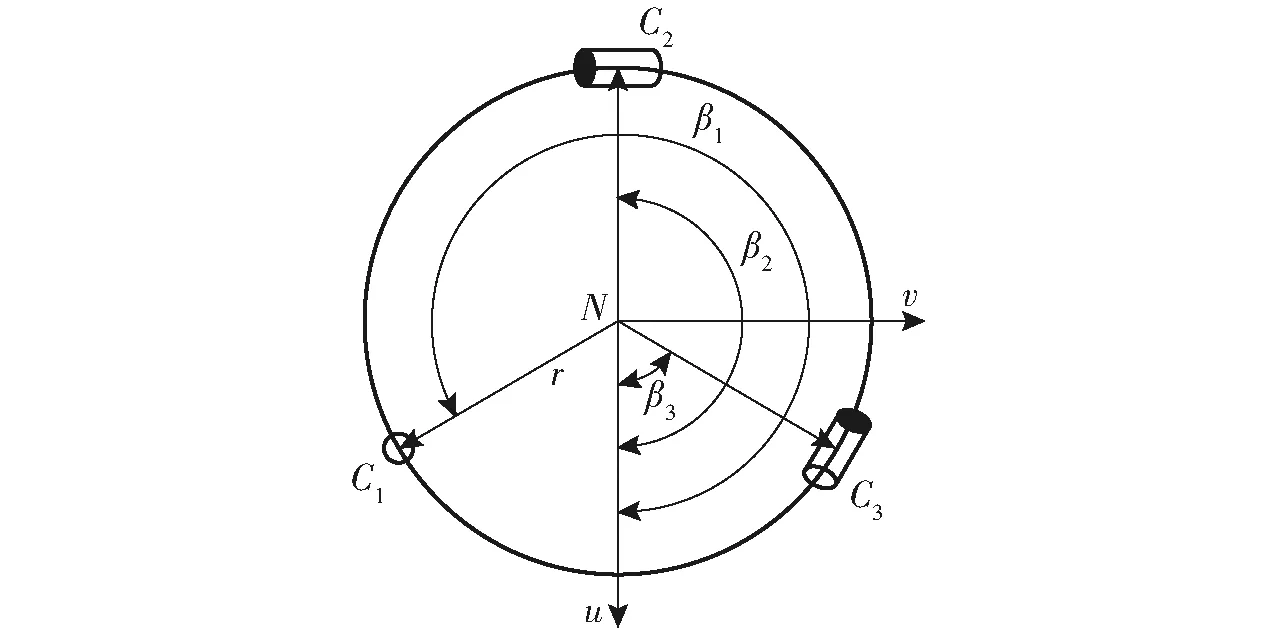
图2 运动副在中间平台1上的分布

机构支链1、2、3、4存在的运动学关系分别为

对里程桩号4+845～4+995段使用TGP 206A超前地质预报处理软件处理原始地震波三分量原始数据(图8)后得到同侧地震波绕射偏移图(图9)和同侧地震波反射界面图(图10)。

(1)

(2)

(3)

(4)

式中,c表示余弦函数;s表示正弦函数。

1.2 机构位置正反解

为验证所建动力学模型的正确性,采用ADAMS软件对机构进行仿真验证。通过设置环境参数和单位系统并添加相应的运动副约束,虚拟样机模型如图9所示。

1、设计总工程师要紧紧把握总布置设计专业，并作为搞好工程设计质量、降低工程造价的重要环节之一来抓。从工程开始就要重视电厂的总体规划和全厂总布置工作，从总体规划入手，搞好工程设计质量，认真贯彻电力建设“安全可靠、经济适用、符合国情”的十二字方针。

(5)

机构位置正解方程为

(6)

由式(5)、(6)可知,机构x、y、z方向的移动输出与3支链的驱动输入ρ1、ρ2、ρ3存在一一对应关系,且互相之间独立,转动输出仅与ρ2、ρ4相关,故机构具有运动学解耦特性。

1.3 动平台速度和加速度

对式(6)关于时间求导,可得

(7)

其中

1.4 中间平台速度和加速度

根据动平台与中间平台的位置关系,以及机构的位置正反解方程式(5)、(6),可得中间平台几何中心在坐标系Oxyz系下的矢量表示为(x1,y1,z1),其中

(8)

ri3、ri4——点Bi、点Ci相对于质心的位置矢量

1.5 驱动杆AiBi速度和加速度

由式(1)～(4)可推导得

Misθi1+Nicθi1=Ki(i=1,2,3,4)

(9)

其中

(10)

(11)

(12)

(13)

对式(9)求解,可得杆AiBi转动角为

(14)

则杆件AiBi质心速度和角速度为

(15)

(16)

式中eAiBi——点Ai到点Bi的单位向量

vAi、vBi——点Ai、Bi在静坐标系中的速度

那天晚上两人睡在了一起，好友抱着女人跟她说，有些时候咱们女人是最傻的，被骗了还不醒悟，被抛弃了还怀念人家过去的好，想一想真的很傻。

(17)

(18)

1.6 被动杆BiCi速度和加速度

同样,杆BiCi质心的速度和角速度为

(19)

(20)

对式(19)、(20)求导,可得杆BiCi质心加速度和角加速度为

对于”罗森塔尔效应”，大家是熟知的，这就要求我们教师在教学中要帮助学生树立学习信心。学生的学习信心不足，怀疑自己的学习潜力，自卑心强，就不可能对学习产生兴趣。如果有了教师的信任和爱护，学生则会变得更加自信、自强。对学习信心不足的学生，教师要善于发现和利用他们的闪光点，及时表扬和鼓励，以增强其信心。学生经常受到激励和鼓舞会产生愉悦的心理体验，从而产生浓郁的学习兴趣。

(21)

(22)

2 并联机构动力学模型

采用牛顿-欧拉法建立机构的动力学模型,分别以运动构件和动平台为研究对象进行受力分析。为简化模型做如下假设:①构件及动平台为质量集中分布的刚体单元,构件几何中心与其重心重合,重力矢量在z轴负方向。②动平台所受外载荷简化为过其几何中心的力Fex和力矩Mex。③与机架相连的移动副为驱动副,采用伺服电机+减速器+滚珠丝杆副的驱动形式。

（5）随着不断巡检数据的增加，能够具备自动更新设备历史状态信息库，更新状态模型，动态、灵活地调整和控制设备运行状态，使系统状态往有利方向发展。

2.1 子结构1中各运动构件

子结构1由3条相同的CRR支链并联而成,应分别进行受力分析。

2.1.1驱动杆AiBi受力分析

驱动杆AiBi(i=1,2,3)两端分别通过圆柱副和转动副与定平台 (包括驱动装置) 和被动杆BiCi相连,受力如图3所示。

在圆柱副处驱动杆受力Fai=(Faix,Faiy,Faiz)和力矩Mai=(Maix,Maiy,Maiz)作用,在转动副处受杆BiCi的约束力Fbi=(Fbix,Fbiy,Fbiz)和约束力矩Mbi=(Mbix,Mbiy,Mbiz),以及连架杆自重mi1g。其中,Fa1x、Fa2y、Fa3z分别为作用在支链1、2、3丝杆螺母上的主驱动力,记为τ1、τ2、τ3。又根据支链布局,约束力矩可分别记为Ma1=(0,Ma1y,Ma1z)、Ma2=(Ma2x,0,Ma2z)、Ma3=(Ma3x,Ma3y,0)、Mb1=(0,Mb1y,Mb1z)、Mb2=(Mb2x,0,Mb2z)、Mb3=(Mb3x,Mb3y,0)。

则杆AiBi力平衡方程为

(23)

式中O——零矩阵

在固定坐标系下对杆AiBi质心取矩,得力矩平衡方程为

(24)

其中

仔猪白痢的病理变化主要表现在可视粘膜苍白、消瘦、肠粘膜充血、轻度出血、肠壁薄且失去弹性、肠内容物增多呈泡沫样，肠系膜淋巴结肿大及充血。

Mi1=Ii1εi1+ωi1Ii1ωi1

式中Mi1——杆AiBi惯性力矩

Ii1——杆AiBi相对于质心的转动惯量

ri1、ri2——点Ai、点Bi相对杆质心的位置矢量

其中

2.1.2被动杆BiCi受力分析

这三个环节从整体上决定了一个企业的品牌能不能做起来，能不能被公众认可，而企业品牌建设的长期规划也是围绕着这三个环节展开和操作的。在这个过程中，品牌价值的评估是企业有条不紊地进行品牌建设的重要一环，可以帮助企业实时掌握自身品牌建设的效果，及时做出分析与战略调整。

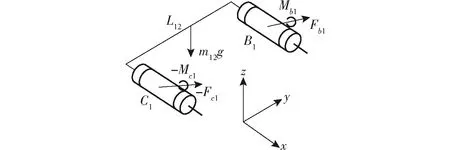
图4 杆件BiCi的受力分析

则杆BiCi力平衡方程为

磷石膏是磷化工企业采用湿法工艺，在磷酸生产中用硫酸处理磷矿时产生的固体废渣，其主要成分为二水硫酸钙，此外还含有未分解完的磷矿、氟化物、磷酸、有机质、酸不溶物、铁铝化合物等杂质。[1]通常情况下，湿法生产1t磷酸就会副产4.5-5.5t磷石膏。[2]

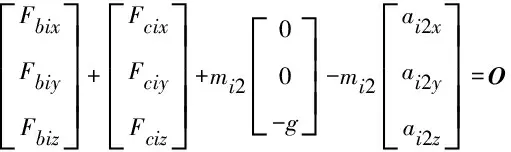
(25)

对杆BiCi质心取矩,得力矩平衡方程

(26)

其中

Mi2=Ii2εi2+ωi2Ii2ωi2

式中Mi2——杆BiCi惯性力矩

Ii2——杆BiCi相对于质心的转动惯量

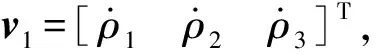
2.1.3中间平台受力分析

中间平台受力包括3个转动副Ri3处的反力-Fci和约束反力矩-Mci,以及转动副RD处的约束力Ft1=(Ft1x,Ft1y,Ft1z)和约束力矩Mt1=(Mt1x,Mt1y,0),以及自身重力m1g,见图5。

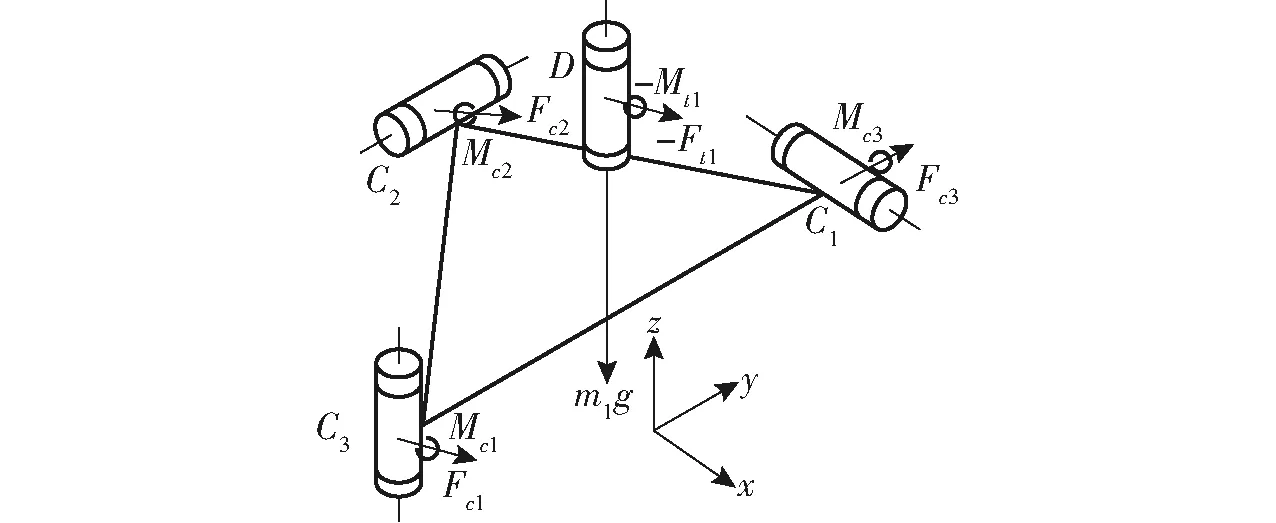
图5 中间平台受力分析

中间平台力平衡方程为

(27)

由于中间平台仅有移动,只产生惯性力,在定坐标系下对质心的力矩平衡方程为

(28)

式中rci——点Ci相对于中间平台质心点D的位置矢量

2.2 子结构2运动构件

2.2.1驱动杆A4B4受力分析

驱动杆A4B4在圆柱副C41处受力Fa4=(Fa4x,Fa4y,Fa4z)和约束力矩Ma4=(Ma4x,0,Ma4z);转动副R42处受约束力Fb4=(Fb4x,Fb4y,Fb4z)和约束力矩Mb4=(0,Mb4y,Mb4z),以及自重m41g,如图6所示。其中,Fa4y为支链驱动力,记为τ4。

图6 驱动杆A4B4受力分析

则杆A4B4的力平衡方程为

(29)

对杆A4B4质心取矩,得力矩平衡方程为

(30)

其中

M41=I41ε41+ω41I41ω41

式中M41——杆A4B4惯性力矩

I41——杆A4B4相对于质心的转动惯量

r41、r42——点A4、点B4相对质心位置矢量

杆BiCi(i=1,2,3)两端均以转动副与驱动杆AiBi和中间平台连接,受到驱动杆的反力-Fbi和反力矩-Mbi,受到中间平台的约束力Fci=(Fcix,Fciy,Fciz)和约束力矩Mci(支链1、2、3分别记为Mc1=(0,Mc1y,Mc1z)、Mc2=(Mc2x,0,Mc2z)、Mc3=(Mc3x,Mc3y,0)),以及杆件自重mi2g,受力如图4所示。

2.2.2被动杆B4C4受力分析

被动杆B4C4在虎克铰U43处受动平台的约束力Ft2=(Ft2x,Ft2y,Ft2z)和约束力矩Mt2=(Mt2x,0,0),在转动副R42处受反力-Fb4和约束反力矩-Mb4,以及杆件自重m42g,如图7所示。

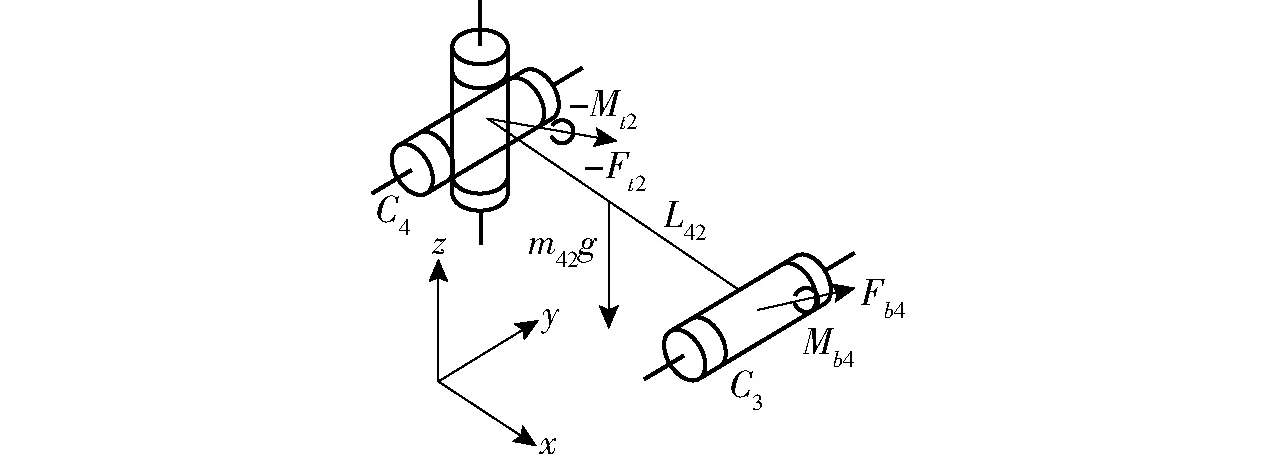
图7 连杆B4C4的受力分析

则杆B4C4的力平衡方程为

如果短期燃油修正值在图2所示“3”区域(-35%～-60%)或在“4”区域(+35%～+60%)，说明发动机的反馈控制已经无法修正混合汽的状态，此时发动机会激活故障码P0172(混合汽过浓)或故障码(P0171)，同时发动机故障指示灯点亮。

(31)

对杆B4C4质心取矩,得力矩平衡方程

(32)

——坚持以人民为中心的发展思想，始终把维护人民群众资源权益作为各项工作的出发点和落脚点，积极推动资源为民惠民利民，不断健全完善自然资源社会服务体系，人民群众的幸福感获得感持续增强。

对式(15)、(16)求导,可得杆AiBi质心加速度和角加速度为

M42=I42ε42+ω42I42ω42

式中M42——杆B4C4惯性力矩

I42——杆B4C4相对于质心的转动惯量

2017年9月23日，在当地经销商的配合下，召开了农户观摩和部分零售商观摩会暨订货会，成功销售云天化葡萄套餐肥24套。为云天化红宝石套餐肥在山东省招远市红宝石葡萄作物上的推广打下了坚实的基础。

r43、r44——点B4、点C4相对质心位置矢量

2.3 动平台受力分析

动平台两侧分别通过RD和U43与支链相连,受力如图8所示,包括转动副约束反力-Ft1和约束反力矩-Mt1;约束反力-Ft2和约束反力矩-Mt2,外力Fe=(Fex,Fey,Fez)、外力矩Me=(Mex,Mey,Mez);以及自身重力mg。

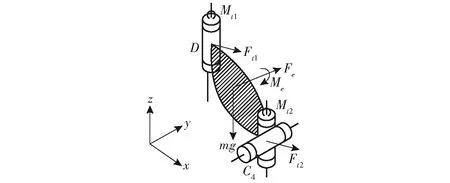
图8 动平台受力分析

则动平台力/力矩平衡方程为

关于“音乐产业”的兴起，可追溯到20世纪80年代左右。随改革开放的深入，音乐形式不断丰富，音乐人才队伍逐渐壮大。以磁带为主的唱片销量突飞猛进，得到空前发展。20世纪末，互联网的普及使数字音乐崛地而起，并占据音乐产业的核心地位。此外，还延伸出许多相关产业，如音乐教育业、音乐生产业等。音乐产业不仅为经济和文化创造出财富，而且极大扩展了文化产业的领域。

(33)

(34)

其中

M=Iε+ωIω

式中M——动平台惯性力矩

I——动平台相对于质心的转动惯量

rD、rC4——点D和点C4相对质心位置矢量

2.4 并联机构动力学方程

联立式 (23)～(34),共60个方程,60个未知量,方程可解。通过消元法消除内力/力矩,可得到机构驱动力的显式表达式,并记驱动力为

τ=[τ1τ2τ3τ4]T=[Fa1xFa2yFa3zFa4y]T

3 动力学数值算例

3.1 动力学模型仿真验证

由式(1)～(4)可得机构位置反解方程

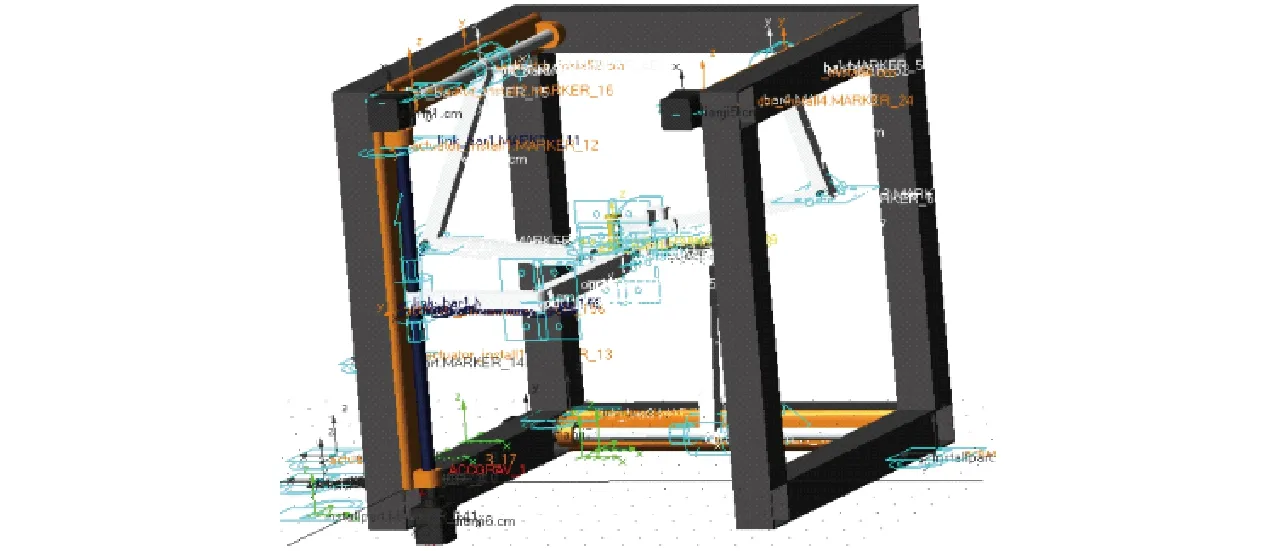
图9 ADAMS仿真模型

机构几何和惯性参数如表1所示。为提高理论建模精度,杆件质心、质量和惯量均由仿真模型获得;中间平台和杆件采用碳纤维,驱动系统采用1FL6024-2AF型直流伺服电机和1605型滚珠丝杆。

表1 机构的几何和物理参数

假设外负载为0,动平台姿态角不变φ=0°,初始运动条件下动平台质心坐标为(x0,y0,z0),给定动平台运动轨迹为

(35)

将表1中参数值代入动力学方程,利用Matlab计算各支链驱动力,计算结果与ADAMS仿真软件按同样轨迹仿真运动的结果进行对比,结果如图10 所示。由图10c可知,理论值与仿真值基本吻合,4条驱动力曲线的最大相对误差分别为5.49%、2.51%、8.26%、0.35%,验证了动力学模型正确性。

图10 驱动力计算结果

3.2 加速度对驱动力的影响

对高速并联机构,主要承受来自高速运动产生的惯性力,因此下面分析当动平台最大加速度为3、7、11 m/s2时机构驱动力的变化,并假设外负载为0,动平台姿态角不变φ=0°,沿平行于坐标轴方向和空间直线运动(4条轨迹如图11所示),均采用五次多项式进行路径规划,且初始位置的速度、加速度为0,驱动力计算结果如图12所示,每条支链驱动力最大值见表2。

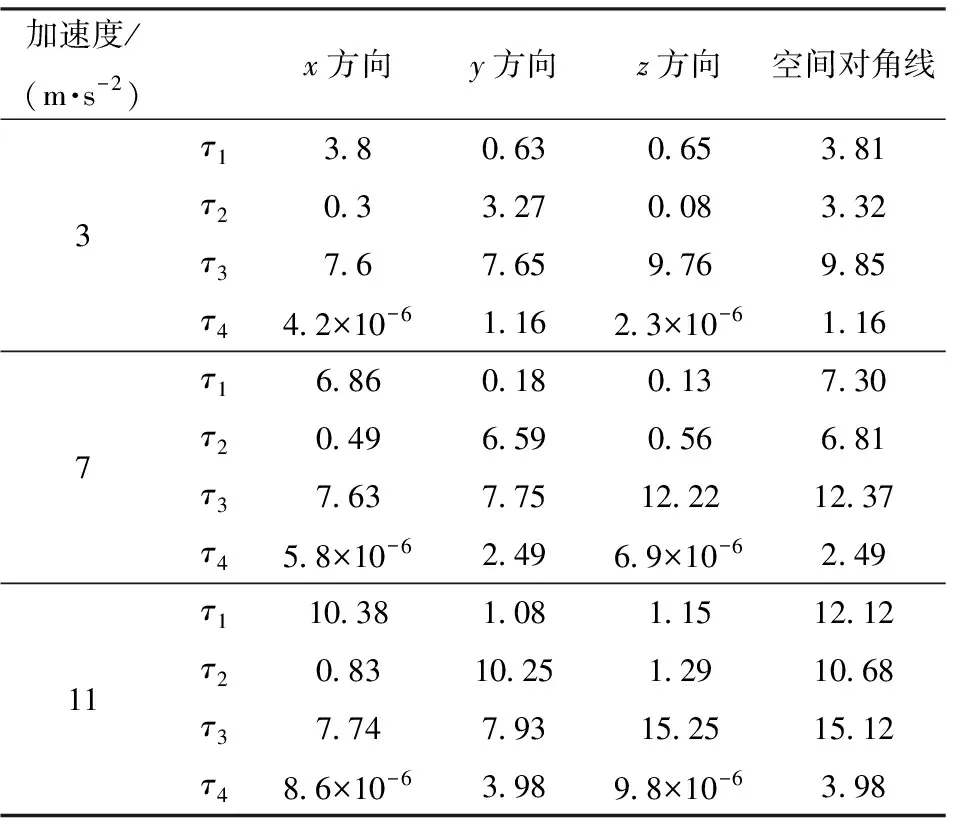
表2 不同加速度时的驱动力

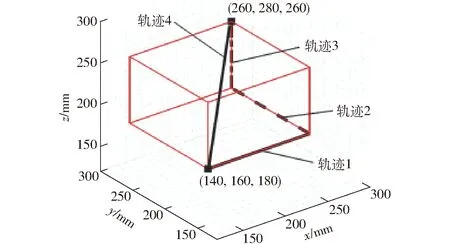
图11 不同运动轨迹

图12 加速度对驱动力的影响

由于机构沿x、y、z轴的运动分别由支链1、2、3的驱动控制,因此当动平台平行于x、y、z轴运动时,支链1、2、3分别定义为驱动支链,其余支链定义为相应的锁定支链。

由图12和表2可得出:

(1)无论沿哪个方向运动,驱动力随动平台加速度的增加而增加。特别是平行于坐标轴方向运动时,驱动支链的驱动力对加速度呈线性增加,但锁定支链的驱动力增加幅度较小。

(2)无论平面运动还是空间运动,支链3的驱动值都较大。沿x、y轴运动时,支链3的驱动力接近甚至超过驱动支链的驱动力,特别是低加速度时更为明显,因此机构结构设计时支链3是关键。

(3)动平台做定姿态运动时,支链4仅与y轴方向的运动有关,当动平台沿x、z轴运动时,支链4的驱动力接近0。

(4)支链间驱动力存在耦合。相同的加速度条件下,空间运动时的驱动力大于单轴运动时的驱动力,且加速度越大,差值越明显,这也证明了惯量对机构动力学性能有较大影响。

3.3 动平台姿态角对驱动力的影响

为研究姿态角对机构驱动力的影响,假设动平台中心点D按图11中轨迹4运动,姿态角分别保持为φ=±60°、±30°、0°时,计算支链的驱动力,结果如图13所示。由图13可得:①当运动轨迹相同时,动平台姿态角的变化对驱动力τ1、τ3没有影响,对τ2、τ4有影响,且影响规律相同。②当姿态角为-60°时,所需驱动力最小,可以将此姿态设置为机构的初始姿态。

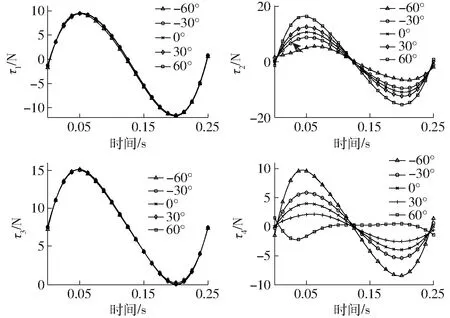
图13 姿态角φ对驱动力的影响

4 动力学耦合特性分析

并联机构笛卡尔空间逆动力学模型可表示为

(36)

式中τ——主动关节的驱动力

MX——机构广义坐标下的惯性矩阵

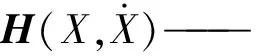
F——外力

对高加减速机构而言,与加速度有关的项MX将起主导作用。对(3CRR/R)&CRU并联机构而言,广义坐标下的惯性矩阵为

(37)

式中M——动平台在广义坐标下的惯性矩阵

M1——中间平台广义坐标下的惯性矩阵

Mi1——驱动杆在广义坐标下的惯性矩阵

Mi2——被动杆在广义坐标下的惯性矩阵

为研究并联机构主动支链间的动力学耦合特性,需要建立其关节空间的驱动力模型。由于机构动能既能在关节空间下表示,又能在广义坐标下表示,则有

(38)

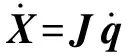
(39)

将式(39)代入式(38),可得到笛卡尔坐标下的惯量矩阵MX与关节空间的惯量矩阵Mq之间的关系为[22]

Mq=(J-1)TMX(J-1)

(40)

根据文献[14],可计算出机构每个构件j在定坐标系下的广义惯量矩阵为

(41)

式中m——构件j质量

R——构件j局部坐标系相对于定坐标系的旋转变换矩阵

I——单位矩阵

M——构件j局部坐标下的惯性矩阵

机构关节空间的惯性矩阵Mq第i行除对角元素外的其他元素Mik(i≠k)为第i支链对其余支链的耦合惯量,会产生耦合力矩从而影响支链的动态性能。基于此,文献[25]提出了并联机构支链间的动力学耦合强度指标DCIi,计算式为

(42)

其中

式中,δDi为耦合强度系数,是惯性矩阵Mq的非对角项相对对角项的占比,值越小表明机构受到的耦合力矩越小。耦合强度指标DCIi是对δDi的进一步处理,使其在[0,1]范围内变化。该值越接近1,动力学耦合越严重,反之,动力学耦合强度越小。由式(42)可知,DCIi为机构位姿的函数。

将表1所示参数依次代入式(41)、(37)、(40)、(42),可得第i条支链的耦合强度指标DCIi在工作空间的变化规律。为便于性能比较,采用同样的方法,对结构降耦前的Quadrupteron机构[1]的耦合强度指标进行计算。图14、15分别为两个机构的DCI在工作空间内的分布,DCI最大值见表3。

表3 机构DCI的最大值

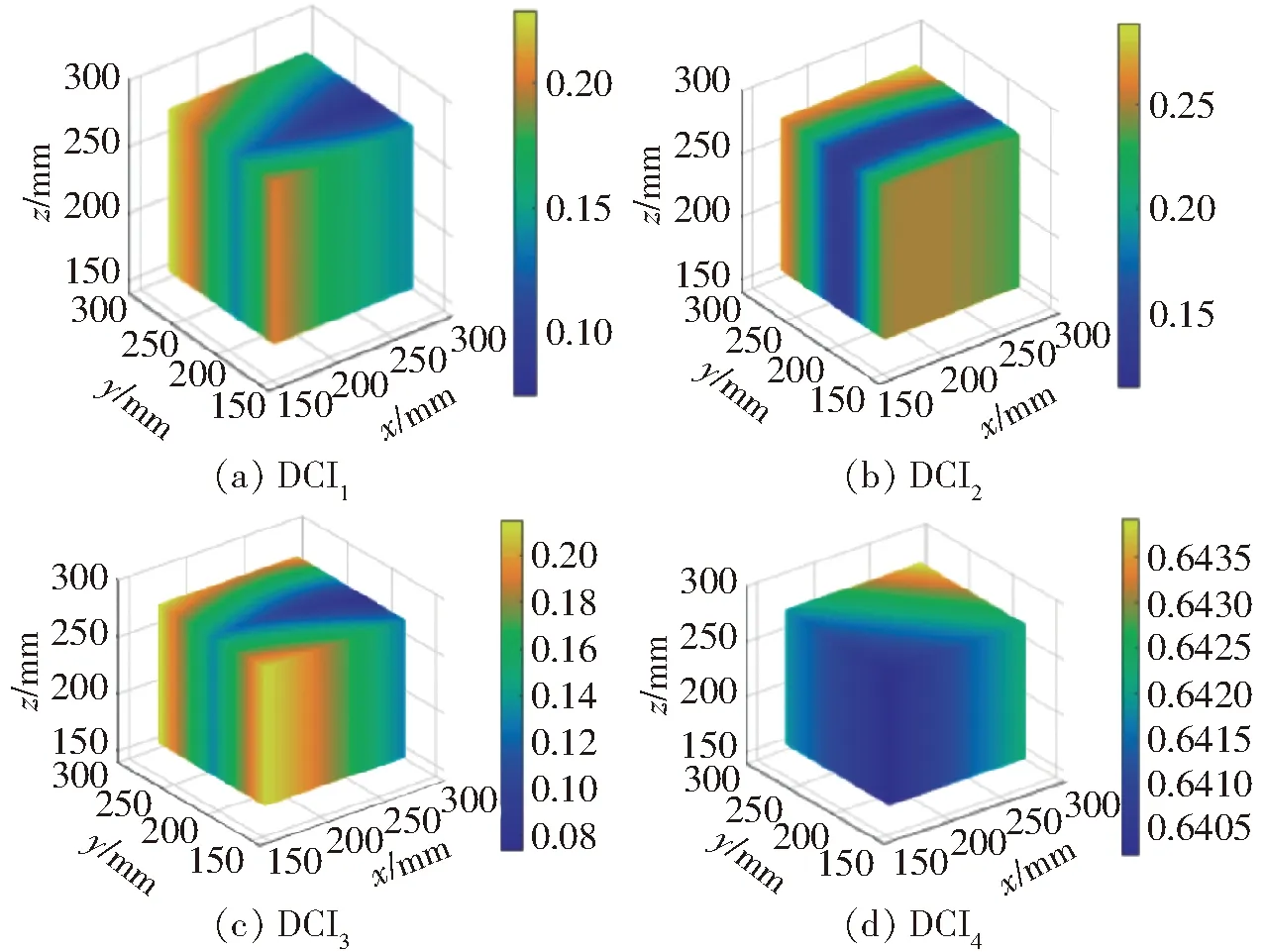
图14 降耦后机构(3CRR/R)&CRU的DCI

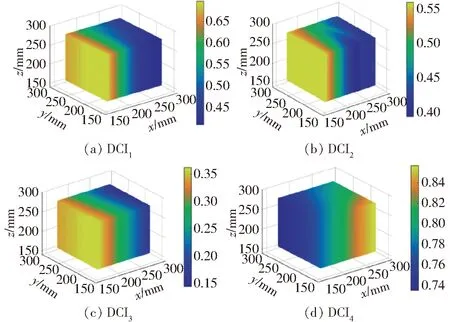
图15 降耦前机构Quadrupteron的DCI

由图14、15以及表3可知:

(1)对所有支链而言,(3CRR/R)&CRU 降耦机构的耦合强度明显低于降耦之前的Quadrupteron机构。DCI1的最大值从0.7降到0.22,DCI2最大值从0.6降到0.26,DCI3的最大值从0.4降到0.24,DCI4的最大值从0.86降到0.64。

(2)运动学解耦可降低机构惯量耦合强度。由文献[26]可知,降耦前机构仅z向输出完全解耦,其余输出为部分解耦,因此机构DCI3明显低于DCI1、DCI2和DCI4。而降耦后机构的3个移动输出完全解耦,转动部分解耦,输出与支链2、4的驱动相关,因此降耦后机构的DCI4高于DCI1、DCI2和DCI3。

为进一步分析降耦之后机构DCI的分布规律,绘制z=260 mm时DCIi在xy平面内的等高线图,结果如图16所示。由图16可知:

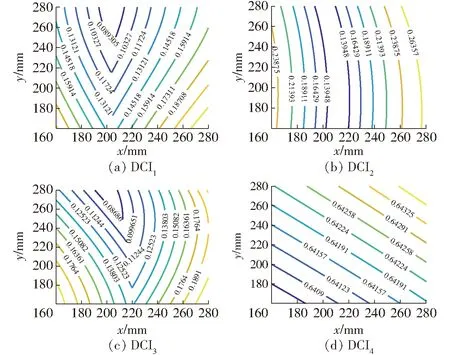
图16 DCI分布(z=260 mm)

(1)降耦机构(3CRR/R)&CRU所有支链的DCI值均很小,DCI1、DCI2和DCI3均低于0.26,说明支链间耦合强度较弱,尤其工作空间中心位置的DCI值达最小。

(2)整个xy平面内DCI值的变化幅度较小,说明机构具有较好的各向同性性能,对高速高精等工程应用更为有利。

5 结论

(1)考虑重力、外负载,利用牛顿-欧拉法建立了(3CRR/R)&CRU并联机构的动力学模型,并用ADAMS进行了仿真验证。

(2)基于所建动力学模型分析了加速度和动平台姿态角对机构驱动力的影响,为机构轨迹规划提供了理论依据。

(3)建立了惯量耦合强度指标,分析了其在工作空间内的分布。结果表明,结构降耦明显降低了机构支链间的耦合强度,提高了机构的动态性能。

(4)降耦之后的机构,不仅惯量耦合强度弱,而且整个工作空间内耦合强度变化较小,提升了机构的各向同性性能。