基于经验小波变换的瞬时谱分析技术及其在致密砂岩气藏检测中的应用
陈伟,杨浪,陈名德,连辰浩,江源
1.油气资源与勘探技术教育部重点实验室(长江大学),湖北 武汉 430100 2.长江大学地球物理与石油资源学院,湖北 武汉 430100
随着全球原油需求日益增长,油田勘探程度不断提升,促使勘探重点转向隐蔽油气藏,该类油气藏受埋藏深度影响,多由致密砂岩组成,具有超高压、超深、低孔、低渗等特点,这对勘探技术带来新的挑战,而瞬时谱分析技术给油气勘探向更深处发展带来希望。地震信号是非线性的、非平稳的信号,它们的能量分布可以通过时频分析获得,因此可以在时域和频域,即联合时频分布中完全建立信号能量或强度的分布。时频分析方法可以观察时域和频域信号的演化,并显示信号的局部时频特征。因此,时频分析方法已被广泛应用于地震波分析中。瞬时谱分析技术应用到地球物理领域中检测油气藏的存在现已成为热点。瞬时谱分析技术主要依赖于时频分析方法的优劣,如今广泛应用的时频分析方法主要分为两类,一类为线性时频分析方法,如Gabor变换,小波变换,S变换等;另一类为非线性时频分析方法,如Hilbert-Huang变换等。
Fourier变换只能将时间域的信号整体变换到频率域,将信号的频率成分和分布表示出来,虽然使信号拥有了频率分辨率,却丢失了时间分辨率,不能反映出信号的频率特征随时间的变化情况。为了解决该问题,GABOR[1]于1946年首次提出在时频域内分解一维信号的方法,即短时Fourier变换。短时Fourier变换中最具代表的为Gabor变换。Gabor变换选取高斯函数作为窗函数,在信号的每一小段时间间隔[2]内进行Fourier变换,该窗口在时间轴上进行平移,对每一段信号进行局部Fourier分析后,再将变换得到的频率信息放到时间-频率的二维平面上,从而得到时频谱。Gabor变换选取高斯函数作为窗函数的优点在于高斯函数的Fourier变换还是高斯函数,不会对变换结果产生不良影响,可以同时提供时域和频域局部化的信息。另外,根据Heisenberg测不准原理,变换得到的结果不能同时拥有极高的时间分辨率和频率分辨率,极大地影响了分析结果的好坏。而高斯函数窗口面积已达到Heisenberg测不准原理的下界,能兼顾时间轴和频率轴的分辨率。Gabor变换的基函数不能成为正交基[3],为保证不丢失信息,只能采用非正交基参与信号分析,使得计算复杂度更高。Gabor变换的窗口固定不变,无法针对高低频信号给出可以调节的时频窗,割断了频率与窗口长度的内在联系[4];对短时突发信号进行分析时,可能产生时间或频率上的模糊现象[5]。MORLET[6]等人从短时Fourier变换中推出小波变换,能对信号同时在时间域和频率域内进行局部化分析。与Fourier变换不同,小波变换有两个变量:尺度和平移量。尺度控制小波函数的伸缩,平移量控制小波函数的平移。尺度就对应于频率(反比),平移量就对应于时间。尺度增大,则时窗伸展,频宽收缩,带宽变窄,中心频率降低,时间分辨率降低而频率分辨率增高;尺度减小,则相反[7]。这符合实际问题中高频信号持续时间短、低频信号持续时间长的自然规律。小波变换能准确反映待测信号的幅频特性。在小波变换中,时频窗口的长度和宽度随着参数尺度的变化而变化[8]。虽然小波变换克服了短时Fourier变换单一分辨率分析的不足,但是由于引入的尺度因子与频率没有直接的联系,且在小波变换中没有明显表现出来,因此小波变换的结果不是一种真正的时频谱。小波分析的另一个问题是其具有的自适应特点,一旦基本小波被选定,就必须用它来分析所有待分析的数据。STOCKWELL等[9]结合短时Fourier变换和小波变换提出S变换,S变换相对于小波变换的不同在于其公式中加入了相位项,用于进行相位校正。它与小波变换一样存在基本小波,其基本小波由简谐波函数与高斯函数相乘组成,其中,简谐波函数在时间域内作伸缩变换,而高斯函数则作伸缩和平移变换[10]。S变换既克服了短时Fourier变换和小波变换的不足,也继承了它们的优点[11-12]。但是S变换的窗函数随频率以固定的趋势改变,基本小波一经选定则无法更改。PINNEGAR等[13]、高静怀等[14]在S变换的基础上提出广义S变换,通过各种可调的属性参数控制窗函数,使其具有更高的适应性。
上述方法都是在Fourier变换的基础上发展起来的,但是Fourier变换存在时间域和频率域的相互制约,无法兼顾时间轴和频率轴的分辨率,并且在处理非线性非平稳信号时效果较差。1998年,HUANG等[15]首次提出希尔伯特-黄变换,这是一种用于处理非线性、非平稳信号的时频分析新方法,该方法由经验模态分解[16]和Hilbert谱分析两部分组成。经验模态分解就是将非平稳信号按频率由高到低分解为一系列固有模态函数,这一系列固有模态分量能反映出原始信号在不同频率上的局部特征。对每个固有模态分量进行Hilbert变换,得到每一个固有模态分量随时间变换的瞬时频率和瞬时幅值,求得振幅-频率-时间的三维谱分布[17]。把所有固有模态分量的Hilbert谱进行综合之后即可求出原始信号的Hilbert谱,以此来得到信号的时频属性。希尔伯特-黄变换很适合处理非线性非平稳信号,在地震资料处理和瞬时谱分析中有着广泛应用。然而经验模态分解存在模态混叠现象。模态混叠主要是指同一个固有模态分量当中出现了不同尺度或频率的信号,或者同一尺度或频率的信号被分解到多个不同的固有模态分量当中[18],严重影响了数据分析的结果。为了克服该问题,学者提出了总体经验模态分解算法[19]。总体经验模态分解方法是一种噪音分析法,即在每次信号分解的过程中对原始信号添加高斯白噪声,该方法能够很好地解决经验模态分解算法在分解过程中出现的端点效应[20]和模态混叠现象。总体经验模态分解方法在原始信号中加入了高斯白噪声,所以分解后的结果很难重构得到原始信号,分解不具备很好的完备性。其分解依赖添加白噪声幅值和集成次数,如果参数选择不合适,不仅不能抑制模态混淆,而且会出现伪分量;且也无法保证分解得到的分量满足固有模态分量的定义条件[21]。总体经验模态分解方法需要的计算量非常大,计算效率较低,不利于实际地震资料的处理。TORRES等[22]在2010年提出完备总体经验模态分解,与总体经验模态分解不同的是,该方法向原始信号中加入了正负成对形式的白噪音,这样重构信号中的残余辅助信号被有效消除,从而简化计算量。完备总体经验模态分解既继承了经验模态分解的正交性、自适应性以及能够处理非平稳信号的特点,又在总体经验模态分解的基础上简化了计算量,几乎可以重构完整的原始信号。
经验小波变换作为一种全新的自适应性算法在信号处理中得到应用。经验小波变换能够更好地分解出原始信号中固有的本征信号,因此其较经验模态分解和总体经验模态分解算法有更高的自适应性。经验小波变换以成熟的小波理论为基础,其数学理论基础非常充分,自身具有较高的计算效率。考虑到经验小波变换是基于经验模态分解的最新自适应算法,本文先介绍了经验模态分解和经验小波变换的基本原理,然后提出基于经验小波变换的瞬时谱分析技术,最后将其应用到致密砂岩气藏的检测中。本文首次将经验小波变换应用到瞬时谱分析技术中检测致密砂岩气藏,得到了较好的效果。
1 基本原理
1.1 经验模态分解
HUANG等[15]人认为,只有固有模态分量的瞬时频率具有物理意义。经验模态分解基于简单的假设,即任何数据都包含不同的简单固有模式。这些振荡模式中的每一种都由固有模态分量表示,具有以下定义:①在整个信号段中,极值的数量和过零的数量必须相等或相差最多一个;②在任何时候,由局部最大值定义的包络的平均值和由局部最小值定义的包络为零。固有模态函数定义的第一个条件类似于静态高斯过程的窄带要求。第二个条件使用局部要求而非全局要求,这使得由对称波形引起的不需要的波动不会出现在瞬时频率中。
固有模态函数的定义表明,数据的内部振动模式由固有模态分量表征。每个固有模态分量只涉及一种振荡模式。振荡也将相对于“局部均值”对称。线性或非线性的固有模态分量可以在简谐分量中具有恒定的幅度和频率,也可以在时间函数中具有可变幅度和频率。经验模态分解通过将多组分信号简化为单组分函数的集合[23],解决了从多组分信号中计算有意义瞬时频率的难题。最终的复杂信号是由固有模态分量的重叠形成的。经验模态分解的目的是获得固有模态分量。通过经验模态分解方法分解的固有模态分量,可以通过筛选过程根据信号本身的相邻极值点之间的延迟来定义和区分。
HUANG等[24]表明,为了获得关于经验模态分解详细而经验性的统计知识,经验模态分解基本上充当了与小波分解相关的二元滤波器组[25],经验模态分解方法将信号分解为固有模态分量的步骤如下:
1)识别时间序列信号X(t)的所有极值点,使用X(t)的所有极大点确定上包络u(t),并用所有的极小点确定下包络v(t),X(t)满足:
v(t)≤X(t)≤u(t)
(1)
然后,上包络线和下包络线的平均曲线m(t)是:
(2)
设h1(t)=X(t)-m(t),那么h1(t)就是固有模态分量。
2)由于过冲和俯冲,包络样条将近似产生一个新的极值,它会影响原始极值点的位置和大小。因此,h1(t)不完全满足固有模态分量条件。为了获得所需的h1(t),让h1(t)代替X(t)。对应于h1(t),上包络线为u1(t),下包络线为v1(t),然后重复这个过程:
(3)
h2(t)=h1(t)-m1(t)
(4)
⋮
(5)
hk(t)=hk-1-mk-1(t)
(6)
重复该过程直到每个hk(t)满足固有模态分量条件。然后,获得第一个固有模态分量C1(t)和信号r1(t)的剩余部分:
C1(t)=hk(t)
(7)
r1(t)=X(t)-C1(t)
(8)
在信号的剩余部分继续使用经验模态分解。分解继续进行,直到信号的剩余部分单调或其值小于预定值。分解后得到的固有模态分量和余量为:
r2(t)=r1(t)-C2(t)
⋮
rn(t)=rn-1(t)-Cn(t)
(9)
X(t)可以表示为固有模态分量和余量之和:
X(t)=C1(t)+C2(t)+…+Cn(t)+rn(t)
(10)
1.2 经验小波变换
经验小波变换的目标是通过构建自适应小波来提取不同的单分量。该方法的步骤如下:
1)将快速Fourier变换应用于信号f(t),从而获得频谱X(w),其中f(t)是离散信号,t={ti}i=1,2,…,M(M表示样本数)。在Fourier频谱中找出最大值M={Mi}1,2,…,N(N表示最大值的数量),并推导它们的相应频率W={Wi}i=1,2,…,N。
2)获得Fourier频谱和边界集的适当分段。将每个段的边界Ωi定义为两个连续最大值的中心:
(11)
式中:Wi和Wi+1为两个频率;边界集是Ω={Ωi}i=1,2,…,N-1。
3)定义一组由一个低通滤波器和基于边界的N-1个带通滤波器组成N个小波滤波器。尺度函数φ1(W)和经验小波ψi(W)的Fourier变换的表达式如下:
(12)
(13)
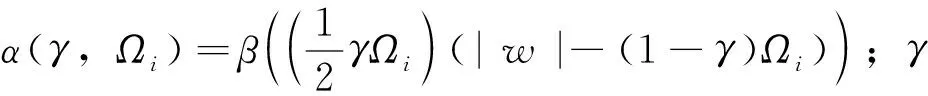
(14)
求取尺度函数和小波函数以提取不同单分量。近似系数由分析信号f(t)的内积与经验尺度函数表示:
(15)
类似地,细节系数是通过经验小波的分析信号f(t)的内积得到的:
(16)
式中:Wf(i,t)表示第t个时间点的第i个滤波器组的细节系数。
怎样将Fourier谱进行分段在经验小波变换中至关重要,其直接关系到对原始信号进行分解后的自适应程度。经验小波变换将原始信号进行不同的分割,比如对某个中心频率的紧支撑部分进行分割。假设断点数目为N,意味着需要N+1个边界。除了起点0和终点σ以外,还需要N-1个边界。为了找到这些边界,首先对信号频谱的局部极大值点进行降序排列(起点0和终点σ包括在内)。假设找到了M个极大值点,下面两种情况将会出现:①M≥N:算法发现了足够的极值点以便于分割原始信号,但只取前N-1个极大值点;②M≤N:信号没有预期的那么多模态,将这M个极值点保留,并添加一些近似值直到极值点达到N个。
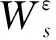
(17)
(18)
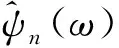
这样原始信号可以通过下面的式子来重构:
(19)
为简单起见,经验小波变换所蕴含的经验模态函数可以定义为:
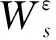
(20)
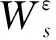
(21)
1.3 基于经验小波变换的瞬时谱分析技术
瞬时谱分析(instantaneous spectral analysis)能够对地震信号进行连续时频分析,观察任一时间点处振幅变化情况及频率分布。
基于经验小波变换的瞬时谱分析技术实现步骤为:①利用经验小波变换将某一单道地震信号分解成按频率高低分布的固有模态分量;②求取各个固有模态分量中的瞬时频率分布;③将各个固有模态分量的频率分布依据时间叠加得到该地震道的时频剖面;④依次选取二维地震记录中每个单道记录,重复进行步骤①~③;⑤从各时频剖面中提取特定频率分量,根据对应的地震道位置依次叠加,最终得到特定频率的瞬时谱。
评判瞬时谱分析剖面时遵循以下原则:①时频分布沿着频率的振幅叠加值与信号的瞬时振幅值近似相等;②时频分布沿着时间的振幅叠加值与信号的瞬时频率值近似相等;③地震剖面上明显的构造,在瞬时谱剖面上也必须表现出来;④地震剖面上明显的构造异常旁瓣,在瞬时谱剖面上不能单独出现;⑤一个单独的同相轴在瞬时谱剖面上是连续的。
2 合成数据
为验证本文所提方法的有效性,现构造一个典型的非平稳信号,分别利用经验小波变换和其他时频分析方法对其进行对比,如短时Fourier变换,S变换,经验模态分解。
该信号具体形态(见图1)为20 Hz背景余弦波,在300 ms处叠加100 Hz Morlet子波,在1 070 ms和1 100 ms处叠加了两个30 Hz Richer子波。在1 300~1 700 ms之间,信号具有3种不同的频率组分:7,30和40 Hz,其中7 Hz的频率是不连续的,并且包含少于一个周期的部分,出现在1.37,1.51和1.65 s。该信号具有显著特征,为典型的非平稳信号,适合用于检验时频分析方法的优劣。
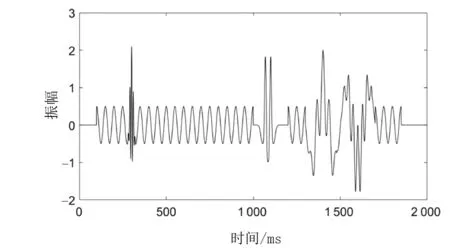
图1 测试信号Fig.1 Test signal
2.1 信号分解对比
经验模态分解将原始信号分解成了7个固有模态分量(见图2(a)),在300 ms处信号频率大幅突变,导致固有模态分量1(IMF1)中虽提取出了Morlet子波的高频成分,但混杂了20 Hz背景余弦波、1 100 ms处的Ricker子波等低频成分。同样,固有模态分量2(IMF2)、固有模态分量3(IMF3)、固有模态分量4(IMF4)中均是各种组分的高频部分和低频部分混杂在同一固有模态分量中,难以识别出信号包含的具体频率组分,使信号分析复杂化,这属于典型的模态混叠现象。图2(b)是经验小波变换分解原始信号的结果,IMF1表示1 300~1 700 ms之间的低频组分(7 Hz)。IMF2中包含20 Hz背景余弦波、1 300~1 700 ms处低频组分及1 070 ms和1 100 ms处两个Ricker子波。而IMF4仅提取了300 ms处的Morlet子波,没有其他组分混杂。IMF3则为少量Morlet子波剩余组分和Ricker子波剩余组分。经验小波变换分解效果明显优于经验模态分解分解效果。
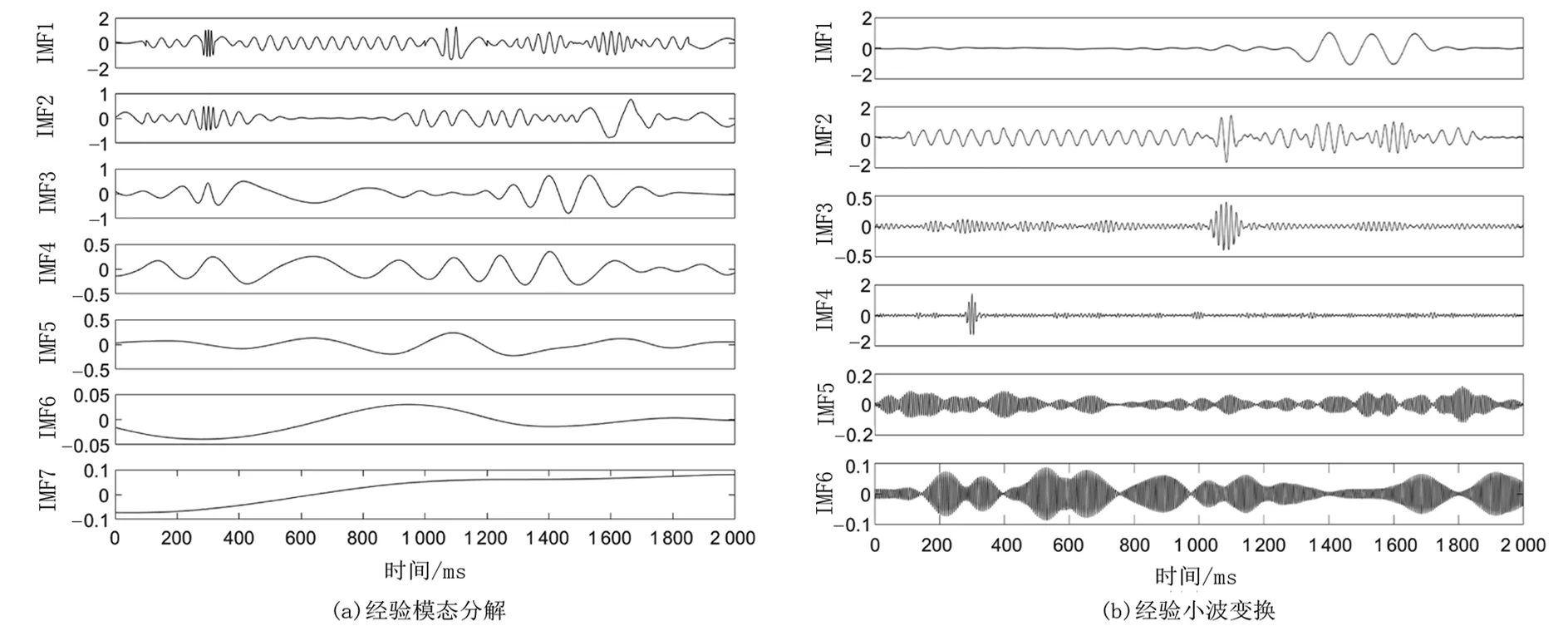
注:IMF为固有模态分量。图2 不同方法的信号分解结果对比Fig.2 Comparison of signal decomposition results of different methods
2.2 时频谱对比
图3(a)是经过128ms时间窗的短时Fourier变换得到的时频谱,30 Hz背景余弦波、300 ms处的100 Hz Morlet子波、1 300~1 700 ms处的低频部分的轮廓已凸显出来,但时频分辨率过低,能量显示较为分散,只能观察到各频率组分的大致分布情况,受Heisenberg测不准原理制约,缺乏实际研究价值。
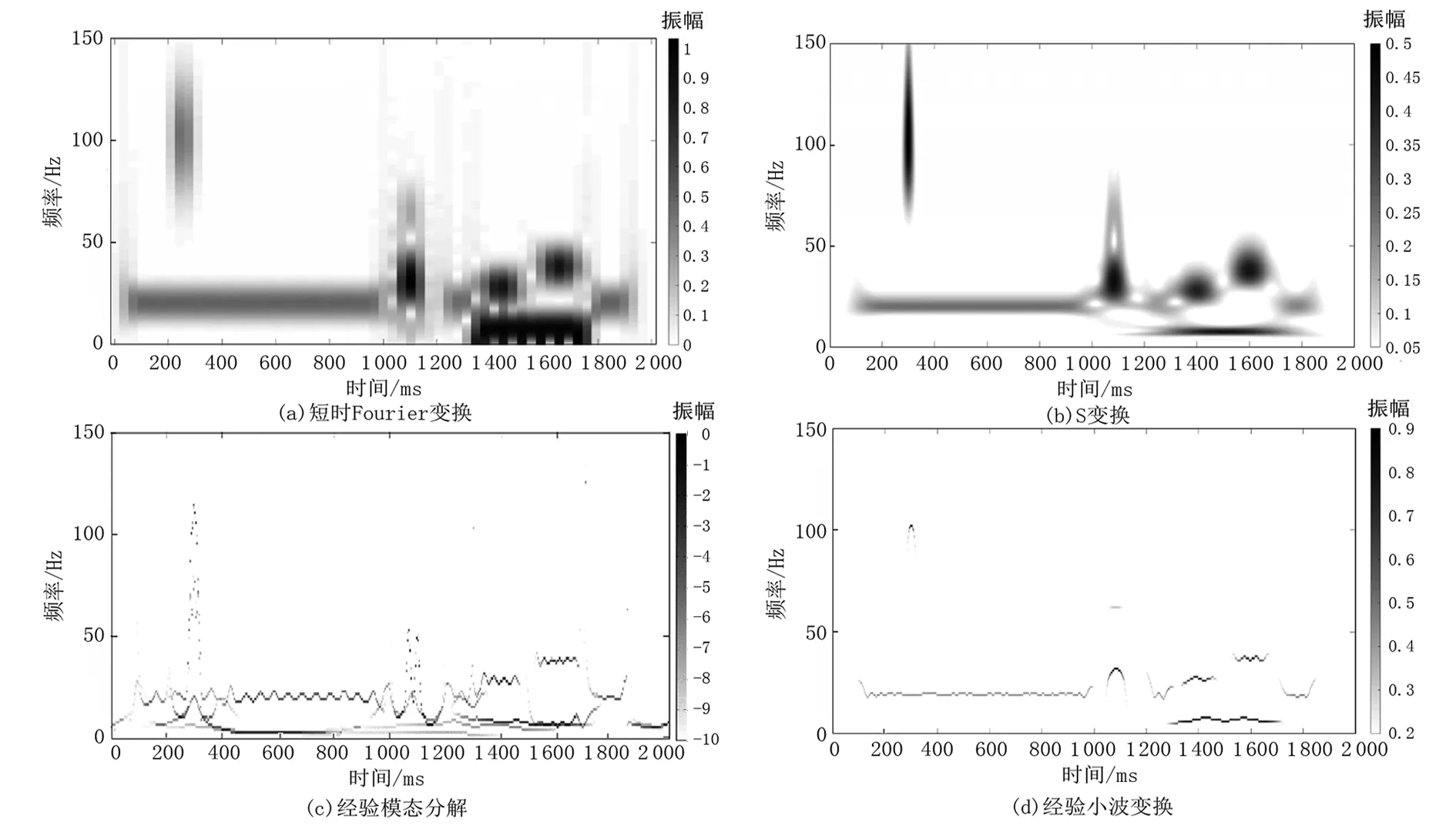
图3 不同方法处理原始信号得到的时频谱对比Fig.3 Comparison of time spectrum obtained by processing raw signals with different methods
图3(b)是通过S变换得到的时频谱,在300 ms处的频率分辨率很低,无法识别出100 Hz Morlet子波,1 300~1 700 ms处的时频分辨率较短时Fourier变换相比有明显提升,能量显示更为集中。
图3(c)显示通过经验模态分解得到的瞬时谱,图中30 Hz背景余弦波,1 300~1 700 ms处低频组分以及1 100 ms附近的两个Ricker子波均清晰可见,时频分辨率较前两种方法有质的飞跃。在信号两端可见明显的发散现象,属于典型的端点效应,导致200~1 800 ms间有大量低频成分混杂,特别是在300 ms处100 Hz Morlet子波部分,其上下均有能量泄露,信号失真十分严重。
经验小波变换处理后的瞬时谱(见图3(d))首次将1 300~1 700 ms处的7 Hz频率特征准确地刻画出来。30 Hz背景余弦波、Ricker子波以及1 300~1 700 ms处其他频率组分均以最高时频分辨率呈现出来,且300 ms处高频突变部分标识准确,能量非常集中,信号两端未出现端点效应。对比上述4种时频分析方法处理结果,可以发现经验小波变换明显优于其他3种方法。
3 实际地震资料处理
为了验证本文方法在含气检测中的有效性,针对中国某地区的实际资料进行瞬时谱分析。该区储集层物性总体较差,属致密-超致密砂岩区块。该区天然气的富集、产出和高产与裂缝的发育程度关系极为密切。考虑到裂缝的存在以及天然气的影响使地震波速度明显降低,造成物性参数转换上具有不同程度的突变特征,因此该地区的地震资料具有非线性非平稳的特性,适合利用本文的经验小波变换对该区储集层的含气特征进行研究。
取实际地震资料的部分叠后剖面(1 550至2 000道中1 500~2 000 ms,见图4)进行应用。地震资料经过瞬时谱分析技术处理后常出现含气区下方振幅异常的低频阴影现象,低频阴影现象是含气检测的主要依据。用基于经验小波变换的瞬时谱分析技术处理地震资料,提取3~7 Hz低频、13~17 Hz中频以及23~27 Hz高频的瞬时谱剖面,结果如图5所示。图5(a)3~7 Hz低频瞬时谱剖面,在含气储层中信号能量迅速衰减,在其下方(红色椭圆内)存在强大的能量分布,出现低频阴影现象;图5(c)23~27 Hz高频瞬时谱剖面,当频率增大时,含气储层中能量增大,其下方的低频阴影现象消失。结合低频和高频瞬时谱剖面,对比能量分布差异可以很好地确定含气区域。
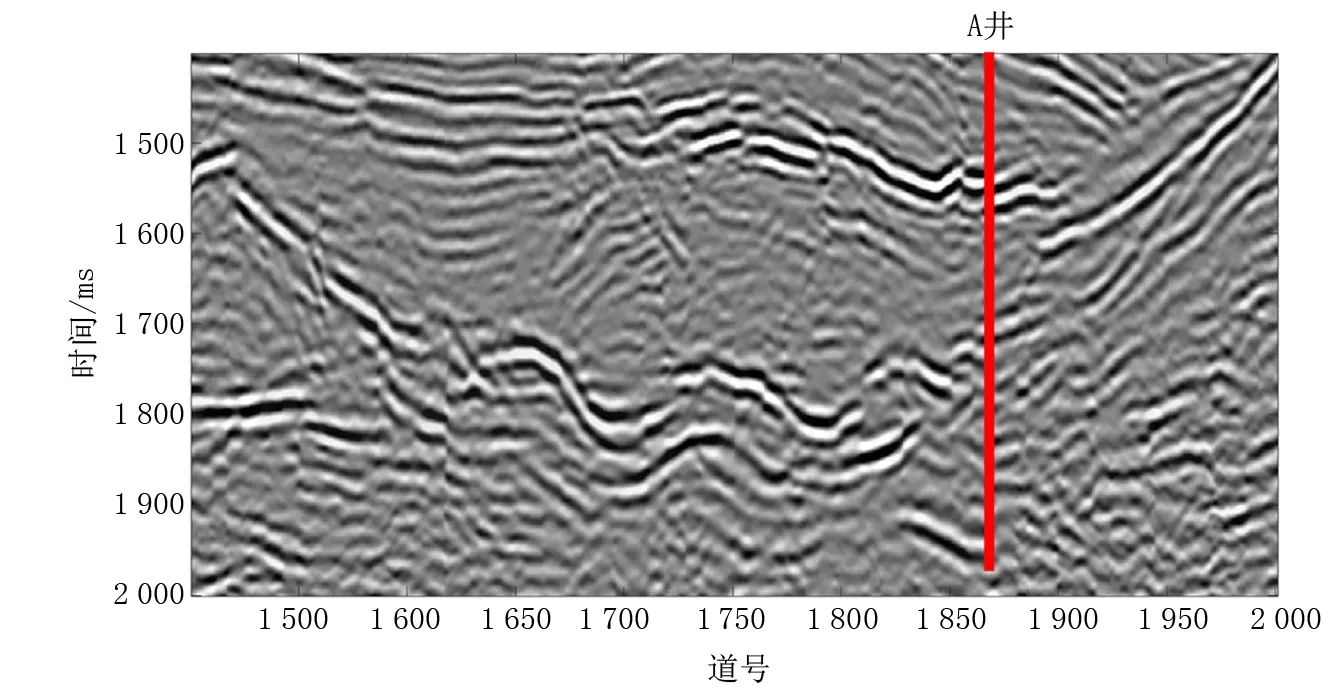
图4 中国某地区实际资料叠后地震剖面Fig.4 Post-stack seismic profile of actual data in a region of China
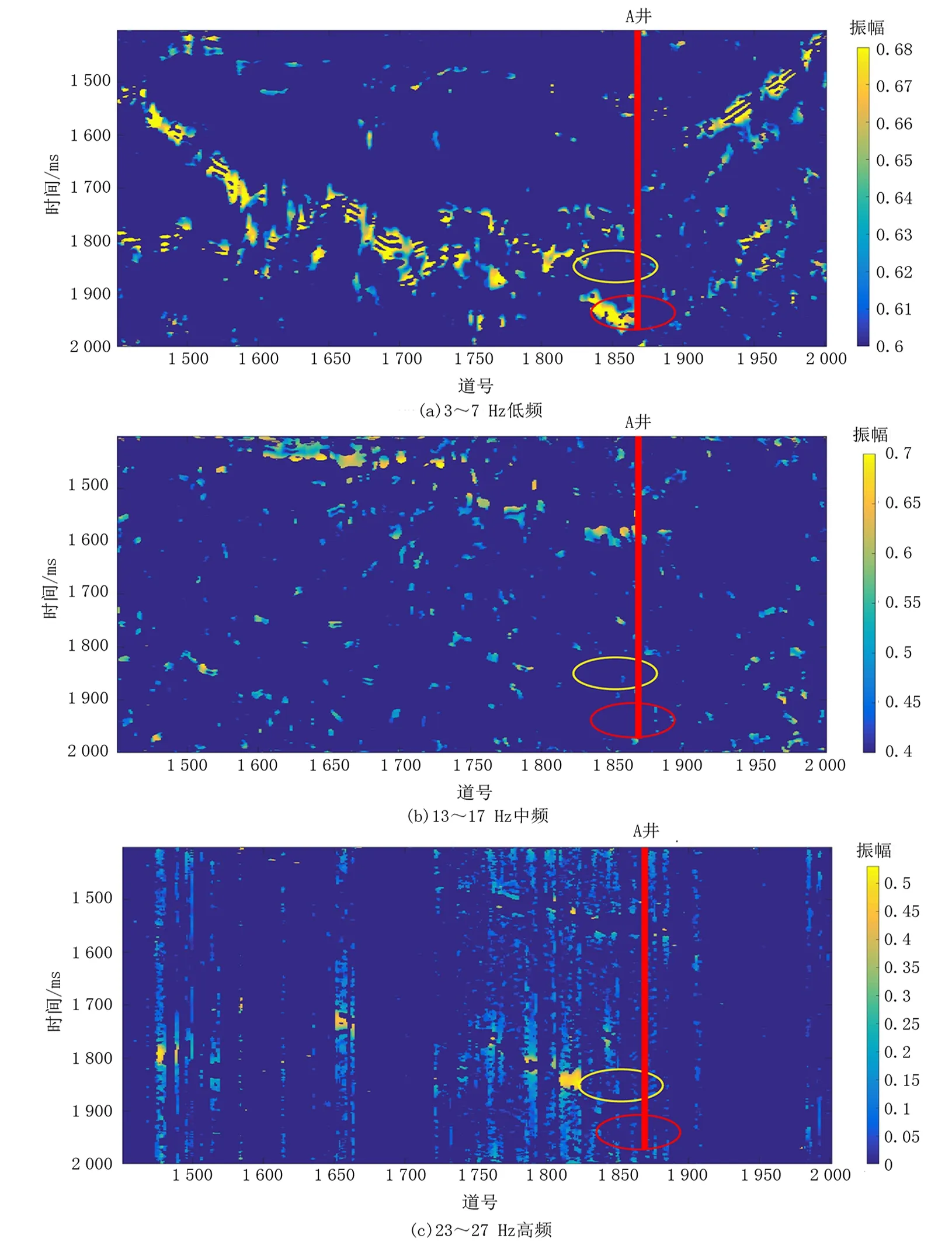
注:黄色椭圆表示储层位置,红色椭圆表示低频阴影处,红色竖线表示A井所在位置。图5 基于经验小波变换的瞬时谱分析技术处理得到的瞬时谱剖面Fig.5 Instantaneous spectrum section processed by instantaneous spectrum analysis technique based on empirical wavelet transform
4 结束语
经验小波变换是一种全新的自适应分析算法,具有很高的自适应性,其时频分析解决了模态混叠问题,能够有效地去除线性噪音,也不易丢失数据。本文将经验小波变换应用到瞬时谱分析技术中,得到了一种新的瞬时谱分析技术,与基于传统时频分析方法的瞬时谱分析技术相比解决了Heisenberg测不准原理的制约等难题,具有更高的时间和频率分辨率。本文将基于经验小波变换的瞬时谱分析技术应用于实际致密砂岩气藏资料的含气检测中,一维地震道分析效果优于其他方法,二维地震道分析中低频阴影更加明显,低频与高频的瞬时谱剖面结合能够更好地反映地层细节,更有效地识别致密砂岩气藏的含气岩层。

