一个三元轮换对称不等式及其推广的证明①
2023-09-21 05:25叶瑞松
数学通报 2023年6期
叶瑞松
(汕头大学数学系 5150630)
由于对称不等式形式优美,结论耐人寻味,其论证方法和论证过程更有各种便捷巧妙的技巧,对称不等式相关的研究是一个很有生命力的研究领域,可以说是集中体现数学之美的一类研究.[1-5]文[1]证明了三元对称不等式的定理1.
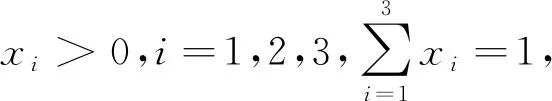
文[1]用“微分法”给出了定理1的证明,证明过程繁琐,难于理解.后来,文[2]和[3]分别用初等方法给出比较简单的证明.文[4]利用数学归纳法将定理1进一步推广到更一般的形式,即下面的定理2.
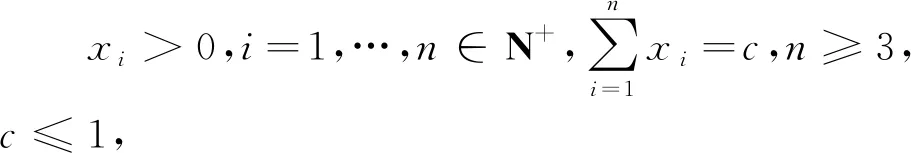
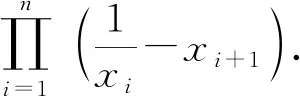

证明采用基本不等式进行证明.
由算术-几何平均不等式得到

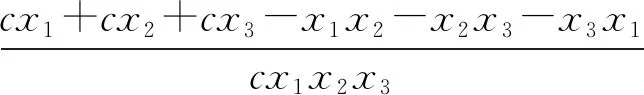
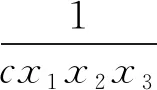
证明完毕.
我们将定理3进一步推广到多元情况,得到定理4.
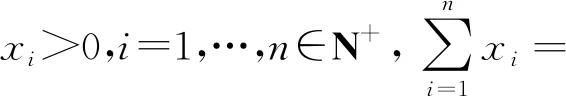
为了证明定理4,我们先给出引理1,然后用数学归纳法证明引理2的结论,再利用定理2,便可以得到本文定理4的证明.本文主要结果引理2和定理4来自引理1的启发,引理1可以由函数凸性得到,在文献[6]中有其简洁的证明.由于引理1在本文中所起的作用,我们将其简短的证明也提供出来,供欣赏参考.
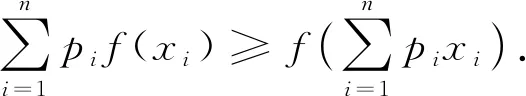
证明由于b≥max{c,d},a+b=c+d,
所以b>a,c>a,d>a且
由f(x)的凸性得到
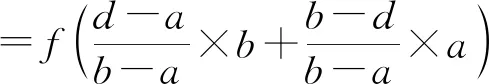
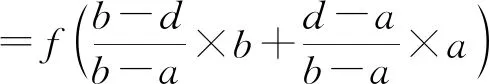
将上述两个式子相加,得到
f(a)+f(b)≥f(c)+f(d).
引理2如果f(x)是(0,∞)上的凸函数,0 所以,n=2时,引理2结论成立. 假设n=k,k∈N+时,下面不等式成立: 则当n=k+1时, 由于不等式具有轮换对称性,不妨假设xk+1≤min{x1,…,xk},则 所以由引理1知道 从而 所以当n=k+1时,引理结论成立. 由数学归纳法知道,引理结论对任何正整数均成立.证明完毕. 去掉对数,由定理2的结论,得到 证明完毕.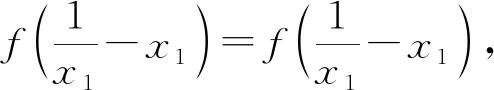
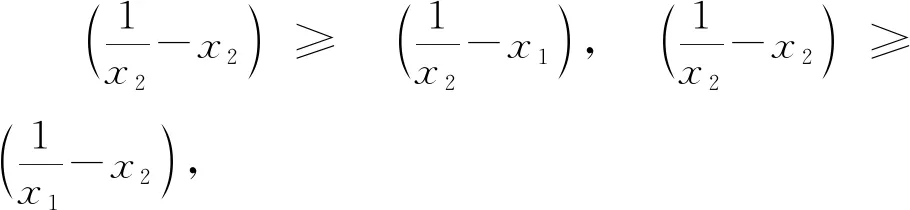
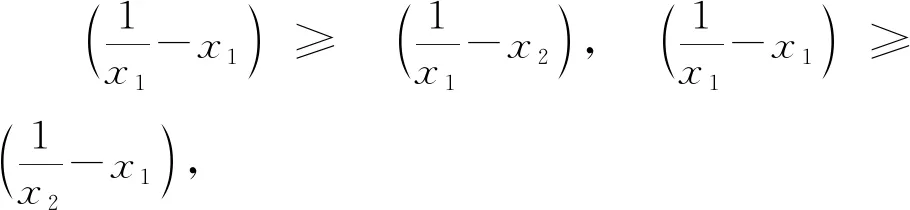
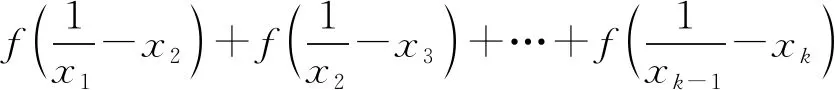
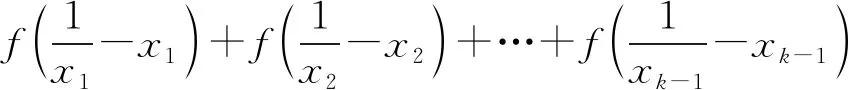
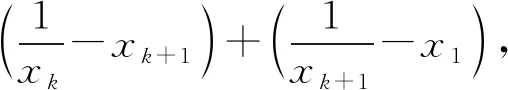
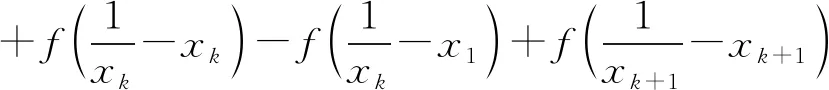
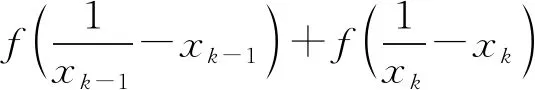
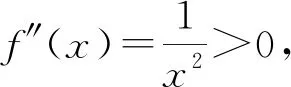
猜你喜欢
地震研究(2023年3期)2023-07-21
中学生数理化·八年级物理人教版(2021年11期)2021-12-06
中学生数理化(高中版.高二数学)(2021年4期)2021-07-20
系统管理学报(2018年3期)2018-08-13
系统管理学报(2018年2期)2018-08-13
中学物理·高中(2016年12期)2017-04-22
试题与研究·教学论坛(2017年3期)2017-02-17
延边大学学报(自然科学版)(2015年3期)2016-01-08

