以直觉锁定特征 借目标优化运算①——圆锥曲线中定点、定值问题的教学思考

唐 毅

(江苏省镇江中学 212000)

1 问题提出

在解析几何中,圆锥曲线是核心内容之一. 我们通常采用“先用几何眼光观察与思考,再用坐标法解决”的策略,用数形结合的思想研究这些曲线. 然而,在平时的教学中,我们发现,许多学生在解决解析几何问题时,常规的操作水到渠成,但一旦到达化简、求值的关键运算步骤时,就容易失去方向,导致功亏一篑. 这表明,在式子变形等计算训练方面,现在的教学有着一定缺陷,在日常教学中,教师总是认为变形是繁琐而没有价值的训练,学生也认为只要认真对待就能够算出结果,从而忽视了运算中的观察和简化,这才造成了运算素养及解题能力的弱化. 圆锥曲线题目通常有较大的运算量,因此运算的技巧,例如巧妙的利用式子变形,能够起到非常重要的作用. 在圆锥曲线教学中,我们需要注意收集圆锥曲线的典型例题,挖掘其中丰富多彩的性质,并与学生进行分析,引导学生对几何问题进行代数化简变形. 解析几何难,难在运算;运算难,难在关键步骤的处理;关键步骤难,难在解题方向不明,特别是圆锥曲线中与定点、定值有关的问题. 这些问题体现了运动变化的思想,同时也蕴含着运动变化过程中保持的某种“规律性”或“不变性”.

下面我们以一道有关定点定值问题的高考题为例,探索如何获取结论,如何利用结论规划解题路径,如何优化运算,提升问题解决的效率,在分析这道高考题的过程中,我们可以看到式子变形能力起到的重要作用.

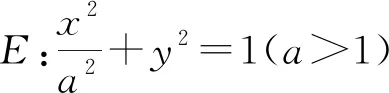
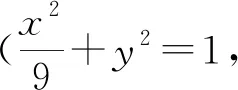
(2)证明:直线CD过定点．(本文重点讨论)

2 探求性质

2.1 精细作图 明晰运算对象

几何引领代数,运算印证几何．作出图形、分析图形间关系是深刻理解题意,挖掘问题本质,寻求解题突破口的必经之路．按题目要求准确反映图形特征:如图1,选取点P的几个不同位置而形成的直线即可大致发现直线CD恒过x轴上的某定点,所以在计算时关键是计算出直线CD与x轴交点的横坐标．

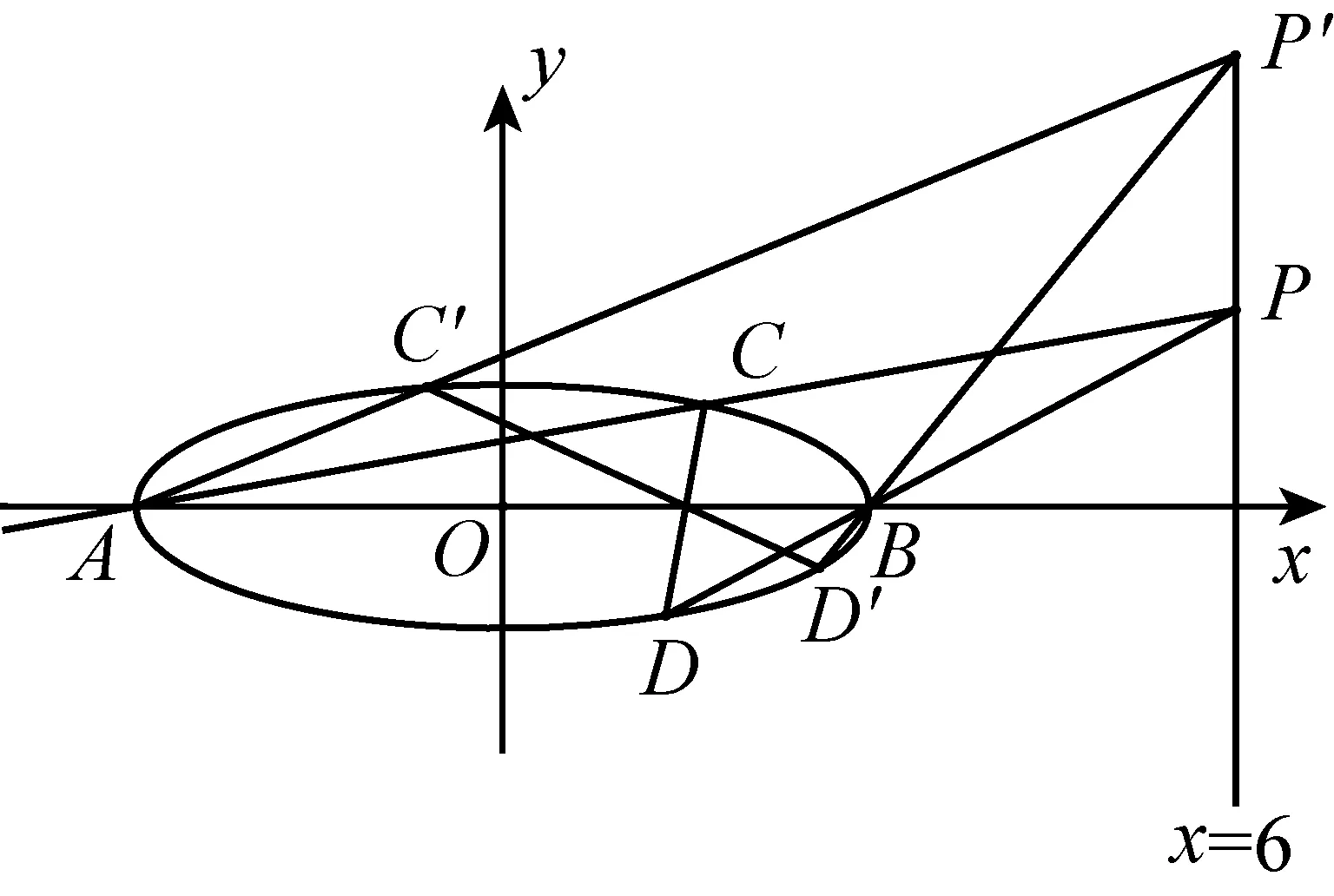
图1

2.2 特殊转化 探索运算思路

圆锥曲线背景下运动或不变性必然会导致存在复杂的关于字母符号的化简,如果课堂实践中先引导学生进行特殊情况下的转化,就能为一般化情况的探索指明方向．

直觉上感知如果直线CD过定点,必在x轴上．可以通过对称的手段感知．关于对称,由椭圆图形以及点P轨迹的轴对称性,在某情形成立之下,作出此类情况关于x轴的镜像必定也符合题意,如图2,说明点在x轴上的必然性．

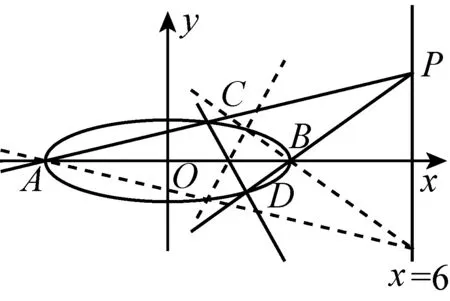
图2

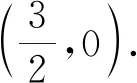
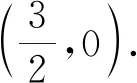
如果尚未获取点的位置信息,那么就选取两个特殊位置,如取yP=0,yP=1,两种状态的CD交点必为定点．

如果点P的纵坐标趋向于无穷大,那么直线PA与PB将趋近于与y轴平行,C,D两点无限逼近A,B,如图3,直线CD的极端情形即为x轴,同样也说明了定点的位置．

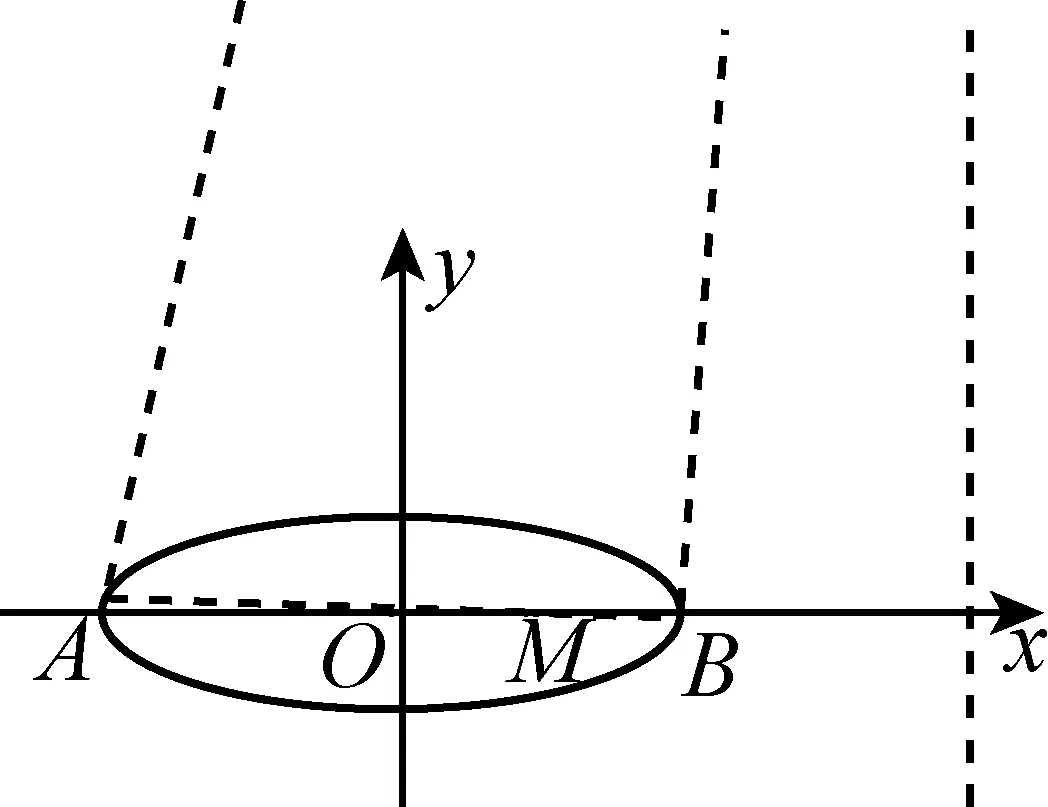
图3

通过特殊情形判断分析出了定点位置后,接着就是需要通过代数运算来证明,在这一过程中,如果学生有良好的数学式子变形能力,结果并不难得到.但如果式子变形能力差,计算将变得非常复杂,容易导致运算错误.

3 优化运算

3.1 化探求为验证

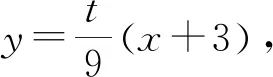
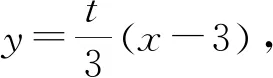
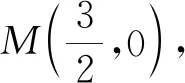
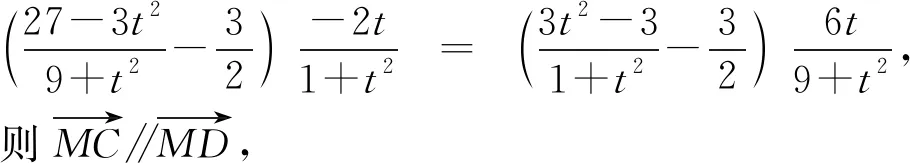
从这里就可以看出,如果不具备良好的式子变形能力,而是通过求根公式来求解x1,x2,计算就会复杂很多,甚至会带来不必要的运算错误.若是通过图形认识到直线PA与椭圆的公共点为点P和点A,从而可知对应的关于x的一元方程的两个根就是点P和点A的横坐标,从而引导快速运算.

3.2 化运算为表述

同上解,得到

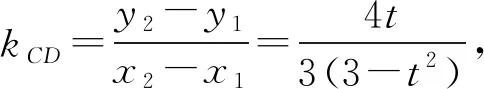
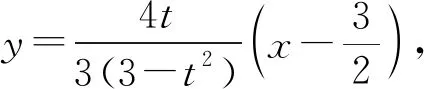
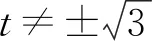
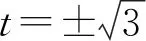
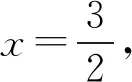
3.3 化解根为构造

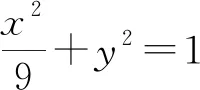
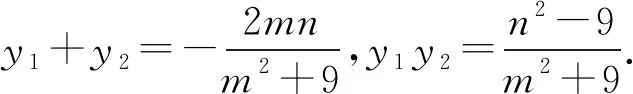
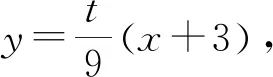
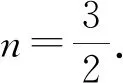
评注:在这个解法中,式子变形起了非常重要的作用,特别是将x+3和x-3看成整体,然后再进行式子变形,使得求解变得简洁很多.如未进行这样的优化计算,而是机械地代入方程进行繁杂的计算,在具有这么多未知量的情况下,想得到准确结果,绝非易事.

因此,教师在具体优化计算的教学过程中,需要帮助学生回顾几何特征,从寻找运算思路,到边化简变形边发现核心计算难点,再到突破难点反思运算过程,学生就一道题不断经历:几何问题——代数方向——运算策略——化简难点——解决问题——反思比较的过程,学生的运算素养必然不断获得提升.

4 结束语

与圆锥曲线相关的题目浩如烟海,现在的教学依然有着很大缺陷,仅仅依靠让学生做大量的练习是不能让他们真正理解圆锥曲线的特征并掌握运算规律的.我们要善于利用典型的问题,结合其结论特征,在运算过程中,仔细观察每一步式子的结构,进行合理有效的式子变形,优化运算,提高运算准确性.因此,在例题化归、变式训练、课后作业中,我们需要坚持在更换背景、原命题逆命题互换、化简策略变化上多思考,多实践,加大计算分析的力度,给学生提供从不同角度感悟解析几何思想与方法的机会,不断提升运算素养.同时,我们也需要更加强调运算能力的重要性,让学生意识到只有通过强化运算能力,才能真正掌握解题的方法和技巧,从而在更高的层次上理解圆锥曲线和其他解析几何的知识.