参与一次调频储能型风电场的交流外送振荡特性分析

杨 滢，杨晓雷，项中明，黄金波，张红颖，郝丽丽

（1.国网浙江省电力有限公司，浙江杭州 310007；2.国网浙江省嘉兴供电公司，浙江嘉兴 314000；3.中国电力科学研究院有限公司，江苏南京 210009；4.南京工业大学电气工程与控制科学学院，江苏南京 211816）

0 引言

风电功率具有间歇性与波动性，其迅猛发展对电网的稳定运行带来较大的影响[1-3]。为提高含风电系统的频率稳定性，文献[4]为风电增加了惯量控制和下垂控制，有效提高了系统等效惯量，但风电机组捕获的机械功率恒定，使其无法持续参与系统的一次调频。文献[5-7]采用超速减载降低风电机组出力，预留备用参与系统的一次调频。文献[8]通过控制桨距角来降低机组出力，预留备用容量，在频率变化时参与系统调频，但桨距角调整速度慢，且其频繁动作增加设备损坏风险和维护成本。储能系统响应速度快、短时功率吞吐能力强，具有双向调节和精确跟踪的能力，因而在风电渗透率不断增加的情况下，储能独立[9-14]或与风机协调[15-16]进行一次调频的方向逐渐引起学者关注。文献[9]基于理论设计了储能的频率控制方法。文献[10]利用储能系统为风电场补偿一定的虚拟惯量。文献[11]通过配置超级电容储能参与双馈感应发电机（Doubly-Fed Induction Generator，DFIG）的惯量支撑和一次调频，提高系统的频率稳定性。文献[12]依次启动储能系统、桨距角控制或传统电源参与系统调频，但没有利用各个调频方式的互补特性。文献[13]储能系统通过下垂控制与设置死区来参与系统频率调节，但储能与风机控制相互独立，未考虑两者的协调配合。随着风电和储能接入比例的提高，其共同进行频率调整的需求更加迫切，需要研究其接入对系统振荡特性的影响。

通常采用特征值法与时域仿真相结合的方法分析风电并网系统稳定性的影响因素。文献[17]采用特征值法分析了风速与双馈风电场外送线路串补度对系统稳定性的影响。文献[18]基于特征值灵敏度分析方法和时域仿真法，研究了风速、串补度、转子侧变流器和风机台数对系统稳定性的影响。文献[19]基于特征值法和时域仿真法，研究了锁相环（Phase-Locked Loop，PLL）参数和风电场接入电网强度对系统振荡特性的影响。对风电并网系统振荡特性影响的研究中，较少考虑风机自身参与调频及储能系统接入下系统稳定性的变化情况。

基于以上分析，本文采用DFIG 设置超速减载控制、惯量控制及下垂控制相结合的调频方法来提高系统的频率稳定性。为进一步增强系统的频率响应能力，在风电场出口汇流母线处配置了集中式储能参与系统的一次调频，并研究了风-储调频控制策略。采用特征值法分析了风电机组及储能系统参数设置和系统短路比对系统振荡特性的影响，并对比分析了不同的风-储调频控制策略对系统稳定性的影响。

1 DFIG交流并网模型

DFIG 交流并网模型如图1 所示。DFIG 由风机、感应发电机、网侧变流器（Grid Side Converter，GSC）及转子侧变流器（Rotor Side Converter，RSC）组成。线路电阻RL、线路感抗XL、线路容抗XC组成输电线路。其中，Xtg为GSC 侧电抗；Crowbar 为撬棒电路，用以在故障发生时保护转子侧变流器。

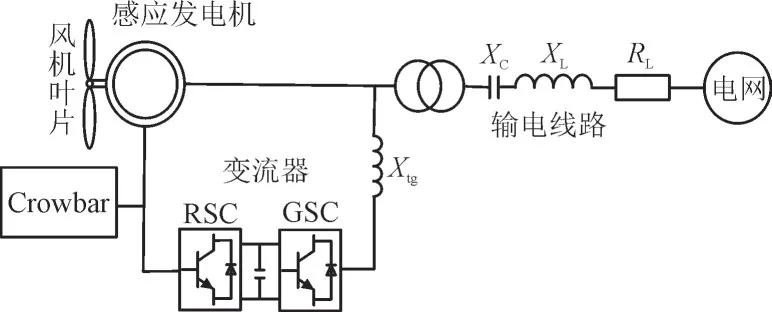
图1 DFIG交流并网模型Fig.1 DFIG AC grid-connected model

1.1 风电机组传动系统模型

传动系统二质量块模型广泛用于风电并网电力系统的稳定性分析[20]，各参数标幺后模型如式（1）所示。

式中：Tm为风电机组风机侧的机械转矩；Te为风电机组发电机侧的电磁转矩；D为风机轴系阻尼系数；K为风机轴系刚度系数；ωr为风机转子转速；ωg为发电机转子转速；Hr为风机惯性时间常数；Hg为感应发电机惯性时间常数；ωb为系统角速度的基值；θs为轴系扭转角；t为时间。

1.2 感应发电机模型

以发电机额定功率进行标幺后，同步旋转坐标系下感应发电机电压的状态方程如式（2）所示。

式中：uds，uqs分别为定子d轴、q轴电压分量；ids，iqs分别为定子d轴、q轴电流分量；ψds，ψqs分别为定子d轴、q轴磁链分量；udr，uqr分别为转子d轴、q轴电压分量；idr，iqr分别为转子d轴、q轴电流分量；ψdr，ψqr分别为转子d轴、q轴磁链分量；ωs为同步角速度；s为转差率；Rs，Rr分别为定子、转子电阻。

磁链方程如式（3）所示。

式中：Xs为定子漏抗；Xr为转子漏抗；Xm为励磁绕组电抗。

1.3 变流器模型

网侧变流器可以起到保持直流母线电压稳定的作用，可忽略其对系统振荡特性的影响[16]。因此，本文仅计及RSC 对系统振荡特性的影响，设置中间变量x1，x2，x3，x4，由中间变量将控制流程线性化，得到RSC 的状态方程如式（4）所示。

感应发电机转子侧电压方程如式（5）所示。

式中：Ps，Ps_ref，Qs，Qs_ref分别为感应发电机定子有功功率及无功功率的实际值和参考值；Kp1，Kp2，Kp3，Kp4和Ki1，Ki2，Ki3，Ki4为转子侧PI 控制器比例参数和积分参数；转子漏抗与励磁绕组电抗之和Xrr=Xr+Xm。

1.4 调频控制模型

采用超速减载控制、惯量控制及下垂控制相结合的控制方法[21]，使风电机组参与系统的频率调节，具体控制结构如图2 所示。其中，d为减载比，P*s_ref为风电机组参与调频后感应发电机定子有功功率的参考值，vw为风速，fsys为电网实测频率，fN为基准频率，Δf为fsys和fN间的频率偏差，Kd为惯量控制系数，Kp为下垂控制系数，ΔP1和ΔP2分别为经过惯量和下垂控制得到的感应发电机有功输出功率参考值；d/dt为关于时间的微分环节。

根据空气动力学原理，在某一固定风速下，风机减载运行时的机械功率如式（6）所示。

式中：Pm为风机输出机械功率；Rw为叶片长度，也称为风轮半径；λ为叶尖速比；β为桨距角；ρ为空气密度；Cp为风能利用系数。

为风电机组加入惯量和下垂控制，使其获得类似于传统机组的惯量支撑及调频性能。通过设置惯量控制可以使风电机组具有一定的虚拟惯量，其大小由频率变化量的导数和惯量控制系数Kd来确定，Kd通常与风电机组的额定功率成正比。通过设置下垂控制使风电机组具有与同步发电机类似的频率-功率调节特性[5]，在动态过程中，系统收到的风电机组的有功支持由下垂控制系数Kp决定。将电网实测频率fsys与基准频率fN的偏差Δf作为输入信号，经计算得到功率参考值ΔP1和ΔP2，将ΔP1和ΔP2代入风电机组有功功率参考值的计算环节，得到参与一次调频风电机组输入到转子侧变流器的有功功率参考值P*s_ref。

加入惯量控制及下垂控制后，转子侧变流器的状态方程如式（7）所示。

此时转子侧电压方程如式（8）所示。

1.5 交流输电线路模型

在dq坐标系下交流输电线路的动态模型如式（9）所示。

式中：id，iq分别为输电线路电流d轴、q轴分量；ud，uq分别为无穷大系统电压的d轴、q轴分量；ugd，ugq分别为风电场汇流母线电压的d轴、q轴分量；ucd，ucq分别为输电线路串联补偿电容两端电压的d轴、q轴分量。

2 储能型风电场系统建模

2.1 储能系统模型

蓄电池储能具有充放电速度快、效率高、对地理条件要求低等优点，受到较多关注[22-23]。储能的调频控制模块以功率参考值P*ref为输入，通过双向DC/AC 变流器控制储能与汇流母线之间的能量交换，从而实现储能系统的频率控制，变流器采用空间矢量脉宽调制（Space Vector Pulse Width Modulation，SVPWM）控制框图如图3 所示。

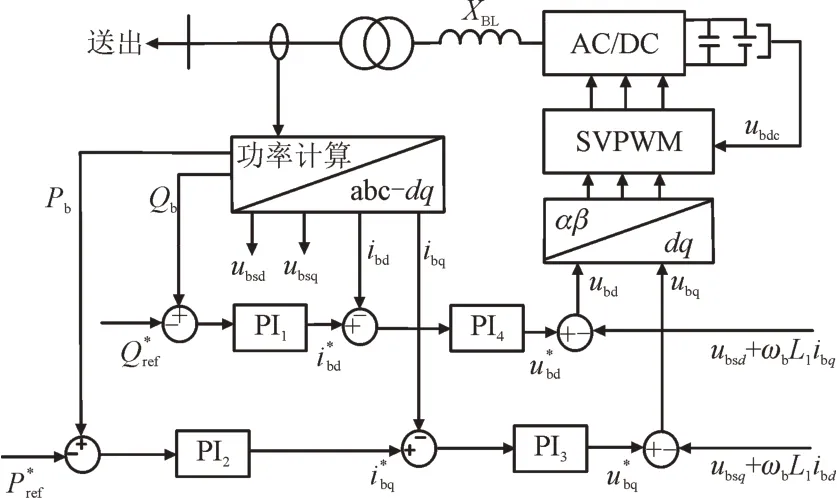
图3 储能系统调频控制框图Fig.3 Frequency regulation diagram of energy storage system

其中，PI1—PI4分别为储能调频控制的比例积分控制器，ibd和ibq分别为储能向汇流母线注入电流实际值的d，q轴分量，i*bd和i*bq分别为储能向汇流母线注入电流参考值的d，q轴分量，ubd和ubq分别为储能变流器交流侧输出电压的d，q轴分量，ubsd和ubsq分别为储能前馈电网电压的d，q轴分量，XBL为储能变流器侧电感，Pb和Qb分别为储能注入汇流母线的有功、无功功率的实测值，P*ref和Q*ref分别为储能注入汇流母线的有功、无功功率的参考值。其模型如式（10）所示。

式中：Kbp1，Kbi1，Kbp2，Kbi2，Kbp3，Kbi3，Kbp4和Kbi4分别为储能系统PI1—PI4控制器的参数。

2.2 风-储独立调频控制

风-储独立控制框图如图4 所示。其中，Pw和Qw分别为风电场流入汇流母线的有功功率和无功功率；Pg和Qg分别为从汇流母线送出的有功功率和无功功率。在风电场出口汇流母线处并联储能，共同向系统供电，风电机组和储能系统各自独立响应系统频率偏差和变化率，调节自身出力大小，实现调频控制。风电机组转子侧变流器采用脉宽调制（Pulse Width Modulation，PWM）调制波形。

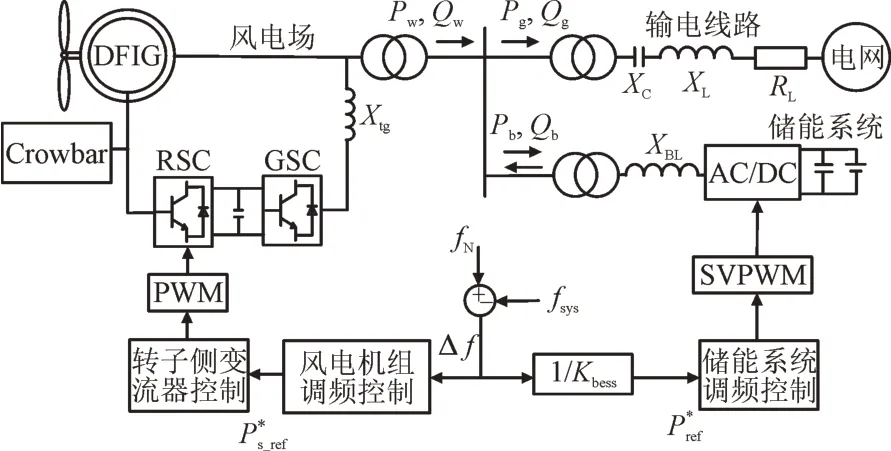
图4 风-储独立控制框图Fig.4 Wind-storage independent control diagram

储能系统调频功率以电网实测频率和额定频率的偏差作为控制信号，经下垂系数Kbess计算得到储能系统的调频功率参考值P*ref，将P*ref作为储能系统调频控制的输入信号，储能调频控制模块如2.1节所示。其中，XBL为储能侧接入电抗。

2.3 风-储协同调频控制

为充分利用风电的调频备用容量，减少储能的频繁启动[24-26]，建立风-储协同调频控制，如图5 所示。当系统频率偏差超过死区fd时，开关置于位置1，储能有功参考值跟随风机调频功率参考值增量而变化，Kb为其比例系数；当系统频率偏差小于死区fd时，开关置于位置2，此时储能功率参考值为0，储能系统不参与系统频率调节，调频功率全部由风机承担。该策略不仅通过储能提高了风电场对电网频率的支撑能力，也起到充分利用风机的减载备用容量，避免储能系统频繁充放电，延长储能系统使用寿命的作用。

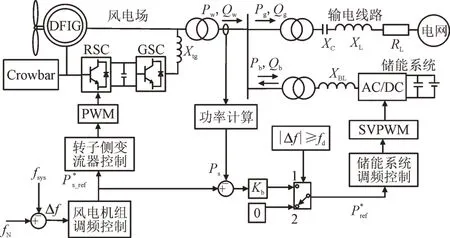
图5 风-储协同控制框图Fig.5 Wind-storage coordinated control diagram

3 储能型风电场交流外送系统振荡特性分析

构建如图4 所示风-储独立控制交流外送系统，变流器侧和储能网侧电感分别取0.52 p.u.，0.13 p.u.，储能参数Kbp1，Kbi1，Kbp2，Kbi2，Kbp3，Kbi3，Kbp4和Kbi4分别取1，100，1，100，1，1，1，1。其中，设双馈风电场由140 台1.5 MW 的DFIG 等值成单台容量为210 MW的风电机组，风机减载比设为10%，储能容量为0.2倍风电场装机容量。特征根分析结果显示系统存在7 组振荡模式：λ1,2，λ3,4，λ5,6，λ7,8，λ9,10，λ11,12，λ13,14，特征值如表1 所示。

3.1 转子侧变流器电流内环控制参数的影响

基于1.4 节的风电机组参与一次调频控制方法，研究转子侧变流器电流内环控制参数Kp2和Ki2对系统振荡特性的影响。对不同Kp2，Ki2下的特征值结果进行分析，发现振荡模式λ5，6的阻尼比始终最小。当固定Ki2，增大Kp2时，特征值实部变大，系统稳定性降低；固定Kp2，增大Ki2时，特征值实部变大，但在相同的增幅下，Ki2所引起的特征值实部变化较Kp2小。可见，Kp2和Ki2增大均不利于系统的稳定，且系统特征值对Kp2的灵敏度较Ki2更大。

不同Kp2，Ki2下的主导振荡模式的振荡频率如图6 所示。

从图6 可知，固定Ki2，增大Kp2时，系统振荡频率下降；固定Kp2，增大Ki2时，系统振荡频率下降。但在相同的增幅下，Ki2所引起的振荡频率的变化较Kp2小。

3.2 储能系统的影响

采用风-储独立控制，当风电场从有储能系统到无储能系统时，表1 中振荡模式λ1，2，λ3，4，λ9，10，λ11，12无变化。振荡模式λ5，6，λ7，8的实部增大，阻尼比降低，系统稳定性降低，虚部变小，振荡频率下降。λ13，14振荡模式消失。

由于储能系统变流器功率外环时间常数与同步发电机等数量级，远大于后级电压环时间常数，可认为在1 个控制周期内电流环指令信号保持不变。本文通过系统频率偏差来调节储能系统的有功出力，实现频率调节，因此在分析储能系统变流器参数对振荡特性的影响时，着重研究有功功率内环PI3控制器。

对不同Kbp3，Kbi3下的特征值结果分析发现，振荡模式λ5，6的阻尼比最小，观察振荡模式λ5，6的变化情况可知，当Kbi3不变，Kbp3增大时，系统特征值实部变小，系统稳定性升高；Kbp3不变，Kbi3增大时，系统特征值实部与虚部基本不变，对系统稳定性影响很小。可见，相较于Kbi3，系统特征值对Kbp3更敏感，且Kbp3增大有利于系统稳定。

不同Kbp3，Kbi3下的主导振荡模式的振荡频率如图7 所示。

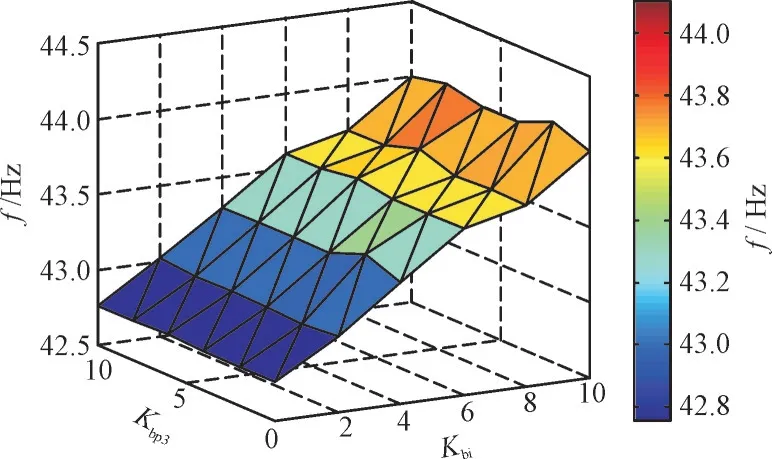
图7 不同Kbp3，Kbi3下振荡频率的变化Fig.7 Oscillation frequency variation under different Kbp3 and Kbi3

从图7 可知，Kbi3不变，Kbp3增大时，系统振荡频率升高；Kbp3不变，Kbi3增大时，系统振荡频率基本不变。

3.3 系统短路比的影响

设置电网输电线路阻抗参数使系统短路比（Short Circuit Ratio，SCR）（量值记为RSC）分别为20，10 和3.3。对不同RSC下的特征值结果分析发现，阻尼比较低的振荡模式λ5，6的变化情况如表2 所示。当电网短路比从20 降低至3.3 时，系统阻尼减小，稳定性降低。说明电网短路比较低时，即弱电网运行状态下，不利于系统稳定。

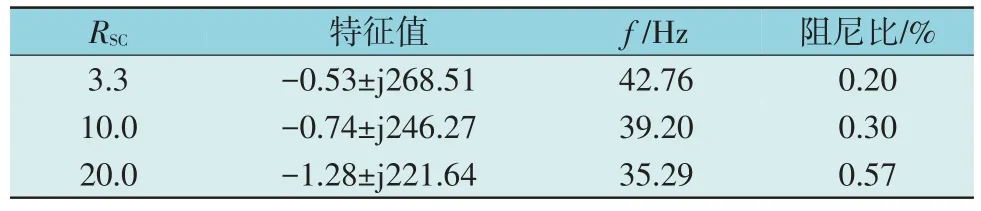
表2 不同短路比下系统特征值的变化Table 2 Eigenvalue variation under different SCRs

4 仿真验证

在Matlab/Simulink 中搭建图4 所示的含储能风电场外送仿真模型，对第3 节分析结果进行仿真验证。

4.1 储能系统变流器参数的影响

设扰动1 为风电场出口处三相短路，0.8s 后扰动消失。储能系统取不同Kbp3，Kbi3时，系统在扰动1下频率和线路功率曲线如图8 所示。

由图8 可知，随着Kbp3从1 增大至10 时，扰动消失后系统频率恢复时间缩短，最大频率偏差降低，稳态频率偏差降低，系统稳定性升高；随着Kbi3从1 增大至10 时，扰动消失后的频率响应无明显变化，说明Kbi3变化时对系统振荡特性影响较小。结合3.2 节的特征值分析结果可知，Kbp3的增大会导致系统主导特征根实部降低，系统阻尼升高，稳定性提高；而Kbi3变化时系统主导特征根不变，系统稳定性不变。

4.2 储能系统及其控制方式的影响

扰动1 下，风电场无储能、风-储独立控制和风-储协同控制下系统频率响应如图9 所示。

图9 扰动1下系统频率响应Fig.9 Frequency response under disturbance 1

由图9 可知，在扰动消失后，相较于无储能系统，风-储独立调频控制和风-储协同调频控制方法均降低了系统的最大频率偏差和稳态频率偏差，减少了系统频率稳定所需时间，改善了系统稳定性。相较于采用风-储独立调频控制，采用风-储协同调频控制方法时，扰动消失后频率波动幅度更小，稳态频率偏差也有所降低。

考虑到负荷变化会影响风-储独立控制和风-储协调2 种控制策略的效果，文中进一步设置扰动2 为1 s 时风机汇流母线处突增10 MW 负荷。风电场无储能、风-储独立控制和风-储协同控制3 种情况下系统频率响应如图10 所示。

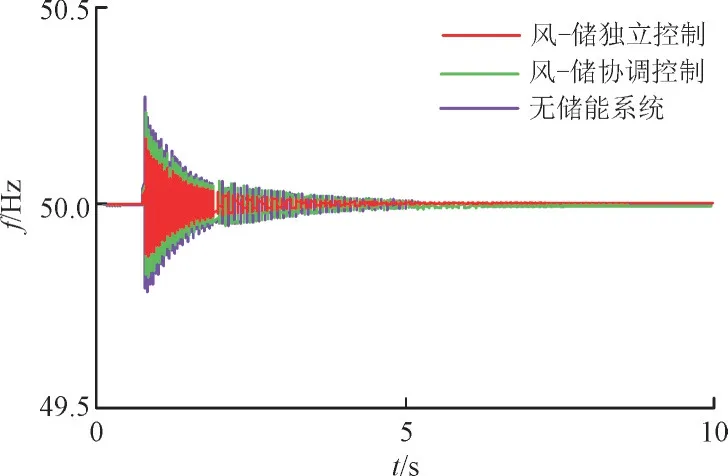
图10 负荷突增扰动下系统频率响应Fig.10 Frequency response under load surge disturbance

由图10 可知，在1 s 时系统负荷突增后，当采用风-储独立调频控制方法，负荷突增引起系统频率波动时，风电机组和储能系统同时响应于频率变化，改变自身出力参与系统频率调整。当采用风-储协同调频控制方法，由于频率变化幅度没有越过储能系统设置的死区，因此没有参与系统调频，调频容量全部由风机承担，此时系统的频率响应与无储能时一致。2 种控制方式下系统频率均可快速恢复，频率波动范围不大，系统具有较好的稳定性。可见，当采用风-储协同调频控制方法时，可充分利用风机备用容量参与系统的频率调节，避免储能系统频繁动作，使其工作寿命得以延长。相应的母线电压变化如图11 所示。

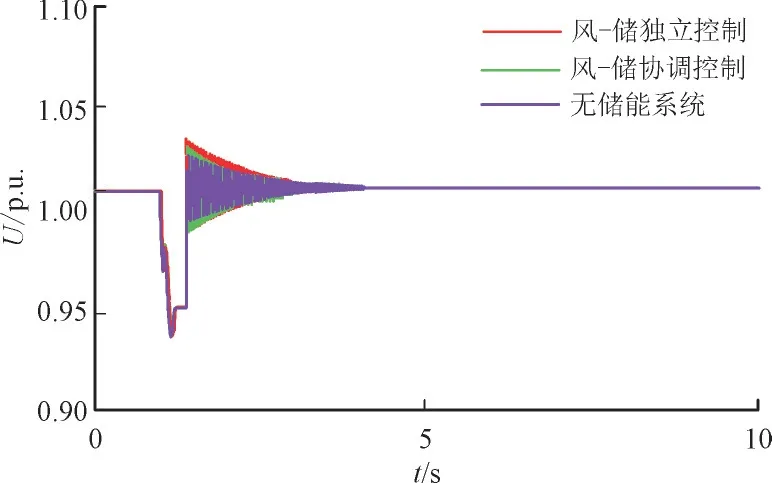
图11 负荷突增扰动下母线电压曲线Fig.11 Voltage curve under load surge disturbance

由图11 可知，负荷突增后，风-储独立调频控制和风-储协同调频控制2 种控制方法均可使母线电压恢复稳定，母线电压波动范围不大，有较好的电压稳定性。

4.3 系统短路比对振荡特性的影响

扰动1 下不同短路比的频率响应和线路功率曲线分别如图12 所示。

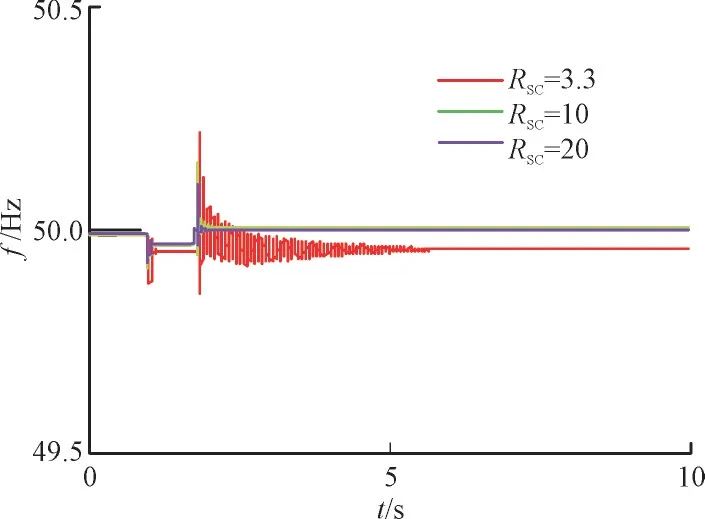
图12 不同短路比下的频率响应Fig.12 Frequency response under different SCRs

由图12 可知，随着短路比从3.3 增大至20，系统由弱电网变成强电网，系统阻尼增大，扰动消失后频率和功率恢复的更快，最大频率偏差与稳态频率偏差均降低，功率振荡幅值变小，系统稳定性更好。

5 结论

随着新能源比重升高导致传统机组容量下降，仅通过传统机组进行调频控制难以满足电力系统的调频需求。本文建立了含储能风电场参与一次调频的交流并网模型，分别研究了转子侧变流器电流内环控制参数和储能系统参数对系统振荡特性的影响。并设计了风-储独立调频和风-储协同调频2 种控制方式，对比2 种控制方式，分析其对系统稳定性的影响。主要结论有：

1）增大风电机组转子侧变流器电流内环参数Kp2和Ki2均不利于系统稳定性。

2）增大储能系统有功功率内环PI3控制器参数Kbp3，系统稳定性升高；储能系统有功功率内环PI3控制器参数Kbi3取值变化对系统稳定性影响较小。

3）增大短路比，系统阻尼增大，有利于扰动后的快速恢复。

4）本文所提的风-储协同调频控制可以在频率偏差较大时短时跟踪风机出力为系统提供更大的调频功率，最大频率偏差较独立控制减少40%，频率稳定时间减少1.5 s 左右；而在频率偏差较小时储能系统不参与调频，仅由风机充分利用其备用容量进行频率调整，由此，避免储能系统的频繁动作，延长储能系统的使用寿命，所提风-储协同调频控制策略具有优越性。