基于附加阻尼控制的风电并网系统阻尼转矩分析
伍双喜,赵仕兴,秦颖婕,闫斌杰,向丽玲,杨亚楠,李宇骏
(1.广东电网有限责任公司电力调度控制中心,广东广州 510060;2.西安交通大学电气工程学院,陕西西安 710049)
0 引言
随着越来越多的大型风电场并网,风电系统与电网的相互影响越来越复杂,导致电力系统稳定性的内在机理产生变化,这为系统稳定运行带来了挑战[1-2]。由于风力发电机组与传统同步机具有不同的原理结构与并网方式,且风能具有间歇性、随机性的特点,影响电力系统的安全稳定运行及电能质量[3-4]。风电接入会影响电力系统的阻尼特性,对于含有较高比例风电的电力系统,低频振荡问题较为突出,尤其是互联系统的区域间振荡,如果在扰动期间无法提供足够的阻尼,低频振荡将会严重影响系统的稳定[5-8]。
国内外学者已深入研究了风电并网对系统稳定运行的影响。文献[9]发现随着风电出力占比增加,电力系统振荡模式阻尼比下降,系统更易发生振荡。文献[10]通过特征值分析和动态时域仿真方法系统地分析了风电机组对电力系统稳定性的影响,文献[11]研究了不同比例风电对系统小干扰稳定性的影响,并讨论了系统的稳定裕度。由于风力发电机通过电力电子换流器接入电网,不参与系统机电振荡,当系统中风电占比提高时,阻尼振荡的能力会下降。
为了解决风电并网带来的稳定性问题,可以通过在风电机组有功或无功功率控制回路附加控制器的方法提高含高比例风电的系统的阻尼,以抑制系统低频振荡[12-14]。文献[15]提出一种通过双馈感应风机(Doubly Fed Induction Generator,DFIG)快速有功调制改善系统阻尼的方法。文献[16]基于惯性控制与下垂控制设计了DFIG 附加频率控制,并利用阻尼比和振荡频率研究了控制参数如何影响系统振荡模态。文献[17]介绍了虚拟同步机附加阻尼控制策略来抑制低频振荡的思想。文献[18]针对不同机组分别设计虚拟同步机控制和附加阻尼控制增加系统阻尼。文献[19]提出一种针对风电系统固定串补和静止同步串补的混合补偿结构的附加控制策略。文献[20]针对双馈风机与同步机间的耦合关系提出风机变惯量优化控制策略。文献[21]介绍了风机功率振荡阻尼器控制结构的详细设计方案。文献[22]基于极点配置法提出了阻尼控制器的参数设计方案。
阻尼转矩分析法可用于研究风机控制器提供的阻尼对低频振荡的影响机理[23-24],研究系统的阻尼转矩可以分析出系统稳定的关键因素。文献[25]推导出了换流器并网系统的阻尼系数。文献[26]分析了同步发电机电力系统稳定器对系统阻尼的影响,并进行参数优化以有效提高频率振荡阻尼。文献[27]全面分析了换流器控制对发电机之间的低频振荡的影响。
总体来说,现有研究工作对有新能源接入的电力系统低频振荡特性已有较深入的研究,但存在以下不足:针对新能源机组的研究方法多采用特征值分析或时域仿真方法,无法推导出附加控制与系统运行条件影响系统低频振荡模式的解析关系。文献[28-29]采用阻尼转矩分析法研究了风机引入系统的动态相互作用对振荡模式的影响,但这些研究仅分析了常规控制下风机接入对系统稳定性的影响,无法评估风机附加功率控制策略对系统阻尼的贡献。针对现有研究存在的问题,本文通过阻尼转矩分析法揭示了影响风电接入系统稳定性的关键因素,并进一步给出了主动抑制系统低频振荡的风电机组控制策略。
1 双馈感应风电机组功率控制策略
DFIG 的转子绕组通过背靠背换流器接入电网,如图1 所示。
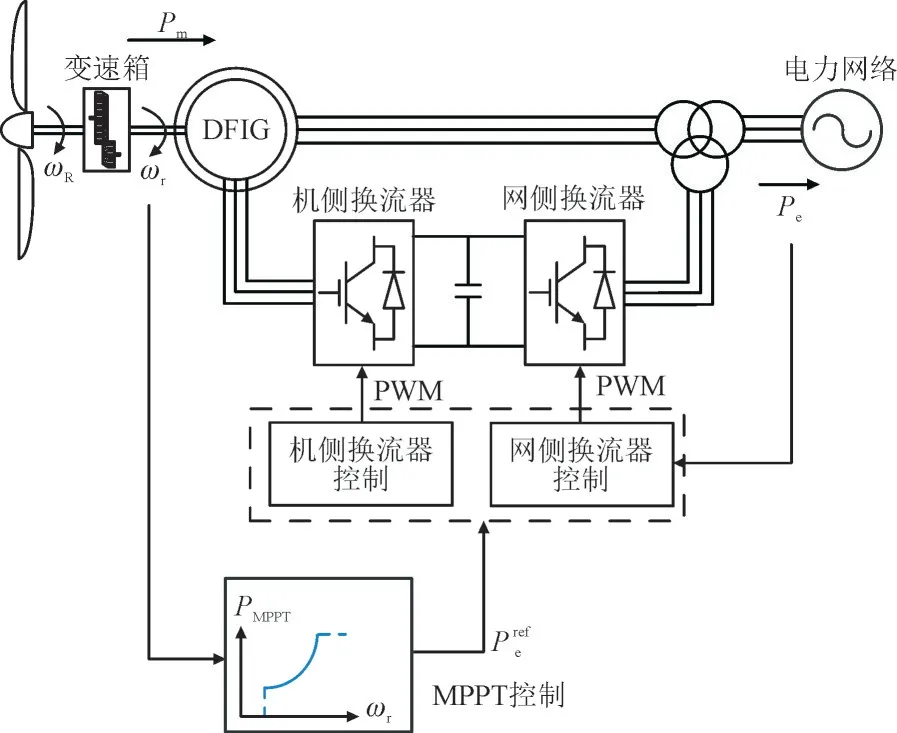
图1 连接到电力网络的双馈感应风电机组Fig.1 DFIG connected to power system.
图1 中,Pm为风轮机输出机械功率,Pe为DFIG输出有功功率,ωR为风轮机转子角速度,ωr为DFIG转子角速度,为有功功率参考值,PMPPT为最大功率点跟踪(Maximum Power Point Tracking,MPPT)算法求解出的风电机组的最大输出功率。脉冲宽度调制(Pulse Width Modulation,PWM)用于换流器控制信号处理。恒定风速下PMPPT可表示为:
式中:ρ为空气密度;R为风轮机叶片半径;Cpmax为最大风能利用系数;λ为叶尖速比;k为齿轮变速箱的变速比;K为MPPT 控制系数。
在稳态下,=PMPPT。由于背靠背换流器双回路控制具有快速响应特性,忽略换流器动态和功率损耗,认为Pe与参考值相等:
在不考虑转子阻尼的情况下,DFIG 的转子运动方程可由式(3)表示:
2 基于下垂的附加阻尼控制器
由于DFIG 换流器将风力机转子与交流电网的动态性能分离,风电机组难以在系统受到干扰时为其提供阻尼。附加下垂控制策略可向互联系统提供额外的阻尼,以抑制互联系统区间低频振荡,本文设计一种基于互联系统两区域相对角频率差值的附加阻尼控制器。有风电系统接入的区域互联系统的拓扑结构如图2 所示。
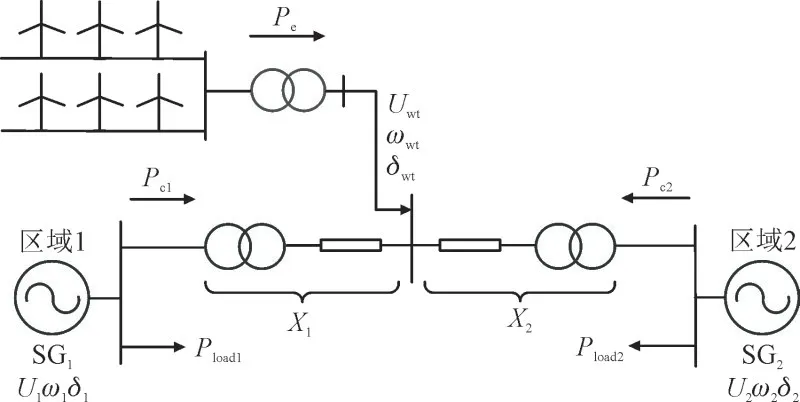
图2 有风电接入的互联系统结构图Fig.2 Structure of the inter-area system with DFIGs
图2 中,SG1和SG2为两区域的动态特性所等效的同步发电机;Ui,ωi,δi分别为区域i出口处母线电压的幅值、角频率和功角(i=1,2);Pci,Ploadi分别为区域i 输出功率和本地负载;Uwt,ωwt,δwt分别为风电机组并网点的电压幅值、角频率和功角;Xi为SGi与风电并网节点间传输线路和变压器的总电抗。
广域测量系统采集两区域角频率信号ωi并高速传递至风电机组控制器,设定两区域相对功角差δ12=δ1-δ2,相对角频率差为ω12=ω1-ω2,风电附加阻尼控制器以ω12为输入信号,控制目标为调节ω12为0。因此,式(2)中风电机组有功功率参考信号值可由式(4)表示:
式中:为下垂控制输出信号;kω为下垂控制参数。系统在稳态时,控制器输入信号ω12和控制器输出信号Δ均为0。
图3 给出了风电机组下垂控制逻辑。
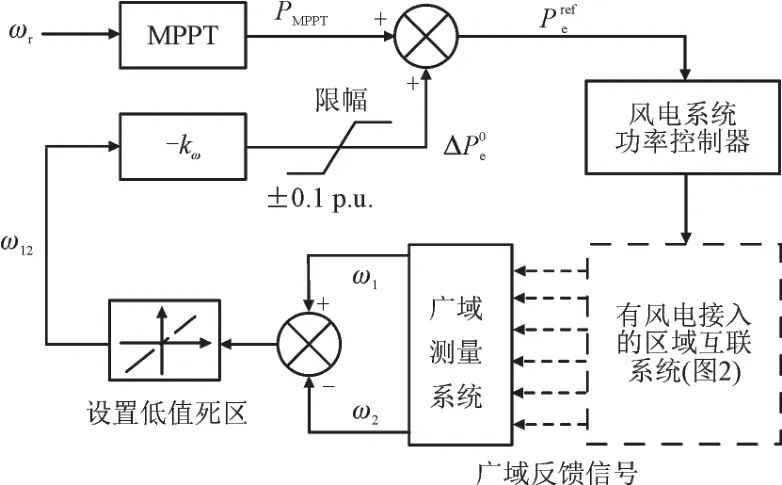
图3 风电机组下垂控制结构图Fig.3 Structure of DFIG droop control
带阻滤波器可避免控制器在系统正常运行期间对非常小的频率波动做出响应。下垂控制输出信号被限制在±0.1 p.u.范围内,以确保流过换流器开关元件的电流不超过其限额。
3 互联系统低频振荡分析
阻尼转矩分析是一种评估系统提供阻尼抑制振荡的能力的有效方法。本节基于两区域互联系统动态模型及DFIG 动态模型,推导出风电机组通过换流器控制提供阻尼转矩的表达式,并进一步分析系统阻尼转矩与具体参数之间的解析关系,评估附加阻尼控制对系统低频振荡的影响。
3.1 系统的小信号模型
对于接入两区域互联系统的风电机组,附加阻尼控制的风电系统动态模型的线性化形式为:
式中:“Δ”为变量的小扰动形式;ωr(0)为稳态下DFIG 转子角速度。
忽略同步发电机阻尼,则图2 中SGi的转子运动方程可以由式(6)表示。
式中:TJi,Pmi(i=1,2)分别为发电机SGi的惯性时间常数和机械功率;Ploadi为恒定;ωs为系统同步角频率。
基于发电机的转子运动方程可以清晰地推导出电力系统中由风电控制器引入的阻尼。风电并网点的有功功率平衡方程由等式(7)表示:
在不考虑损耗的情况下,Pci可由式(8)表示:
将式(8)代入式(7)得到功率平衡方程的线性化表达式,如式(9)所示:
式中:δi(0)和δwt(0)分别为区域i出口电压功角稳态值和风电并网点稳态值
同步机励磁系统和无功补偿装置使系统各节点的电压限制在小范围内变化,因此设Ui=Uwt=U0;同时,由于各节点功角差较小,认为cos(δi(0)-δwt(0))≈1。联立式(6)—式(9),消去Δωwt,得到由Δδ12和Δω12表示的互联系统动力学方程如式(10)所示:
式中:XΣ为两区域间线路总电抗,XΣ=X1+X2,其中X1中为区域1 和风电并网点间线路和变压器的电抗,X2中为区域2 和风电并网点间线路和变压器的电抗。
若风电输出功率保持恒定(ΔPe=0),由式(10)推导出无阻尼状态下系统的动态方程如式(11)所示,系统无阻尼自然振荡频率ωd可由式(12)求解:
式中:d2Δδ12/dt2为功角差小扰动形式的二阶导数。
3.2 系统阻尼转矩分析
式(5)表示的风电系统动态方程的Laplace 形式如式(13)所示:
式中:s为Laplace 复变量。
将式(13)代入式(10),得到式(14):
根据经典的阻尼转矩分析方法,电磁转矩可以分解为同步分量和阻尼分量,它们分别与转子功角和转子角频率同相。设系统等效惯性时间常数频域形式TJ(s2)如式(15)所示,系统阻尼转矩系数频域形式(s2)如式(16)所示:
则通过代数变换可将式(14)改写成式(17):
由于系统阻尼转矩相比于同步转矩较小,系统振荡频率可取为式(12)表示的自然振荡频率,即s=±jωd,则系统阻尼转矩系数可推导如下:
式中:A为系数,且在两区域互联系统参数及风轮机机械部分参数不变的情况下为常数。
3.3 系统稳定性影响因素
根据式(18),在两区域互联系统参数及风轮机机械部分参数不变的情况下,与风电接入节点位置(由X2TJ2-X1TJ1表征)和下垂控制参数kω相关。
3.3.1 风电并网点位置对系统阻尼的影响
风电场位置会影响系统的阻尼水平。当风电场位于互联系统两区域间的电气中心,即X1TJ1=X2TJ2时,为0。此时风机阻尼控制对区域间低频振荡没有影响,风机注入功率对振荡阻尼没有贡献。
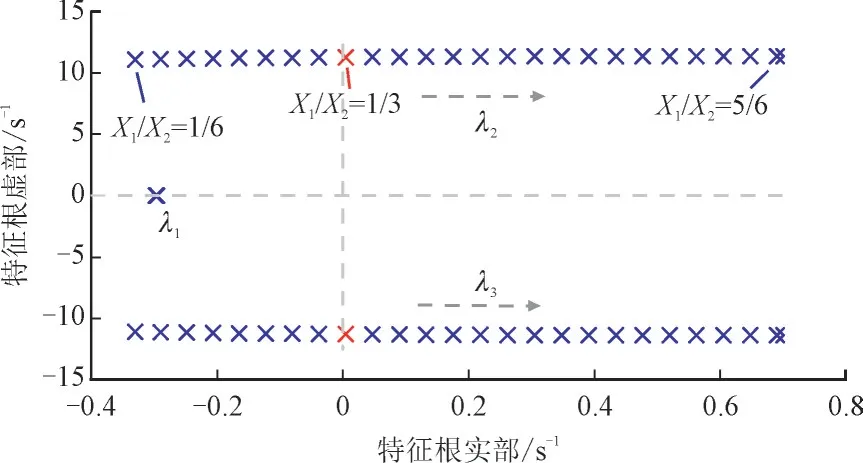
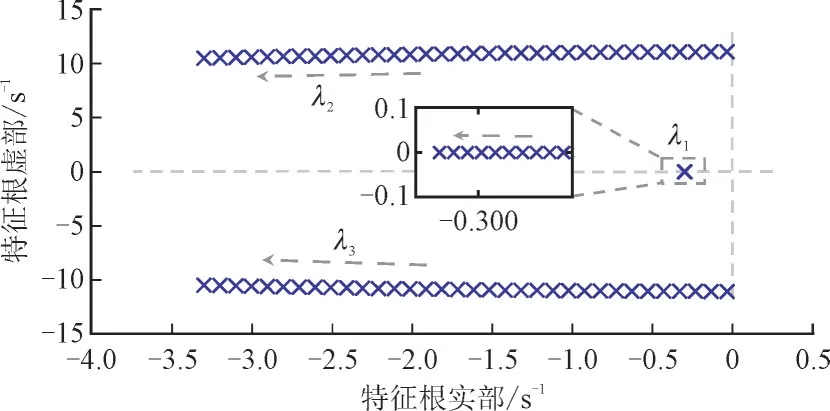
若风电场位于电气中心和SG1之间时,根据式(18),X1TJ1 相应地,若风电场位于电气中心和SG2之间,即X1TJ1>X2TJ2时,为负。风机阻尼控制有削弱系统阻尼的作用。风电场与SG2的相对位置越近,绝对值越高,对系统阻尼的削弱作用越大。当风场位于SG2节点附近时,最大负阻尼系数为: 3.3.2 控制器下垂参数kω对阻尼的影响 由式(18)可求解阻尼转矩系数K′D关于下垂控制参数kω的灵敏度,如式(21)所示: 风电场距离SG1较近时,为正,其值随kω的升高而增大。此时可通过增加kω来增强风机的阻尼性能。此外,对kω的灵敏度也受风电并网位置的影响,风电场与SG1之间的距离越近,随kω升高而更快速地增加。反之,若风电距离SG2较近,风机控制器对系统振荡起负阻尼作用,K′D的值随着kω的升高而减小。在这种情况下,较高的下垂系数会降低系统阻尼水平并恶化系统振荡。 为了说明风机控制策略对系统振荡阻尼的影响,在MATLAB 中建立了结构如图2 所示的由2 个区域电网和风力发电场组成的互联系统仿真模型。系统变量采用标幺值,且令TJ1=8 s,TJ2=4 s=8 s。 算例1 研究风电机组接入电网位置对互联系统低频振荡的影响,令kω=15。 图4 给出了系统关于风电并网点相对位置X1/XΣ的根轨迹,系统存在3 个特征根,随着X1/X从1/6 增加到5/6,即风电场位置从SG1处向靠近SG2的方向移动,主极点λ2,3向右移动并跨越虚轴。当X1/XΣ=1/3 时,根据惯性时间常数取值TJ1=8 s,TJ2=4 s可求得X2TJ2-X1TJ1=0。即风电场安装在系统区间线路电气中心位置时,λ2,3出现在虚轴上,对应系统临界稳定。 图4 系统关于X1/X的根轨迹Fig.4 Eigenvalue trajectories of X1/X 图5 和图6 分别给出了风电并网位置不同的系统受到干扰后的响应以及DFIG 状态变化。在t=2.0 s时,设SG1本地负载Pload1增加0.1 p.u.。从图5、图6可以看出,风电越远离区域1,系统低频振荡衰减越慢,恢复稳态的时间越长。其中黑色曲线表示当风电场靠近电气中心时,风电机组对系统阻尼的贡献为0,系统等幅振荡,仿真结果与式(18)的分析一致。 图5 不同风电并网位置的系统动态响应Fig.5 Simulation results of different locations of WTs 图6 不同风电并网位置的DFIG状态变化Fig.6 Variation of DFIG at different locations of WTs 图5 和图6 验证了风电并网位置显著影响系统阻尼,决定了风机对系统阻尼影响的正负。特征值分析和时域仿真结果与3.3.1 节阻尼转矩分析结论一致。 算例2,考虑与算例1 相同的扰动,研究风机控制器下垂参数kω对系统低频振荡的影响。 图7 给出了风电场设置于SG1附近时系统关于kω的根轨迹。由图7 可以看出,随着kω从1 提高至100,主导特征根λ2,3向左移动,较高的控制器参数改善了系统的稳定性。 图7 系统关于kω 的根轨迹(X1/X=1/6)Fig.7 Eigenvalue trajectories of kω(X1/X=1/6) 图8 和图9 分别给出了当风电并网点位于SG1附近时(X1/X=1/6),采用不同kω的系统遭受扰动时的动态响应和DFIG 状态变化。由图8、图9 中可以看出,随着kω增加,系统振荡衰减变快,恢复稳态的时间变短,阻尼控制器对系统区域间振荡的抑制作用更显著。 图8 采用不同控制参数的系统动态响应(X1/X=1/6)Fig.8 Simulation results with different kω(X1/X=1/6) 图9 采用不同控制参数的DFIG状态变化(X1/X=1/6)Fig.9 Variation of DFIG with different kω(X1/X=1/6) 图10 给出了风电场设置于SG2附近时系统关于kω的根轨迹,此时λ2,3位于复平面的右半部分。由图10 可以看出,随着kω升高,主导特征根λ2,3向右移动,较高的kω对系统的阻尼性能起着负面作用。 图10 系统关于kω 的根轨迹(X1/X=1/2)Fig.10 Eigenvalue trajectories of kω(X1/X=1/2) 图11 和图12 分别描述了当风电并网点位于互联系统电气中心右侧时,不同kω系统的时域仿真结果:各曲线均增幅振荡,且kω越大,振幅增长越快,系统更快地失去稳定。 图11 采用不同控制参数的系统动态响应(X1/X=1/2)Fig.11 Simulation results with different kω(X1/X=1/2) 本算例验证了kω对系统阻尼的影响。特征值分析结论和时域仿真结果与3.3.2 节阻尼转矩分析结论一致。 算例3 考虑与算例1 相同的扰动,研究风电出力占比对系统的影响,如图13 和图14 所示。从图13 和图14 的时域仿真结果可以看出,在控制参数不变的情况下,附加阻尼控制尺度相同,不同风电占比的系统对区域间低频振荡的抑制作用差距较小。 图13 不同风电出力占比的系统动态响应Fig.13 Dynamic response with different wind energy ratios 本文设计了一种基于DFIG 的附加阻尼控制器以改善两区域互联系统低频振荡的阻尼,提出了用于稳定性分析的两区域互联系统的简化数学模型,并推导出等效阻尼转矩系数的解析形式,详细评估了风机控制参数和系统运行条件对系统阻尼特性的影响。研究表明风机控制器为互联系统提供阻尼的正负主要由风场接入电网位置决定,而适当地调整控制器的下垂控制系数可以提高机组对阻尼的贡献。针对DFIG 接入两区域互联系统进行了算例研究,时域仿真结果证明了控制参数和风电接入系统运行状态对系统阻尼的影响。4 仿真分析
4.1 风电接入位置对系统振荡的影响
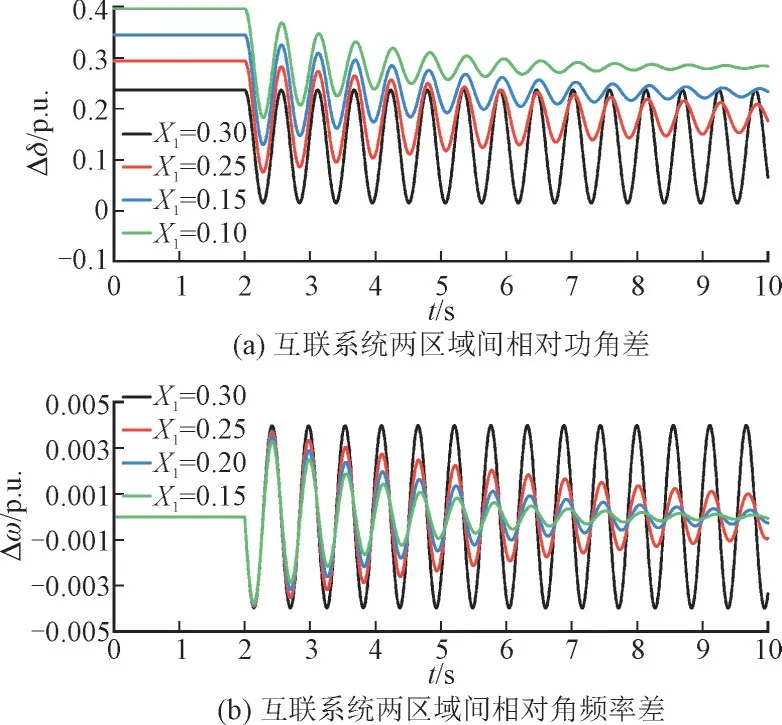
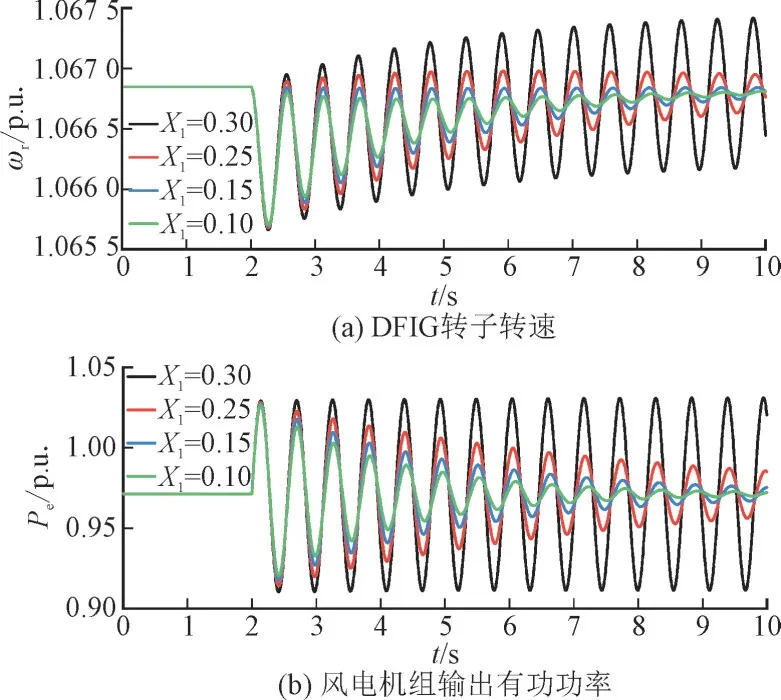
4.2 控制器参数对系统振荡的影响
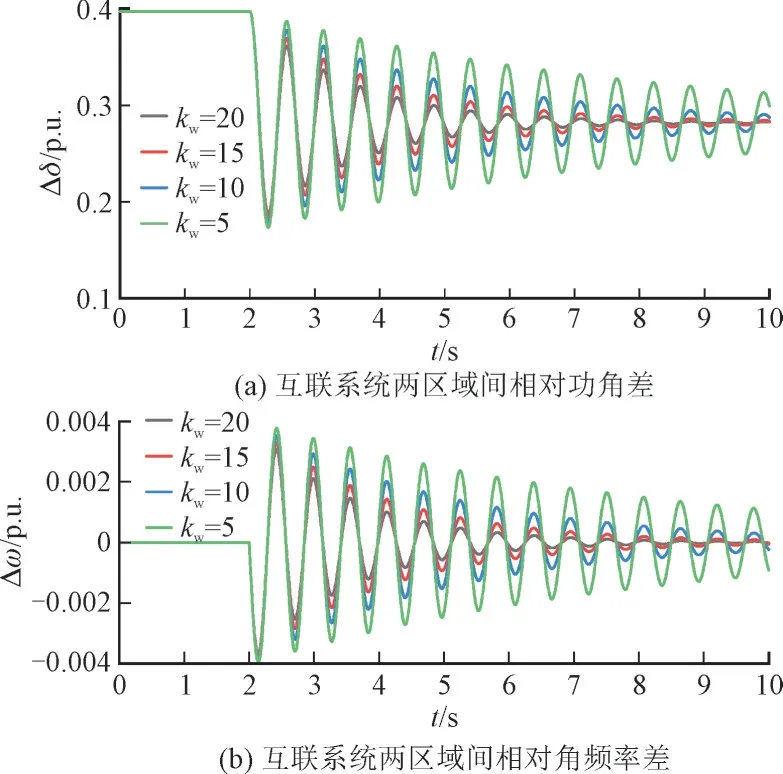
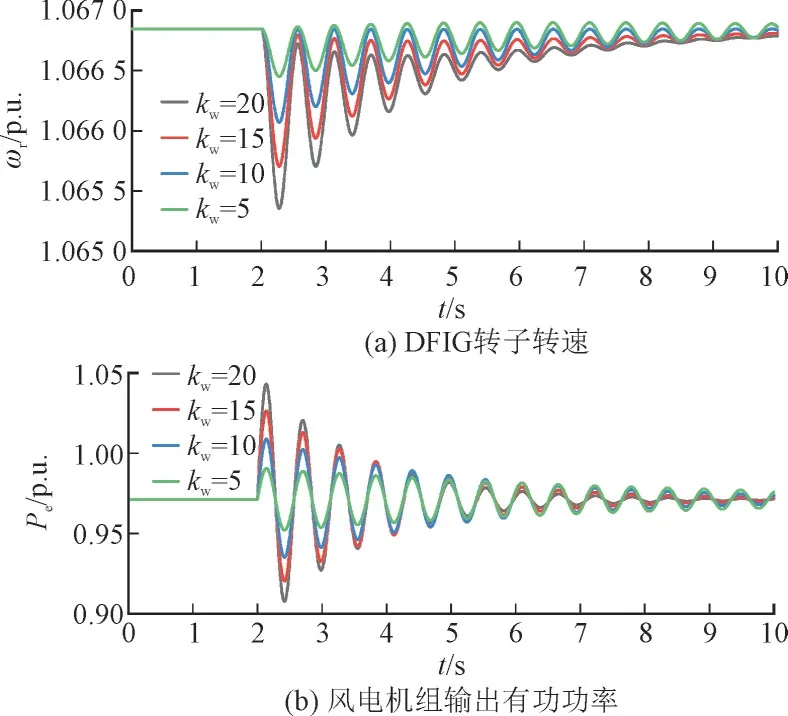
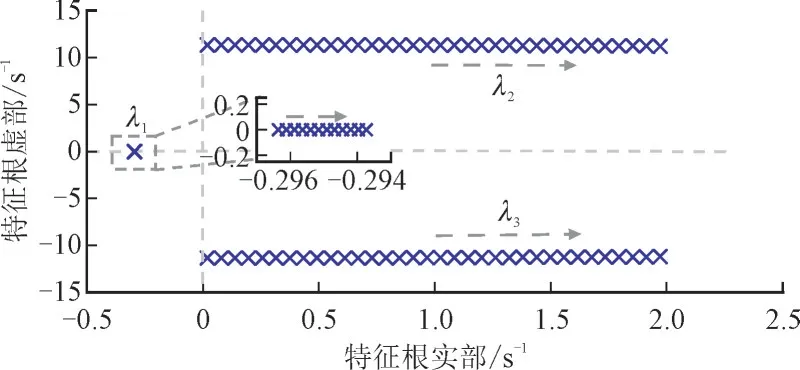
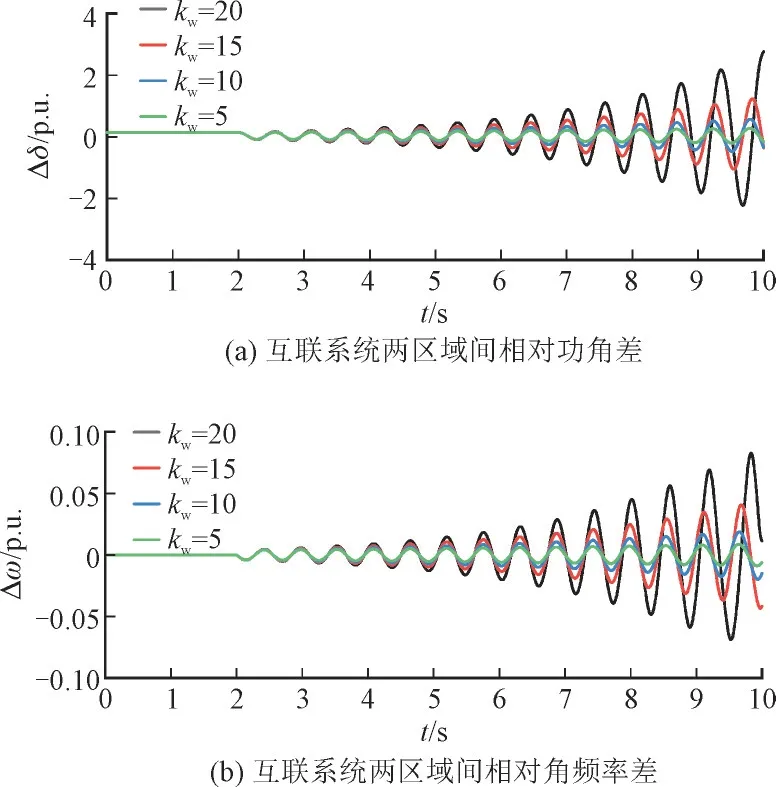
4.3 风电出力占比对系统振荡的影响
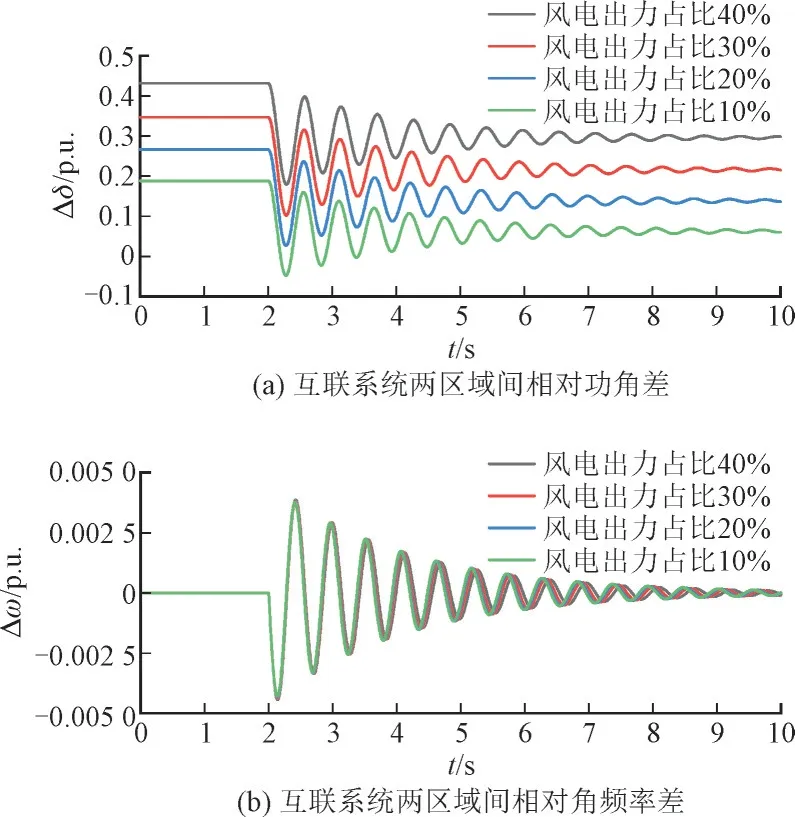
5 结语

