基于汇集点处PMU测量的聚合电源等效惯性常数估测方法研究

莫 若，邓小宇，蔺 红，刘牧阳

（新疆大学电气工程学院，新疆乌鲁木齐 830063）

0 引言

为了“双碳”目标的实现，我国正在建设以风电、光伏等新能源为主体的新型电力系统[1]。传统的同步发电机（Synchronous Generator，SG）逐渐被风、光等基于电力电子逆变器接口的新能源电源所取代，系统安全稳定性面临严峻挑战[2]。为应对低惯量带来的挑战，电力电子接口电源为电网提供虚拟惯性的技术得到大力发展，其中部分技术，诸如虚拟惯性控制技术[3-5]和同步虚拟机技术[6-8]，已经被证明可以有效提高电力系统的稳定性和安全性。随着此类技术的发展与落地，基于电力电子逆变器控制的虚拟惯量也将成为系统重要的惯量来源[9]。

当前电力系统仅通过数据监控及采集（Supervisory Control and Data Acquisition，SCADA）系统读取同步机组启停状态进而估测系统的转动惯量水平[10]，无法对可调可变的虚拟惯量进行监测，需发展新一代综合惯量估测技术。相量测量单元（Phase Measurement Unit，PMU）与广域测量系统（Wide-Area Measurement System，WAMS）的广泛运用[11-12]为发展高准确率、高实时性的电力系统综合惯量估测技术奠定了良好基础。

现有的综合惯量等效惯性常数估测技术可以分为两类。一类根据系统对大型频率事件（例如负荷突变和系统N-1 事件）的响应来估测各电源的等效惯性常数[13]。为了避免该问题，另一类基于电网侧PMU 的常态化测量数据的等效惯性常数估测技术应运而生。此类技术可以实现对系统惯性水平的连续监控，但其面临的主要问题是对测量噪声的鲁棒性较差，需要清洗PMU 测量数据，以减轻测量噪声的影响[14-15]。基于常态化PMU 测量数据的电源等效惯性常数估测技术，文献[16]通过对频率信号进行微分计算从而获得的频率变化率（Rate of Change of Frequency，RoCoF）进而估测机组等效惯性常数，该方法数值稳定性较差、准确性低，且计算量较大。文献[17]利用PMU 时序测量数据估测功率变化率和RoCoF，采用最小二乘算法（Least Square Method，LSM）进行惯量估测，该算法的复杂度低，结构较为简单、数值稳定性高且易于实现，但存在过拟合问题，其准确性有待提升。

本文采用基于PMU 测量的惯量估测技术结合Tikhonov 正则化算法，提出了一种综合惯量等效惯性常数估测方法，该方法可及时准确地估测安装有PMU 的主要电源汇集点（Point of Interconnect，POI）处接入的聚合电源的等效惯性常数，有效避免LSM 的过拟合现象，对等效惯性常数估测结果具有较高的准确性与测量噪声鲁棒性。基于该方法获取的各汇集点惯量信息可实现对系统综合惯量水平的在线估测。

1 聚合电源等效惯性常数

1.1 聚合电源等效惯性常数的定义

聚合电源是指在主网汇集点处可视为一个等效电压源的同步发电机、新能源及储能的一种或多种电源装备的多机聚合，可为系统提供包括转动惯量或（及）虚拟惯量。聚合电源具体形式如图1 所示，聚合电源可由虚拟同步机（Virtual Synchronous Generator，VSG）组和同步机组聚合而成，VSG 可由新能源及储能的一种或多种电源装备所构成，同步机组可由一个或多个同步机所构成。当系统频率发生波动时，具有惯量支撑能力的聚合电源可为系统提供惯量来削弱频率变化率，进而阻碍系统频率变化。聚合电源具体形式如图1 所示。

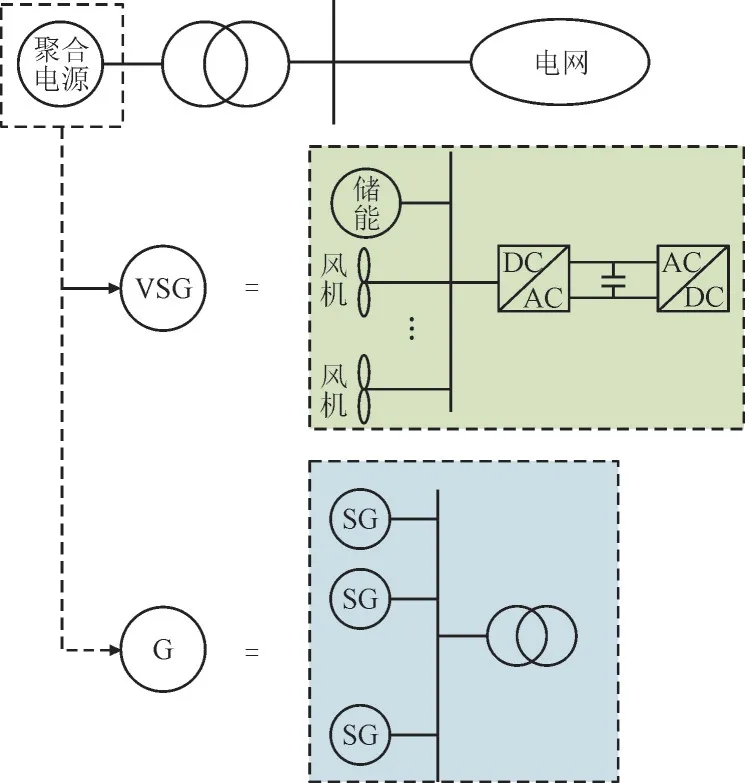
图1 聚合电源Fig.1 Aggregated power source

等效惯性常数物理定义由同步发电机的摇摆方程[18]推导而来，其标幺值形式为：

式中：HSG为同步发电机的等效惯性常数；为同步发电机的角频率；Pm为同步发电机的机械功率；Pe,SG为注入电网的电磁功率。

参照式（1），可推知聚合电源标幺值形式下的机电动态方程为：

式中：H为聚合电源等效惯性常数；为聚合电源等效角频率；ΔP为聚合电源功率变化量，可分解为：

式中：PUC为调度控制中心提供的功率参考点；PPFC和PSFC分别是由一次频率控制（Primary Frequency Control，PFC）和二次频率控制（Secondary Frequency Control，SFC）调节的有功功率；Pe为等效聚合电源的电气功率。

当角频率发生变化时，具有惯量支撑能力的聚合电源将惯量转化为电气功率从而抑制频率变化。

考虑到电力系统的惯量主要由电源侧提供，负荷侧惯量相对较小，因此，已知系统主要聚合电源的惯量信息，即可对系统综合惯量水平进行估测。由N个聚合电源进行供电的电力系统，其等效惯性常数估算方法为：

式中：Hsys为系统的等效惯性常数；Hi为第i个聚合电源的等效惯性常数；Si为第i个聚合电源的额定容量；Ssys为系统总额定发电容量。

1.2 等效惯性常数估测原理

结合后将式（2）和式（3）求关于时间的微分，可推导出：

式中：为聚合电源等效角频率二阶导数；为调度控制中心提供功率参考点的一阶导数；分别为由PFC 和SFC 调节有功功率的一阶导数；为等效聚合电源电气功率的一阶导数。

与可通过PMU 测量获得的有功功率与角频率的时序数列进行计算处理获得。由此可知，聚合电源的等效惯性常数估算可根据其有功功率变化和频率变化进行估测。

1.3 常态化等效惯性常数估测及存在的问题

实际电力系统在正常运行状态下，仍受到由新能源与负荷随机波动造成的小干扰影响，电源有功出力与频率围绕额定值波动，处于动态平衡状态。由式（6）可知，根据聚合电源汇集点处安装的PMU捕获系统正常运行状态下的频率和有功出力的动态可以分析系统的等效惯性常数。系统小干扰造成频率波动的特点是频次较高、幅值波动较小，容易与测量噪声交叠。因此，基于式（6）的等效惯性常数辨识必须考虑由测量噪声所带来的误差，故在实际系统中存在式（7）的关系：

式中：H∗为等效惯性常数估测值；为有功功率估测值；为角频率估测值；ζP，ζω分别为有功功率和角频率因测量噪声而产生的测量误差。

通过分析式（7）可知，在等效惯性常数估测过程中，当分母+ζω值趋于0 时分子中测量误差ζP的影响将通过无穷小的分母被显著放大，导致H∗估测结果存在严重误差。因此，保证等效惯性常数估测的有效性必须保证算法对测量噪声具有较强鲁棒性。

2 基于Tikhonov 正则化算法的等效惯性常数估测方法

2.1 聚合电源等效惯性常数估测过程

根据式（6）提出基于聚合电源汇集点处PMU 测量的聚合电源等效惯性常数估测方法，其重点在于采用Tikhonov 正则化算法对聚合电源等效惯性常数进行估测。本文所提方法的估测过程如图2 所示，图中PMU 可采集母线上的电压信号，电流信号，频率信号，对频率信号可进行微分计算获得RoCoF。

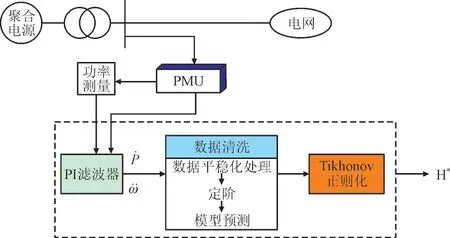
图2 电源POI处等效惯性常数估测过程Fig.2 Identification process of equivalent inertia constant at POI of power supply

由图2 可以看出，本文所提方法包括以下过程：从聚合电源汇集点处的PMU 收集RoCoF 和有功功率测量数据，通过PI 滤波器[19]获取，；然后使用自回归滑动平均（Auto Regressive Moving Average，ARMA）模型清洗数据；清洗后的数据输入Tikhonov 正则化算法以此完成等效惯性常数估测。

2.2 数据清洗

由式（7）可知PMU 测量噪声对等效惯性常数估算的准确性存在严重影响，故本文使用ARMA 模型进行数据清洗，削弱测量噪声影响。

对于PMU 测量噪声的统计学特点[20]，文献[21]通过从高、中、低压电网中PMU 测量的电压幅值、电流幅值和频率相对应的现场数据的噪声分布，分析出所有数据集的噪声分布可近似模拟成均值为0的高斯分布。其中，测量噪声的信噪比（Signal-to-Noise Ratio，SNR）值以dB 为单位，其计算公式为：

式中：σ为标准偏差。

一般PMU 测量噪声的SNR 范围为43～92 dB。

2.3 基于Tikhonov正则化算法的等效惯性常数辨识

经ARMA 清洗后tj时刻的，作为输入数据，可将式（7）改写为式（9）：

式中：为tj时刻的等效惯性常数估测值；为tj时刻的有功功率估测值；(tj)为tj时刻的角频率估测值。

考虑到具有惯量水平效果的聚合电源等效惯性常数必为正数，同时为减少符号位的储存，式（9）对输入数据采用绝对值形式进行等效惯性常数估测，并可改写为：

式中：ε为估测与实际值的误差。

越接近实际的等效惯性常数，则误差值ε越接近于0。

等效惯性常数估测的测量时间窗长度值为tj-t1。t1至tj时刻的，可分别构成时序数列A和b：

结合式（10）和式（11）构建了基于LSM 的等效惯性常数估测，即求解：

由于LSM 存在对数据过度拟合的问题，Tikhonov 正则化算法则以式（12）为基础加入正则项，可以有效避免过拟合问题。为方便式（13）表述，令x=H∗。Tikhonov 正则化算法的表达式LT(x)为：

式中：λ为正则项系数。

正则化系数λ可以控制模型正则化的程度。如果出现过拟合现象，增加λ值，正则化惩罚将会相应地提高，整体损失函数将不会收敛，从而略过可导致过拟合的数据。

若要满足等效惯性常数估测值的误差最小，则LT(x)对x求偏导的结果需为0。对式（13）求偏导，即：

式中：E 为单位矩阵。

3 算例分析

本节采用一种改进的高比例新能源WSCC 9 总线系统，验证本文所提的等效惯性常数估测方法的有效性。改进的WSCC 9 总线系统如图3 所示。

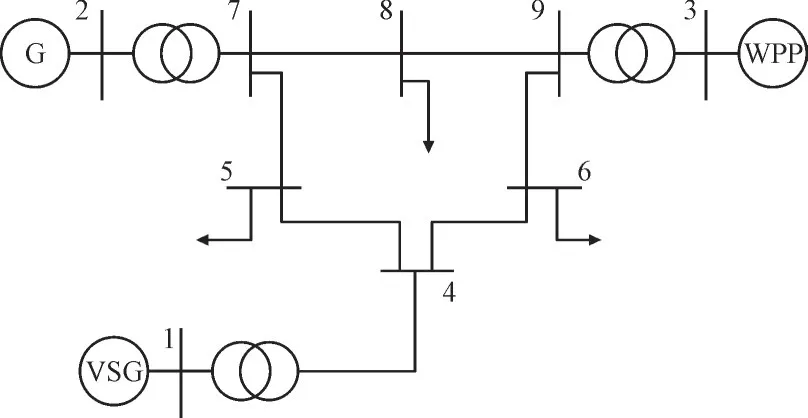
图3 改进的WSCC 9总线系统Fig.3 Modified WSCC 9-bus system

改进的WSCC 9 总线系统包含9 条母线，母线1 连接VSG；母线2 连接同步发电机组；母线3 连接风力发电站（Wind Power Plant，WPP）；母线4、母线5、母线6、母线7、母线8、母线9 均传输电能。VSG的额定发电容量为0.85 MW，其具体动态模型由文献[22]提供；同步发电机组额定发电容量为0.8 MW，其具体动态模型由文献[23]提供；WPP 额定发电容量为0.8 MW，其具体动态模型由文献[23]提供。其中，VSG 和SG 的等效惯性常数分别为HVSG=10 s，HSG=23.64 s，由于风电场惯量相较于同步机、虚拟同步机而言极小，故假定其不参与系统惯量响应。风速的动态变化即系统在正常运行状态下遭受的连续不断的小扰动，风速模型是根据韦伯分布构建的随机时序模型。假定聚合电源汇集点1 号、3 号母线上均安装有采样频率为10 000 Hz 的PMU。在基于Python 的DOME 软件[24]中编写Tikhonov 算法，完成等效惯性常数的估测并进行仿真验证。等效惯性常数估测结果的相对误差δ，可表示为：

不考虑测量噪声的情况下，VSG 电源汇集点即母线1 处测得的输出有功功率和频率变化率的数据如图4 所示。

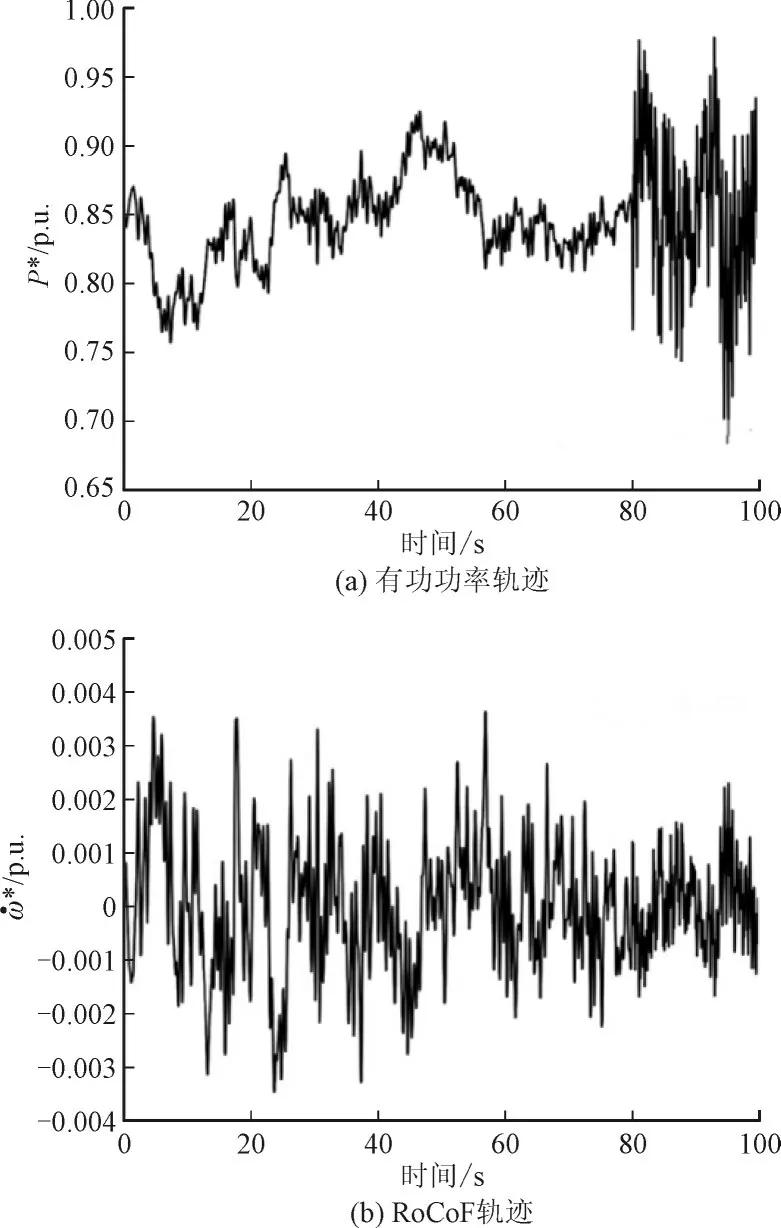
图4 测量信号Fig.4 Measured signals

因PMU 测量噪声是由传感器和信号处理中的误差所产生的，故系统所有类型数据的SNR 误差均为相似[21]。本节考虑各母线处PMU 存在均值为0的高斯分布测量噪声信号，此测量噪声信号满足2.2 节中测量噪声特性。文献[25]指出PMU 测量数据时SNR 值越大，则数据携带的噪声就越少，对输出数据的影响越小。由此可知，在满足PMU 的SNR 标准范围内SNR 值越小，测量噪声对等效惯性常数估测的影响越大。为更好展示本文所提方法对等效惯性常数估测的准确性和对测量噪声的强鲁棒性，在测量噪声极端恶劣情况（即SNR 值为43 dB）对聚合电源的等效惯性常数进行估测。本节测量噪声信号如图5 所示。

图5 噪声信号图Fig.5 Noise signal diagram

3.1 转动惯量的等效惯性常数估测效果

本节分析了λ值选取对本文所提等效惯性常数估测方法准确性的影响，并论证了Tikhonov 正则化算法对转动惯量的等效惯性常数估测的准确性。

考虑到同步发电机组的等效惯性常数在正常运行状态下为固定值，且通常其固定值可知，故本节采用改进的WSCC 9 总线系统中2 号母线上的同步发电机组的等效惯性常数估算结果为参考，选择适宜的λ值。在长度为7 s 的测量时间窗内，不同λ取值对SG 等效惯性常数估算结果的影响误差如图6 所示。

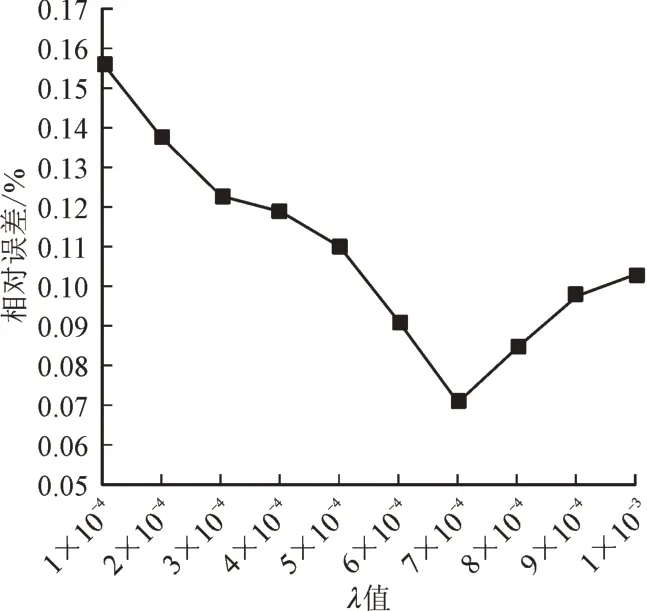
图6 不同λ 取值的SG等效惯性常数估测Fig.6 Equivalent inertia constant identification of SG with different λ values

由图6 可知，λ值与测量误差呈现二次函数关系，即针对特定的测量时间窗存在使测量误差最小化的最佳值。经测试，最佳λ值为7.0×10-4，其对应的等效惯性常数估算结果误差为0.07%，文章剩余实验部分所采用的λ值均取7.0×10-4。

2 号母线上的同步发电机组采用Tikhonov 正则化算法进行等效惯性常数估测，表1 列出了不同测量时间窗的估测结果。

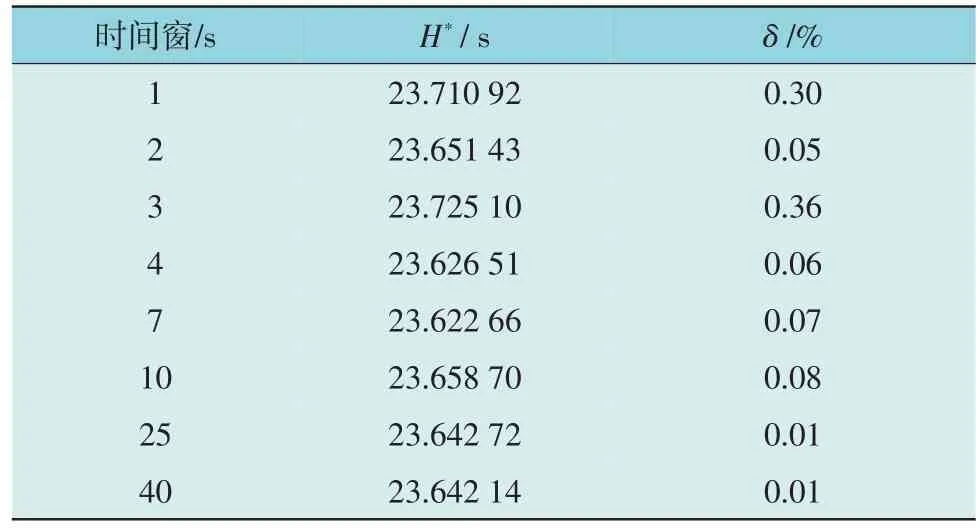
表1 常态化测量的SG等效惯性常数估测结果Table 1 Equivalent inertia constant identification results of SG in normalized measurements

因前期数据量不足，估测结果受单一时刻数据影响大，1～3 s 内的相对误差具有一定偶然性。当时间窗选取长度为4 s 及以上后，等效惯性常数估测误差稳定收敛至0.1%以下。由表1 可知，本文所提方法对SG 等效惯性常数估测的相对误差在1～40 s测量时间窗中分布在0.01%～0.36%范围内，其准确度极高。

3.2 虚拟惯量的等效惯性常数估测效果

本节为了验证所提方法对虚拟惯量等效惯性常数估测的准确性和测量噪声的鲁棒性，分别在理想化状态（无测量噪声）和正常运行状态（有测量噪声）下对VSG 等效惯性常数估算，估测结果如表2所示。为了更清晰地展示出所提方法对测量噪声的鲁棒性，对估测结果进行曲线化，如图7 所示。

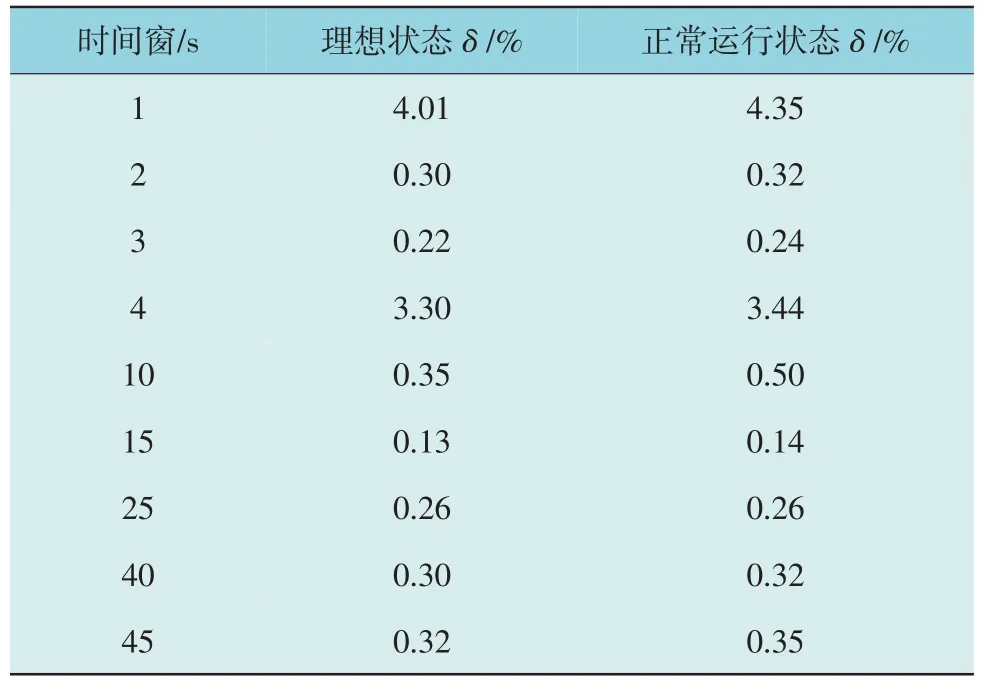
表2 2种状态下VSG等效惯性常数估测结果Table 2 Equivalent inertia constant identification results of VSG under two different states

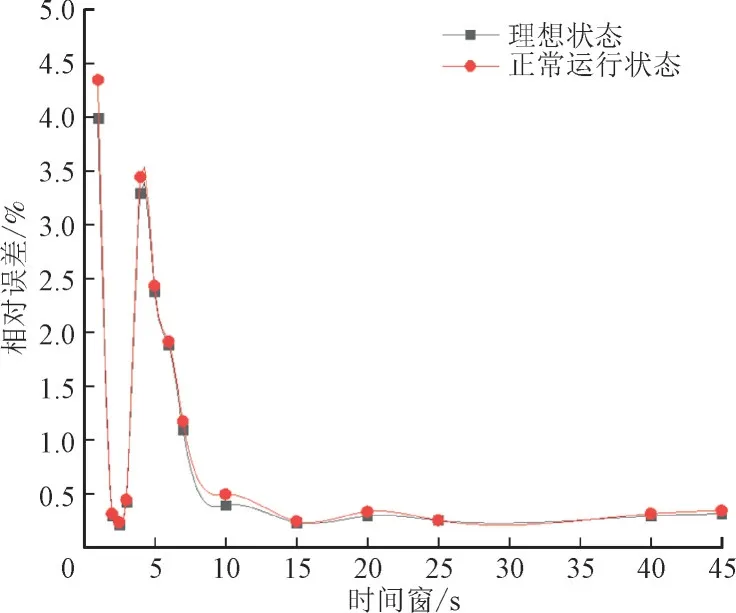
图7 理想状态和正常运行状态下VSG等效惯性常数估测Fig.7 Estimation of VSG equivalent inertia constants in ideal and normal operating states.

由图7 可以看出，VSG 在理想状态和正常运行状态下的等效惯性常数估测结果相差范围在0.00%～0.34%，所提方法对虚拟惯量等效惯性常数估测时的准确性较高，且对测量噪声具有较好的鲁棒性。在1～45 s 的测量时间窗，存在测量噪声情况下，VSG 等效惯性常数估测的相对误差范围为0.14%～4.35%。对10～45 s 的测量时间窗，其相对误差可降至0.5%以内，展现出对虚拟惯量等效惯性常数估测的准确性。因10 s 时间窗下两种状态的结果相差较大，拟合结果图如图8 所示。

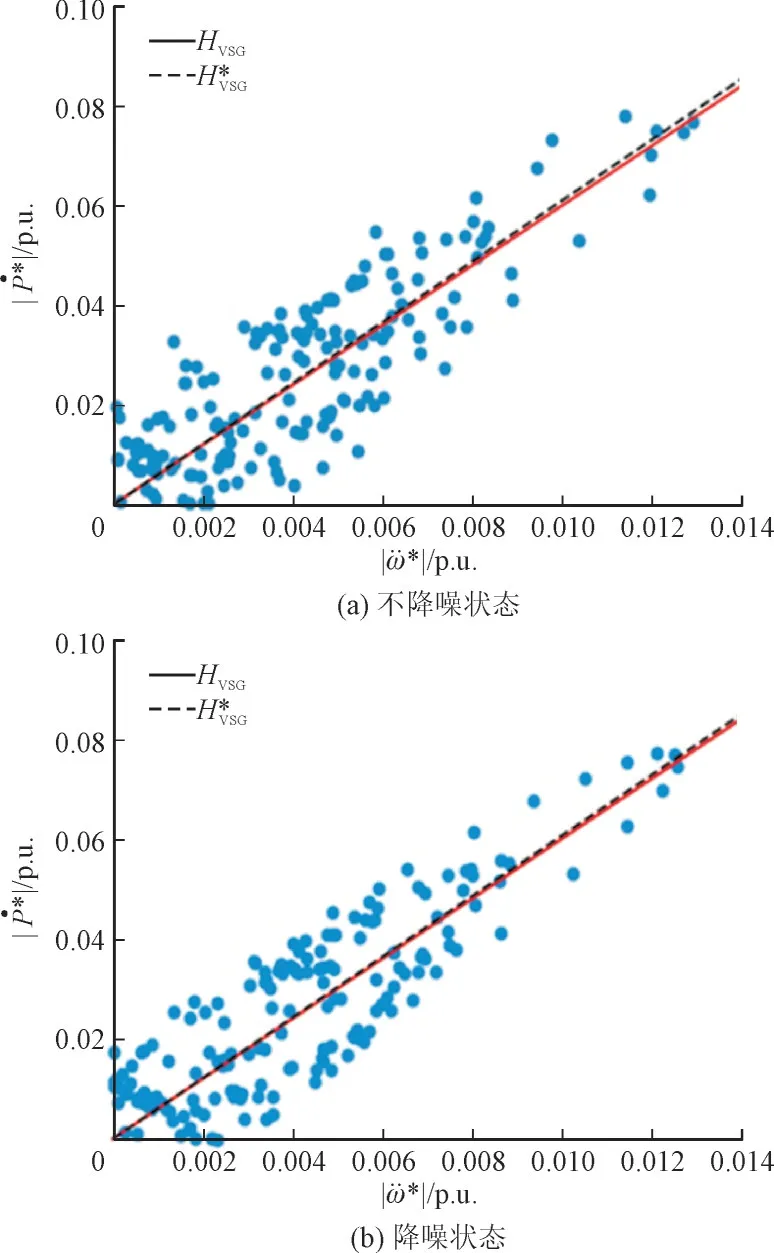
图8 VSG在10 s时间窗的等效惯性常数估测Fig.8 Equivalent inertia constant identification of VSG in 10 s time window

由图8 可知，数据清洗后的数据点明显减少，并且在拟合线附近的分布更加均匀，相对测量误差减少0.30%，故ARMA 数据清洗可有效剔除等效惯性常数估测的异常值，提升等效惯性常数估测准确性。

3.3 系统综合等效惯性常数估测效果

本节展示了文章所提方法对系统综合惯量水平监测的适用性。在实际电力系统中，关键聚合电源的汇集点处必定安装有PMU，故可对系统中的聚合电源进行有效的等效惯性常数估测，若将相关信息进行汇集，即可通过式（4）对系统等效惯性常数Hsys进行计算，从而获知系统惯量水平。改进的WSCC 9 总线系统的综合等效惯性常数Hsys=11.2 s。汇集和后计算得出的系统等效惯性常数估测结果如表3 所示。

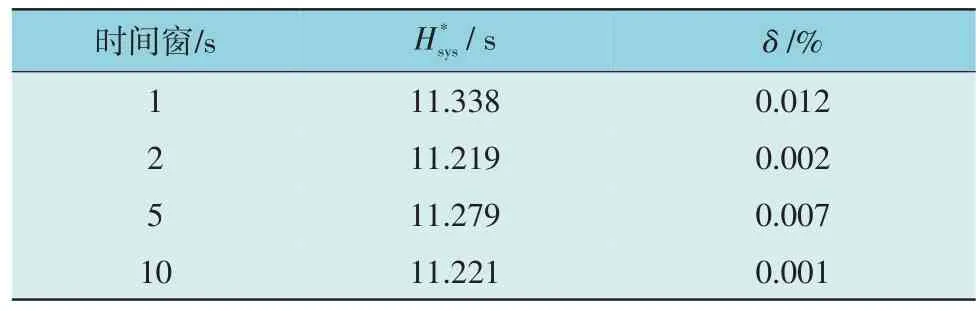
表3 系统等效惯性常数估测结果Table 3 Equivalent inertial constant recognition result of system

由表3 可知，汇集系统中转动惯量与虚拟惯量的等效惯性常数估测结果计算出的系统等效惯性常数与实际值的相对误差不超过0.015%，因此本文所提方法可用于准确评估系统综合惯量水平。

4 结论

本文针对汇集点处PMU 测量的聚合电源，提出了一种基于Tikhonov 正则化算法的等效惯性常数估测方法，并通过算例分析得出如下结论：

1）所提方法对转动惯量、虚拟惯量的等效惯性常数估测结果的相对误差分别不超过0.08%（测量时间窗范围为4～40 s）和0.50%（测量时间窗范围为10～45 s），具有极高准确性。

2）所提方法对PMU 测量噪声具有较强的鲁棒性。

3）通过准确估测新型电力系统中各主要聚合电源等效惯性常数，可对全系统惯量水平进行准确及时的估测。