可编程交流电源的分数阶多重复控制技术研究

杨鸿宇，周克亮，唐 超，柯浩雄

（武汉理工大学自动化学院，湖北武汉 430070）

0 引言

可编程交流电源需生成各种频率和波形的周期性电压波形，用于多种工业产品的设计测试等[1-5]。众所周知，重复控制（Repetitive Control，RC）可对频率已知的周期信号实施零误差补偿，为可编程交流电源提供了一种精准的输出电压控制方法[6-13]。然而，当应用于电力电子功率变换时，重复控制器目前仅用于处理单个基波频率的周期性信号。对于需要生成含有多个基波频率的多周期电压波形的情形，例如含有谐波与间谐波的电力线路扰动，可采用将多个重复控制器并联在一起所构成多周期重复方案[8-14]。

然而，由于重复控制器中需包含整数阶Ni的延迟单元z-Ni，才能对相应周期为Ni的周期性信号实现零误差补偿[13]，其中Ni=fs/fi，fi和fs分别为相应周期信号的基频和系统采样频率。受限于内置z-Ni，重复控制器的动态响应通常较慢。另外，无论采样系统频率fs是固定的还是可变的，由于多周期信号中的任意2 个基频之间的比值是非整数，最多只会有1 个基波频率信号的周期Ni为整数，其余的基波频率信号的周期Nj皆为分数。由于无法直接实现分数阶的延迟单元，常规的重复控制器只能准确补偿周期Ni为整数的周期性信号，于是多重复控制器将无法精确补偿多周期信号。

本文为可编程交流电源提出一种由多重复控制器与状态反馈控制器优势互补组合而成的多重复控制（Multi-Repetitive Control，MRC）方案及其分析与设计方法，其中多重复控制器为多周期信号提供精确补偿，而反馈控制器则提供快速动态响应和良好的鲁棒性。为克服常规多重复控制器无法精准调节多周期信号的不足，提出了将多重复控制器分数阶化的解决方案[14-22]。作为应用实例，搭建了一个3 kVA 单相脉冲宽度调制（Pulse Width Modulation，PWM）逆变器，实验验证了分数阶多重复控制方案的有效性。

1 分数阶多重复控制策略

1.1 MRC方案

图1 给出了一个插入式数字MRC 系统，其中GM(z)表示多重复控制器，Gc(z)表示常规反馈控制器，Gp(z)表示被控对象，r(z)为参考输入信号，y(z)为输出信号，e(z)为跟踪误差，d(z)为干扰信号。

图1 插入式MRC系统Fig.1 Plug-in MRC system

从参考输入r(z)和扰动d(z)到输出y(z)的传递函数为：

式中：H(z)为不含GM(z)的闭环反馈控制系统从r(z)到y(z)的传递函数。

图1 所示的插入式多重复控制方案由多重复控制器与状态反馈控制器优势互补组合而成，其中多重复控制器为多周期信号提供精确补偿，而反馈控制器则提供快速动态响应和良好的鲁棒性。

由式（1）和式（2）可以得出，若满足以下2 个条件，则多重复控制系统是渐近稳定的：（1）1+Gc(z)GP(z)=0 的根在单位圆内，即H(z)是渐近稳定的；（2）1+GM(z)H(z)=0 的根在单位圆内。

多周期重复GM(z)由多个重复控制器并联而成，可以写为：

式中：m为并联的重复控制器的数目；Gi(z)为第i个基频信号的重复控制器；ki为控制增益；Fi(z)为相位超前补偿器；Q(z)为低通滤波器。

在Q(z)带宽范围内，即 |Q(z)|≈1，GM(z)可以对多周期信号实现零误差跟踪。由式（3）可知，多周期重复控制器的设计需要确定增益ki和补偿器Fi(z)，而所有周期Ni（无量纲）都是已知的。

1.2 多重复控制器的设计

式（2）中反馈控制系统的传递函数可改写为：

式中：c为已知的延迟步长；A(z)为闭环系统的特征方程，A(z)=0 的所有根都在单位圆内；B-(z)为包括B(z)在单位圆上、圆外的根；B+(z)为包括B(z)在单位圆内的根。

为了简化重复控制器设计过程，补偿器Fi(z)可选作：

式中：b为常数，b≥max|B-(z)|2，于是：

式（6）中补偿器Fi(z)实现了对H（z）零相位补偿。

由式（1）—式（7）可知，当满足以下2 个条件时，图1 所示的数字MRC 系统是渐近稳定的[22-25]，一是H(z)渐近稳定；二是控制增益ki≥0，且增益总和K满足

给出设计如图1 所示的MRC 系统的增益稳定性判据，与现有的各种重复控制器[26-27]的增益稳定性判据完全兼容。

需要指出的是，在实际中可以用线性相位超前补偿器Fi=zp代替式（6）中的零相位补偿器，zp为实际补偿拍数，来补偿各种系统延迟（包括建模的延迟元件z-c和其他未建模的延迟）[28-30]。由于未建模的延迟（如采样延迟、计算延迟等）事先是未知的，步长p需要通过实际实验来确定。

众所周知，重复控制器Gi(z)采用较大的增益ki将产生更快的动态响应。然而，若ki选取不当，多重复控制器GM(z)将不能获得快速的整体动态响应。为保证GM(z)获取快速的整体动态响应，可遵循增益整定规则选取增益ki。

多周期信号γ(t)可写为：

式中：ωi为第i个基频信号的角频率；γi为在第i基频角频率ω=ωi处的幅值。

依据式（8）将ω=ωi处的信号占总信号的比例定义为：

式中：pi为n次谐波占总谐波的比例。

在给定多重复控制器增益总和K的情况下，各控制增益取

则GM(z)在各基波频率处的误差收敛速度将保持一致。于是GM(z)的整体动态响应速度将与K成正比例，即K越大，整体动态响应速度越快。需要指出的是，由于实际中无法准确实现式（6）中的零相位补偿，K或ki的稳定上限往往明显小于2[29-30]；此外，过大的K或ki可能会导致阻尼不足，易导致过冲振荡响应[30]。

1.3 分数阶多重复控制器

无论采样频率fs是固定的还是可变的，由于多周期信号中的任意2 个基频信号的周期比值（j为阶数，j≠i）均为非整数，最多只会有1 个基波频率信号的周期可为整数，其余的皆为分数。当Ni为非整数时，延迟环节，其中[Ni]是Ni的整数部分，Di=Ni-[Ni](0 ≤Di<1)是Ni的小数部分。由于分数延迟环节z-Di无法实现，整数阶重复控制器Gi(z)将无法准确补偿周期为非整数Ni的周期性信号，导致多重复控制器GM(z)将无法精确补偿多周期信号。为此可以采用拉格朗日插值多项式有限冲激响应（Finite Impulse Response，FIR）滤波器来逼近替代z-Di[14]：

式中：α为整数多项式阶数；Ai,q为多项式系数；q为阶数，q≠j。

一般而言，更高的多项式阶数α可使FIR 滤波器在更大带宽内更精确地逼近分数阶延迟z-Di[14]，但其实时实现的复杂性和计算耗时更高。在多数情况下，取α=3 通常就能使得式（11）在逼近精度和实现复杂性之间取得良好平衡。

将式（11）代入式（3）可得通用的分数阶多重复控制器为：

式（12）所示的分数阶多重复控制器提供了一种通用的重复控制方法来精确补偿周期性信号，譬如多周期或频率变化的信号[26]。

2 应用实例

2.1 单相PWM逆变器建模

可编程交流电源通常采用单相逆变器作为基本功能模块构件用于将电能由直流变换为交流。图2 为用于可编程交流电源的单相PWM 逆变器。

图2 中vdc为直流母线电压，vin为逆变桥后的输入电压，vo为输出电压，iL为电感电流，io为输出电流，L为输出滤波电感，C为滤波电容，R为电阻负载。图2 所示的逆变器的数学模型可表示为：

其中vin（t)=u(t)vdc(t)，而u(t) 为控制器输出到PWM 环节的控制量。

当采样周期为Ts，将式（13）离散化，在k采样周期可得：

2.2 分数阶MRC方案

逆变器控制目标是精确地生成测试所需的各种周期性交流电压。为此，本文设计开发了如图3所示的由状态反馈控制器与分数阶多重复控制器组合而成分数阶MRC 方案用于逆变器的控制。

图3 分数阶MRC方案Fig.3 Fractional-order MRC scheme

图3 中vref(k)为参考电压，u(k)为控制器输出量。根据式（14）所给出的逆变器的数学模型，可设计状态反馈控制器为：

式中：λ1,λ2,λ3为状态反馈控制器的系数。

当状态反馈控制器系数取值如下：

则vo(k+1)=vref，即只需一个采样周期延迟，输出电压vo可以跟踪参考电压vref，式（15）中的状态反馈控制器变成了无差拍控制器。无差拍控制器具备非常快的动态响应，但对模型及其参数的变化敏感，因此需要加入分数阶多重复控制器以精确跟踪参考信号。

2.3 实验验证

本文搭建了1 个3 kVA 功率的单相PWM 逆变器开展所提控制方案的实验验证工作。实验平台的系统参数如表1 所示。

表1 系统参数Table 1 System parameters

为了测试所提出的控制方案的有效性，特选取一组含有50 Hz 工频、次同步30 Hz 和超同步70 Hz的多周期参考信号vref(t)如下：

图4 显示了带有单无差拍控制器的逆变器的输出响应。

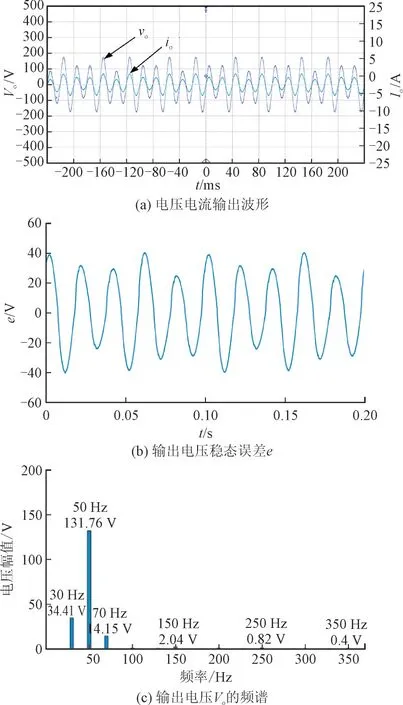
图4 单无差拍方案下实验数据Fig.4 Experimental results under deadbeat controller

图4 中波形电压vo为100 V/格、电流io为5 A/格，t为40 ms/格。其中输出电压vo由幅值为34.41 V的30 Hz 信号，幅值为131.76 V 的50 Hz 信号，幅值为14.15 V 的70 Hz 信号，幅值为2.04 V 的150 Hz信号，幅值为0.82 V 的250 Hz 信号，幅值为0.4 V的350 Hz 信号的多分量组成。输出电压跟踪误差e=vref-vo的峰值约为±40 V。150 Hz，250 Hz，350 Hz谐波分量分别是50 Hz 信号的3 次，5 次以及7 次谐波，是由单相PWM 逆变器产生的特征奇次谐波[31]。结果表明，仅用无差拍控制器不能让逆变器精确地产生指定的多周期电压。

根据图4 所示的输出电压vo的频谱特性，在无差拍控制回路中加入分数阶MRC 后GM(z)为：

其中，低通滤波器Q(z)=0.1z+0.8+0.1z-1。

为了实现快速的动态响应，选择增益总和K=0.9，控制增益ki都遵循式（8）—式（10）所提供的增益整定规则来设计。采用线性相位超前补偿器Fi(z)=zp来补偿，其中步长p=5 由实验测得。GM(z)的参数如表2 所列。其中，F1，F2，F3分别为频率为30 Hz，50 Hz 和70 Hz 对应的补偿器，[Ni+0.5]取其最接近的整数。

表2 控制器GM(z)的参数Table 2 Parameters of controller GM(z)

图5 给出了加入了分数阶MRC 的控制方案下的实验数据。图5 所示的实验结果表明，输出电压vo近乎完美地跟踪了多周期参考信号，同时从去除了不需要的3 次、5 次以及7 次谐波。结果表明，所提出的分数阶MRC 方案，能够准确地生成期望的多周期输出电压。

图5 分数阶MRC方案下实验数据Fig.5 Experimental results under fractional-order MRC

为了进一步验证分数阶MRC 方案，图6 给出了整数阶MRC 方案下的实验结果，如表2 所示，由于[Ni+0.5]和Ni之间存在一定的差值，整数阶MRC 方案不能精确产生所期望的多频信号，特别是在30 Hz和50 Hz 及其谐波，跟踪误差峰值约为±5.2 V。

图6 整数阶MRC方案下实验数据Fig.6 Experimental results under integer-order MRC

图7 显示了在空载和50 Ω 电阻负载之间的来回切换下，输出电压vo几乎没有发生显著变化。这意味着，在插入式分数阶MRC 方案下的逆变器对负载突变具有鲁棒性，并具有快速的动态响应。

图7 突然阻性负载切换下的输出响应Fig.7 Output response under sudden load changes

如图8 所示，在无差拍控制器中加入分数阶MRC 方案的逆变器，其跟踪误差的峰峰值从±40 V下降到±3.3 V，所需时间约为0.3 s，表明所提出的控制策略不仅能大大提高跟着精度，而且具有快速的响应速度。

图8 加入分数阶MRC的输出电压跟踪误差Fig.8 Output voltage tracking error with plug-in MRC

图4—图8 的实验结果表明，依据所提出的设计方法和增益调整规则设计并应用插入式分数阶MRC 方案的可编程交流电源能够取得更精确、快速和稳定的控制性能。

3 结论

本文提出了一种分数阶MRC 方案及其分析与设计方法，用于快、准、稳地补偿任意的周期性信号，尤其是含多各基波频率的多周期信号。所提控制方案由分数阶多重复控制器与状态反馈控制器优势互补组合而成，其中分数阶数字多重复控制器可为多周期信号提供稳态无差的精确补偿，而反馈控制器则提供快速动态响应和良好的鲁棒性。最后作为应用案例研究，本文将所提出的分数阶MRC方案应用于可编程交流电源的单相PWM 逆变器。实验结果表明，所提出的分数阶MRC 方案能够使可编程交流电源精确地产生所需的多周期电压，具有精度高以及响应快速等优点。