基于改进哈里斯鹰优化算法的含多能量路由器配电网多目标无功优化

从帆平，周建萍

（上海电力大学自动化工程学院，上海 200090）

0 引言

电力系统中新能源的比重不断提高，改变了电网的潮流分布，提升了电网潮流的控制难度[1-3]。因此，提升电网的潮流控制能力成为一个不可忽视的问题。柔性交流输电系统（Flexible Alternative Current Transmission System，FACTS）是指一种用于改善电力系统稳定性和可靠性的电力调节技术。它通过在交流输电线路上添加控制设备，能够实时调整电力系统的电压、电流和阻抗，优化电力系统的运行，减少电力损耗，提高电力系统的可靠性和稳定性[4-5]。因此，将FACTS 设备应用在电网的潮流控制中变得非常有必要。目前统一潮流控制器、电力电子变压器、直流潮流控制器等FACTS 设备在电网中应用比较广泛，但是这些潮流控制装置的功能比较单一，难以满足日趋复杂的电力系统。而能量路由器集多种FACTS 设备的功能为一体，因此逐渐成为近年来的研究热点[6-8]。

文献[9]研究了能量路由器在系统运行优化中的作用，结果表明能量路由器可以通过控制端口的功率注入来优化系统的运行。文献[10]建立了一种含能量路由器的配电网运行优化模型，通过仿真分析表明安装能量路由器可以有效地提升配电网的电压水平。文献[11]通过使用电能路由器，建立了一种全新的交直流混合配电网架构，经过仿真实验表明新型架构下的交直流混合配电网具有更强的供电可靠性以及更高的经济性。

电网在实际运行中，需要考虑多个优化目标，传统的单目标优化无法为电网提供最优的多目标决策方案，而基于帕累托的多目标智能优化算法可以解决此难题[12-15]。文献[16]在传统多目标教与学算法的基础上采用新的编程结构选取非支配解集，并且引入储存精英解集机制，改进后的算法获得了较好的优化效果。文献[17]基于云模型和双种群思想对遗传算法进行改进，改进后的算法具有更强的种群多样性以及更快的收敛速度。哈里斯鹰算法具备原理简单、参数较少、全局搜索能力强等优点，适合求解一些非线性程度较高的优化问题。文献[18]在全局搜索阶段引入随机云模型和随机反向学习思想，在局部开发阶段引入动态扰动策略。

本文提出一种改进的多目标哈里斯鹰优化算法（Adaptive Grid Multi-Objective Harris Hawks Optimizer，AG-MOHHO），并采用改进IEEE-33 系统进行仿真分析，以验证AG-MOHHO 算法在无功优化中的可行性和有效性。

1 能量路由器稳态潮流模型

1.1 能量路由器端口稳态模型

多端口能量路由器的拓扑结构如图1 所示[19]。由图1 可知，PSl和QSl表示能量路由器端口l与电网连接处S的有功注入功率，其中l=1,2,3,…,K,…,K+M。USl为能量路由器第l个端口的入口端交流网络节点电压幅值，δSl为能量路由器第l个端口的入口端电压相角，UCl为能量路由器第l个端口交直流连接处C端口内等效交换电压幅值，δCl为能量路由器第l个端口内的等效交换电压幅值，PCl为该能量路由器第l个端口的交/直流交换有功功率，PDl为能量路由器第l个端口直流侧D处输出的直流功率，θl为能量路由器第l个端口内等效交换直流电压滞后于入口端的交流网络节点电压的角度，IDl和UDl分别为能量路由器第l个端口的直流电流和直流电压，ISl为能量路由器第l个端口的交流电流，Rl为能量路由器第l个端口的有功功率损耗以等效电阻；XCl和XSl分别为能量路由器端口l中整流器和滤波器对于基波信号的电抗效果。

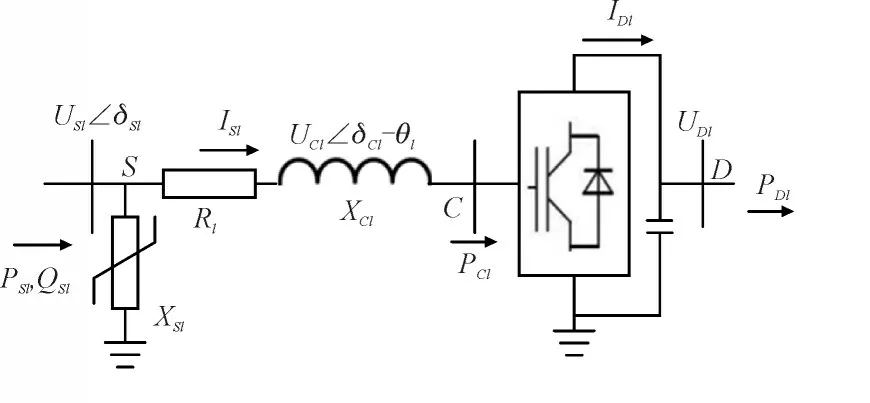
图1 电能路由器端口电力电子结构示意图Fig.1 Eletronic structure of ER ports

能量路由器端口l与电网连接处S的PSl和QSl为[20]:

式（3）可以用来描述能量路由器第l个端口的交直流连接处C端口的PCl，其中包括交流侧和直流侧之间的交换功率：

第l个端口的UCl与UDl的关系为:

式中:ml为定义的端口交直流等效电压利用控制系数；μl和Λl分别为能量路由器第l个端口的直流电压利用率和调制系数。

能量路由器中间能量交换层两侧的电压值可以通过控制电力电子器件实现。

1.2 多能量路由器稳态潮流模型

当系统中能量路由器的数量为n时，可以用集合F来标记和表示:

本文中能量路由器的端口采用PQ 控制策略。ERt表示安装在配电网中的第t个能量路由器，第t个能量路由器的第l个端口与电网连接处S的功率为，，此时能量路由器端口l节点的功率方程为[21]:

式中:为连接到ERt和外部电网连接点S的交流电压值；为ERt第l个端口内部交流节点C电压值；为第t个能量路由器的第l个端口的等效串联电导；为第t个能量路由器的第l个节点的等效串联电纳；为和两者之间的相角差；和Δ为连接到ERt和外部电网连接点S的有功和无功的偏差。

ERt的功率损耗Δ为:

式中：Ua和Ub为能量路由器一次侧和二次侧的统一端口电压；Ia和Ib为能量路由器一次侧和二次侧所有端口的电流总和；Psia和Pdyn为能量路由器中间能量交换层固态变压器的固定有功损耗和动态有功损耗。

式（7）—式（9）为ERt的潮流方程，在本例中第t个能量路由器ERt有Mt+Nt-1 个有功功率方程和Mt+Nt个无功功率方程。其中Mt为能量路由器的一次侧端口数，Nt为能量路由器ERt的二次侧端口数。在能量损失的平衡约束下，有2×(Mt+Nt)个方程是未知的，分别为Mt+Nt个相角差和Mt+Nt个电压控制系数。而第t个能量路由器松弛端口的有功功率可以通过和计算得到。

2 含多能量路由器的配电网无功优化模型

2.1 目标函数

建立了以系统有功损耗F1和电压偏离度F2最小的目标函数，具体如下:

式中：Ploss为系统有功网损；ΩD为配电网中所有线路集合；D为配电网中的总线路数；ΩN为配电网中所有节点集合；N为配电网中的总节点数；Pg1和Pg2为流过线路的有功功率；Ui为电网节点i的实际电压；Ui,min和Ui,max为节点i的电压幅值下限和上限；Uspect为电网节点额定电压。

2.2 约束条件

1）功率平衡约束为：

式中：ΔPi为第i个节点注入有功功率的不平衡量；ΔQi为第i个节点注入无功功率的不平衡量；PGi和QGi分别为发电机节点i发出的有功功率和无功功率；PDi和QDi负荷节点i消耗的有功功率和无功功率；Ui和Uj表示第i或者第j个节点的电压值；θij为线路节点i和节点j的相位差；Bij和Gij分别为交流电网中线路ij的电纳和电导；Mi为电能路由器端口-电网节点关联矩阵，其为N×K阶矩阵，元素定义如下:

对于所有的i∈SN，SN为电网节点集合。

能量路由器的中间交换层功率平衡方程式：

式中：ΔPloss为能量路由器的有功功率损耗不平衡量；Gl和Bl为电能路由器端口l的等效串联电导和等效串联电纳；δl为能量路由器端口l所连接的交流网络节点的电压相角；El为能量路由器端口l的直流侧电势；Ra和Rb为电能路由器一次侧和二次侧的端口有功损耗等效电阻；ΔPsia为电能路由器中间交换层电力电子变压器的固定损耗；对于所有的l∈Sa，Sa为能量路由器的一次端口集合;对于所有的l∈Sb，Sb为能量路由器的二次端口集合。

2）电压平衡约束为：

对于所有的l∈SN，电能路由器的一次侧和二次侧直流电压关系为:

式中：ΔUD1为能量路由器一次侧直流端D的电压差；对于l∈Sa，Sa为能量路由器的一次端口集合。

式中：ΔUD2为能量路由器二次侧直流端D电压差。

3）变量上下限约束为：

本文考虑在配电网中加入分布式电源，所以变量上下限约束为:

式中：为节点i的无功补偿容量；为节点i的无功补偿容量下限和上限；Ui,min和Ui,max为第i个节点的电压下限和上限。

4）光伏电板与风机出力上下限约束为：

式中:PVi，QVi，PWi，QWi分别为节点i所安装的光伏电板与风机的有功出力和无功出力；PV,min和PV,max为光伏电板有功功率出力下限和上限约束；QV,min和QV,max为光伏电板无功功率出力下限和上限约束；PW,min和PW,max为风机有功功率出力的下限和上限约束；QW,min和QW,max为风机无功功率出力的下限和上限约束。

3 自适应网格多目标哈里斯鹰算法

3.1 哈里斯鹰算法

哈里斯鹰算法是一种基于仿生学的优化算法，它是由哈里斯鹰捕食猎物的行为所启发而来的。该算法通过模拟哈里斯鹰捕食猎物的协同行为，来寻找优化问题的最优解。该算法的基本思想是将待优化问题转化为1 组个体，每个个体都对应1 个解空间中的可能解。通过模拟哈里斯鹰捕食猎物的协同行为，算法将个体分为2 类，即探索者和开发者。探索者负责在解空间中寻找潜在的最优解，而开发者则负责在已知最优解的基础上进行优化。具体来说，哈里斯鹰算法分为探索阶段和开发行为2 个阶段。

3.1.1 探索阶段

在探索阶段，哈里斯鹰算法通过群体智能的方式进行全局搜索。这个阶段主要的特点是随机性和探索性。在这个阶段，哈里斯鹰算法使用一种基于竞争的机制来进行个体的选择。它的基本思想是通过个体之间相互竞争寻找最优的解。探索阶段的位置更新公式为：

式中：X(t+1)和X(t)分别为第t+1 次和第t次迭代时哈里斯鹰的位置；Xrand(t)为第t次迭代时随机哈里斯鹰的位置；r1—r4和q为[0，1]区间内均匀分布随机数；Xrabbit(t+1)和Xm(t)为猎物兔子位置（当前迭代最优值）和哈里斯鹰群中心位置；ub和lb为哈里斯鹰所在位置取值范围的上下界。

其中E随迭代递减为：

式中：T为最大迭代次数；E0为初始化能量值，取[-1,1]均匀分布随机数。

3.1.2 开发行为

在开发行为阶段，哈里斯鹰算法会对前一阶段选出来的一些较优解进行进一步的优化。这个阶段的特点是确定性和利用性。在这个阶段，哈里斯鹰算法使用一种基于协作的机制来进行个体的选择。它的基本思想是，个体之间相互协作，共同优化最优解。在这个过程中，哈里斯鹰算法使用了4种不同的策略来进行搜索，分别是：

策略1：侦察。侦察是指随机生成新的解并计算其适应度，以寻找新的潜在解。哈里斯鹰算法的侦查策略为：

式中:J为猎物跳跃强度；

策略2：转移。转移是指通过对优秀解的学习和借鉴来改善当前解的策略。哈里斯鹰算法的转移策略为：

策略3：随机游走。随机游走是指通过随机生成的步长来探索解空间的策略。该算法的随机游走策略模式见式（24）和式（25）：

式中：S为随机向量；D为问题维度；LF为按文献[22]定义的Levy 飞行函数。

策略4：局部搜索。哈里斯鹰算法的局部搜索是指在当前解的附近区域进行搜索的策略。策略模式为：

3.2 改进哈里斯鹰算法

Tent 混沌映射是一种非线性、混沌的动态系统，具有良好的随机性和无序性，因此在初始化种群时可以利用这种随机性来避免算法陷入局部最优解。因此，本文将利用Tent 映射初始化种群。

Tent 映射表达式：

式中：u为系统参数；xi为系统初始值。

本文引用Tent 的混沌映射公式为：

3.3 Pareto最优解集

在多目标优化问题中，一个解的优劣通常不是单一的，需要同时考虑多个目标函数。而Pareto 最优解集是指在所有目标函数上都达到最优的解集合，其中每个解都在至少一个目标函数上优于其他解，但在其他目标函数上可能会劣于其他解。

找到Pareto 最优解集的过程通常是通过多次评估候选解来完成的。在每次评估中，多目标优化算法会根据评估结果确定当前解的支配关系，并根据支配关系更新候选解的集合。如果当前解不被其他解支配，则将其添加到Pareto 最优解集中。通过反复执行这个过程，多目标优化算法能够找到1组Pareto 最优解，这些解可以为决策者提供一个权衡不同目标之间的决策方案。

3.4 自适应网格的构建

适应网格是指在解空间中建立的一个二维网格，用于划分和组织解空间。在AG-MOHHO 算法中，自适应网格的大小和位置是根据当前粒子的位置动态调整的，以更好地适应当前解空间的特征和分布情况[23]。

具体来说，自适应网格的划分过程如下：

1）初始化网格：在初始时，将解空间划分为一个初始的二维网格，并将每个网格标记为未被访问。

2）粒子位置映射到网格：将每个粒子的位置映射到最近的网格点上，并标记该网格已被访问。

3）网格更新：根据当前已访问的网格点，动态地调整网格的大小和位置，以更好地适应当前解空间的特征和分布情况。

4）粒子移动：粒子在搜索空间中移动时，将其位置映射到最近的网格点上，并在相邻的网格点中搜索更优的解决方案。

3.5 AG-MOHHO算法的无功优化流程

AG-MOHHO 算法的求解步骤如下：

步骤1：定义无功优化问题的目标函数和约束条件。

步骤2：初始化AG-MOHHO 算法的参数，包括个体数、迭代次数、逃逸能量等。

步骤3：初始化哈里斯鹰个体的位置和速度。

步骤4：根据目标函数和约束条件更新哈里斯鹰个体的位置和速度。AG-MOHHO 算法中的位置和速度更新公式见3.1 节。

步骤5：对于更新后的哈里斯鹰个体位置，进行约束处理。如果某个个体的位置不符合约束条件，则需要对其位置进行调整。

步骤6：划分和组织解空间。在无功优化问题中，自适应网格用于划分和组织解空间。每个哈里斯鹰个体的位置映射到最近的网格点上，并标记该网格已被访问。如果某个个体的位置不符合约束条件，则将其标记的网格标记为无效。根据个体位置的分布情况，动态调整自适应网格的大小和分辨率。将个体划分到网格中后，可以计算每个网格内个体的平均适应值，并选择具有最优适应值的网格作为当前网格最优位置。将当前网格最优位置与全局最优位置进行比较，更新全局最优位置。最后，根据全局最优位置计算优化问题的解。

4 算例分析

为了验证本文所提算法和模型的有效性，利用改进的IEEE-33 系统进行仿真分析，算例接线图如图2。

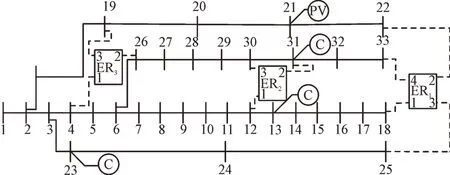
图2 含多能量路由器的IEEE-33节点系统Fig.2 IEEE-33 node system with energy router

IEEE-33 节点系统总负荷为10+16.03j MVA，电压的基准值为12.66 kV，各节点初始电压为1.00 p.u.。将ER1安装在配电网末端18，33，22，25 节点；ER2安装在12，30，31 节点；ER3安装在4，19，26 节点；在节点23 和节点31 处安装无功补偿装置；将光伏电板安装在21 节点；将风力发电机组安装在13 节点。图2 中PV 表示光伏电板，WT 表示风力机组，C 表示电容器组。

光伏电板和风力机组的输出功率如图3 和图4所示。

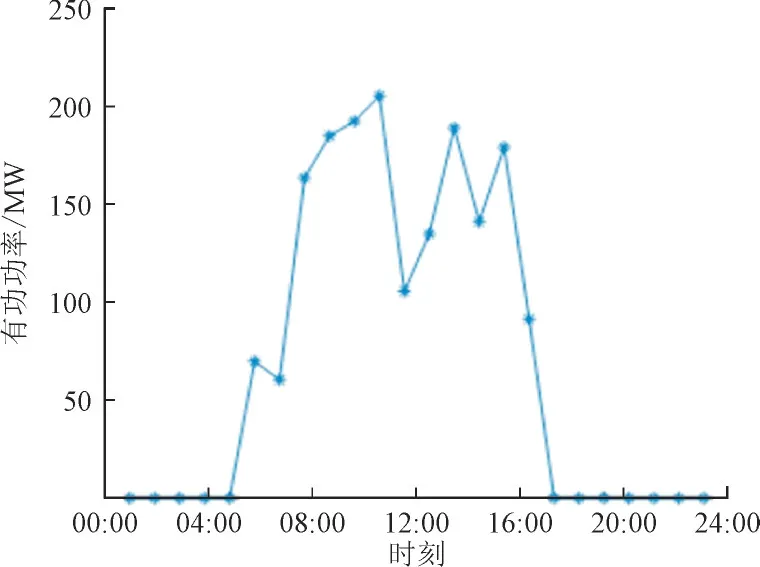
图3 光伏出力曲线Fig.3 Output curve of photovoltaic

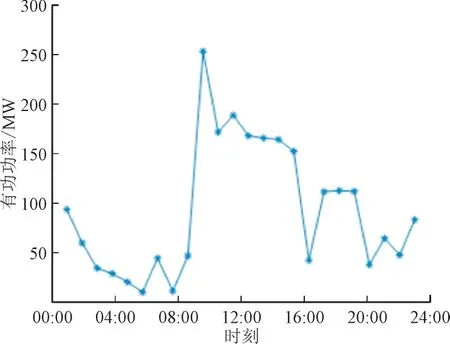
图4 风力发电曲线Fig.4 Generation curve of wind power

4.1 不同模型下的对比分析

采用AG-MOHHO 算法对3 种不同的无功优化模型进行求解和对比分析。

模型1：本文所采用的含多能量路由器的配电网无功优化模型。

模型2：含单能量路由器的配电网无功优化模型。

模型3：不含能量路由器的传统配电网无功优化模型模型。

对模型1、模型2 和模型3 的配电网进行潮流计算，得到各个节点电压如图5 所示。结果表明，相比于传统配电网，安装能量路由器以后可以有效地提升电网的电压水平，并且安装多个能量路由器的效果更佳。

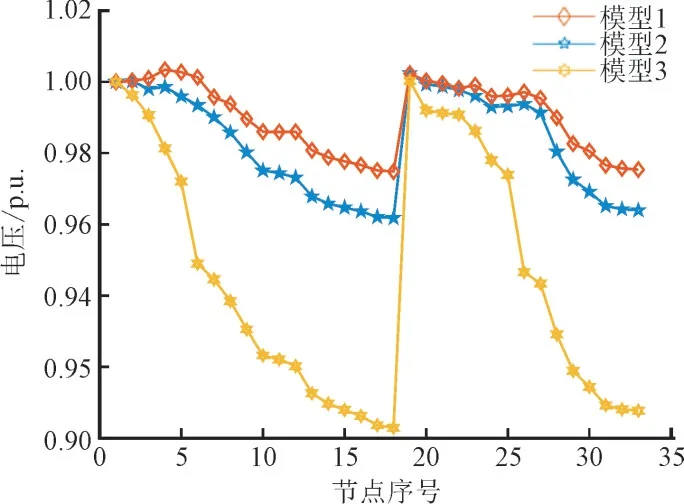
图5 不同模型下的节点电压Fig.5 Node voltage of different Models

利用AG-MOHHO 算法分别对3 种无功优化模型进行求解，优化后的能量路由器端口参数如图6所示，图6 中PS1，PS2和PS3为能量路由器3 个端口的有功功率，QS1，QS2，QS3和QS4是能量路由器的4个端口的无功功率。

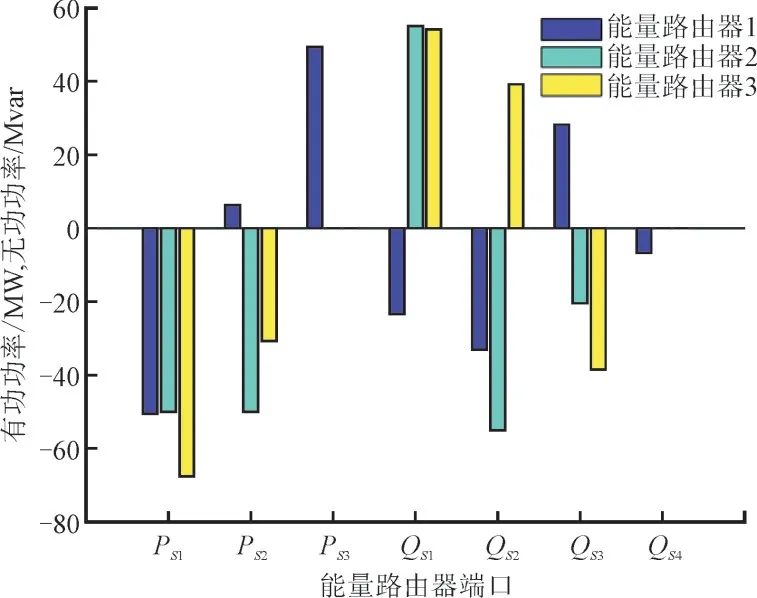
图6 优化后能量路由器端口参数Fig.6 EER’s port parameters after optimization

各模型优化后的有功网损如图7 所示。结果表明，安装能量路由器后，可以有效降低配电网的有功损耗，并且安装多能量路由器后的优化效果更好。

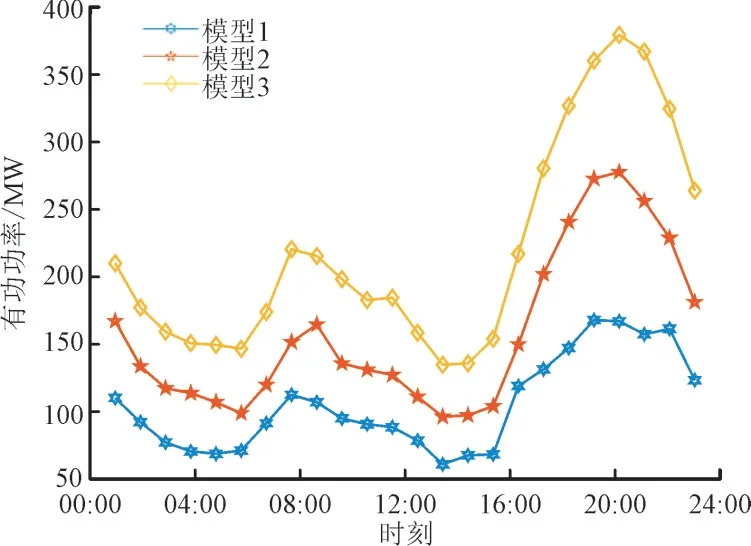
图7 不同模型下的有功损耗Fig.7 Active loss of different model

此外，3 种模型下的配电网电压偏离度变化情况如图8 所示。结果表明，模型1 和模型2 都可以有效降低配电网的电压偏离度。但是模型1 的配电网电压偏离度在大部分时刻都要低于模型2，说明本文所提方法在提高配电网稳定性方面的能力更强。

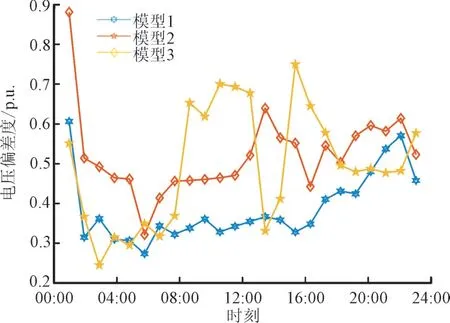
图8 不同模型下的电压偏离度Fig.8 Voltage deviation of different model

4.2 不同算法下的仿真对比分析

使用多种智能算法对含有多能量路由器的无功优化模型进行求解和比较分析，得到的Pareto 最优解集如图9 所示。图9 中MOPSO 为多目标粒子群算法（Multiple Objective Particle Swarm Optimization，MOPSO），NSGA-II 为非支配排序遗传算法（Non-dominated Sorted Genetic Algorithm-Ⅱ）。结果表明，AG-MOHHO 算法在有功网损最小值和电压偏离度最小2 个维度，均优于其他算法。

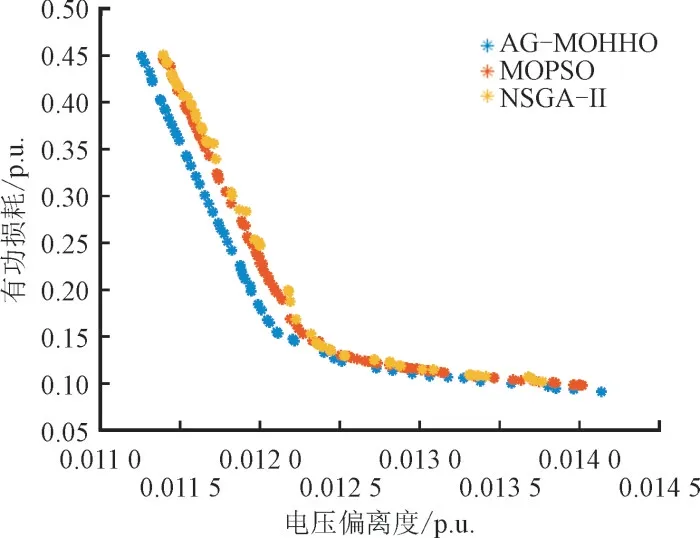
图9 IEEE-33 节点系统的Pareto 最优解集Fig.9 Pareto optimal solution set of IEEE-33 system

使用改进的多目标哈里斯鹰算法、MOPSO 和NSGA-II 求解含多能量路由器的配电网无功优化模型，计算结果如图10 和图11 所示。

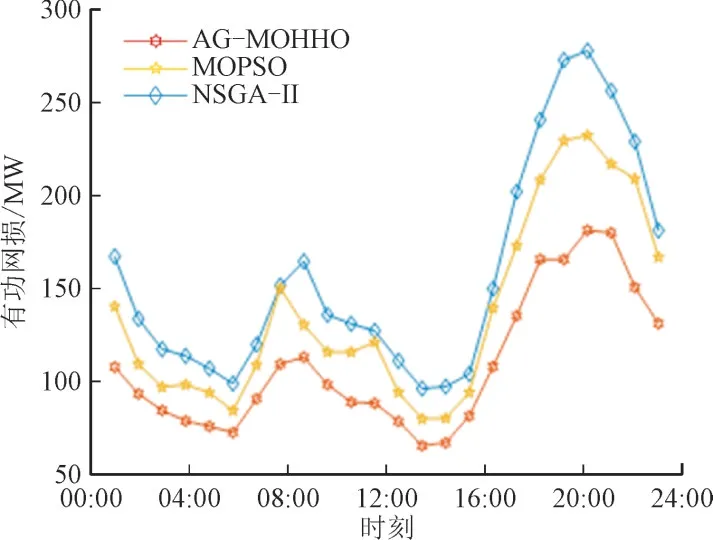
图10 不同算法下的有功损耗Fig.10 Active loss of different algorithm

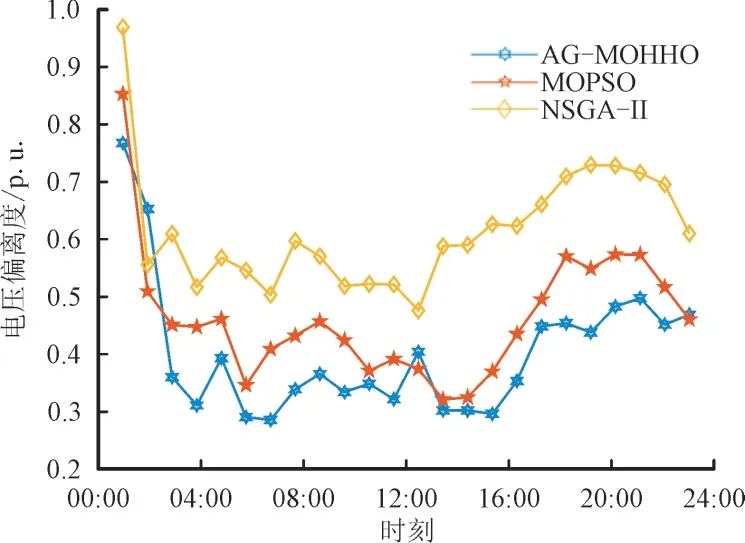
图11 不同算法下的电压偏离度Fig.11 Voltage deviation of different algorithm

以12 h 为例，AG-MOHHO 算法求解所得的有功损耗比其他2 种算法分别低22.1%和19.8%，该算法求解所得的电压偏离度比其他2 种算法分别低18.6%和17.5%。说明本文所提算法在求解配电网无功优化问题时有较好的收敛性。

5 结论

针对配电网中含有多个能量路由器的情况，本文建立了一种多目标无功优化模型，旨在最小化有功网损和电压偏离度。最后采用AG-MOHHO 算法对该模型进行了仿真验证，主要结论如下：

1）本文提出的含多能量路由器配电网无功优化模型可以显著提高配电网络的电压稳定性，同时降低配电网络的有功损耗。而且，该模型的效果优于配备单能量路由器的配电网模型和传统的配电网模型。

2）本文所提的AG-MOHHO 算法具有很好的收敛效果，其收敛精度要优于MOPSO 算法和NSGA-II。