基于GRU-BLS的超短期光伏发电功率预测

史加荣，殷 诏

（西安建筑科技大学理学院，陕西西安 710055）

0 引言

随着传统化石能源的日益紧缺和环境污染问题的日益严重，清洁可再生能源，特别是太阳能得到了大规模的开发和利用[1-2]。然而，光伏输出功率的波动性和随机性给光伏并网和电力调度带来了困难，且对电力系统的安全性和稳定性也是一种威胁[3-8]。

精确的超短期光伏功率预测是确保安全、稳定和经济的重要解决方案。因此，在1h 或更短的时间内获得精确的光伏功率预测，将有助于电网部门确定必要的备用发电容量，对促进光伏电站融入电力系统、提高电网的安全性和稳定性具有重要意义[9-10]。

为了提高太阳能发电功率的预测精度，人们提出并验证了许多预测方法[11-17]。现有的光伏发电预测模型主要将环境因素和历史数据作为输入特征变量[18-21]，再通过神经网络[22-24]等自适应学习算法对光伏发电功率进行预测。近年来，随着深度学习的发展，越来越多的混合模型被用于光伏发电功率的预测。比如Kumari 等[25]基于长短期记忆（Long and Short Term Memory，LSTM）和卷积神经网络（Convolutional Neural Network，CNN）建立了提取时空特征的混合模型，它在不同气候、季节和天气条件下均具有较好的预测精度。Tariq 等[26]将LSTM和时间卷积网络模型相结合，提出了用于光伏发电单步和多步预测的组合模型，其在不同季节和时间段都优于单一的模型。Li 等[27]建立了一种多步超前光伏功率预测的混合模型，它结合了时间序列生成对抗网络、软动态时间扭曲的中心聚类、CNN 以及门控循环单元（Gate Recurrent Units，GRU）。此外，宽度学习系统（Broad Learning System，BLS）也逐渐应用到光伏发电功率预测中，周楠等[28]基于自组织映射与BLS 构建了预测模型，它在网络宽度上扩展节点数目，并通过求解矩阵伪逆训练神经网络。李润泽等[29]采用浅层模糊宽度学习网络来预测光伏发电。

深度学习模型虽有出色的泛化能力和高的学习精度，但存在学习时间过长的问题。BLS 构建了与深度网络结构不同的宽度神经网络，虽然学习速度得到了很大的提升，但由于多隐藏层结构导致其学习精度受到影响。深度学习模型能够从训练数据中挖掘出更抽象的特征，具有很好的泛化能力，而BLS 能够从训练数据中学习到重要特征，且对训练数据拟合度较高。因此，本文将GRU 与BLS 相融合，提出GRU-BLS 模型，并将其应用于超短期光伏发电功率预测。所提出的模型可有效缓解深度学习训练时间长和易陷入局部极值的缺点，同时宽度学习拟合能力不足的问题也得以改善。

1 模型的构建

1.1 GRU模型

作为循环神经网络的变体之一，GRU 能够很好地捕捉光伏发电功率序列长短期之间的依赖关系，解决复杂因素影响下的预测问题。GRU 网络分为重置门、更新门、候选隐藏状态及隐藏状态[30]。

在第t个时刻，重置门的输入为发电功率特征向量xt∈Rd×1和上一时刻的隐藏层状态向量it-1，d为输入特征维数。重置门输出向量rt为：

式中：Wr和Ur为重置门的参数矩阵；br为重置门的偏置向量；σ为Sigmoid 函数。

更新门的输入与重置门相同，输出向量zt为：

式中：Wc和Uc为更新门的参数矩阵；bc为更新门的偏置向量。

候选隐藏状态的输入比更新门多了一项rt，输出向量为：

式中：W和U为隐藏层的参数矩阵；bh为候选隐藏状态的偏置向量；“⊙”为向量对应元素相乘；tanh为双曲正切函数。

隐藏状态将更新门输出、上一时刻隐藏状态和当前时刻候选隐藏状态进行组合，计算公式为：

记xt样本输出为yt∈Re×1，e为输出特征维数，则GRU 模型中yt的预测值为：

式中：Wo和bo分别为输出部分的连接权重矩阵和偏置向量。

与LSTM 相比，GRU 仅通过更新门和重置门实现对信息的保留和遗忘，加快样本训练速度。

1.2 BLS模型

作为一种简单的新型快速增量学习模型，BLS采用了随机向量函数连接网络[31]。它将模型结构拓宽以克服深度学习易陷入局部最优的缺点，实现训练速度和预测精度的提高。将N个时刻的发电功率特征构成矩阵X，即X=(x1,…,xN)T。建立从原始特征矩阵X到n个特征节点的映射，第k个节点的特征Tk为：

将n个特征节点组成矩阵T(n)=(T1,…,Tn)。

根据T(n)生成m个增强节点：

将所有增强节点构成矩阵H(m)=(H1,…Hm)。

令Y=(y1,…,yN)T，BLS 将映射特征T(n)和H(m)进行连接，进而对Y进行预测：

式中：W(m)为输出层的连接权重矩阵。

1.3 GRU-BLS模型

基于深度学习和宽度学习系统的优势，提出GRU-BLS 预测模型。该模型先利用GRU 提取时间序列特征，再使用BLS 进行预测，可以更好地表达光伏发电功率的非线性特性。

将输入实例xt输入到GRU 网络，训练模型参数，经式（1）至式（4）得到隐藏状态it。记I(N)=(i1,…,iN)T，将I(N)视为输入特征矩阵，根据式（6）生成n个新的特征节点：

其中‖·‖F表示矩阵的Frobenins 范数，式（12）的最优解表示为：

式中：Q+为Q的伪逆。

由于式（13）泛化误差可能较大，故考虑正则化的目标函数，即新的优化模型为：

式中：λ为惩罚项系数，λ>0。

称优化模型式（14）为岭回归问题，最优的权重矩阵为：

式中：E为单位矩阵。

所提出的GRU-BLS 模型的结构框架如图1 所示。在GRU 模块，根据输入特征矩阵X重新构造样本集的输入特征。在BLS 模块，依据所构建的特征矩阵I(N)，建立宽度学习系统，再根据输出特征训练网络模型。

1.4 预测流程

将所提出的GRU-BLS 模型用于光伏发电功率数据的预测，流程如图2 所示。

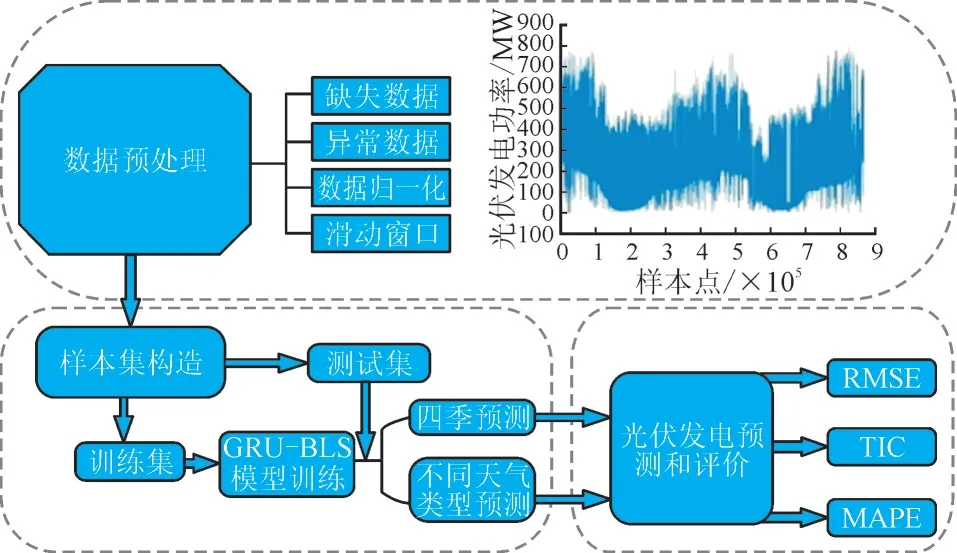
图2 光伏发电功率的GRU-BLS预测流程图Fig.2 Flow chart of GRU-BLS prediction for photovoltaic power generation

图2 中RMSE，TIC，MAPE 分别表示均方根误差（Root Mean Squared Error，RMSE）、希尔不等系数（Theil’s Inequality Coefficient，TIC）、平均绝对百分误 差（Mean Absolute Percentage Error，MAPE）。RMSE，TIC 和MAPE 的值分别用ERMS，CTI，EMAP表示。预测流程主要分为以下4 个步骤。

1）数据预处理：筛选出异常值，并用正常值进行替换；对于缺失值，利用插值方法进行恢复；将数据进行归一化处理。

2）数据集的划分：对预处理后的序列数据，根据指定的滑动窗口构造样本集，并将其分为训练集和测试集。

3）模型训练：将训练集输入到GRU 模型中进行初步训练，并构造新特征；再将这些新特征输入到BLS 中，确定最优连接权重。

4）模型评价：将所提出GRU-BLS 模型应用在光伏发电功率预测中，并考虑不同季节和天气类型下的预测结果。

2 实例分析

2.1 数据来源与预处理

本文所用数据集来自澳大利亚Yulara 光伏电站（https://dkasolarcentre.com.au/download?location=alice-springs），光伏材料为聚硅橡胶、1 058.4 kW 固定式面板。选取2018 年1 月1 日到2020 年1 月1日光伏功率稳定输出的时段（8：00—17：55），采样间隔为5 min。

为提高数据的质量以及减少噪声的影响，需要对原始数据集进行预处理。本文采用3σ原则筛选异常值：以正态分布为基础，落在正态分布3σ边界外的数值则为异常值。对缺失和异常的数据点进行标记，通过取相邻数据的平均值来代替异常值和缺失值。最后将清洗后的数据进行[0，1]区间归一化处理。

数据集共86 859 条记录，使用前6 个时刻的光伏发电功率值来预测下一时刻功率输出值，即步长d=6，输出特征维数e=1。按照时间顺序选取前80%的样本集用作训练，其余的20%用作测试。将所提出模型的预测性能与BLS，GRU，LSTM 和LSTMBLS 等几种学习方法进行比较。

2.2 参数设置和评价指标

使用网格搜索方法确定GRU-BLS 模型中的超参数。在GRU-BLS 的GRU 模块中，设置隐藏层的层数为4，各层神经元数分别为128，64，32，32；稠密层的层数为2，对应神经元数分别为10 和1；选取的损失函数为均方误差（Mean Squared Error，MSE），迭代轮数为20。在GRU-BLS 的BLS 模块中，设置映射特征节点个数n为10，增强节点个数m为280，惩罚项参数λ为10-5。对于单一的GRU或BLS 模型，超参数的设置与GRU-BLS 模型的对应模块相同。LSTM 和LSTM-BLS 2 种模型的迭代轮数均设置为20。与GRU 类似，设置LSTM 的层数为4，神经元数目分别为64，64，32 和16。在LSTM-BLS 中，BLS 模块的超参数与GRU-BLS 对应的超参数设置相同。

为了有效地评估模型的预测精度，使用ERMS，CTI，EMAP3 项指标作为依据，它们的计算公式为：

式中：yi为第i个测试样本的真实值；为第i个测试样本的预测值；Ntest为测试集样本的数量。

ERMS用来评价功率预测值与真实值之间的偏差。CTI越小表明预测精度越高，当CTI=0 时预测曲线与真实曲线完全吻合。EMAP常用于评估时间序列的预测误差，其值越小，预测精度越高。

2.3 预测结果及分析

将GRU-BLS 的预测性能与其他4 种模型进行比较，3 项评价指标如表1 所示。观察表1 可知:3种单一模型中，BLS 对数据的特征提取能力最差，这可能是因为LSTM 和GRU 保持了数据集的时序结构；组合模型LSTM-BLS 和GRU-BLS 的预测性能显著优于单一模型；与LSTM-BLS 相比，GRU-BLS的ERMS，CTI和EMAP分别改善了39.49%，11.65%和16.38%。综上所述，在不同的评价指标下，GRUBLS 模型取得了最佳的预测精度。

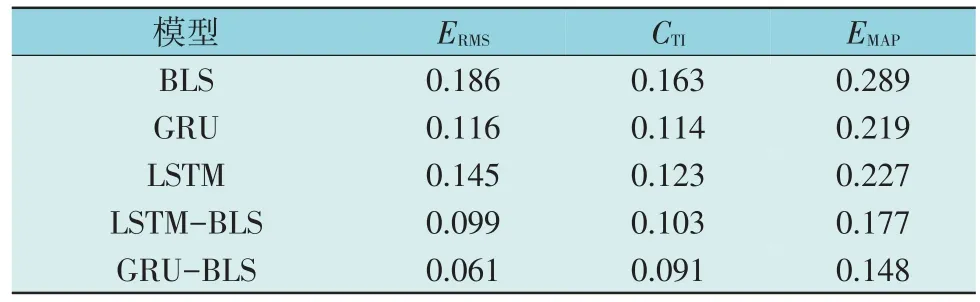
表1 各模型的预测误差对比Table 1 Comparison of prediction errors among different models

图3 绘制了各模型在部分测试集上的预测结果，此处对光伏发电功率进行了反归一化处理。

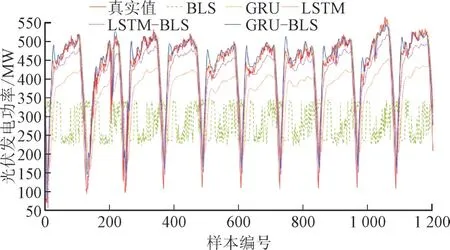
图3 各模型部分预测值与真实值比较Fig.3 Comparison between predicted values and actual values of each model

从图3 可以看出：除BLS 外，所有模型的预测曲线与原始时序曲线变化趋势均保持一致，且GRU-BLS 模型的预测结果更接近真实观测值。

2.4 模型时间效率分析

比较GRU 和GRU-BLS 2 种模型的训练时间。选取ERMS作为评估误差，时间效率的比较如图4 所示。从图4 可以看出：当GRU 模型训练时间为1 758 s 时，ERMS为0.064 3，而GRU-BLS 模型的ERMS达到0.062 1 时仅用时224 s，即相近的预测误差下所提模型GRU-BLS 具有更少的训练时间。

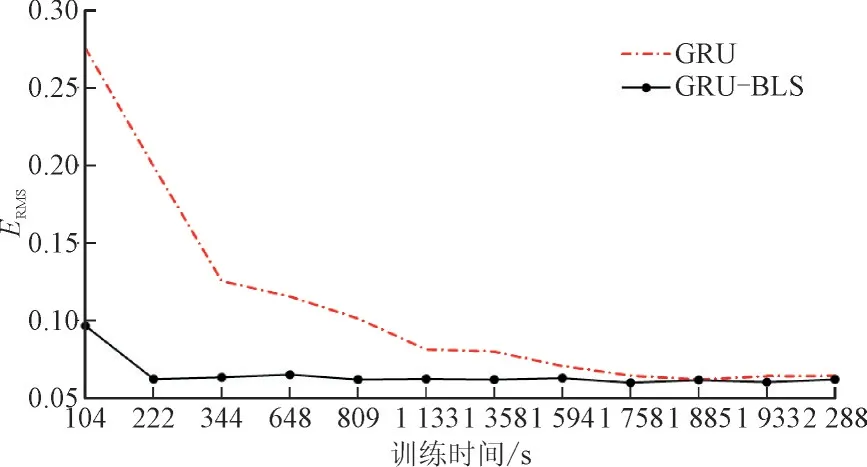
图4 GRU与GRU-BLS模型的训练时间效率对比Fig.4 Comparison of training time efficiency between GRU and GRU-BLS models

3 不同季节与类型日的算例分析

3.1 不同季节的预测

光伏发电功率与季节有很强的相关性。为了进一步说明所提出模型的有效性和优越性，另选取2020 年5 月（秋季）、6 月（冬季）、10 月（春季）、12月（夏季）的数据进行测试。图5 至图8 分别绘制了所选季节的部分预测值曲线。对比各模型的仿真结果，可得如下结论：在各季节中太阳辐射度变化导致光伏发电有间歇性，但GRU-BLS 仍然捕捉到每个季节的光伏功率变化模式，预测曲线更接近实际光伏发电功率曲线。在图5—图8 的上方绘制其方框内预测曲线和真实值曲线放大图，以便可视化预测性能对比，可知当真实光伏功率波动较大时，GRU-BLS 的预测曲线与真实值曲线几乎一致，其中秋季的预测性能最好。当真实光伏发电功率较小时，所提出的模型也能更准确预测光伏功率，其拟合度优于其它方法。

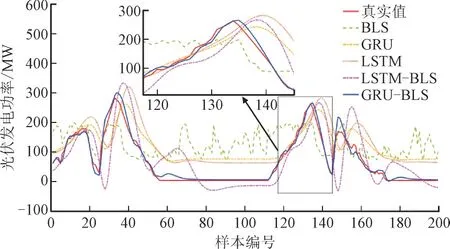
图5 秋季光伏发电功率部分预测值和真实值Fig.5 Partial predicted and actual values of photovoltaic power generation in autumn

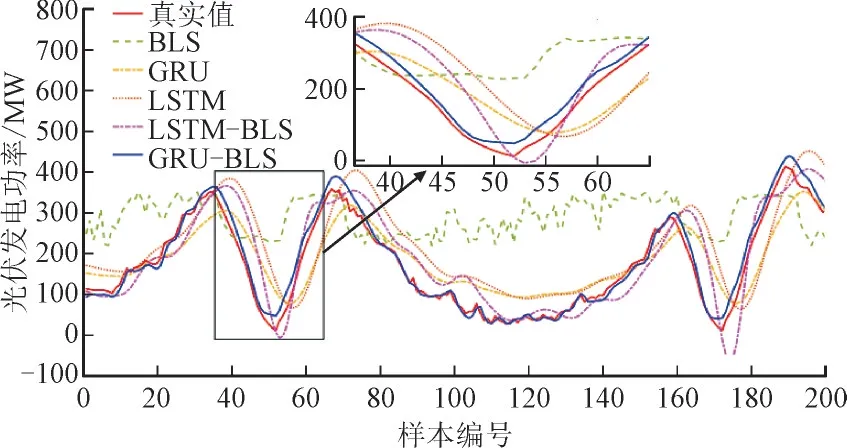
图6 冬季光伏发电功率部分预测值和真实值Fig.6 Partial predicted and actual values of photovoltaic power generation in winter

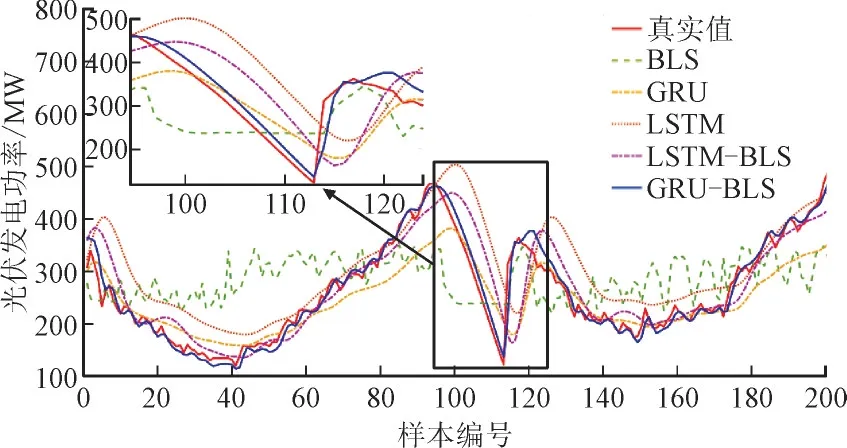
图7 春季光伏发电功率部分预测值和真实值Fig.7 Partial predicted and actual values of photovoltaic power generation in spring

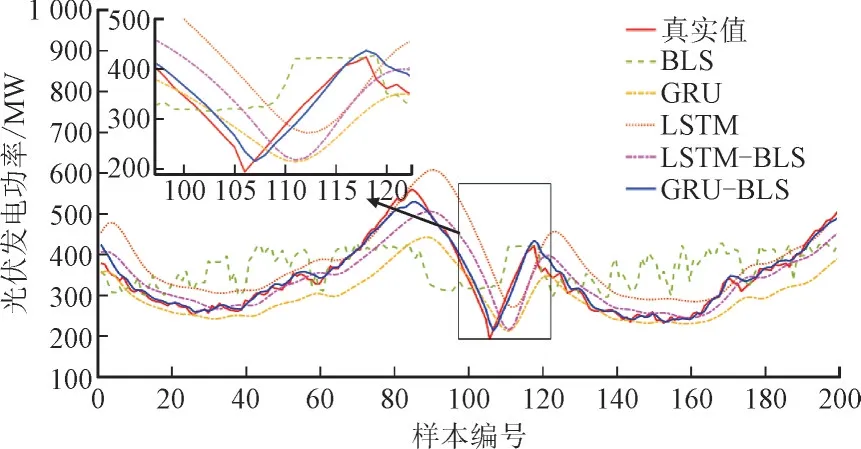
图8 夏季光伏发电功率部分预测值和真实值Fig.8 Partial predicted and actual values of photovoltaic power generation in summer

表2 给出了不同季节下5 种模型的预测评价指标。观察表2 可以发现：所有模型在秋冬2 季的评价指标比较好，这是因为当地3 月到8 月晴天多、雨天少，阳光强度高；而春夏两季暴雨多，气候湿度大，从而导致太阳辐射的不确定性和不稳定性愈加严重。在春季，所提模型的ERMS比BLS，LSTM，GRU，LSTM-BLS 分别低55.21%，45.57%，33.84%，36.4%，CTI分别低70.63%，50.82%，41%，40.07%，EMAP值分别低77.02%，66.45%，66.22%，48.79%。在秋季，GRU-BLS 的ERMS比其它4 种方法分别低75.68%，57.09%，44.4%，37.76%，CTI分别低66.12%，33.09%，44.06%，26.18%，EMAP分别低71.57%，35.27%，54.21%，32.42%。此外，在夏冬季节，所提模型也取得了最优性能。总之，GRU-BLS 模型在各季节的评价指标值均为最低，预测效果显著优于其它模型。

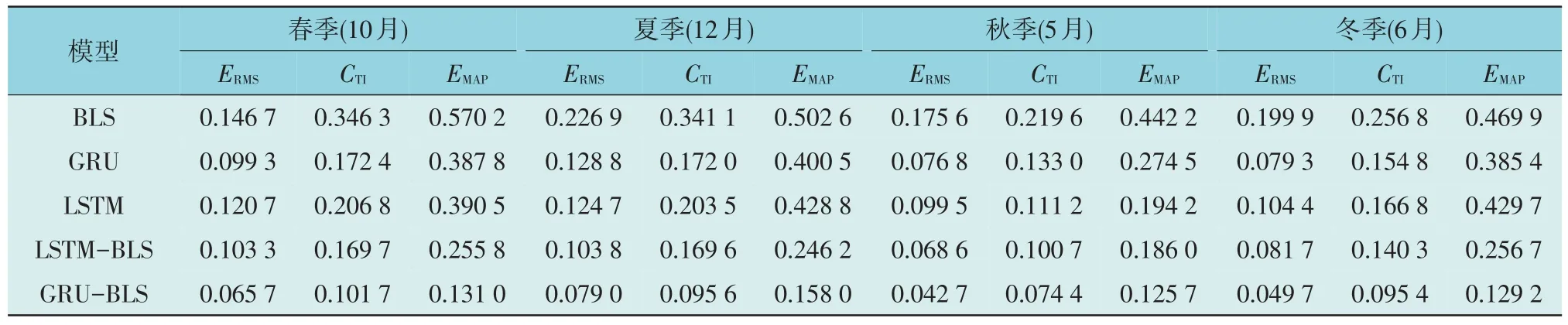
表2 不同季节下5种模型的预测性能Table 2 Prediction performance of 5 models under different seasons

这些观测结果进一步表明：无论太阳辐射波动是否强烈，在相同条件下GRU-BLS 具有最优的性能。综上所述，GRU-BLS 能有效地从数据中提取特征、捕获信息和学习模式。此外，所提模型在不同季节都表现出良好的性能，适用于一年中的所有季节。

3.2 不同天气类型的预测

为了更深入地说明所提出模型的优越性，考虑3 种不同的天气类型：晴天（辐射稳定）、雨雪天（PV功率低）和间歇日（辐射变化大），并对它们的功率进行预测。

图9 至图11 给出了所提模型在3 种典型天气日8：00—17：35 的预测光伏功率曲线。通过观察图9 至图11，可以看出：在晴天，GRU-BLS 能精确捕捉小幅度光伏功率变化，其预测曲线几乎与真实值重合；在雨雪天，GRU-BLS 虽不及晴天预测性能，但也能在光伏功率大幅度波动时逼近真实曲线；在间歇日，GRUBLS 预测曲线在少数时刻并不能准确预测光伏功率，但整体上预测曲线变化趋势与真实值大致相同。

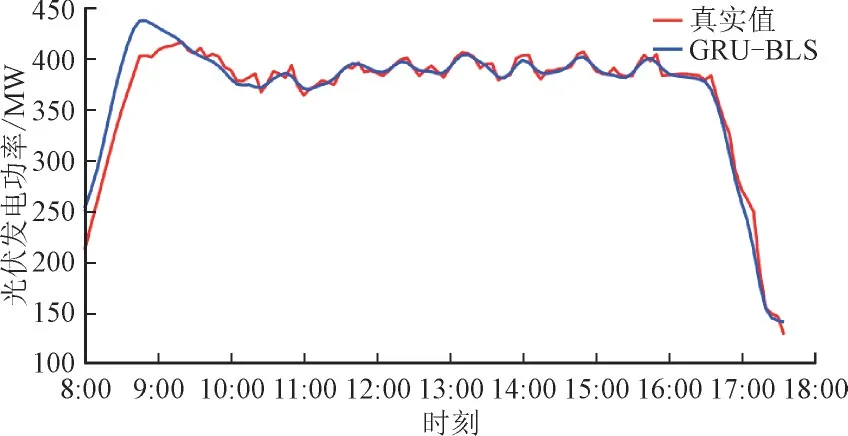
图9 晴天GRU-BLS光伏发电功率预测值和真实值Fig.9 Predicted and actual values of GRU-BLS photovoltaic power generation on clear days

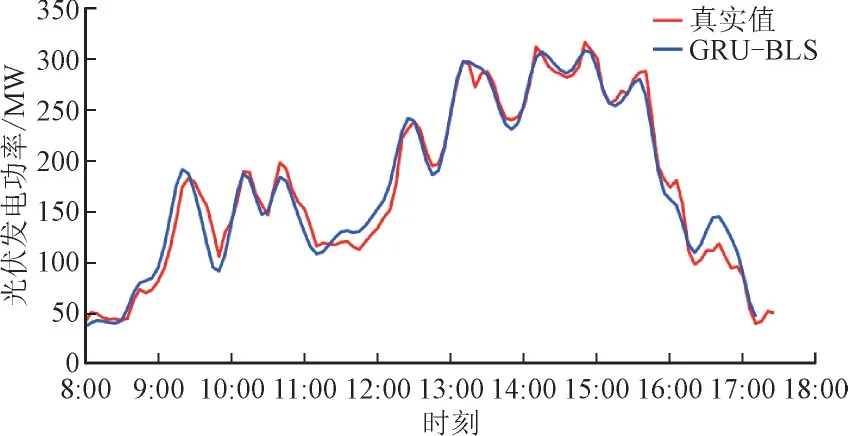
图10 雨雪天GRU-BLS光伏发电功率预测值和真实值Fig.10 Predicted and actual values of GRU-BLS photovoltaic power generation on rainy and snowy days

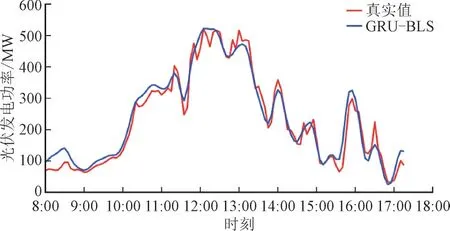
图11 间歇日GRU-BLS光伏发电功率预测值和真实值Fig.11 Predicted and actual values of GRU-BLS photovoltaic power generation on intermittent days

表3 展示了各模型的预测误差评价指标，可以得出如下结论：以ERMS为例，GRU-BLS 在晴天比LSTM，BLS，GRU，LSTM-BLS 分别低86.17%，85.29%，76.29%，46.8%；在雨雪天的误差分别低71.18%，79.58%，58.56%，39.72%；在间歇日的误差分别低62.09%，63.46%，45.75%，39.15%。在3 种天气类型下，GRU-BLS 在晴天时的预测误差最小。在雨雪天类型下，太阳辐射的不确定性和随机性均增高，各模型都无法非常精确地预测。在间歇日类型下，太阳辐照强度产生剧烈变化，光伏功率波动较大，各个模型预测偏差较大。

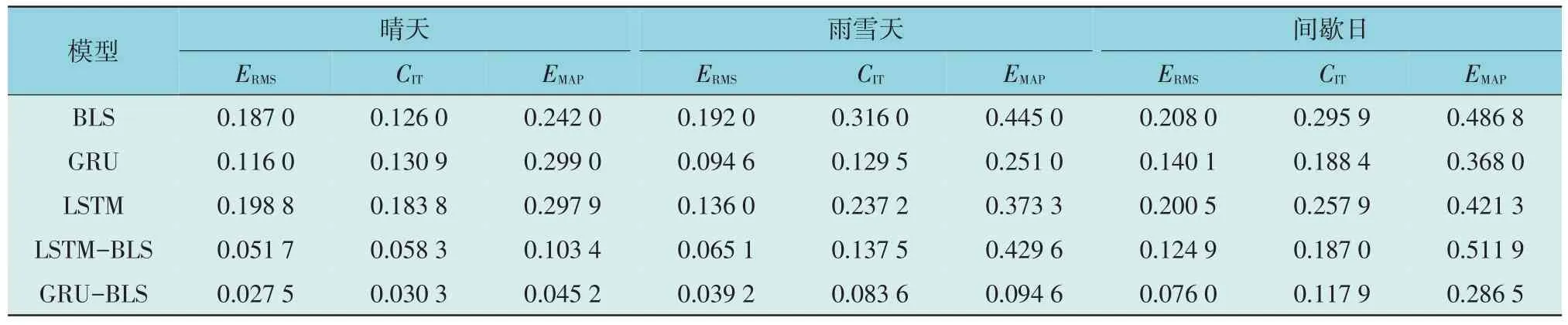
表3 不同类型日5种模型的误差值Table 3 Error values of 5 models for different types of days

由各模型在不同天气类型下的评价指标值和仿真结果可知：无论在光伏功率稳定输出的晴天还是波动较大的突变天气，本文所提出的GRU-BLS模型的预测曲线与实际光伏发电功率曲线高度拟合，预测误差均显著低于其它模型。

4 结语

为了提高超短期光伏发电功率的预测精度和运行效率，提出了GRU-BLS 模型。首先利用GRU网络从输入数据中提取时间特征；然后根据GRU学习到的隐特征，构造BLS 的特征节点和增强节点，从而得到最终的特征表示。与传统的BLS 模型相比，所提模型中的特征节点的输入是由GRU 学习得到的隐特征，因此提高了BLS 的预测精度，同时减少了GRU 的训练时间。实验结果验证了GRU-BLS 显著优于其它模型。此外，还探讨了所提模型在不同季节和特定的天气条件（晴天、雨雪天和间歇性天气）下的预测性能，以及对比了GRU 网络与GRU-BLS 模型的运行效率。总之，本文提出的混合模型在保留GRU 网络高精度的同时，还保留了BLS 运行速度快的优点。

本文研究内容侧重于光伏发电自身的历史功率数据，未考虑温度、风向和太阳辐射等影响因素，也未探讨多步预测，这些问题值得进一步研究。在今后的光伏功率预测的探索中，还可以考虑加入模态分解，以削弱预测模型中数据波动的影响，使宽度学习能增强数据的特征提取能力；设计智能算法，优化所建模型的超参数，以进一步提高预测能力。