基于多源数据的电动汽车充电设施布局优化方法研究

姚 明，毛文杰，曹淑超，笪丹宁

（江苏大学汽车与交通工程学院，江苏镇江 212013）

0 引言

近年来，电动汽车数量增长迅猛，发展前景广阔。电动汽车的规模化应用将引发总量庞大的充电需求[1-3]。电力需求的急剧增长将影响电力基础设施和能源系统的规划和运行[4-6]。因此，电动汽车充电站布局优化成为研究的一个重要问题。文献[7]以插电式混合动力汽车由公共区域、目的地、行驶路线之间的相互作用为基础搭建了均衡建模框架。文献[8]通过评估电动汽车在现实驾驶环境中异质旅行人群的可行性，来确定充电站选址的最佳位置。文献[9]以居民负荷的分布情况为基础，以投资运营收益最大化为目标构建选址模型。文献[10]在预测电动汽车保有量基础上建立选址模型。文献[11-12]基于充电需求量来确定充电站的最佳位置。文献[13]以覆盖率、重合度、充电功率为构建选址模型的约束条件。文献[14]以路网补能负效应最小化为目标，建立电动汽车补能诱导双层优化模型。文献[15]提出的终端预防模型可以在不同情况下建造充电站。文献[16-17]以充电站布局总成本最小为目标函数搭建选址定容模型，并对影响因素进行灵敏度分析。文献[18]基于已有充电站和新建充电站之间的关系，并考虑投资成本与充电距离构建选址模型。文献[19]以通过GPS 获得的电动出租车运行轨迹为基础，确定出租车充电桩选址方案。文献[20-21]利用Voronoi 确定备选充电站服务范围，增加优化算法的宣发寻优效果，进一步优化选址定容效果。文献[22]从用户和政府角度出发构建双层模型，提出一种耦合改进多目标算法NSGA-Ⅱ，TOPSIS（Technique for Order Preference by Similarity to Ideal Solution），Floyd 算法的求解框架。

综合现有的电动汽车充电站布局优化研究在构建模型时通常以距离用户最近的充电站为目标电站，忽略了寻址时间、排队时间等因素对布局优化结果的影响，且没有考虑每个用户的具体需求。为此，本文基于用户产生充电需求时的地点、需求偏好等多源数据，建立了双层电动汽车充电站布局优化模型，上层模型为社会总成本最小化的充电设施选址定容模型，下层模型为满足用户具体需求的用户最佳选择模型，并通过改进遗传算法求解得到电动汽车充电站布局优化方案。

1 电动汽车充电站布局优化模型

1.1 用户最佳选择模型

电动汽车充电设施布局规划必须考虑用户的选择偏好及用户的寻址、排队、充电过程，这些过程受寻址时间、寻址距离、拥挤程度的影响。因此，本文在考虑整体用户寻址充电便利度的同时兼顾每个用户的具体需求，建立用户最佳选择模型，其目标函数为：

图1 用户最佳选择模型求解流程图Fig.1 Flow chart of solving user optimal choice model

1.2 电动汽车充电站选址定容模型

综合考虑电动汽车充电站投资经营者与用户的利益，以社会总成本最小为目标函数构建电动汽车充电站布局优化模型，其表达式为：

式中：F为充电设施运行至目标年限的社会总运行成本：F1为充电设施运行至目标年限的建设运营成本；F2为用户行驶至充电设施的距离年损失成本；F3为用户行驶至充电设施的时间年损失成本；F4为用户排队年损失成本；F5为惩罚函数。

1）电动汽车充电站建设运营成本。电动汽车充电站的建设成本主要包括地皮成本、充电桩成本及与充电桩总额定功率有关的成本。其中，不同等级充电站的储存能量、充电桩数量、服务能力、基础建造成本、运营成本均不相同。因此，第j座电动汽车充电站的建设成本为：

式中：r为折旧率；m为充电设施运营年限；ϕ为电动汽车充电站内相关建筑设施、辅助设施、道路、绿化及其他设施占地面积折算到车位面积的比例系数；Sj为j候选电站快慢桩单个桩占地面积；Gj为j候选电站单位土地价格；Sjkc为j候选电站快充充电桩数量；Gkc为快充充电桩单价；Sjmc为j候选电站慢充充电桩数量；Gmc为慢充充电桩单价；Jj为j候选电站的基础建造成本，包括购买配电变压器、有源滤波装置、电缆等设施的成本；Rj为j候选电站的运营成本；hj为决策变量；M为候选电站数量。

2）用户行驶距离年损失成本。用户的行驶年损失成本主要包括用户行驶至电动汽车充电站途中产生的时间成本与耗电量成本，则用户的年损失成本为：

式中：Lij为用户i到候选电站j的距离；λ为城市道路曲折系数；Qi为用户i电动汽车的每公里耗电；Ej为j候选电站的单位电价；xij为决策变量；N为用户数量。

3）用户行驶时间年损失成本。

式中：Gi为调查区域内用户单位时间成本（本文以2021 年中国人均小时GDP 为单位时间成本）；Ti为用户i的行驶时间。

4）用户排队年损失成本。用户排队年损失成本主要由用户到达电动汽车充电站后在充电前产生的排队时间成本，第j座电动汽车充电站服务范围内用户的年损失成本为:

式中：Pi为用户i非行驶状态下每小时耗电量；

5）惩罚函数。本文假设用户均充电至100%电量时结束充电。惩罚函数是为去除用户行驶距离超过当前电量所能支持的最远行驶距离的方案。

式中：Zi为用户i电动汽车电池容量；α为产生充电需求时的电池容量系数，电动汽车剩余电量在低于30%电池电量时强制电动汽车充电[24]，因此本文将α设为30%；H为惩罚因子。

1.3 约束条件

在解决充电站布局优化目标函数的最小化问题时，应考虑以下约束：

1）决策变量约束见式（11）—式（15）。其中，式（11）表示用户每次只能前往1个候选充电站进行充电；式（12）表示每次只能在候选充电站中选择方案确定的充电站；式（13）—式（14）表示决策变量范围；式（15）表示只有在候选电站建造充电设施的情况下，用户i才能去进行充电；

2）充电站约束见式（16）—式（18）。其中，式（16）表示选择候选电站的服务容量限制。考虑目标区域内各候选电站的公共停车位数量有限，本文在1 个充电站内的快慢充电桩总数最大值为60；式（17）—式（18）表示目标区域内电动汽车充电站数量约束。

式中：ne为充电站数量；分别为充电站数量上、下限；need为目标区域内每天的总需求数量；Smin，Smax分别为电动汽车充电站最小、最大容量限制。

3）用户约束见式（19）—式（20）。其中，式（19）表示需求点到候选电站的最远距离限制;式（20）表示用户分配权重约束；

式中：Lmax为用户当前电量所能支持的最远行驶距离。

2 模型求解

2.1 模型求解策略

电动汽车充电站布局优化规划是一个含多约束条件的多目标优化问题[25-26]，本文在选址遗传算法中加入定容遗传算法对电动汽车充电站布局优化模型进行求解，求解结果更精准，迭代过程更灵活。本文所提出的双层遗传算法求解流程如图2 所示。

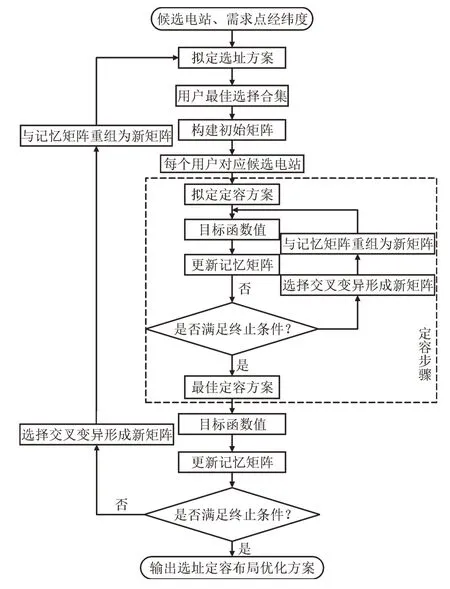
图2 电动汽车充电站布局优化算法流程Fig.2 Optimization algorithm flow of EV charging station layout

主要求解流程为：（1）基于java 爬虫，借助高德web 服务应用程序编程接口（Application Programming Interface，API）获得目标区域内兴趣点（Point of interesting，POI）分布。使用K-MEANS 聚类算法将POI 数据进行聚类，将获得的聚类中心确定为需求点；（2）求解用户最佳选择模型，获得每个用户的最佳选择合集。生成初始选址方案，选址方案中每个用户对应的候选电站在各自的最佳选择合集中生成；在上层传统遗传算法中插入下层定容遗传算法，获得不同选址方案下的最佳定容方案，并以此作为参数计算目标函数值；（3）计算选址目标函数值并更新记忆矩阵，判断是否满足终止条件。如满足，则输出最优解；若不满足，则进行选择交叉变异步骤形成新矩阵并与记忆矩阵重组成新种群并返回步骤（2）。

2.2 数据获取

本文对某占地面积为124.68 km2的区域内的电动汽车充电站进行规划。目标区域内POI 数量共计2 117 个，对数据进行聚类，得到聚类中心。根据充电站和换电站的建设选址原则[10]选取的候选站点均为公共停车场且分布在各聚类区域内，具体分布情况见图3。与布局优化模型相关的参数设置见表1；规划区域内电动汽车充电站的不同等级1，2，3，4及相应成本规定[27]见表2。

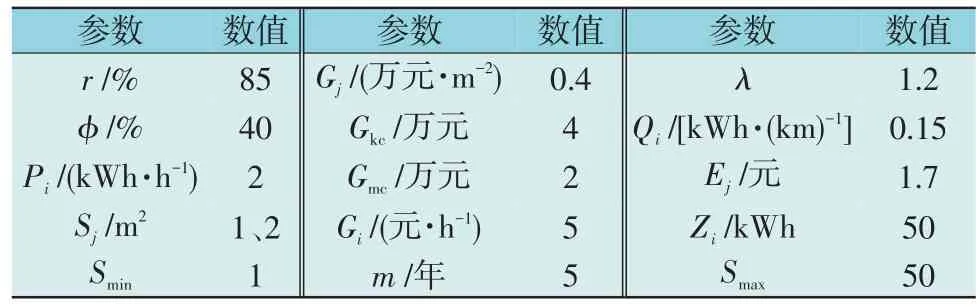
表1 电动汽车充电站布局相关参数Table 1 Optimization parameters of EV charging station layout

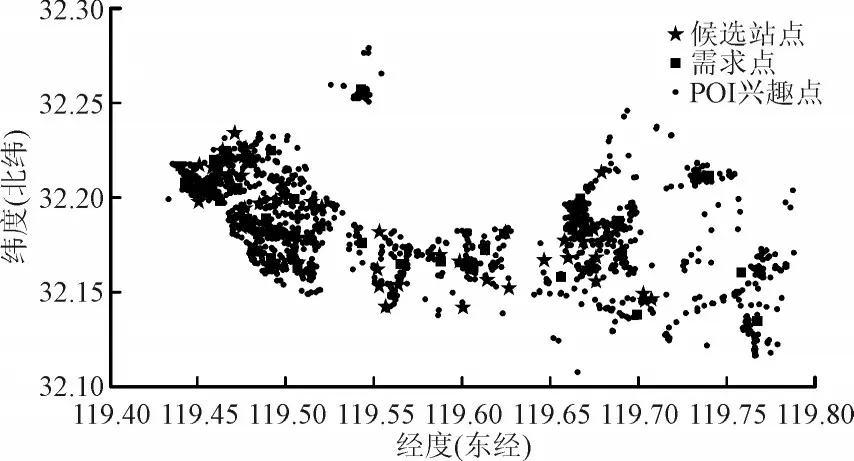
图3 需求点、候选电站分布情况Fig.3 Distribution of demand points and candidate power stations

3 实例验证

3.1 不同用户选择偏好下的成本分析

本文提出的电动汽车充电站布局优化方法是以每个用户的最佳选择合集为基础，用户对寻址时间、寻址距离、拥挤程度3 个指标的权重划分将直接影响最终的布局优化结果。因此，对不同用户选择偏好下的模型进行求解。首先将θ1，θ2，θ3按取值大小排序，假设分别为θmax，θse，θth。θmax数值确定后，θse，θth分配剩下的1-θmax值。设置所有用户的权重划分一致，计算θmax分别对应寻址时间、寻址距离、拥挤程度时的布局优化结果，进行对比分析。

当θmax取值确定后，设所有θse，θth分配情况共n种，θmax对应时间成本、距离成本、排队成本的计算公式分别为：

分别计算θmax取0.6～0.9 时的布局优化结果，用户权重的变化对各成本的影响如图4—图6 所示。

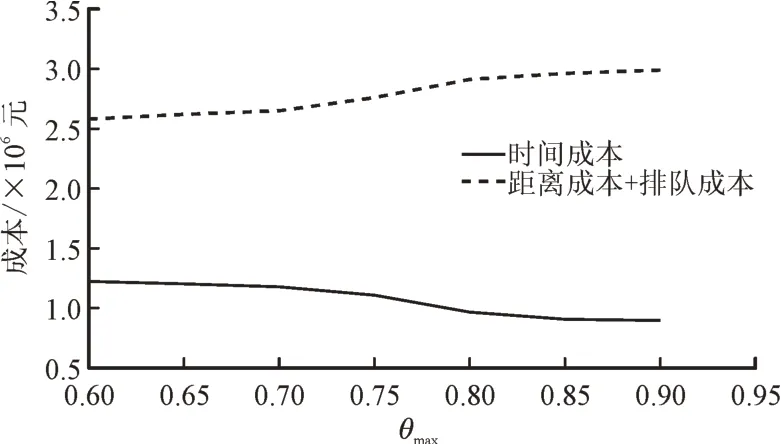
图4 θmax 对应为寻址时间权重时取值对各成本的影响Fig.4 Effect of θmax corresponding to the addressing time weight on each cost

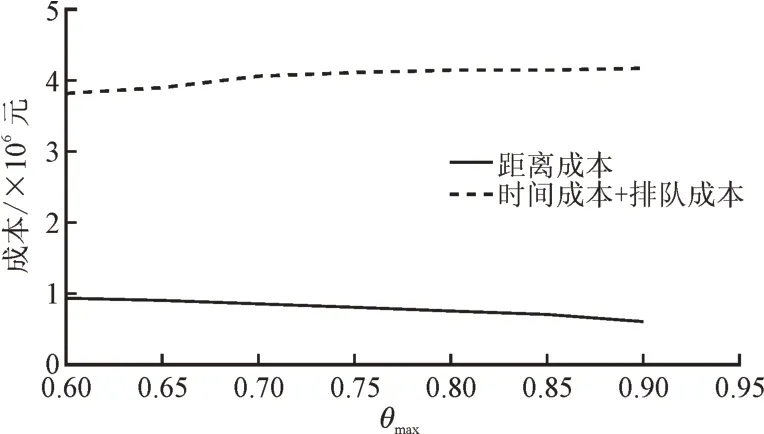
图5 θmax 对应为寻址距离权重时取值对各成本的影响Fig.5 Effect of θmax corresponding to the addressing distance weight on each cost

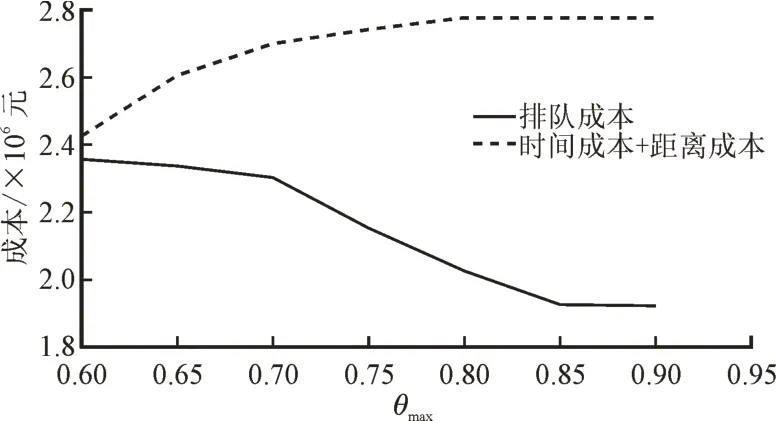
图6 θmax 对应为拥挤程度权重时取值对各成本的影响Fig.6 Effect of θmax corresponding to the degree of crowding weight on each cost

θmax分别对应3 个指标时的各成本变化趋势相似，故以图5 为例进行分析。从图5 可知，随着θmax的增大，分配给寻址距离的权重增加，用户最佳寻址合集中的候选电站偏向于寻址距离更近的充电站，相应的在选址定容步骤中每个用户对应的候选电站寻址距离更近，用户的距离成本更低；寻址时间和拥挤程度分配的权重减少，每个用户对应的候选电站的寻址时间更长，拥挤程度更大。这表明以距离用户最近的充电站为目标电站忽略了寻址时间、拥挤程度对布局优化结果的影响，且没有考虑每个用户的具体需求。因此，综合考虑用户对寻址时间、寻址距离、拥挤程度的选择偏好在充电设施布局优化求解中结果更可信。

3.2 充电设施布局优化结果及分析

为了对所提规划方法进行验证，在获得用户产生充电需求时的位置、需求偏好等多源数据基础上设置如下3 种规划方法进行对比分析。

方法1：同时考虑用户具体需求与社会总成本，即每个用户对应的候选电站在其各自的最佳选择合集中生成。

方法2：只考虑每个用户的具体需求，即每个用户对应的候选电站为其各自最佳选择合集中的。

方法3：只考虑社会总成本，对待用户单一考虑距离因素，即每个用户以其距离最近的候选电站为目标充电站。

根据图2所示的算法流程图计算得到3 种规划方法的最优选址定容结果如表3 所示。

表3 3种规划方法各成本对比Table 3 Cost comparison of three planning methods

方法1 为本文提出方法，其总成本为2 299 万，相比于方法2 和方法3 分别降低了5.74%，1.13%。进行选址定容步骤时，方法1 中每个用户对应的充电站可以随着算法的迭代在各自的最佳选择合集中选择更优解。但方法2 完全遵循用户的选择，每个用户对应的充电站固定为，这缩小了模型的优化空间，从而增大了基础建造成本与年运营成本，分别高出方法1 179.6 万元与39 万元，且占地面积5 268 m2，充电桩数量为439 个，远大于实际需求，造成了社会公共资源的浪费。

方法3 行驶距离成本最低，但没有考虑充电站拥挤程度，增大了用户排队成本；没有考虑道路实际交通拥堵情况导致行驶时间成本，分别比方法1和方法2 高出66.0%和62.3%。

相比于方法3，方法1 建造运营成本略高，但用户成本降低了7.30%。随着社会的发展，电动汽车的保有量将持续增加，产生的充电需求量将不断上升，用户成本也随之增大。从长远看，方法1 的优势将在未来体现得更为明显。

方法1 的布局优化方案中，各候选电站充电桩数量占总充电桩数量百分比与用户最佳选择合集中各候选充电站被选择次数占比如图7 所示。

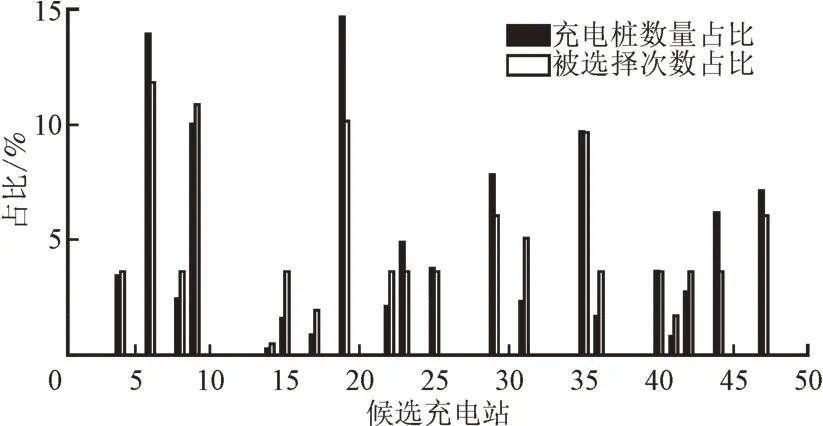
图7 布局优化方案和用户最佳选择合集对比Fig.7 Comparison of layout optimization scheme and user's best choice collection

由图7 可知，2 组数据基本吻合，这表明用户最佳选择合集可以在对充电站进行布局优化之前筛选出能够满足用户具体需求的候选电站。以用户最佳选择合集作为初始参数求解上层电动汽车充电站选址定容模型，可以在汽车充电站选址方案与定容研究时更为灵活，结果更优。

4 结论

本文基于多源数据，构建电动汽车充电站双层布局优化模型，旨在平衡电动汽车用户与充电站投资商利益的同时满足每个用户的具体需求，实例验证结论如下：

1）提出的双层布局优化模型明确考虑了电动汽车充电站布局过程中由于多源数据调整可能导致的布局方案的变化。通过设置充电用户的不同需求偏好，得到用户最佳选择合集并作为充电站选址定容优化模型的初始参数，相比于传统的以距离最近作为优化模型初始参数，可以准确描述用户需求偏好的变化对充电站布局的影响。

2）用户最佳选择模型可以对选址定容初始参数进行有效的预处理，结合选址定容模型能筛选出符合用户选择偏好的目标电站，并能降低充电站的用户成本与社会总成本，从长远看优化效果更明显。

3）在充电站布局优化过程中，如果单一考虑距离最短或完全遵循用户的选择，则会缩小模型的优化空间，增大社会总成本。这表明在电动汽车充电站布局规划中既要考虑多源数据对选址布局的影响，也要采用适当的方法进行布局优化。