基于数据驱动的新型电力系统潮流分析方法

龙 云，卢有飞，赵宏伟，包 涛，陈 晨，李更丰

（1.广东电网有限责任公司广州供电局，广东广州 510630；2.南方电网数字电网有限公司，广东广州 510000；3.西安交通大学电气工程学院，陕西西安 710049）

0 引言

电网状态感知能力是电网领域中的技术活动时必不可少的能力。结合数据分析处理与运行决策手段[1-2]，其能提高电网控制决策的效率和精准程度。目前，电网状态感知能力在军事、智能交通、计算机网络等领域得到了广泛的应用。国内电网企业以物联网技术的大范围部署为基础，以形成完整的电网状态感知预测调配系统[3-6]。

电力网络的数据采集是电网状态完成感知和调配的过程中必要的步骤。由于计算机技术与数字通的发展，数据采集技术已取得了重大进展[7-9]。随着大数据和物联网等技术的引入，数据采集技术逐步向智能化、高速化和网络化发展[10-11]。此外，电力系统正处于向新型电力系统发展的重要阶段。新型电力系统的主要特点是实现风光电的高比例接入[12-13]，其呈现的不确定性、控制复杂、弱惯性、数量大、分散化，使得对计算速度和质量的要求不断提高。而传统的潮流计算在新的发展环境中已出现了一些难以避免的问题。目前的传统潮流计算领域，诸如文献[14-15]关于传统潮流计算的研究大部分仍以改进牛顿法和P-Q 分解法为主。然而，这些方法在计算时间上面临着挑战，并且难以全面反映系统整体状态。

新型电力系统的电源侧不确定性和负荷侧灵活性使对电源和负荷直接建模的方法难以进行，并且传统的潮流计算对于源荷的不确定性需要分析大量计算场景，而基于数据驱动的方法则能有效提取电气量之间的特征关系，进行快速计算。目前，文献[16-20]已经设计了基于数据驱动的新型电力系统分析方法。文献[16]利用全连接深度神经网络（Deep Neural Network，DNN）构建了数据驱动的潮流分析模型，并进行快速潮流分析。文献[18]采用数据驱动模型进行线性化潮流分析，并结合了偏最小二乘法（Partial Least Squares，PLS）与贝叶斯线性回归（Bayesian Linear Regression，BLR）两种回归方法。文献[19]采用一个反向传播（Back Propagation，BP）神经网络进行线性潮流分析。文献[20]则采用改进的多输出支持向量机回归进行非线性潮流回归。

为满足未来新型电力系统对高精度实时潮流分析的需求，本文设计一种数据驱动的新型电力系统潮流分析方法，考虑新型电力系统的节点负荷和新能源出力波动作为特征输入，充分利用现有的海量数据，并应用数据驱动技术进行大数据挖掘。该分析方法通过数据驱动形式，大幅度降低对电网拓扑和模型参数的依赖；通过对设计的基于Dropout深度网络（Dropout Deep Neural Network，DDNN）进行参数训练，提高数据驱动模型的泛化能力；结合深度网络能快速预测潮流分析的电气量，解决传统潮流难以兼顾计算速度与精度的问题，并为电力系统规划与运行分析提供了快速且精确的潮流评估分析。此外，本文采用了某供电局110 kV 的20 节点的仿真系统验证了本文方法的有效性。

1 新型电力系统潮流分析特征构造

1.1 传统潮流分析

对于传统的潮流分析方法，主要采用牛顿-拉夫逊法进行潮流方程的求解。对于一个包含m个节点的电力系统，其潮流方程可以列写如下：

式中：PGi，QGi分别为节点i的发电机对应的有功功率和无功功率输出；PLi，QLi分别为接入节点i的有功负荷和无功负荷；Gij，Bij分别为连接节点i和节点j的i-j电导和电纳的负值；Ui，Uj分别为节点i和节点j的电压幅值；θij为节点i和节点j的电压角度差，即θij=θi-θj，其中θi和θj分别为节点i和节点j的电压角度。

1.2 适应源-网-荷变化的输入特征构造

基于新型电力系统的大量历史状态数据分析，需要收集影响各个节点潮流分析结果的变量数据，首先需要确定源-网-荷的潮流分析的输入输出特征。鉴于新型电力系统的主要特征是负荷和新能源出力实时变化[21]，负荷量和新能源出力对节点的潮流分析结果具有显著的影响，从而导致潮流产生波动。同时，负荷量和新能源出力也是在电网中不同类型节点变化方面较为统一且直观的指标，可以适应不同类型节点数据变化情况的衡量。故本文主要选取电力系统PQ 节点和平衡节点的负荷序列F={f1,f2,…,fn} 和新能源发电机的出力序列G={g1,g2,…,gN}，作为数据驱动预测模型的输入变量，其中n为PQ 节点和负荷节点的总数，N为新能源发电机的总数。

1.3 适应源-网-荷变化的输出特征构造

2 数据处理及数据驱动设计

2.1 面向潮流分析的数据驱动框架

对于基于数据驱动的潮流分析，其预测流程分为3 个步骤，如图1 所示：（1）确定PQ 节点的负荷历史序列，并根据该负荷序列，收集负荷输入对应的电压、功率潮流的输出数据，存储于数据池中，等待下一步操作；（2）根据收集数据，对网络的参数进行训练，训练前要去除线路功率为0 的潮流矩阵数据（代表实际线路不存在）；（3）根据实时的负荷序列，通过已训练完成的网络进行实时的潮流分析，实现对各节点的潮流输出进行快速预测。

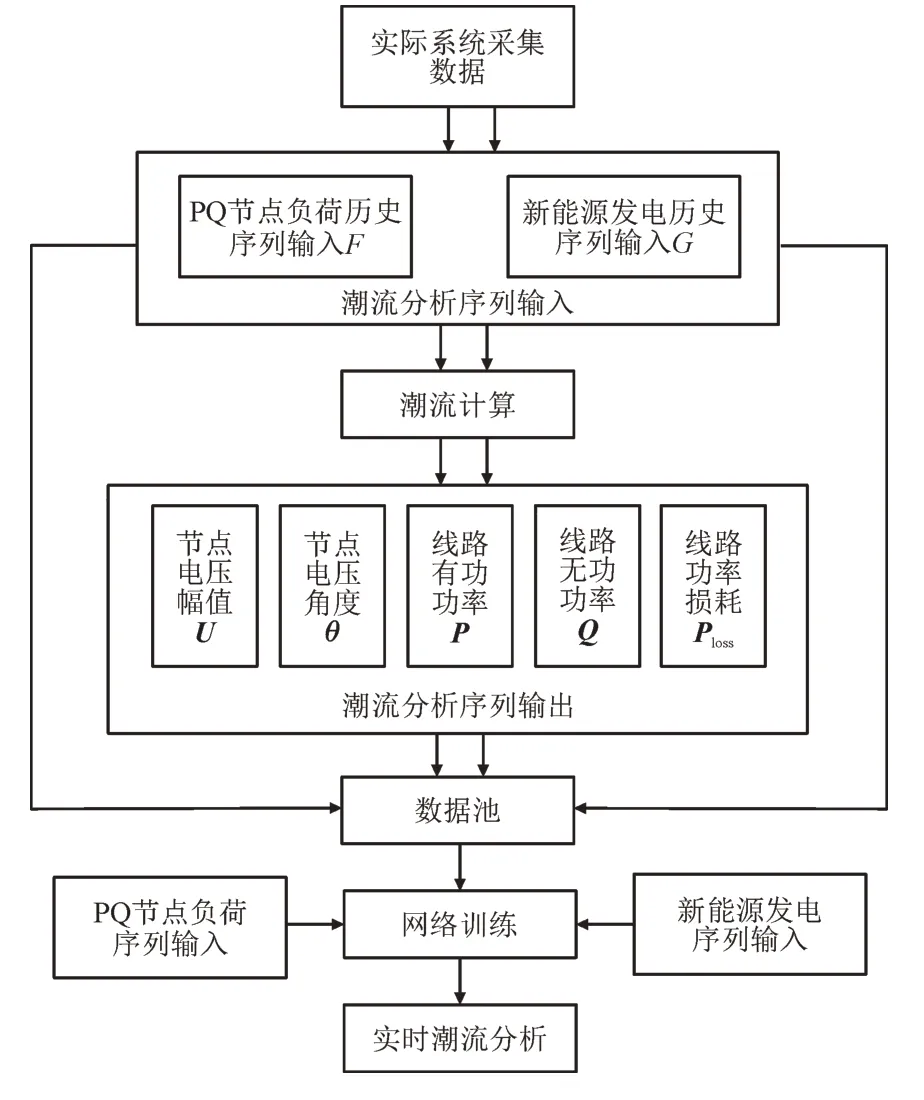
图1 预测流程图Fig.1 Flow diagram of prediction model

2.2 数据采集

由于实际电力系统的潮流分析中，获取的潮流矩阵为稀疏矩阵，很多节点之间并无直接连线。可以将功率潮流矩阵进行处理，去除等于0 或者接近于0 的维度，这样可减少训练参数。因此，本研究构建了一个包含（n+N）维负荷和新能源输入序列，以及（5e+2m）维潮流结果输出序列的模型，其中e代表电力系统节点拓扑中有效边数。

2.3 离线训练

网络的设计图如图2 所示。网络由输入层、隐藏层和输出层构成，其中每个隐含层应用了Relu 激活函数实现非线性化，并采用Dropout 操作[22]避免训练网络过拟合。

图2 网络设计图Fig.2 Flow diagram of network design

网络训练前，需要对数据进行归一化处理，数据处理过程可表示为：

2.4 基于数据驱动的潮流分析流程

本文提出的预测模型，包含全连接层和Relu 函数，其输出可表示为：

式中：hr为第r层网络的输出特征；wr为第r层网络的权重参数；br为第r层网络的偏置参数。

当模型参数训练完成后，网络便可以应用于对应系统的潮流分析。第一层输入特征h1为初始的输入负荷，最后一层输出hr为预测的潮流输出特征。传统潮流分析方法，需要求解潮流方程组，而本文提出的基于传统的潮流分析方法只需要最终训练完成的权重集合和偏置集合便可以计算结果输出，大大降低了计算成本。

3 仿真验证

3.1 参数设置

本文采用某供电局110 kV 电网数据作为仿真案例数据，系统拓扑图如图3 所示，电网系统的具体参数数据如表1 和表2 所示，其中电网的节点分类包括平衡节点、PQ 节点与PV 节点。本文利用获取到的某供电局基于系统历史运行的分钟级颗粒度状态数据对部分隐含层随机失活设计的全连接深度神经网络进行训练，训练数据的参数和网络的参数如表3 所示。其中，数据集1 为仅设定负荷数据变化案例；数据集2 为新能源与负荷动态变化案例，包括4 个月的长度数据，数据集的时间颗粒度为15 min。

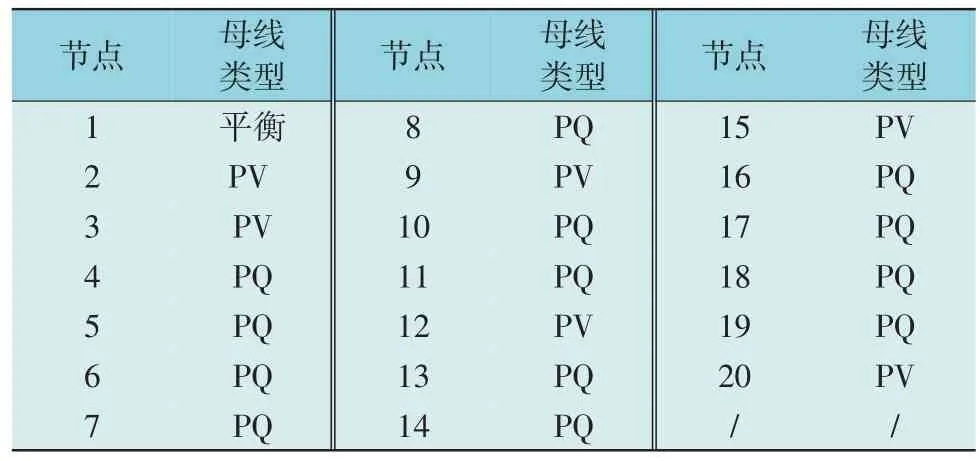
表1 系统节点类型Table 1 Bus type of system node

表2 系统线路参数Table 2 System line parameters

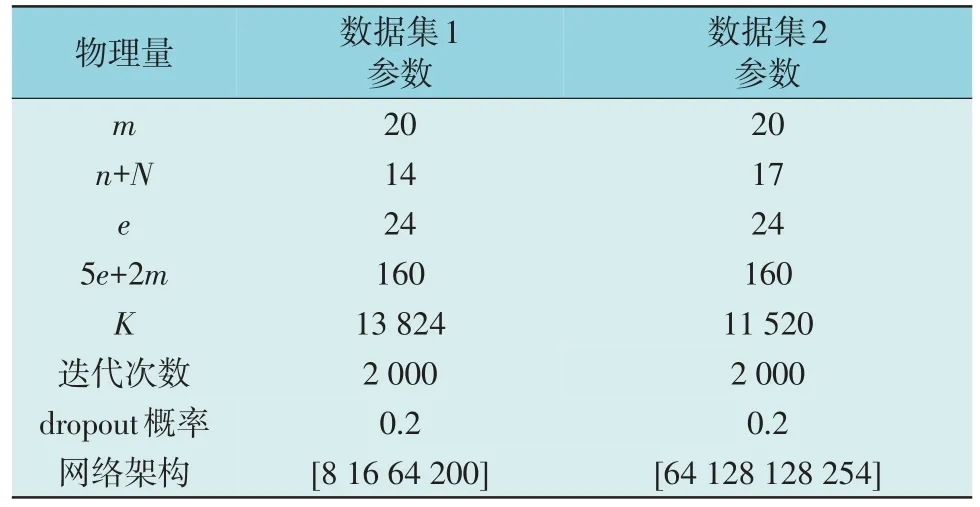
表3 模型参数设置Table 3 Parameters setting for model

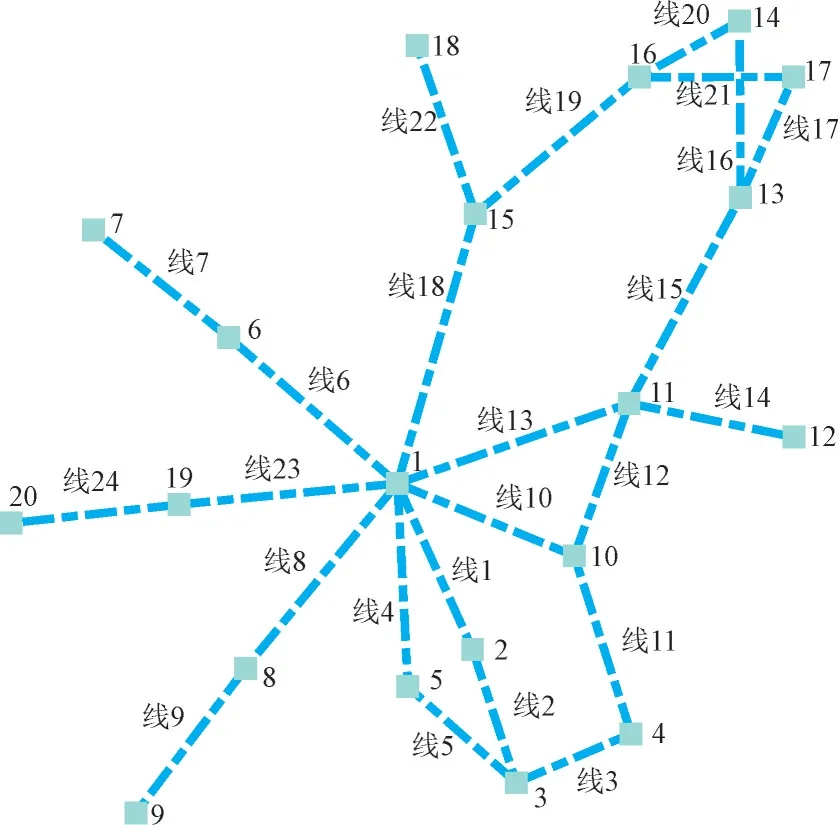
图3 系统拓扑图Fig.3 Power grid topology

3.2 离线训练

在该供电局的数据训练中，损失函数为平均绝对误差（Mean Absolute Error，MAE），预测模型的损失函数训练函数图如图4 所示。图4 中的实线代表训练过程中训练集的MAE 变化过程，虚线代表训练过程中验证集的MAE 变化过程，其为100 次迭代验证1 次。

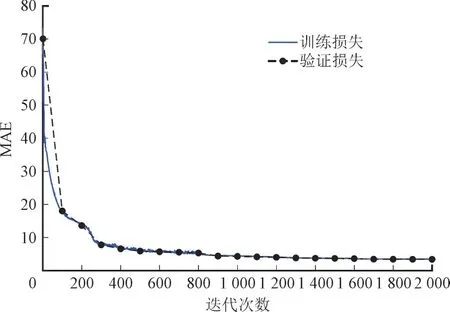
图4 训练损失函数图Fig.4 Loss function during training process

同时，对比基于DDNN 和传统潮流分析方法，图5 和图6 分别给出了某一负荷时刻下，20 个电力系统节点的电压分布对比和48 个线路功率潮流的对比。其中虚线表示传统潮流计算方法得到的数值，实线代表基于数据驱动的潮流分析方法获取的数值。

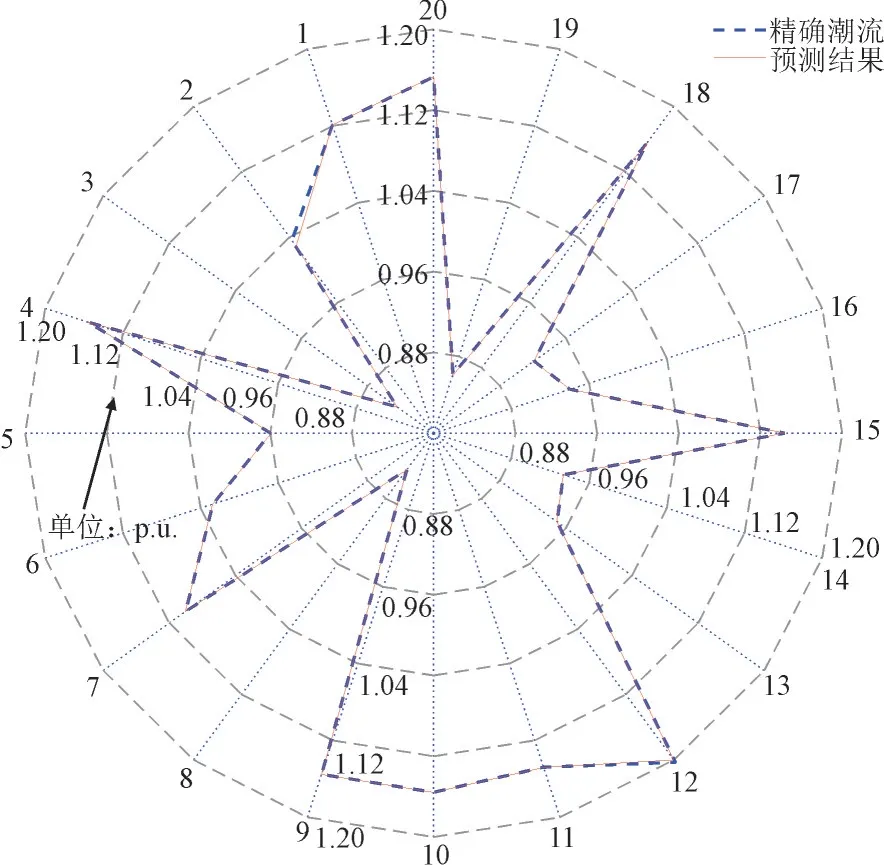
图5 电力系统20个节点电压分布预测对比结果图Fig.5 Comparison results for voltage distribution of 20 nodes in power system

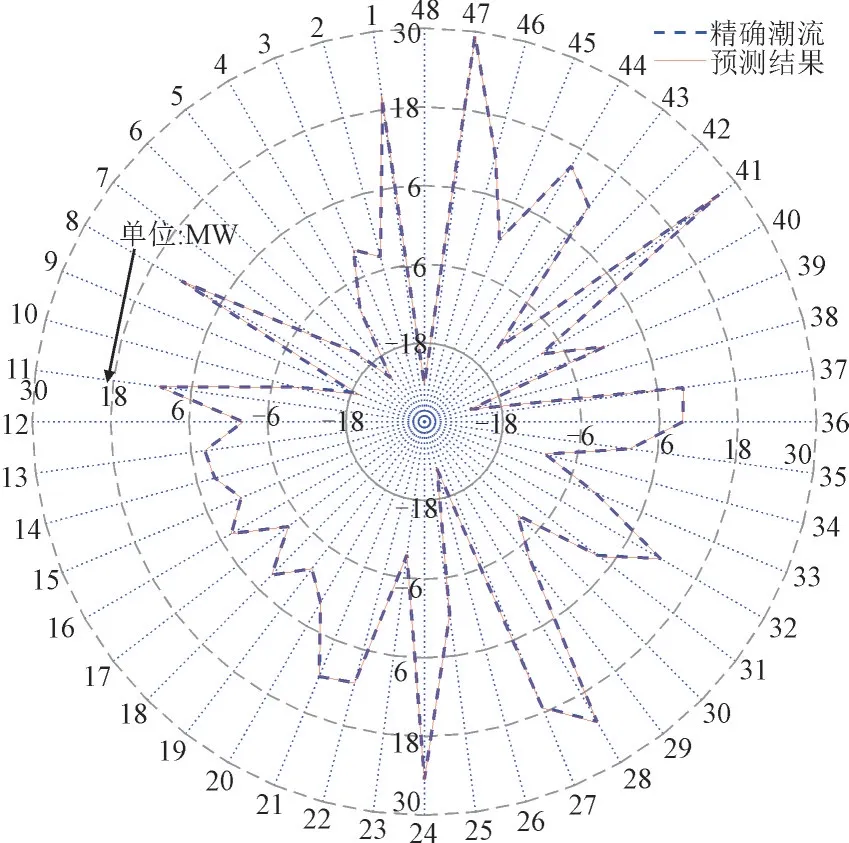
图6 电力系统24条传输线的潮流功率对比结果图Fig.6 Comparison results for power flow of 24 transmission lines in power system

从图5 和图6 可以看出，预测曲线和计算曲线的数值很接近，表明所提出基于数据驱动的方法获取的节点电压分布数据和功率潮流数据具有一定的精确度，可以替代传统方法进行潮流分析。通过仿真实验结果数据分析，可以得出潮流电压预测误差率仅有0.21%，而潮流功率预测误差率为0.93%。潮流计算时间与传统潮流计算相比，从原来的0.118 s 缩短至0.004 1 s。由此说明了本文所提方法具有在较短时间内进行相对准确的新型电力系统潮流计算预测的能力。基于数据驱动方法计算速度为毫秒级，可满足秒级颗粒度的实时潮流分析。

3.3 负荷动态变化案例

在负荷动态变化实验中，仍采用原来的电力系统进行潮流特征输出预测。通过调整其中2 个负荷节点（节点11 和节点14）的数值，对潮流的节点电压分布和传输线的潮流进行动态分析。节点1的电压分布如图7 所示，其中五角星的点代表在传统潮流计算分析下电力系统各个节点的潮流电压计算数值，圆形点代表本文数据驱动网络预测所得到的潮流电压计算预测数值。由图7 可知，随着负荷变化，由网络模型获取的节点电压分布与传统潮流分析计算的电压分布数值基本一致。

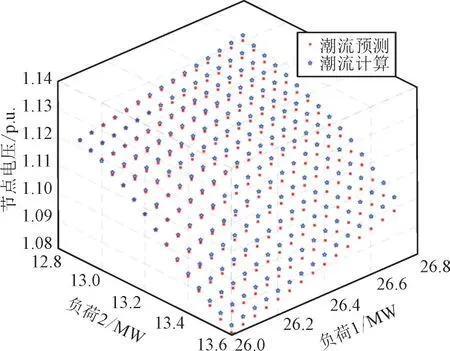
图7 节点1的电压幅值分布变化Fig.7 Voltage amplitude distribution change of node 1

此外，实验还选取了1 条传输线（线路1—8）的动态潮流数值进行分析。选取线路的动态潮流功率变化如图8 所示，为节点1 向节点8 发出的功率变化。随着负荷变化，由网络模型获取的传输潮流功率与传统潮流分析计算的潮流功率相比，两者变化趋势一致。总体的误差数值为0.41%，从线路功率角度，该方法可以替代传统的潮流分析方法进行节点电压预测。

图8 传输线1-8的潮流功率变化Fig.8 Power flow change for line 1-8

图9 对比了不同方法获取的电力系统的20 个节点电压幅值的平均百分比误差（Mean Percentage Error，MPE）。在所有节点中，与BLR 和PLS 相比，基于神经网络的方法（BP，DNN 与DDNN）能获取较小的电压相角。此外，图10 显示了不同方法获取的电力系统节点电压偏差情况。由图10 可以看出DDNN 能获取到电压幅值的偏差最小；从节点电压角度，该方法的节点电压角度预测误差小于6%，节点电压幅值小于0.5%。其中节点电压角度和幅值的预测平均误差分别为1.2%和0.058%，这说明其可以替代传统的潮流分析方法进行节点电压预测。

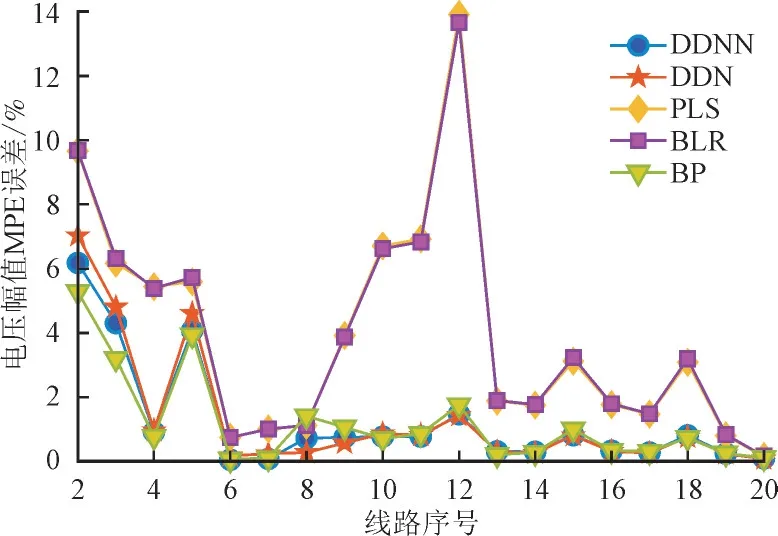
图9 电压相角MPE误差Fig.9 MPE of voltage phase angle

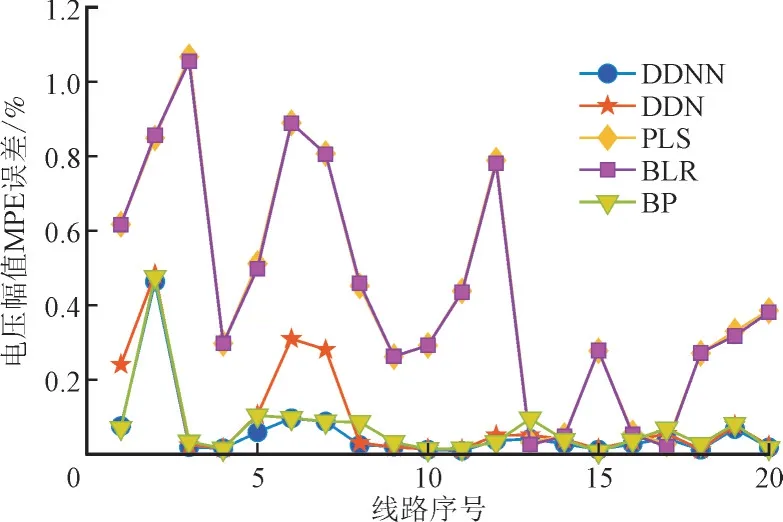
图10 电压幅值MPE误差Fig.10 MPE of voltage amplitude

此外，在负荷动态变化的对比实验中，还选取了DDN，PLS，BLS 和BP 4 种方法作为对比算法。表4 给出了不同线路的功率损耗预测误差，由表4可以看出DDNN，DNN 和BP 的误差均小于PLS 和BLR。这也说明了传统回归方法BLR 和PLS 不适用于基于海量数据的预测任务，而深度学习可有效提取电气量的特征。此外，除了线路4、线路12 和线路13 之外，DDNN 均能获得比DNN 较小的线路损耗预测数值，dropout 使DDNN 具有较好的预测精度和泛化能力。在多个线路的损失预测上，BP 网络的MPE 偏差与DDNN 接近甚至优于DDNN，但是其存在预测的不稳定性，如线路14 的MPE 为24.54%。

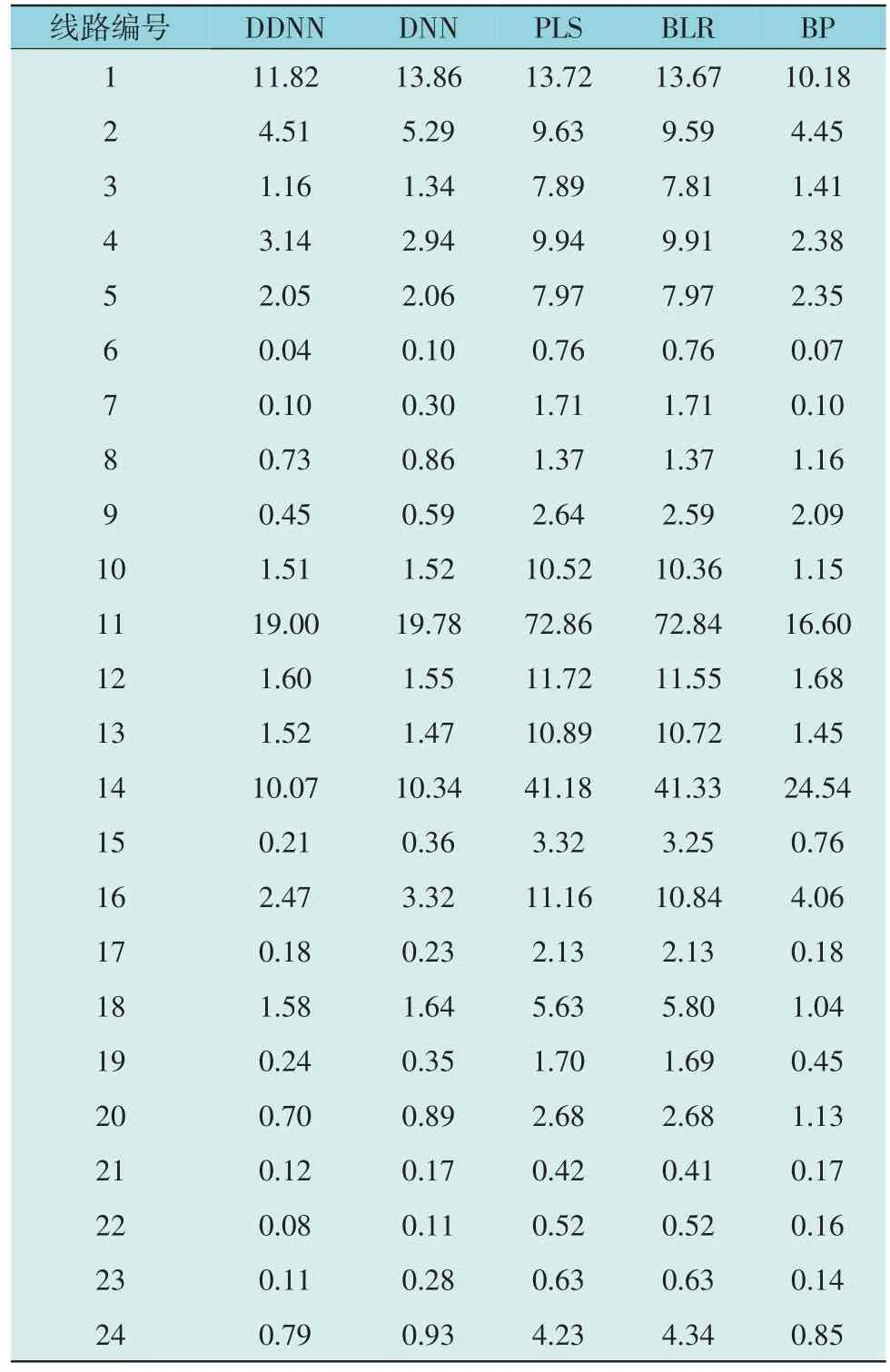
表4 线路损失预测MPE误差Table 4 MPE of line losses prediction %

3.4 新能源与负荷动态变化案例

为分析新能源机组的出力波动对新型电力系统的影响，本实验采用负荷与新能源出力同时变化的数据集2 进行网络参数训练。引入容量为15 MW的风电场和2 个容量为12 MW 和5 MW 的光伏电站。数据集2 新能源的部分波动数据如图11 所示。

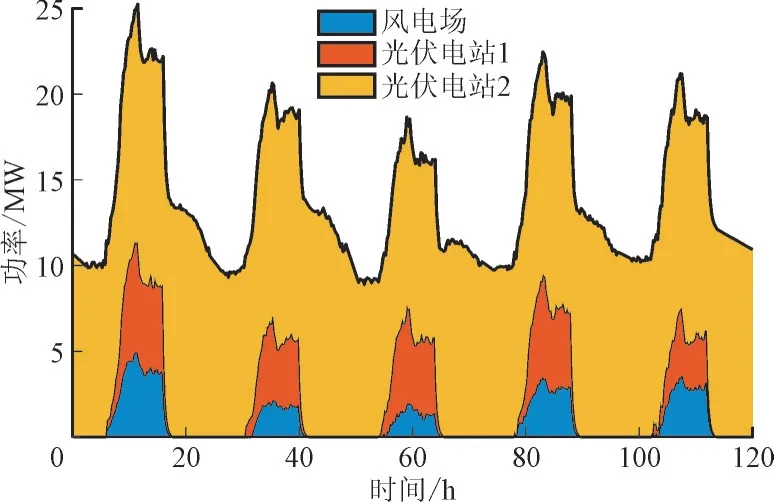
图11 新能源出力曲线Fig.11 New energy output curve

为验证DDNN 在时序场景的电气量特征提取能力，图12 和图13 了显示了在1 d 内，DDNN 与DNN 的电压幅值与传输线损耗的特征量数值对比。从图12 可以看出在位于负荷峰值9：00—16：00，DDNN 在节点9 的电压幅值预测与数据接近，而DNN 的预测值波动较大。从图13 中可以看出DDNN 的预测数据与数据值的偏差较小，尤其是12：00—16：00，DNN 难以反映该时刻线路的损耗变化。

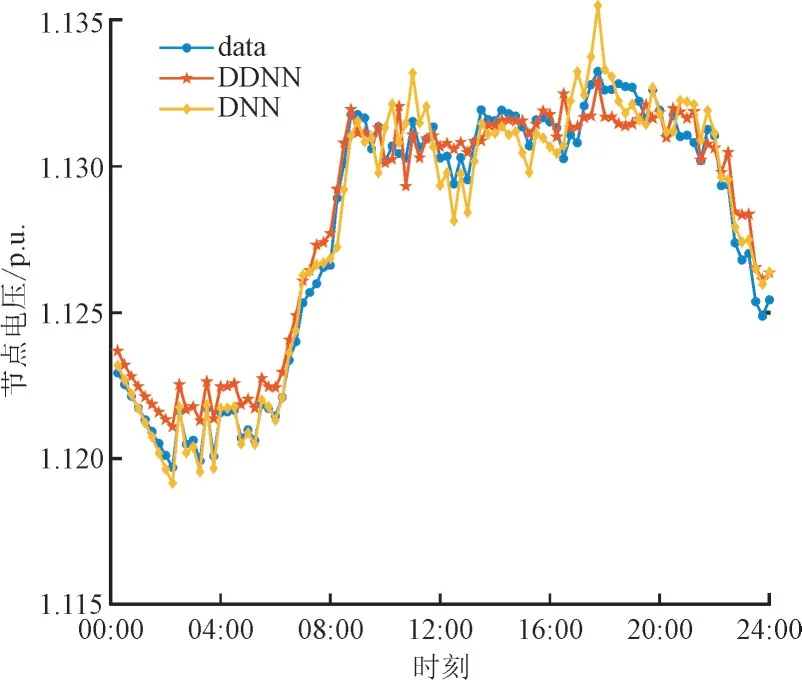
图12 节点9的电压幅值对比Fig.12 Comparison of voltage amplitude for node 9

为验证DDNN 对电力系统不同特征量的特征提取鲁棒性，本文利用数据集2 的验证集，计及新能源的出力波动预测存在15%的误差，对各个维度的线路功率参数在预测偏差进行计算。图14 展示了4 种算法在线路有功功率预测的偏差数据。从图4 中可以看出，在考虑新能源预测存在误差的情形下，PLS 和BLR 存在较大的线路有功功率预测偏差。其次是BP，大部分线路的有功功率偏差大于DDNN。之后是DNN，大部分线路的有功功率偏差大于DDNN。此外，如图15 所示，对于线路的无功功率预测，DDNN 的表现也优于其他3 种算法。值得注意的是，BP 在线路1 和9 的无功预测偏差在所有算法中最大，这也体现了其预测的稳定性较差。

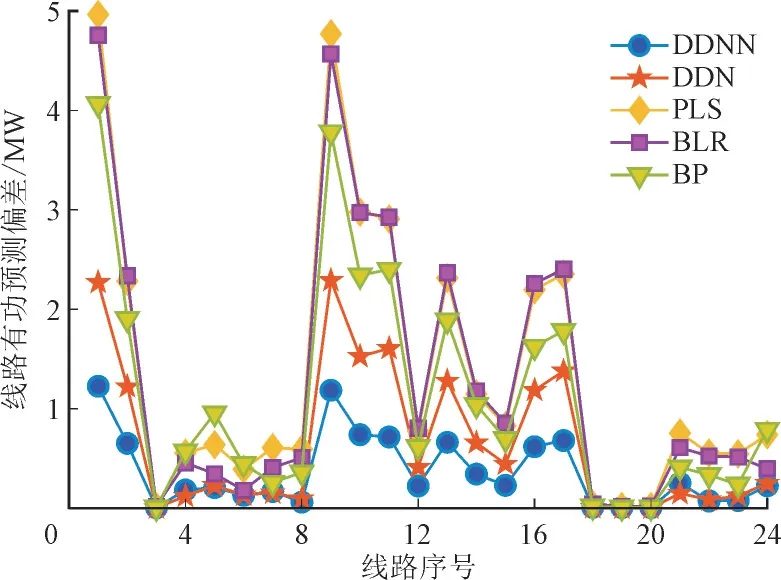
图14 线路有功预测偏差Fig.14 Active power prediction deviation of lines

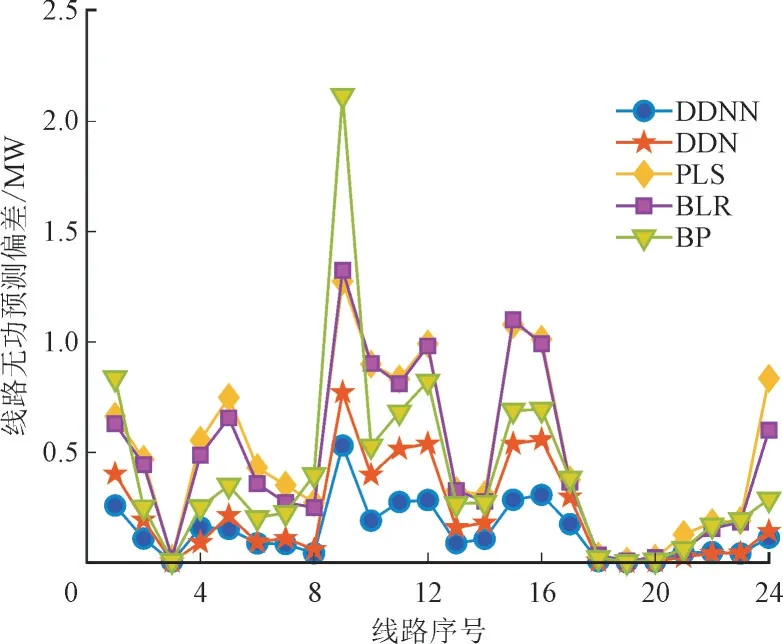
图15 线路无功预测偏差Fig.15 Reactive power prediction deviation of lines

4 结论

本文提出基于数据驱动的新型电力系统潮流分析方法，考虑了负荷和新能源的波动变化，应用数据驱动技术进行大数据挖掘，不依赖于电网复杂模型。此外，构建了一个部分隐含层随机失活的全连接深度神经网络，用于实时预测新型电力系统的潮流分析，该方法在能兼顾时间成本和预测精度。最后，在某供电局提供的系统历史运行的15 min 级颗粒度数据下进行网络训练，并与4 种回归方法进行对比，验证了该算法的性能。实验的节点电压和幅值预测结果与传统潮流计算相比，平均误差1.2%和0.058%。并且计算时间缩短近30 倍，可以满足毫秒级颗粒度的在线潮流分析。

本文方法根据输入特征数据来预测相应的潮流输出特征数据。然而，所采用的预测模型缺乏对历史时间序列知识的充分利用，并且在特征提取过程中对于电网拓扑信息也未进行有效利用。同时，部分线路的功率预测存在偏差过大情况，网络的泛化性能有待提高。在今后的研究中，将考虑时空图神经网络来对电力系统的时空信息进行挖掘，提升模型泛化能力，以实现更有效的潮流预测。