考虑设备安全的新能源场站参与电网频率协调控制方法

李登峰，张澳归，刘育明，欧阳金鑫，李小菊，姚 骏，杨旼才

（1.国网重庆电力科学研究院，重庆 401123；2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

近年来，由于全球矿物能源价格上涨，导致化石能源日益紧张，进而引起新能源需求急剧增长。随着新能源发电的战略地位日益提高，建设和投运规模也不断增长[1-2]。但高比例新能源并网也给现代电力系统带来了诸多挑战。风力发电和光伏发电是目前应用最为广泛的新能源发电，风电机组和光伏发电系统经变流器并网后会引起电网的惯性水平与调频能力大幅下降，导致电力系统频率稳定面临极大风险[3]。

频率安全是电力系统安全稳定运行的重要条件，现有电网导则通常要求风电机组和光伏发电系统等新能源需具备一定有功调节能力，确保及时响应电网频率的变化。虚拟同步机（Virtual Synchronous Generator，VSG）可模拟同步发电机的机电特性，使风电机组和光伏发电系统的有功功率跟随目标虚拟量的变化而变化[4]。VSG 控制类型主要包括：基于同步机运动方程的虚拟惯量控制[5]、基于多阶段切换的改进最大功率点跟踪（Maximum Power Point Tracking，MPPT）曲线控制[6]、基于直流电压的惯性支撑控制[7-8]。但现有VSG 的研究主要针对单台机组，难以实现机组之间的有效配合，其应用于大规模新能源场站的有效性还有待进一步验证。

新能源场站的容量巨大，具有较强的功率调节能力，在电力系统频率控制方面的作用显著[9]。文献[10]针对直流闭锁下送端电网的安全问题，提出新能源场站协同常规机组的紧急频率控制优化模型，在保证频率安全的同时使系统控制代价最小，缺点是忽略了设备安全对新能源场站控制能力的影响。文献[11]提出大规模集群可再生能源有功分层协调控制策略，通过逐层分类优化有功控制指令，实现系统运行安全性、经济性和控制公平性的协调优化。文献[12]以成本最小为目标，提出风储系统与同步机组的协调控制策略，可在满足系统调频需求的同时降低调频总成本及各风电场内载荷总量。文献[13]在降低风电机组运行成本的基础上，提出一种由风电场、风电机组、电池储能系统协调组成的有功功率输出分层惯性控制方法，其缺点在于储能电站建设成本较高、不能大规模投运且应用方面受到限制。

风电机组或光伏发电系统参与电网频率控制时，需频繁调整风电机组或光伏发电系统的出力，势必加速光伏电池板、风轮等设备的老化，使设备安全风险不断增加。风电机组疲劳载荷的连续变化可导致风机本体受损，从而影响机组的使用寿命[14-19]。光伏的功率调节则将加速光伏组件老化，导致光伏发电系统故障或失效。目前新能源参与电网运行控制主要以系统运行的经济性为目标，尚未考虑频率调控对设备安全性的影响。针对新能源场站间的协调控制，如何兼顾系统经济性与设备安全性，是当前亟需解决的问题。

为缓解新能源机组出力频繁调整对设备安全的影响，本文提出考虑设备安全的新能源场站参与电网频率协调控制方法。通过分析新能源参与电网频率控制对设备安全的影响，建立新能源场站参与电网频率控制的双层频率控制模型。算例分析表明，所提方法能有效抑制系统不平衡功率扰动下的频率波动，实现设备安全性和系统经济性最优。

1 电网双层频率控制模型框架

新能源场站参与电网频率控制时，电网双层频率控制模型框架如图1 所示。

图1 电网双层频率控制模型框架Fig.1 Grid double-layer frequency control framework

图1 中，ΔPd为系统不平衡有功功率变化量，ΔPsg,sh，ΔPwfs,sh，ΔPps,sh分别为同步机、风电场站和光伏场站的切机有功功率变化量，ΔPwfs,re，ΔPps,re分别为风电场站、光伏场站的有功功率调节变化量，为第j台风电机组的有功功率调节变化量，为第k台光伏机组的有功功率调节变化量。

由图1 可知，电网双层频率控制模型由上层频率控制模型和下层频率控制模型共同组成。电网调控中心检测到系统功率缺额时，利用上层频率控制模型，根据同步机和新能源场站的运行参数，决策同步机和新能源场站的有功功率调节量。进一步根据新能源场站中各机组的运行特征，利用下层频率控制模型确定各机组的有功功率调节量，从而实现新能源场站之间和站内的协调控制。

系统不平衡有功功率通常难以直接测量，可利用发电机端频率数据计算[18]。第q台发电机的不平衡有功功率变化量为：

式中：为第i台同步机的惯性时间常数；fnom为系统额定频率；f为系统频率；t为时间。

ΔPd的值等于所有同步机的不平衡有功功率变化量的总和，其表达式为：

通过对比系统有功功率备用总量和系统不平衡有功功率的大小以确定是否需要切机，具体分为2 种情况：（1）若备用总量大于需求量，仅依靠有功功率调节即可保证系统频率安全，则无需切机。基于下层频率控制模型求解风电场站和光伏场站调节量，依据设备安全指标分配场站内各机组的有功功率调节量。风电场站的安全指标选取疲劳载荷量，光伏场站的安全指标选取光伏组件老化成本；（2）若备用总量小于等于需求量，仅依靠功率调节难以保证系统频率安全，则需释放全部风光备用并切除机组。基于上层频率控制模型求解各场站的切机有功功率，按照最小欠切原则切除机组[20-22]，剩余场站仍按控制目标函数求解结果并进行有功功率调节[23-26]。

2 上层频率控制模型

2.1 新能源场站间协调模型目标函数

上层频率控制具体指同步机、风电场站、光伏场站等各新能源场站间的协调控制，其模型的控制成本包括新能源场站的切除成本和功率调节成本。在满足电网频率需求的前提下，新能源场站间的有功协调以控制成本最小为目标。新能源场站间协调模型的目标函数F1为：

2.2 约束条件

1）频率约束。为了避免频率越限，系统频率约束为：

式中：Δfsys为系统频率变化量；Δfsys,max为系统频率变化量最大值；Ksg,fr，Kwt,fr，Kpv,fr分别为同步机、风电机组和光伏机组的频率响应系数；ΔPsg,re为同步机有功功率调节变化量。

2）新能源场站功率调节量约束。根据电网导则要求[21]，新能源场站参与电力系统频率控制时，其功率调节量不小于10%运行功率，因此新能源场站的功率调节量约束为：

式中：Pwt,ac，Ppv,ac分别为风电机组、光伏机组的运行功率。

3）系统功率平衡约束。为保证新能源场站整体控制效果，各控制周期内场站间协调控制的功率调节量的总和须满足系统功率平衡约束为：

3 下层频率控制模型

下层频率控制模型由光伏场站和风电场站内部的协调控制模型组成。

3.1 光伏场站协调模型

光伏发电系统主要由太阳电池组件（方阵）、并网逆变器及其控制系统组成，太阳电池组件作为光伏发电系统的核心部件，长时间裸露运行加之外界环境影响可能导致光伏组件发生光学老化、电气老化或电势衰减老化等，降低光伏发电系统的使用寿命。另外，光伏出力调整也会引起光伏电池老化程度增加，进而导致机组寿命下降。因此，光伏电池老化成本可刻画光伏参与电网频率控制对设备安全的影响。光伏场站协调模型以光伏电池老化成本最小为目标，其目标函数F2为：

光伏场站协调模型的约束条件主要包括光伏有功出力约束和光伏场站功率约束。

1）光伏有功出力约束。各控制周期内各控制周期内各光伏有功功率不超过其功率调节的上下限值，满足光伏有功出力约束为：

2）光伏场站功率约束。控制周期内各光伏机组功率调节量的总和须等于光伏场站调节量，满足光伏功率约束为：

3.2 风电场站协调模型

风电机组主要由风轮机、发电机、背靠背变流器和控制系统组成。从疲劳载荷量角度刻画风电机组参与电网频率控制对设备安全的影响，以疲劳载荷量最小为目标确定风电场站每台风机的有功控制定值。风电场站协调模型的目标函数F3为：

根据风机动力学模型，疲劳载荷与风电机组出力的解析关系为[12]：

根据风机动力学模型及传动轴模型，得到风机角速度、桨距角、传动轴形变量与有功功率等系数的离散状态空间表达式为：

风电场站协调优化模型的约束条件主要包括风电机组有功出力约束与风电场功率求和约束。

1）风电场站有功出力约束。各控制周期内各控制周期内各风电场站有功功率不超过其功率调节的上下限值，满足风电场站有功出力约束为：

2）风电场功率求和约束。各控制周期内各风电机组的功率调节量的总和须满足风电场功率调节量求和约束为：

4 算例分析

现有研究多采用遗传算法求解模型，遗传算法可从多初点多路径寻找全局最优解，然而该算法容易出现“过早收敛”的问题，从而陷入局部最优。模拟退火算法基于模拟金属退火的原理，通过全局搜索找寻命题最优解，采用该方法可以克服上述问题但缺点是所需迭代次数较多。为了克服上述2 种算法各自的缺陷，将遗传算法和模拟退火算法相结合，在避免陷入局部最优的同时缩短模型计算时间。本文采用模拟退火—遗传融合算法求解双层频率控制模型，具体执行步骤如图2 所示。其中，ΔΓ为目标值的损失值，可通过新目标值和原作差求得，e-ΔΓ/Λ为Metropolis 准则中粒子在温度Λ时趋于平衡的概率，ϒrand为生成的随机数，由随机算法生成。

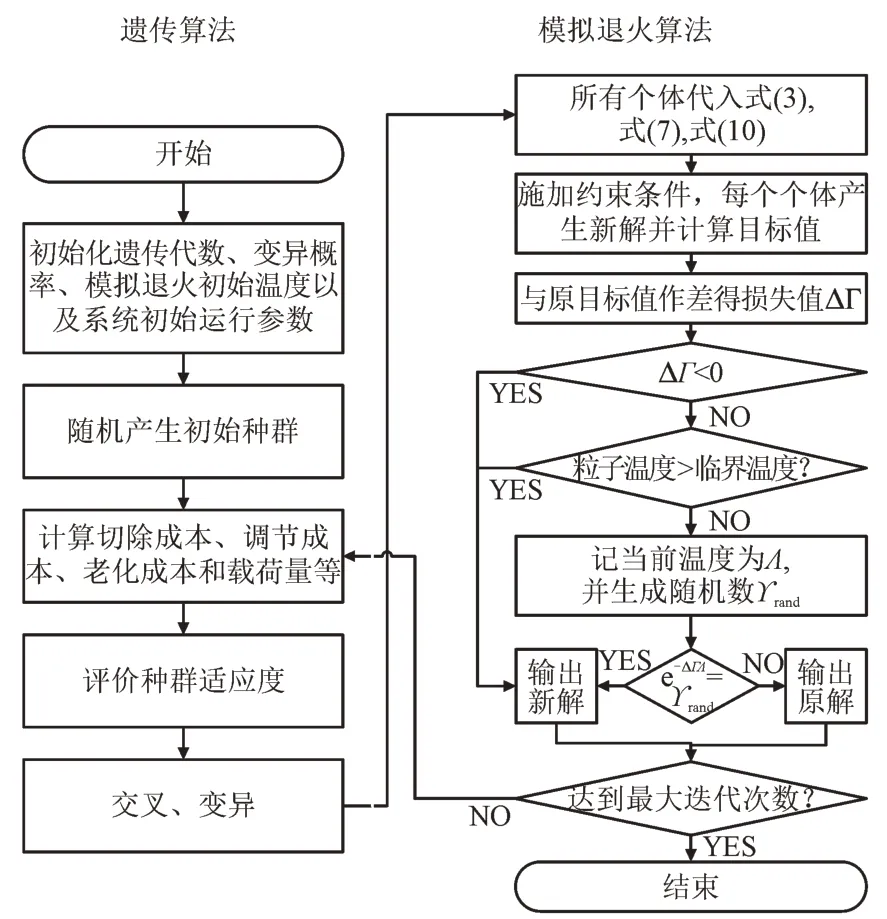
图2 模拟退火—遗传融合算法执行步骤Fig.2 Execution steps of simulated annealing-genetic fusion algorithm

由图2 可知，在Matlab 中利用模拟退火-遗传融合算法求解算例，并在Simulink 中验证控制方案的效果。首先，设置遗传代数、变异概率、模拟退火初始温度等数据；然后，计算种群适应度并生成变异种群，通过在前期（高温）减少个体间的适应度差异，后期（低温）放大个体间适应度差异，突出优秀个体并不断更新最佳适应度与全局最优解；最后，当达到最大迭代次数时，确定控制方案及优化目标值。

4.1 算例系统

本文研究采用IEEE 30 节点系统验证理论研究的正确性和有效性，算例系统如图3 所示。其中，WF1—WF3 为风电场站，PV5，PV8，PV13 为光伏场站，SG14，SG22，SG23，SG27 为同步机，节点1，2，3为风电场站接入节点，节点5，8，13 为光伏场站接入节点，节点14，22，23，27 为同步机接入节点。

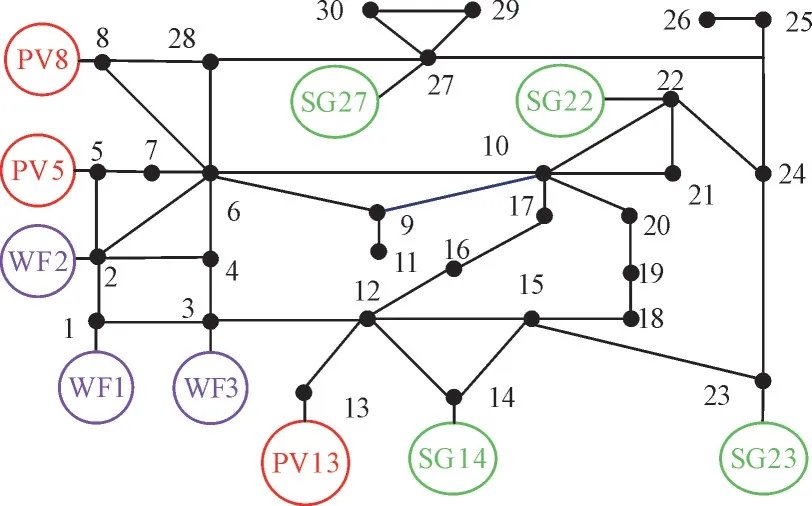
图3 算例系统Fig.3 Example System

结合新能源场站并网导则要求，新能源场站下调功率最大范围为额定功率的20%。新能源场站及同步机运行参数如表1—表2 所示。

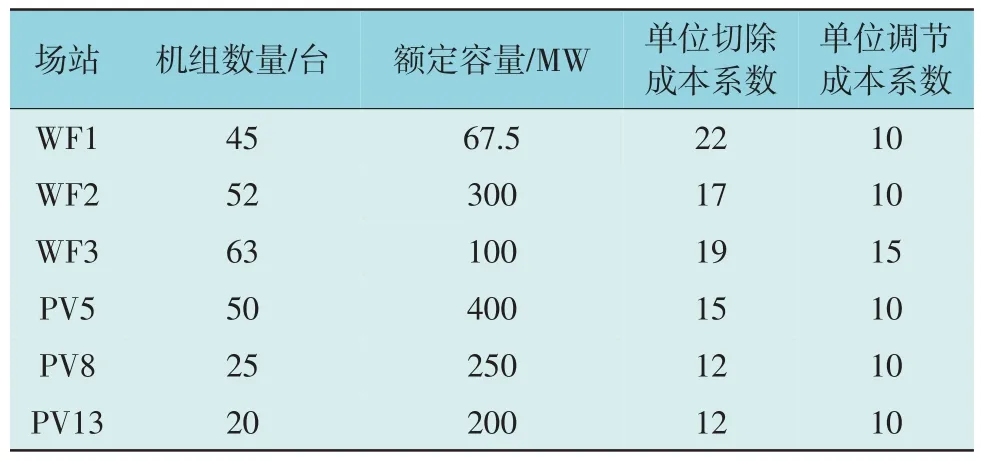
表1 新能源场站运行参数Table 1 Parameters of renewable energy station

表2 同步机运行参数Table 2 Parameters of synchronous generator

由表1—表2 可知，相较于同步机组，新能源场站具有更低的单位切除成本系数，说明优先切除新能源机组可以使控制方案的经济性更好。新能源场站的单位切除成本系数普遍高于单位调节成本系数，光伏场站的单位切除成本系数普遍低于风电场站。出于经济性的考虑，在系统频率不越限的前提下，优化算法将更倾向于功率调节或优先切除光伏场站。

初始化参数经调试后，设置遗传代数为100代、变异概率为0.1、模拟退火初始温度为500 ℃。方法1 为本文所提方法，方法2 为以最小欠切原则优先切除光伏场站，剩余不平衡功率量优先调控新能源场站。通过对比方法1 和方法2 的控制效果以验证本文所提控制方法的可行性。

4.2 300 MW功率盈余下控制效果

场景1 为支路10—22 因故障退出运行，由于潮流转移使系统出现300 MW 的功率盈余。利用模拟退火—遗传融合算法和粒子群算法求解方法1的时间分别为0.17 s，15.91 s。根据双层频率控制模型，可得300 MW 功率盈余下2 种方法的参数对比如表3 所示。

表3 300 MW功率盈余下2种方法控制参数对比Table 3 Control parameters comparison of two methods under 300 MW power surplus

由表3 可知，方法1 在故障发生后，WF1，WF2，PV5，PV8 分别减载10 MW，60 MW，80 MW，50 MW，减载功率均为其最大可下调功率，最大程度地释放了新能源场站的频率控制潜能。SG22 减载100 MW，与新能源场站配合，快速平抑了系统功率盈余。总控制成本为2 000 元。方法2 按运行功率由小到大切除光伏机组，在PV5 与PV8 中各切除了150 MW 的光伏功率。直至完全平抑系统功率盈余，方法2 的总控制成本为4 050 元。与方法2 相比，方法1 避免了切除机组，在降低控制成本的同时，也避免了因机组退出运行对系统造成的冲击。

场景1 下各新能源场站有功功率如图4 所示。

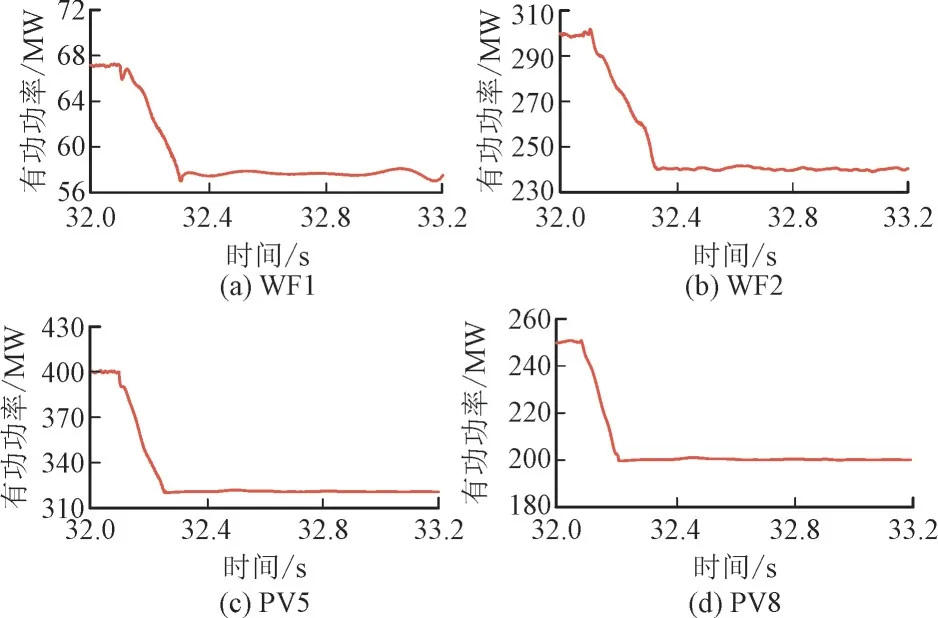
图4 场景1下各新能源场站有功功率Fig.4 Active power of renewable energy stations under case 1

由图4 可知，风电场站和光伏场站在故障发生后快速降功率，其中WF1 有功功率由67.5 MW 减载至57.5 MW；WF2 有功功率由300 MW 减载至240 MW；PV5 有功功率由400 MW 减载至320 MW；PV8 有功功率由250 MW 减载至200 MW。在有功功率达到指定控制值后，各场站均保持平稳的有功功率输出。

场景1 下系统频率如图5 所示。

图5 场景1下系统频率Fig.5 System frequency under case 1

由图5 可知，支路10—22 在第32 s 发生故障后，引发系统功率不平衡，导致频率快速上升并不断波动。采用方法1 时，在故障发生后较短的时间内系统频率即得到有效控制，暂态最大频率为50.291 Hz，稳态频率趋近于额定频率值，表明方法1可确保系统频率安全。采用方法2 时，系统最大暂态频率为54.967 Hz，远大于方法1，且方法2 作用下的频率波动较方法1 更严重，不利于系统的频率安全，表明方法2 难以保障在第一时间平抑功率扰动。

4.3 500 MW功率盈余下控制效果

场景2 为支路25—26 发生故障，伴随故障切除产生系统功率盈余500 MW。利用模拟退火—遗传融合算法和粒子群算法求解方法1 的时间分别为0.12 s，17.21 s。与单一算法相比，模拟退火—遗传融合算法在处理组合优化问题时具有较高的鲁棒性与更快的处理速度。根据双层频率控制模型，可得500 MW 功率盈余下2 种方法的参数对比如表4 所示。

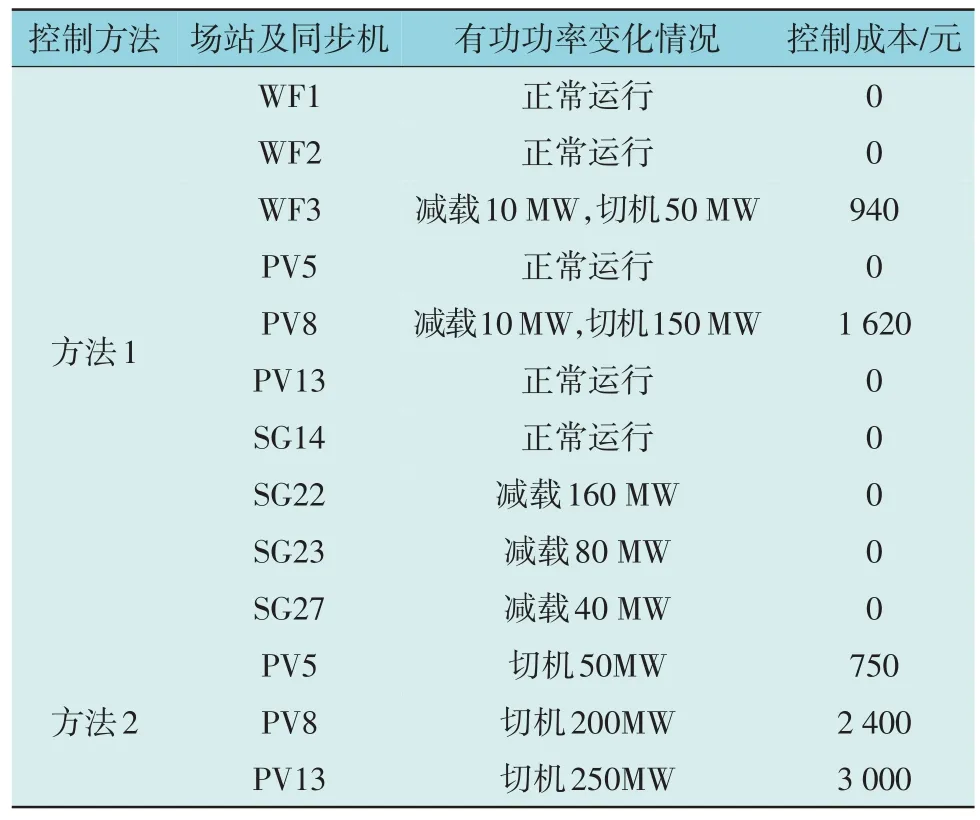
表4 500 MW功率盈余下2种方法控制参数对比Table 4 Control parameters comparison of two methods under 500 MW power surplus

由表4 可知，方法1 在故障发生后，SG22，SG23，SG27 分别减少有功功率输出160 MW，80 MW，40 MW。WF3 减少有功功率输出10 MW，PV8 减少有功功率输出10 MW，并切除WF3 与PV8 剩余共200 MW 的机组。切机后，剩余机组均保持正常运行以防止过度频繁的调频动作而导致的机组老化和磨损，其总控制成本为2 560 元。方法2 则按运行功率由小到大切除光伏机组，分别切除了PV8，PV13，PV5 中运行功率为200 MW，250 MW，50 MW的机组以平抑功率盈余，方法2 的总控制成本为6 150 元。与方法2 相比，方法1 通过调节部分新能源机组功率代替切机，有效地降低了控制成本。

场景2 下各新能源场站有功功率如图6 所示。

图6 场景2下各新能源场站有功功率Fig.6 Active power of renewable energy stations under case 2

由图6 可知，由于切除机组使得WF3，PV8 的有功功率在第32 s 出现跳变，导致剩余机组进行功率调节。WF3 的有功功率输出变为40 MW，PV8 的有功功率输出变为90 MW。

场景2 下系统频率如图7 所示。

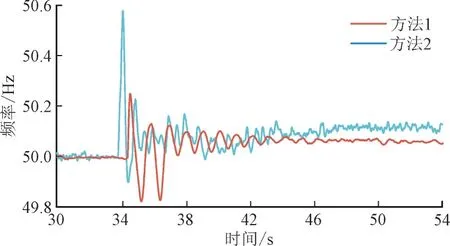
图7 场景2下系统频率Fig.7 System frequency under case 2

由图7 可知，在方法1 的作用下，系统频率最大偏差可控制在±0.2 Hz 左右，稳态频率为50.03 Hz，能够有效避免频率越限。在方法2 下作用下，系统最大暂态频率为50.58 Hz，出现了频率越限，且在达到最大暂态频率后频率出现大幅振荡，严重威胁系统频率安全。与方法2 相比，方法1 在兼顾经济性的同时，更为有效地实现了电力系统频率的控制。

5 结语

随着高比例新能源电力系统的频率稳定问题日益凸出，新能源场站更为频繁地参与到电力系统频率控制中。为缓解新能源机组出力频繁调整对设备安全的影响，提出考虑设备安全的新能源场站参与电网频率协调控制方法。所提双层频率控制模型实现了新能源场站间和场站内的有功功率协调控制，在兼顾系统经济性和设备安全性的同时，充分利用了新能源场站的功率控制能力，提高了新能源电力系统的频率支撑能力。