基于Bi-S-SRU的电力系统暂态稳定预防控制

刘颂凯，杨明飞，苏 攀，肖 兵，刘 旭，谭 瑞，周 倩

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.新能源微电网湖北省协同创新中心，湖北宜昌 443002；3.宜都兴发化工有限公司，湖北宜昌 443002；4.国网浙江省电力有限公司超高压分公司，浙江杭州 311121）

0 引言

随着经济快速发展和人民生活质量显著提高，人民生产、生活对电能产量和质量的需求也与日俱增，我国电力系统的规模和复杂程度也逐渐加深，系统运行状况变得更加多变且迫近其稳定极限[1-3]。一旦发生严重的突发事件，系统的稳定性可能会被破坏，连锁失效可能会导致巨大的经济损失和灾难性后果[4-6]。

电力系统暂态稳定预防控制是在故障发生之前启动的，通过调整系统的运行点，使其能够承受住可能发生的突发事件，保持稳定运行。预防控制实质上是一个考虑暂态稳定约束的最优潮流（Transient Stability Constrained Optimal Power Flow，TSCOPF）问题[7]，文献[8]通过将微分方程转化为差分方程，将半无限TSCOPF 问题转化为常规的非线性优化问题，但有可能发生维数灾难。为解决该问题，文献[9-10]将包含多台发电机的复杂电力系统简化为一个单机无穷大等效系统。文献[11]将扩展等面积准则引入TSCOPF 模型。文献[8-11]中所述方法均可处理电力系统暂态稳定问题，但所得结果精度有限，误差较大，且计算耗时较长，不符合在线快速应用的需求。

数据驱动算法可快速发现输入与输出之间的潜在规律，在电力系统暂态稳定预防控制领域发挥了重要作用[12]。文献[13]提出基于深度置信网络的电网暂态稳定评估器，嵌入到NSGA-II 进化算法的迭代寻优过程中，求取发电再调度预防控制策略。文献[14-15]分别使用两阶段支持向量机和两阶段贝叶斯网络进行暂态稳定评估和预防控制。尽管数据驱动算法在电力系统暂态稳定预防控制领域有了一定的发展，但常见的数据驱动算法大部分对时间序列数据的感知能力不强，难以挖掘电力系统运行数据中蕴含的动态信息。

因此，本文提出一种基于双向堆叠简单循环单元（Bi-directional Stacked Simple Recurrent Unit，Bi-S-SRU）的电力系统暂态稳定预防控制方法。通过引入Bi-S-SRU 模型进行暂态稳定预测，建立输入特征与暂态稳定指标之间的映射关系，用该映射关系替代传统TSCOPF 模型中的非线性微分代数方程，以简化计算与稳定验证过程；此外，考虑到传统的数学方法很难解决由数据驱动算法导出的具有隐式“黑盒约束”的优化问题，采用自适应粒子群优化算法（Adaptive Particle Swarm Optimization，APSO），考虑系统稳定性和发电调度成本最小化，形成预防控制策略。在IEEE 39 节点系统上的测试验证了所提方法具有可行性。

1 Bi-S-SRU评估模型原理

1.1 简单循环单元

简单循环单元（Simple Recurrent Unit，SRU）是一种基于循环神经网络[16-17]（Recurrent Neural Network，RNN）的改进神经网络，其在RNN 的隐藏层中添加了“细胞”部分，用于判别和过滤训练过程中的有效信息[18]。

SRU 通过“门控”结构决定不同时刻通过“细胞”的信息量，并解除了当前时刻t的输出St对前一时刻t-1 的输出St-1的强依赖性，在不损失精度的情况下提高整体计算效率。此外，通过门控设计，可以缓解RNN 中的更新梯度消失和梯度爆炸问题[19]，减少训练过程中预测值与真实值的偏差。

SRU 在当前时刻t下的计算原理如下：

式中：ft为t时刻的遗忘门；rt为t时刻的重置门；为t时刻的备选隐含状态；ht为t时刻的最终隐含状态；ht-1为t-1 时刻的隐含状态；xt为t时刻的输入变量；Wf，Wr，W分别为ft，rt，xt的参数矩阵；vf，vr分别为ft，rt的权重；bf，br分别为ft，rt的偏置向量；⊙为跳跃连接；σ为激活函数sigmoid；g为tanh 函数。

1.2 双向堆叠简单循环单元

SRU 在处理时间序列数据时，信息传递只是单向的，导致忽略了未来时刻的数据信息。为了解决该问题，文中提出Bi-S-SRU 改进模型。其基本思想是在每个训练序列中叠加1 个前向SRU 和1 个后向SRU，2 个SRU 连接到同一个输出层。该结构为输出层的输入序列中的每个点提供过去和未来的数据信息，使得数据信息存取更加充分。Bi-SSRU 网络结构如图1 所示。其中，W1和W3为输入层到前向和后向隐藏层的权值矩阵，W2和W5为隐层间传递的权值矩阵，W4和W6为前向和后向隐藏层到输出的权值矩阵，h为隐含状态，xt-1为t-1时刻的输入变量。另外，前向和后向隐藏层之间没有信息流，保证了非循环性。

图1 Bi-S-SRU结构Fig.1 Structure of Bi-S-SRU

2 含Bi-S-SRU 约束的预防控制决策模型

传统的TSCOPF 的暂态稳定约束往往依赖于微分代数方程[20]，存在计算量过大的问题。本文引入基于Bi-S-SRU 的暂态稳定预测模块来替代TSCOPF 模型中计算最复杂的部分，其计算效率远高于时域仿真，并以发电机有功出力调整为主要手段，利用APSO 优化算法实现预防控制的快速求解。

2.1 目标函数

以发电机有功出力调整总成本Fcost最小为目标函数：

式中：CUi为第i台发电机有功出力的上调单位成本；CDi为其有功出力的下调单位成本；ΔPUi和ΔPDi分别为第i台发电机有功出力上调量和下调量；SG为可调发电机的集合。

2.2 等式约束

潮流方程为：

式中：PNk为节点k的有功输入功率；PMk为节点k的有功输出功率；QNk，QMk分别为节点k的无功输入和输出功率；Vk，Vj为分别为节点k与节点j的电压幅值；αkj为节点k与节点j之间的电压相角差；Gkj，Bkj分别为节点k与节点j之间导纳的实部和虚部；Sn为所有节点集合。

2.3 不等式约束

电力系统正常运行需满足的稳定不等式约束如式（7）所示：

2.4 暂态稳定约束

暂态稳定约束的目的在于判断采取预防控制措施后系统的稳定性。文中利用Bi-S-SRU 在大量样本中挖掘系统运行数据与暂态稳定之间蕴含的规则，将微分代数方程表示的传统暂态稳定约束转化为基于Bi-S-SRU 的快速预测为：

式中：u为预防控制后的运行特征；ε为电力系统暂态稳定裕度；Ψ(·)为基于Bi-S-SRU 的隐函数，其输入为调整后的可控变量，输出为该出力场景下的暂态稳定系数预测值。

当预测发生最严重故障后系统仍能够满足一定稳定裕度时，认为系统是暂态稳定的。本文设置ε=10，即当暂态稳定系数大于等于10 时认为系统是暂态稳定的，反之为不稳定。

2.5 预防控制优化算法

内点法[21]、牛顿法[22]等传统的优化算法过于依赖模型的建立，对非线性优化问题难以求解，且无法解决带有隐式“黑盒约束”公式的优化问题。因此，越来越多的智能优化算法被应用于求解最优化问题。

粒子群算法（Particle Swarm Optimization，PSO）源于鸟群捕食的生物学活动，其基本思想是种群个体之间相互分享彼此的信息，通过合作找寻最优解[23-24]。PSO 具有易实现、参数少、收敛速度快等优势，已广泛应用于求解优化问题。但是传统的PSO 线性减小惯性权重，可能导致局部最优，因此文中采用APSO 算法求解TSCOPF 问题，使用自适应惯性权重和速度系数，使它们随着迭代过程自动调整，提高全局搜索能力和收敛速度。

3 电力系统暂态稳定预防控制流程

当电力系统在某一运行点上被预测为不稳定时，本文采用发电机有功出力调整措施，将系统从不稳定的运行点恢复到稳定的运行点，实现在线预防控制。所提出的在线预防控制方法的流程图如图2 所示。

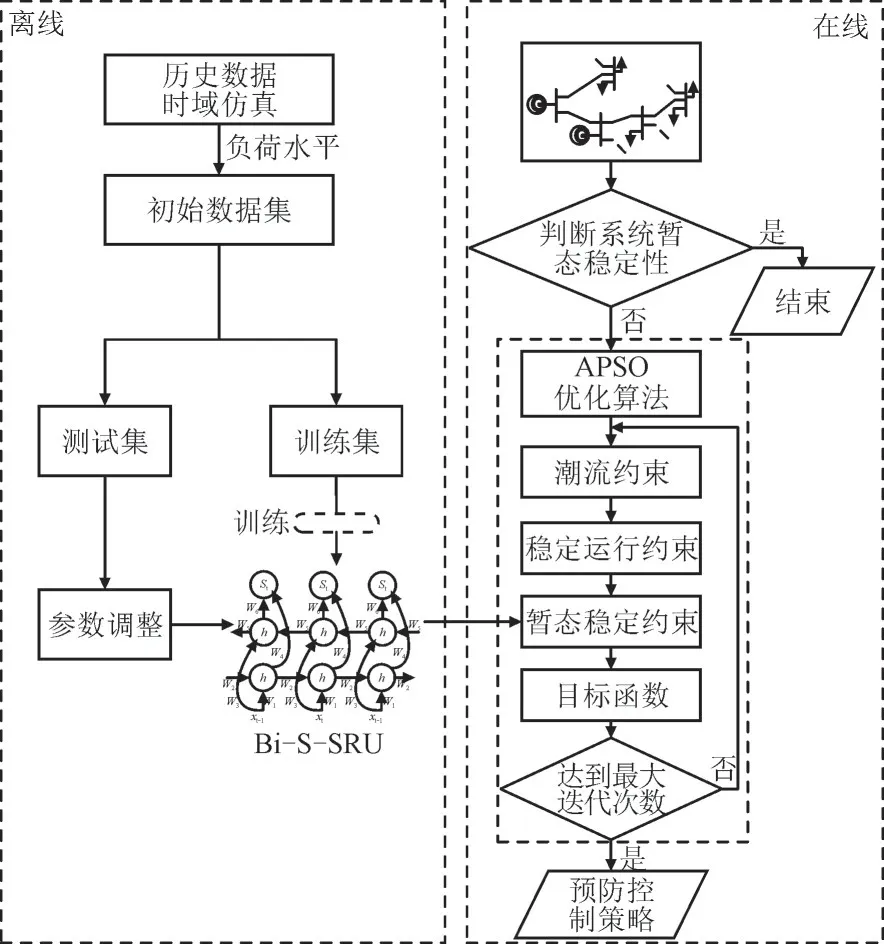
图2 暂态稳定预防控制流程图Fig.2 Flowchart of transient stability preventive control

3.1 样本生成

为了获得良好的训练性能，需要大量电力系统的运行数据，本文采用系统在不同负荷水平下的历史发电调度数据和电力系统仿真软件生成的发电机有功功率、电压幅值、负载有功功率、无功功率构建输入特征，生成一个初始数据集。针对预想故障集中的故障，对初始数据集中的每个样本进行时域仿真计算，记录其暂态稳定性。

选取暂态稳定系数作为每个样本的暂态稳定指标ITS，并作为每个样本的标签：

式中：δmax为任意2 台发电机之间最大功角差。

通常情况下，当ITS>0 时，系统处于暂态稳定状态；当ITS<0 时，系统处于暂态失稳状态。ITS越大，系统暂态稳定性越高。当采用ITS=0 作为暂态稳定裕度时，电力系统中不可避免地会存在临界稳定与临界失稳情况[25-29]，因此，为了保证电网的安全稳定运行，加强对失稳样本的识别能力，本文将暂态稳定裕度ε设置为10。

3.2 Bi-S-SRU模型训练

基于生成的初始数据集，对Bi-S-SRU 模型进行训练，使模型可充分学习到电力系统运行特性与暂态稳定系数指标之间的映射关系，并预测出对应预想故障与运行场景下的暂态稳定系数，保证预测的准确率，挖掘并形成系统运行特征与暂态稳定性之间的映射关系。将经过训练后的Bi-S-SRU 模型作为暂态稳定约束嵌入到TSCOPF 中，降低计算复杂度，使得后续制定预防控制策略时，能够快速判断系统的暂态稳定性。

3.3 预防控制优化

在TSCOPF 模型基础上，当系统所处运行点根据ITS与ε的关系被判定为不稳定时，通过APSO 算法进行优化计算，获得系统最佳运行点；系统运行人员由此采取相应的预防控制措施，使系统在稳定运行的同时，实现有功出力调整总成本最小的目标。

3.4 模型性能评价指标

为了验证所采用Bi-S-SRU 模型的性能优越性，采用预测准确率Ap评价模型的性能：

式中：Ir为样本的实际ITS值；Ip为模型预测的ITS值。

由式（10）可知，当预测值与真实值越相近，此时的预测准确率越高，即模型的性能越优越。

4 算例分析

在IEEE 39 节点测试系统上对本文所提暂态稳定预防控制方法进行算例分析，测试环境为Intel（R）Core（TM）i7-7700 CPU，8.0 GB RAM。

4.1 数据集生成

IEEE 39 节点系统由10 台发电机、12 台变压器和34 条支路构成。根据历史运行经验，考虑到故障的严重性，选择6 条线路构成预想故障集，如表1所示。

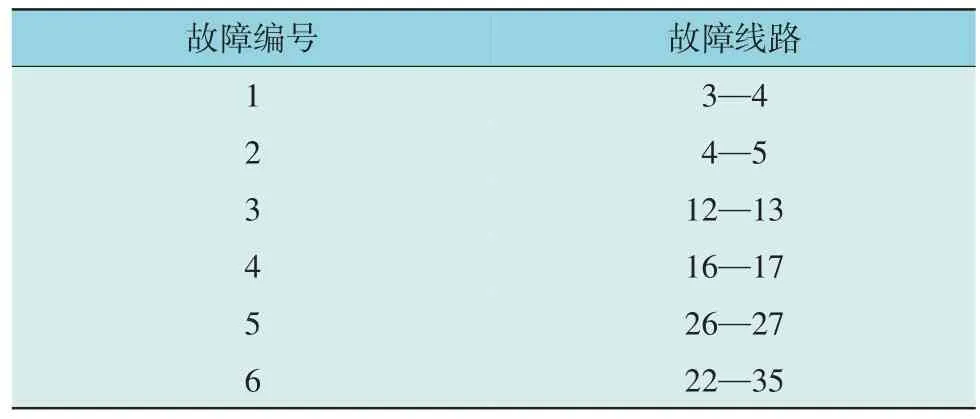
表1 IEEE 39节点测试系统的预想故障集Table 1 Expected fault set of IEEE 39-bus test system

设置三相短路故障，故障位置分别设在线路两端，故障清除时间0.1 s；假定发电机输出和负载的有功功率在其原始值的80%～120%之间波动，发电机的电压幅值在1.0～1.05 p.u.范围内波动；负载的无功功率由有功功率得出，以确保恒定的功率因数。在考虑发生预想故障前提下，最终生成5 700个样本，得到初始数据集，每个样本由发电机有功功率、电压幅值以及负载有功功率、无功功率和暂态稳定系数组成。

4.2 暂态稳定评估模型性能对比

采用五折交叉验证法，随机选取初始数据集中的80%样本作为训练集，剩余20%样本作为测试集，对Bi-S-SRU 模型进行测试。

为了体现Bi-S-SRU 模型的优势，本文将其与RNN、长短期记忆网络（Long Short-Term Memory，LSTM）、SRU 模型进行暂态稳定预测对比测试。输入样本维度设置为4，输出层维度均为1，学习率为0.005，时间步长为20 个交流电周期，细胞数为5个，对比结果如表2 所示。

表2 不同模型性能测试结果对比Table 2 Comparison of performance test results of different models

由表2 的测试结果可知，从准确率来看，RNN，LSTM 和SRU 模型的总体准确率均低于Bi-S-SRU模型，这是因为Bi-S-SRU 模型可结合双向数据信息，使评估结果更加接近真实情况。从训练时间来看，LSTM 为了解决RNN 中存在的梯度消失和梯度爆炸问题，提出了门控机制，导致其参数变多，训练时间增加；SRU 采用并行结构，有效降低了训练时间；Bi-S-SRU 在SRU 基础上进行了深度上的堆叠，因此在训练过程中，消耗的时间稍有增加。综上所述，Bi-S-SRU 评估模型具有较高的综合性能，能够快速且准确的给出电力系统暂态稳定预测结果。

4.3 暂态稳定预防控制结果分析

随机选择一个电力系统运行样本，基于Bi-SSRU 进行暂态稳定预测。该样本在预想故障1、故障2、故障4 和故障5 发生的情况下被预测为失稳样本，采用APSO 求解TSCOPF 来制定预防控制策略。在预想故障1 发生的情况下生成的预防性重调度策略如表3 所示，由表3 计算可得采取预防控制措施的总调节成本为1 871.59$。

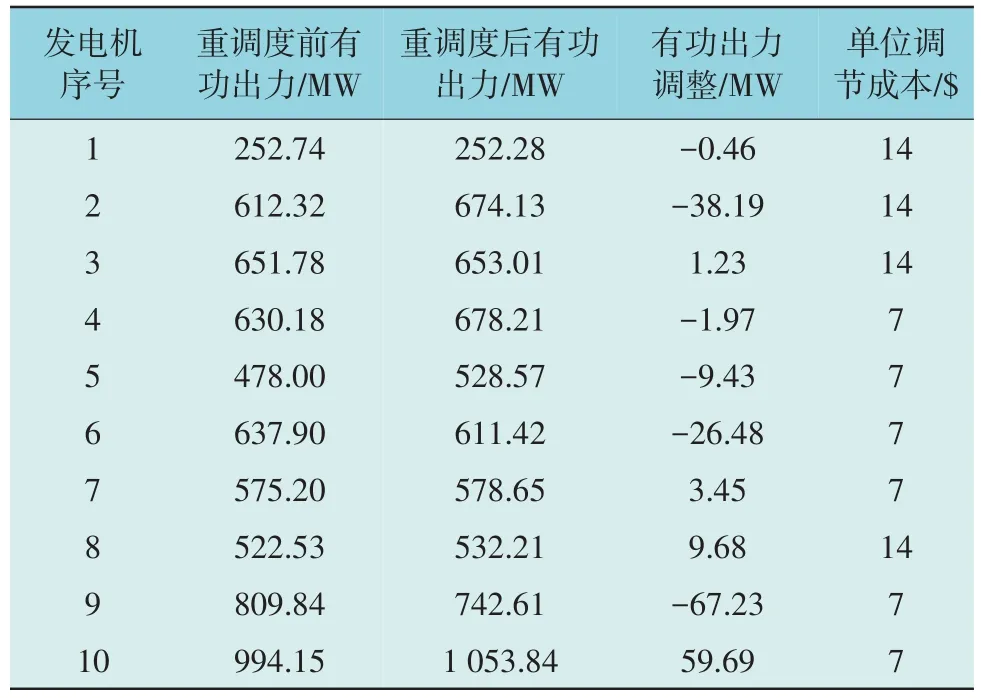
表3 预防控制的重调度策略Table 3 Rescheduling policy of preventive control

使用时域仿真验证基于APSO 给出的预防控制策略，计算故障下重调度前后电力系统ITS如表4 所示。

表4 重调度前后ITS 的比较Table 4 Comparisons of ITS before and after rescheduling

由表4 可以看出，当故障1、故障2、故障4 和故障5 发生时，系统会出现暂态失稳，采取预防控制策略后，系统将在故障发生后保持暂态稳定。当故障3、故障6 发生时，系统可以保持暂态稳定，在采取预防控制策略后，ITS均有所提高。因此，无论系统在预想故障情况下是否暂态失稳，采取基于APSO 给出的预防控制措施都可提高系统的暂态稳定性，将失稳情况调节为稳定，将稳定情况增强其稳定程度，由此证明了基于APSO 给出的预防控制策略能够有效提高系统暂态稳定性。

分别绘制故障1 和故障2 发生时IEEE 39 节点系统预防控制前后发电机功角曲线，如图3 和图4所示。

图3 故障1预防控制前后发电机功角轨迹Fig.3 Power angle trajectory of generator before and after preventive control of fault 1

图4 故障2预防控制前后发电机功角轨迹Fig.4 Power angle trajectory of generator before and after preventive control of fault 2

由图3、图4 可以看出，在预想故障发生时，电力系统有可能出现暂态失稳；在实施预防控制措施后，电力系统则保持暂态稳定。

5 结论

针对电力系统暂态稳定预防控制问题，本文提出了一种基于Bi-S-SRU 和APSO 的电力系统暂态稳定评估及预防控制策略方法。通过IEEE 39 节点系统上的算例分析，得到如下结论：

1）利用Bi-S-SRU 评估模型替代传统TSCOPF模型中的暂态稳定约束，避免了复杂的非线性微分代数方程计算，提高了计算效率，有利于实现在线应用。

2）与RNN，LSTM，SRU 模型相比，Bi-S-SRU 模型凭借其并行方式及深度堆叠结构，具有更高的评估准确率和较短的训练时间。

3）APSO 可以自适应调整粒子惯性权重，并增强粒子在初始阶段的全局搜索能力以及后期的局部寻优能力，得到最优解。