基于特征集成学习的四川省土壤厚度预测①
陈玉蓝,梁太波,张艳玲,王 勇,袁大刚,朱 俊,李德成
基于特征集成学习的四川省土壤厚度预测①
陈玉蓝1,梁太波2,张艳玲2,王 勇1,袁大刚3,朱 俊4*,李德成5
(1 四川省烟草公司凉山州公司,四川西昌 615000;2 中国烟草总公司郑州烟草研究院,郑州 450001;3 四川农业大学资源学院,成都 611130;4 南京工业职业技术大学计算机与软件学院,南京 210023;5 中国科学院南京土壤研究所,南京 210008)
以四川省土壤厚度预测为例,为农业生产与生态环境评价中土壤厚度空间分布图的编制提供方法支持。对比分析了随机森林、分位数回归森林、支持向量机、集成学习模型对连续型土壤厚度的预测精度,并提出了一种基于特征集成学习的土壤厚度类型预测算法。研究结果表明:①四川省土壤厚度具有较高的空间异质性,控制其空间变化的主要地形因子包括谷底平坦综合指数、高程与地形湿度指数;②四川省土壤厚度预测模型的决定系数为0.32 ~ 0.47,均方根误差为0.28 ~ 0.41 m;③面向连续型土壤厚度预测的集成模型具有较高的预测精度与稳健性,能够充分集成子模型的优势。特征集成学习能够有效集成并融合了连续型土壤厚度预测与离散型土壤厚度类型预测结果,通过减少方差来提高预测结果的稳健性。
数字土壤制图;机器学习;集成学习;四川省
土壤厚度是土壤质量评价、土壤碳库估算与水土保持最重要的物理指标之一[1]。土壤性质的垂直变异程度受到土壤厚度的直接影响,因此土壤厚度是土壤属性空间变化模拟乃至土壤时空变异特征研究的重要主题[2]。
通常情况下,土壤厚度是通过土壤剖面的调查来获得的。我国中西部山地地区道路可达性较差、面积较大,这就导致我国部分地区难以获得详实的土壤厚度调查数据。基于土壤–景观范式,数字土壤制图通过集成地理信息系统技术、遥感分析技术与计算机模拟技术来量化土壤属性的时空变异特征,已受到国内外土壤学界的普遍接受。目前,数字土壤制图的主流技术已从传统的地统计学发展为机器学习[3]。有别于其他土壤理化属性,土壤厚度与成土要素(例如气候、地形)的相关性较低,常规的机器学习算法预测性能往往不够理想。国内外学者对土壤厚度预测过程中的数据获取[4]、环境变量筛选[5-7]、预测模型改进[8-11]、预测不确定性分析[12-13]进行了探讨。相关研究表明,地形是预测土壤厚度最重要的环境变量之一[14],机器学习算法在表征土壤厚度空间变异方面具有较高的适宜性[6]。
在实际生产过程中,技术人员往往不太关心土壤厚度的准确数值,而更关注土体厚度是否能够满足特定的应用。例如,如果土壤剖面中A层与B层厚度之和大于60 cm,在不考虑地形对于水土流失影响的情况下,该土壤可能就适宜于农业生产。需要指出的是,野外调查获取到的土壤厚度数据往往基于挖掘或观察到的土壤剖面,受限于调查手段而无法获取到准确的土壤厚度信息,尤其是在土壤厚度大于2 m时。因此,获取准确的土壤厚度类型数据在实际应用上具有重要的意义。由于影响土壤厚度空间分布的环境变量种类较多,准确量化土壤厚度与环境变量之间的关系往往受到预测模型性能的影响,而且预测模型往往基于不同的理论假设,其预测结果在不同地形区的不确定性也不尽相同。因此,如何使用集成学习方法有机结合复杂景观区的预测模型,进而获得比单一种类预测模型更加优越的泛化性能是一个迫切需要解决的科学问题。
在前人已有相关工作的基础上,本文以四川省的土壤厚度预测为例,对比分析不同机器学习算法预测土壤厚度的精度,提出一种基于特征集成学习的土壤厚度预测方法,以提升土壤厚度空间预测的精度与稳健性。
1 材料与方法
1.1 研究区概况
四川省是我国的第五大省份,位于长江中下游平原和青藏高原地区的过渡带,地势西高东低,地形复杂多样,以山地为主,山地、丘陵约占全省面积的89%,这也导致了四川省土壤厚度空间变化的异质性较大。四川省绝大部分地区受季风环流影响,东部地区主要受东南季风控制,西部地区则主要受西南季风控制,因此四川省气候可以分为三大类,分别是川西北高山高原高寒气候、川西南山地亚热带半湿润气候与四川盆地中亚热带湿润气候。全省年平均气温7.97 ℃,平均日照1 830 h,平均年降水量858.32 mm。四川省的耕地面积为6.72万km2,林地面积为22.20万km2。按照中国土壤系统分类,四川省土壤类型主要是雏形土 (71%)、淋溶土(14%)与人为土(4%)。
1.2 土壤数据与环境变量
本文的土壤样本数据主要是四川省的土系调查[15](=195)与第二次全国土壤普查的数据[16](=99)(图1)。土系调查数据作为训练数据集用来训练预测模型,历史土壤数据作为独立验证数据集评估预测模型的精度。土系调查样点的布置主要考虑到交通可达性以及第二次土壤普查已采集样点的位置与气候、植被、母质、地形等成土因素的空间分布特征。土系调查样点的成土环境与发生层样品主要依据《野外土壤描述与采样手册》[17]进行描述,详细记录了各采样点的景观、剖面与新生体特写照片、成土条件描述、土壤剖面层次划分与各层次形态特征。
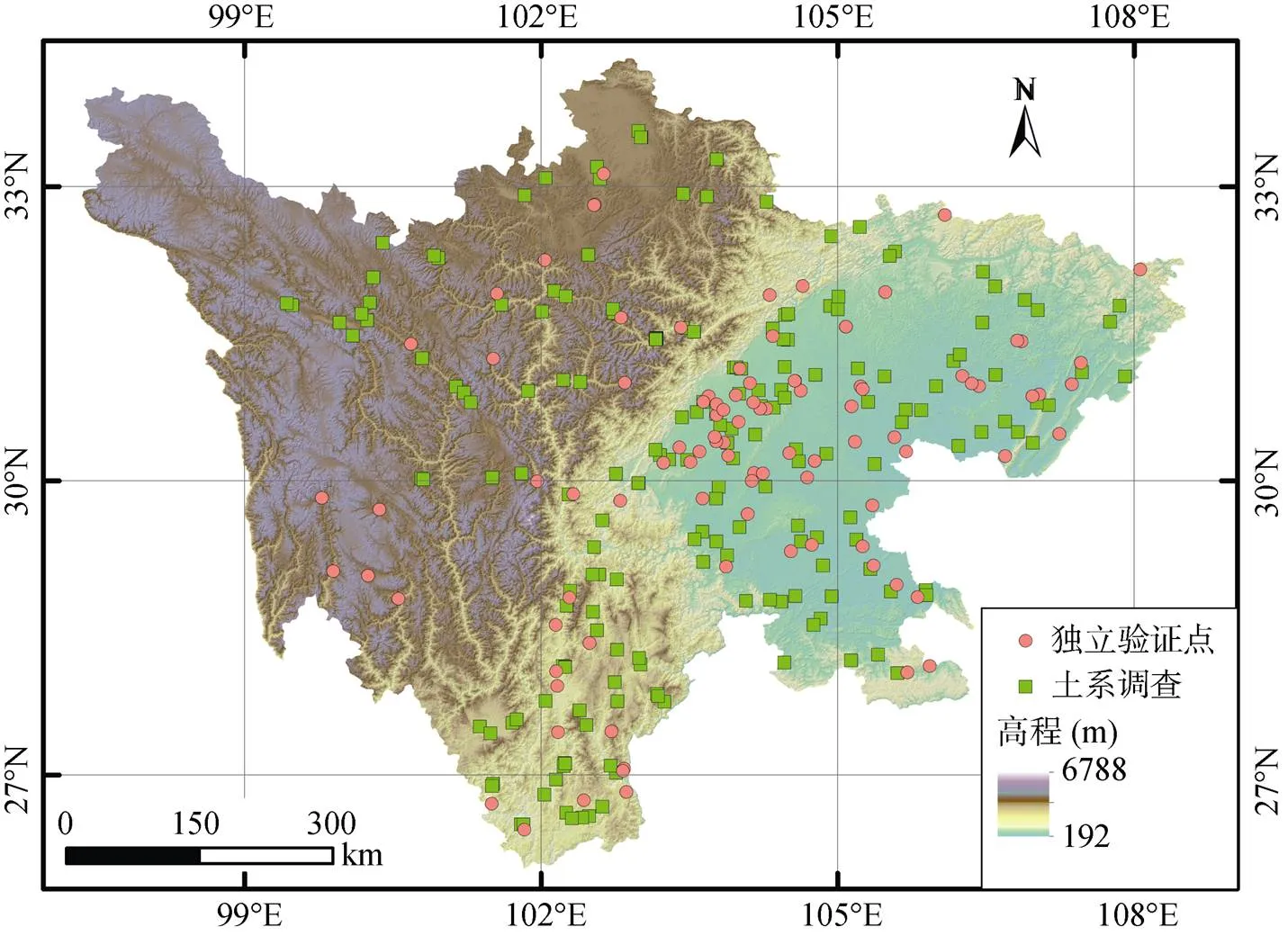
图1 四川省土壤采样点空间分布
本文共收集了17个环境变量(表1),包括地形因子、遥感因子、成土母质、土地利用。地形因子包括高程、坡向、坡度、平面曲率、剖面曲率、地形湿度指数等变量。气候变量包括年均气温、年均降雨。其他的变量包括土壤类型(土纲)、归一化植被指数、土地利用类型等。地形因子使用SRTM数据,遥感因子使用Landsat8数据,土地利用数据使用多年的平均值[18]。连续型环境变量使用Z-score方法进行标准化处理。
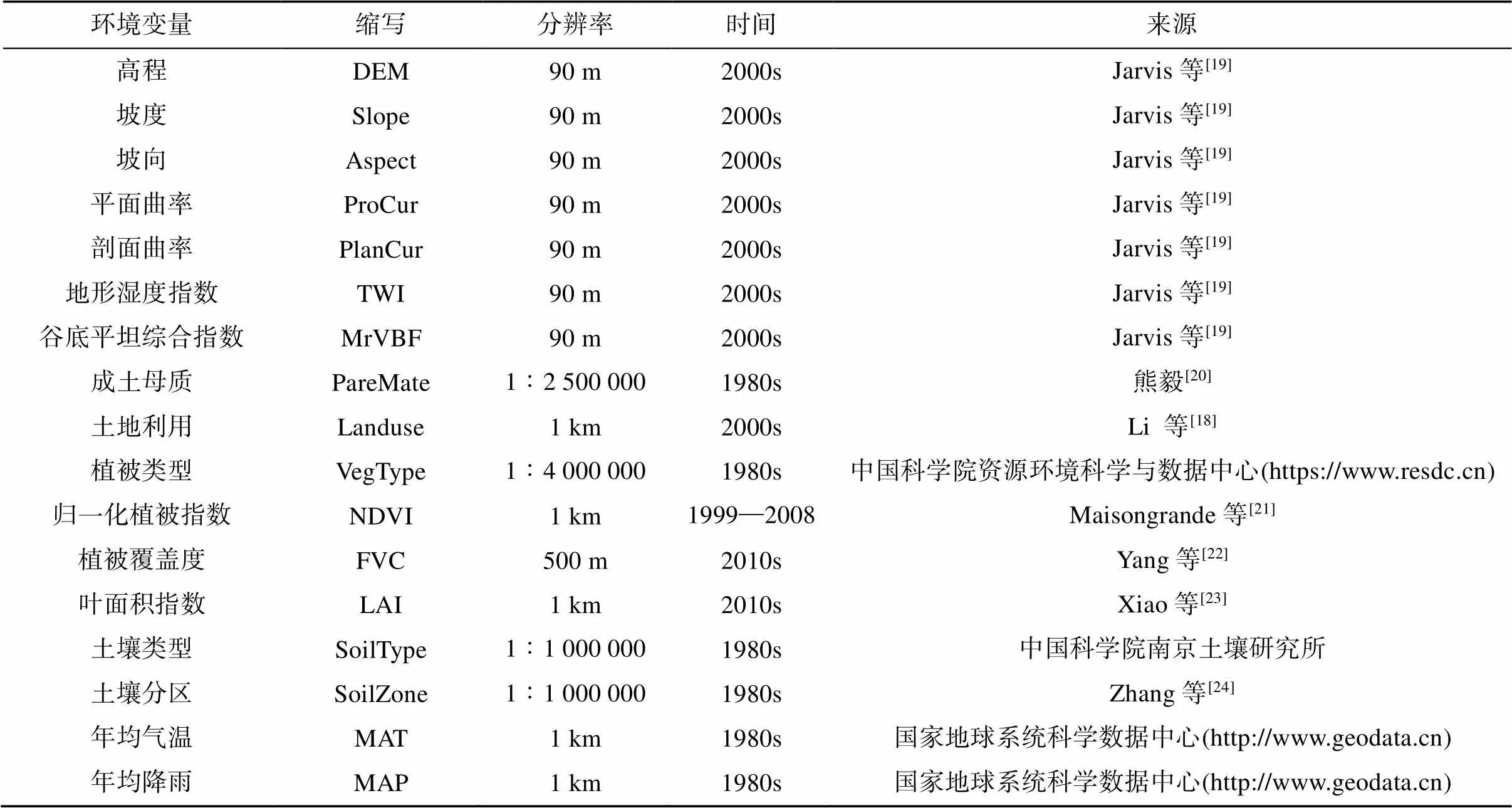
表1 环境变量介绍
1.3 土壤制图
传统研究将土壤厚度作为连续型的因变量。本文重点关注土壤厚度类型的空间分布规律及其主要驱动因素,提出一种基于特征集成学习的土壤厚度预测方法,将面向连续型土壤厚度的预测结果进行重分类,作为新的特征进行集成。具体的预测流程包括:
1) 使用机器学习算法预测连续型土壤厚度的空间分布。训练的机器学习算法包括:随机森林(Random Forest,RF)、分位数回归森林(Quantile Regression Forest,QRF)与支持向量机(Support Vector Machine,SVM)。
3) 对于上一步中的土壤厚度空间分布图进行重分类。由于本文土壤厚度数据较为有限(=195),考虑到土壤厚度数据的频率分布与土壤厚度预测精度对比的可操作性,将重分类的阈值设定为0 ~ 60 cm、60 ~ 100 cm与 >100 cm,对应的土壤厚度类型标识分别为1、2、3,该图层记为Depth1。如果研究区的土壤样点数据较多,也可以考虑划分更多的土壤厚度类型。
4) 基于训练数据集(=195),将采样点的土壤观测数据进行重分类,重分类的阈值为0 ~ 60、60 ~ 100 与>100 cm,对应的土壤厚度标识分别为1、2、3。使用随机森林、分位数回归森林与支持向量机算法分别进行土壤厚度类型的预测,筛选出预测精度最高的预测模型,并使用该方法预测四川省的土壤厚度类型空间分布图Depth2,分类精度为cla。因为因变量不同,该步骤与步骤2是完全独立的。
5) 使用特征集成机制,将两类土壤厚度类型空间分布图进行集成:
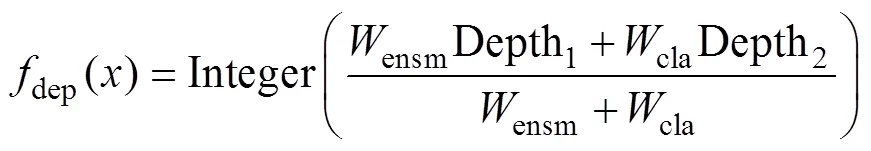
式中:ensm、cla分别是步骤2中连续型土壤厚度集成模型的预测精度和步骤4中离散型土壤厚度类型的预测精度。最终的预测结果采用四舍五入的方式生成土壤厚度类型的空间分布图。
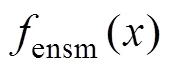
2 结果与分析
2.1 统计分析
采集的土壤厚度统计信息如表2、表3所示。根据《中华人民共和国水土保持法》[30],在5°以上地区的坡地植树造林、抚育幼林等需要采取水土保持措施,本文以5° 为阈值对采样点的土壤厚度进行了统计(表2)。方差分析结果表明冲积物、洪积物、泥岩成土母质条件下的土壤厚度呈现显著性差异(<0.05),不同土地利用、土壤类型条件下土壤厚度也呈现显著性差异(表3)。这说明四川省土壤厚度具有较高的空间异质性,需要综合考虑多种成土因素对土壤厚度的影响。
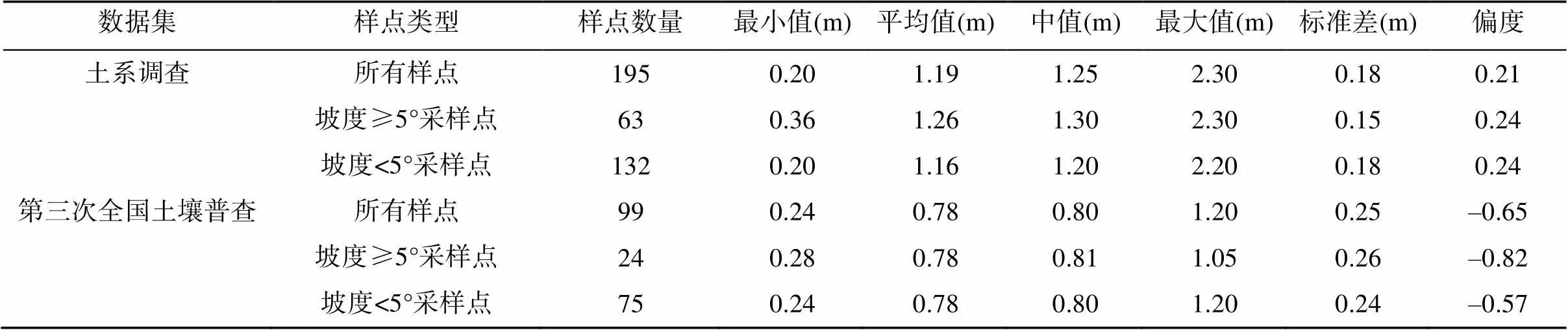
表2 采样点土壤厚度统计结果
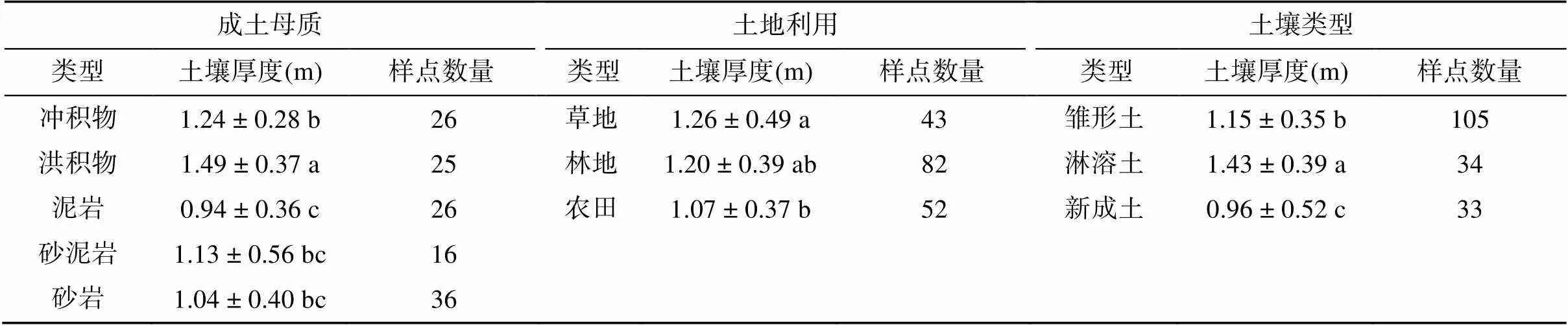
表3 不同成土母质、土地利用与土壤类型条件下土壤厚度(基于土系调查数据)
注:同列数据小写字母不同表示差异达<0.05显著水平。
2.2 模型训练与预测精度
由于收集的环境变量间具有一定的相关性,为了避免多重共线性问题,本文使用逐步回归方法选择最优自变量集合,并计算筛选环境变量的方差膨胀因子(Variance Inflation Factor,VIF),移除VIF》5的环境变量。使用随机森林模型量化了不同环境变量对于土壤厚度空间变异的表征能力(图2)。分析结果表明:气候因子、地形因子与植被指数被遴选为最有效的环境变量,其中地形因子(谷底平坦综合指数、高程与地形湿度指数)能够较好地表征土壤厚度的空间变异。
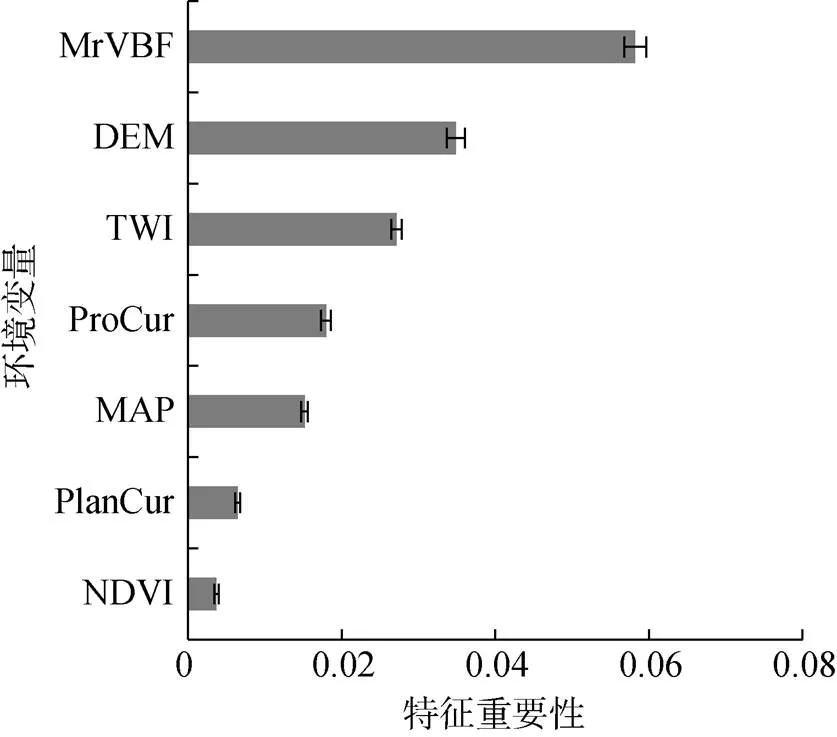
图2 基于随机森林的环境变量重要性
在独立执行100次试验之后,子模型与集成模型预测连续型土壤厚度的预测精度平均值如表4所示。总体上,子模型与集成模型的标准误差均接近0,随机森林与分位数回归森林的预测精度较为接近,均略高于支持向量机。集成模型的精度较子模型略有提升(2=0.47)。将土壤厚度样点数据进行重分类后构建分类预测模型,使用独立验证数据集对不同的预测模型进行精度评价(表5),结果表明特征集成模型的预测精度显著高于子模型与基于连续型土壤厚度的集成模型。使用独立验证数据的平均值作为预测结果,获取到的预测精度(分类精度)为0.29,特征集成模型的预测精度是以平均值作为预测结果的2.1倍(表5),本文提出的预测方法显著优于各子模型与以平均值作为预测结果的精度。
2.3 土壤厚度空间分布
基于3种机器学习与集成学习预测的土壤厚度值空间分布如图3所示。3种子模型与集成学习模型预测的平均土壤厚度基本一致(1.17 ~ 1.19 m),预测的土壤厚度最小值为0.36 m,最大值为2.10 m(表6)。集成学习预测结果的标准差比其他3种子模型的预测结果小,说明集成学习模型具有较高的稳健性。宏观分布上,成都平原、川西高原呈现截然不同的土壤厚度空间分布特征,这主要归因于地形地貌对于土壤厚度的影响。成都平原虽然属于四川盆地内的平原,但是其平均厚度远大于1 m。川西高原地形起伏大,自然条件复杂,土壤形成过程也复杂多变,因此该地区的土壤厚度具有极高的空间异质性。
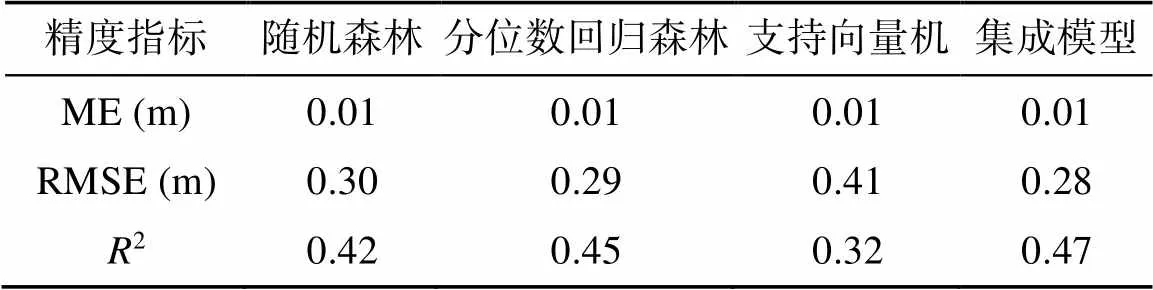
表4 面向连续型土壤厚度子模型与集成模型的预测精度(基于土系调查数据)

表5 面向土壤厚度类型子模型与集成模型的预测精度(基于独立验证数据)
使用分位数回归森林预测的90% 置信区间来分析预测结果的不确定性(图4)。连续型土壤厚度的5%分位数与95% 分位数(图4)与其他预测结果呈现类似的空间分布特征,也即土壤厚度自西向东呈现逐步下降的趋势。山地区域,尤其是四川盆地至川西高山高原区过渡区域土壤厚度的空间预测不确定性较高,说明在山地区域需要收集更多的土壤样点来降低预测结果的不确定性。基于预测的连续型土壤厚度(图3D)、子模型(分位数回归森林)预测的土壤厚度类型与预测精度,生成最终的土壤厚度类型空间分布图(图5),其中<0.6、0.6 ~ 1.0和>1.0 m 3种类型的面积百分比分别为5.6%、31.4% 和63.0%。

表6 不同预测算法预测土壤厚度的统计结果
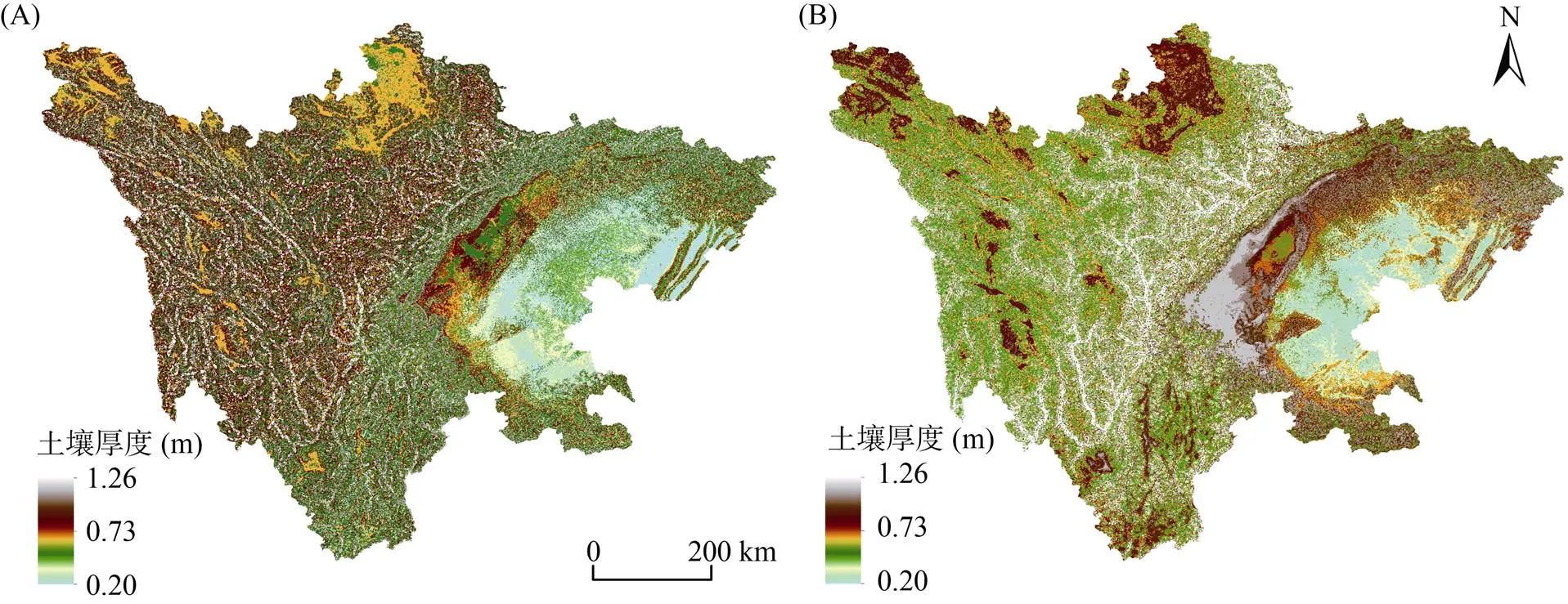
(A. 5%分位数;B. 95%分位数)
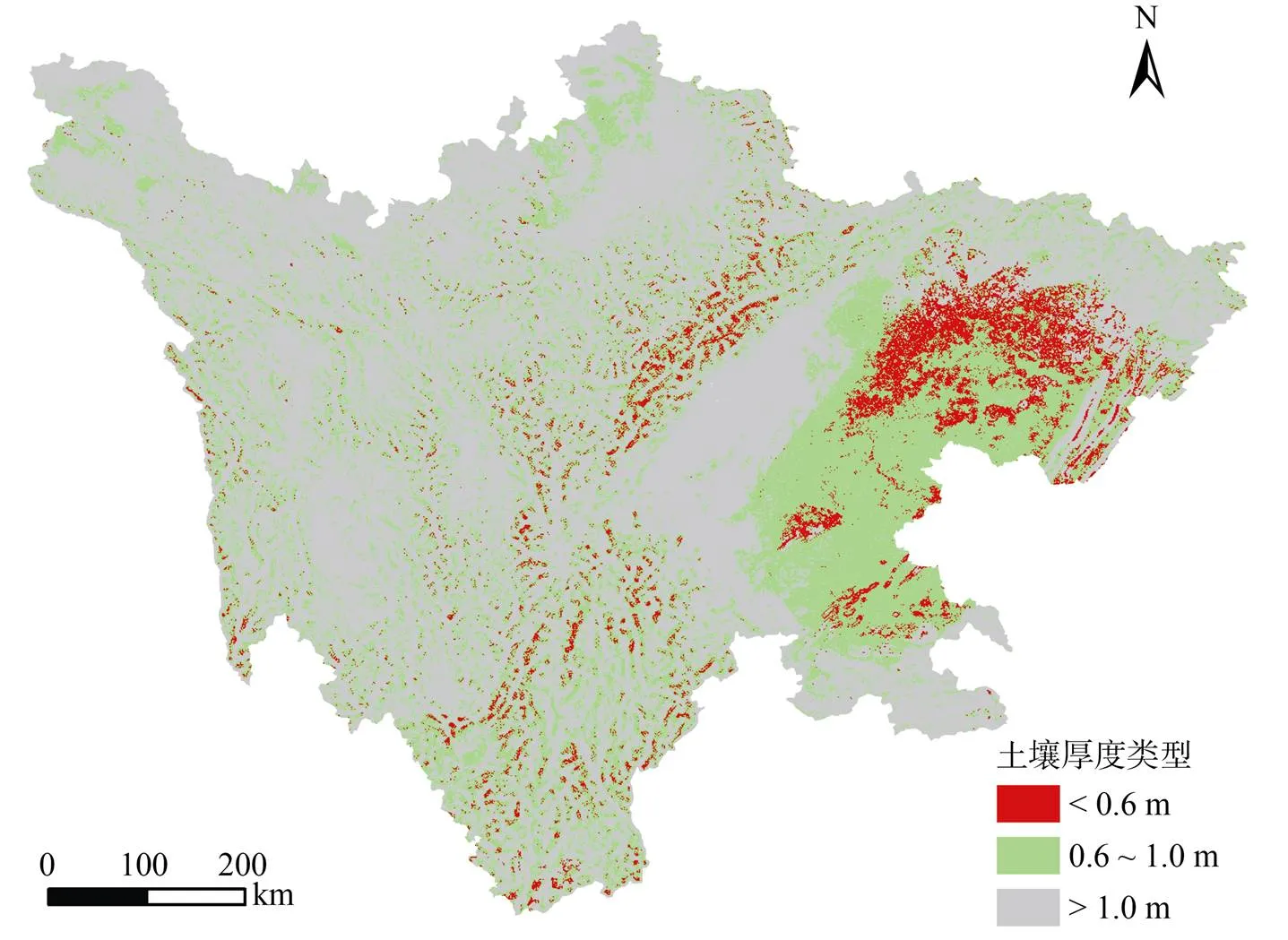
图5 基于集成学习生成的土壤厚度类型空间分布
3 讨论
土壤厚度是指导农业生产与生态环境评价的重要基础信息,然而传统的土壤调查仅能获取采样点的土壤厚度数据,难以获取土壤厚度的空间分布图层。本文使用基于权重的机器学习模型,针对地形复杂的平原与山地地貌区域提出了一种基于特征集成学习的土壤厚度预测算法,该算法充分利用了集成学习能够充分结合多个机器学习算法的优点,并融合了连续型土壤厚度预测与离散型土壤厚度类型预测结果,通过减少方差来提高预测结果的稳健性。在前期的预试验过程中,也尝试了人工神经网络、普通克里格、多元线性回归方法,但是这些子模型的精度比本文使用的3种机器学习算法精度低。在提出的特征集成学习的框架下,用户可以根据需求遴选不同数量、不同种类的子模型。由于土壤厚度数据有限,本文使用历史土壤数据作为独立验证数据集评估预测模型的精度。有别于其他土壤属性,土壤厚度随时间的推移变化较小,而且本研究中土壤厚度类型分类阈值跨度较大(0 ~ 60 cm、60 ~ 100 cm与>100 cm)。尽管验证数据集与建模数据集的采样时间相差30多年,历史土壤厚度数据的使用并未影响本文的独立验证。
有别于以往的集成学习模型,本文提出的方法使用子模型进行土壤厚度类型预测,这主要是考虑到机器学习算法在构建回归与分类预测模型上的差异性。同时,需要特别指出的是,与常规的土壤理化属性不同,土壤厚度一般为实际观测到的最大采样深度,这取决于调查人员挖掘剖面的实际调查深度,因此使用土壤厚度分类机制能够较好地表征土壤类型的空间分布特征,避免给出不够准确的土壤厚度信息。尽管独立验证数据集平均值略低于建模样点(表2),但是模型预测精度评价结果表明特征集成模型能够较好地预测土壤厚度类型的空间分布(表5)。
在实际的土壤调查过程中,土壤厚度往往只记录了观测数据,事实上的土壤厚度可能远远大于实际的观测值[1],这种“不准确的”土壤厚度观测数据会给预测模型带来一定的预测误差,导致部分地区的土壤厚度出现严重的低估情况。针对这种情况,国内外也有部分学者将土壤厚度定义为删失数据(right censored data)[12],并构建了随机生存森林来预测超过一定土壤厚度阈值概率的空间分布。分析预测的土壤厚度的宏观分布特征(图3、图4)可以发现,土壤厚度与地形因子之间绝非简单的线性关系,而是存在十分复杂的非线性关系。地统计模型需要满足空间自相关假设条件,而土壤厚度在不同地形条件下呈现迥异的分布特征(图3),因此本文未考虑使用地统计技术作为对比模型。
基于随机森林的变量重要性分析仅能量化环境变量对土壤厚度空间变异的表征能力,不能给出具体的驱动作用的解释。由于土壤演化受到多种成土因素的长期综合作用,因此土壤厚度的主要驱动因素也复杂多样。方差分析结果显示土壤厚度在不同的土壤类型、成土母质条件下呈现显著性差异(表3),但是环境变量筛选过程却剔除了这些分类变量。因此,在现有筛选的环境变量集的基础上(图2)增加了这些分类变量并测试了模型的预测精度。结果表明,无论是增加一个分类变量还是多个分类变量,集成模型的预测精度均没有显著提升(>0.05)。这可能是由于表3中的环境变量信息是基于野外调查的结果,而收集到的覆盖整个研究区的分类变量的精度与分辨率还不足以表征土壤厚度的空间变异特征。
总体上,本文连续型土壤厚度预测模型的决定系数为0.47(表4),比相关研究在区域尺度(0.16 ~ 0.34)与国家尺度(0.11 ~ 0.41)的预测准确度高[10, 13],这说明本文使用的环境变量能够较好地表征土壤厚度的空间变化特征,拟合的预测模型能够准确地量化土壤–景观关系。例如,地形湿度指数通常在靠近流域网络的区域值较高,这些区域比其他区域具有更多的河流冲积物,因此其土壤厚度也可能比其他地区高,地形湿度指数能够较好地表征山地区域土壤厚度的空间分布特征[9]。Ryland等人[4]在约16 hm2的Calhoun地球关键带观测站使用电磁感应设备(Dualem-21S EMI)调查了3.7万个观测点,并使用地统计方法获得了该地区土壤黏化层的厚度空间分布图。该研究指出坡底由于受到更严重的土壤侵蚀而具有较浅的冲积物,这也说明土壤厚度空间预测模型的准确拟合需要足够土壤数据的支持。
4 结论
1) 四川省土壤厚度具有较高的空间异质性,难以使用单一的成土要素进行量化。
2) 地形因子(谷底平坦综合指数、高程与地形湿度指数)能够较好地表征山地区土壤厚度的空间变异特征。
3) 面向连续型土壤厚度预测的集成模型具有较高的预测精度与稳健性,能够充分集成子模型的优势。特征集成学习能够有效集成并融合了连续型土壤厚度预测与离散型土壤厚度类型预测结果,通过减少方差来提高预测结果的稳健性。
但由于研究区较大,样本数据有限,本文提出的算法还需要在收集到更多的土壤数据或类似的研究区进行完善。
[1] 易晨, 李德成, 张甘霖, 等. 土壤厚度的划分标准与案例研究[J]. 土壤学报, 2015, 52(1): 220–227.
[2] 张甘霖, 史舟, 朱阿兴, 等. 土壤时空变化研究的进展与未来[J]. 土壤学报, 2020, 57(5): 1060–1070.
[3] Wadoux A M J C, Minasny B, McBratney A B. Machine learning for digital soil mapping: Applications, challenges and suggested solutions[J]. Earth-Science Reviews, 2020, 210: 103359.
[4] Ryland R C, Thompson A, Sutter L A, et al. Mapping depth to the argillic horizon on historically farmed soil currently under forests[J]. Geoderma, 2020, 369: 114291.
[5] Lu Y Y, Liu F, Zhao Y G, et al. An integrated method of selecting environmental covariates for predictive soil depth mapping[J]. Journal of Integrative Agriculture, 2019, 18(2): 301–315.
[6] Horst-Heinen T Z, Dalmolin R S D, ten Caten A, et al. Soil depth prediction by digital soil mapping and its impact in pine forestry productivity in South Brazil[J]. Forest Ecology and Management, 2021, 488: 118983.
[7] Wang Q, Wu B F, Stein A, et al. Soil depth spatial prediction by fuzzy soil-landscape model[J]. Journal of Soils and Sediments, 2018, 18(3): 1041–1051.
[8] Penížek V, Borůvka L. Soil depth prediction supported by primary terrain attributes: A comparison of methods[J]. Plant, Soil and Environment, 2006, 52(9): 424–430.
[9] Wu S W, Lin C Y, Sun M Y, et al. Estimation of soil depth in the Liukuei Experimental Forest by using conceptual model[J]. CATENA, 2022, 209: 105839.
[10] Dharumarajan S, Vasundhara R, Suputhra A, et al. Prediction of soil depth inusing digital soil mapping approach[J]. Journal of the Indian Society of Remote Sensing, 2020, 48(11): 1593–1600.
[11] 王改粉, 赵玉国, 杨金玲, 等. 流域尺度土壤厚度的模糊聚类与预测制图研究[J]. 土壤, 2011, 43(5): 835–841.
[12] Chen S C, Mulder V L, Martin M P, et al. Probability mapping of soil thickness by random survival forest at a national scale[J]. Geoderma, 2019, 344: 184–194.
[13] Chen S C, Richer-de-Forges A C, Leatitia Mulder V, et al. Digital mapping of the soil thickness of loess deposits over a calcareous bedrock in central France[J]. Catena, 2021, 198: 105062.
[14] 于全波, 张浪, 黄绍敏, 等. 城镇搬迁地土壤厚度划分与案例研究[J]. 土壤, 2021, 53(5): 1081–1086.
[15] 张甘霖, 袁大刚. 中国土系志·四川卷[M]. 北京: 科学出版社, 2020.
[16] 全国土壤普查办公室. 中国土种志·第六卷[M]. 北京: 中国农业出版社, 1996.
[17] 张甘霖, 李德成. 野外土壤描述与采样手册[M]. 北京: 科学出版社, 2022.
[18] Li X C, Yu L, Sohl T, et al. A cellular automata downscaling based 1 km global land use datasets (2010—2100)[J]. Science Bulletin, 2016, 61(21): 1651–1661.
[19] Jarvis A, Reuter H I, Nelson A, et al. Hole-filled SRTM for globe (Version 4)[OL]. 2018-11-01(2023-07-04). http:// srtm.csi.cgiar.org.
[20] 熊毅主编. 王鹤林, 黄翠琴编绘. 中国土壤图集[M]. 北京: 地图出版社, 1986.
[21] Maisongrande P, Duchemin B, Dedieu G. VEGETATION/ SPOT: An operational mission for the Earth monitoring; presentation of new standard products[J]. International Journal of Remote Sensing, 2004, 25(1): 9–14.
[22] Yang L Q, Jia K, Liang S L, et al. Comparison of four machine learning methods for generating the GLASS fractional vegetation cover product from MODIS data[J]. Remote Sensing, 2016, 8(8): 682.
[23] Xiao Z Q, Liang S L, Jiang B. Evaluation of four long time-series global leaf area index products[J]. Agricultural and Forest Meteorology, 2017, 246: 218–230.
[24] Zhang G L, Song X D, Wu K N. A classification scheme for Earth’s critical zones and its application in China[J]. Science China Earth Sciences, 2021, 64(10): 1709–1720.
[25] Brungard C, Nauman T, Duniway M, et al. Regional ensemble modeling reduces uncertainty for digital soil mapping[J]. Geoderma, 2021, 397: 114998.
[26] Song X D, Wu H Y, Ju B, et al. Pedoclimatic zone-based three-dimensional soil organic carbon mapping in China[J]. Geoderma, 2020, 363: 114145.
[27] Meyer D, Dimitriadou E, Hornik K, et al. e1071: Misc functions of the department of statistics, probability theory group (Formerly: E1071), TU Wien[OL]. 2023-02-01 (2023-07-04). https://CRAN.R-project.org/package=e1071.
[28] Liaw A, Wiener M. Classification and regression by randomForest[J]. R News, 2002, 2(3): 18–22.
[29] Meinshausen N. quantregForest: Quantile Regression Forests[OL]. 2017-12-19 (2023-07-04). https://CRAN.R- project.org/package=quantregForest.
[30] 刘志仁, 王嘉奇. 黄河流域中上游水土保持法律制度研究[J]. 干旱区资源与环境, 2022, 36(11): 10–18.
Spatial Prediction of Soil Thicknesses in Sichuan Province Based on Feature-Ensemble Learning
CHEN Yulan1, LIANG Taibo2, ZHANG Yanling2, WANG Yong1, YUAN Dagang3, ZHU Jun4*, LI Decheng5
(1 Liangshan Branch of Sichun Tobacco Company, Xichang, Sichuan 615000, China; 2 Zhengzhou Tobacco Research Institute of CNTC, Zhengzhou 450001, China; 3 College of Resources, Sichuan Agricultural University, Chengdu 611130, China; 4 School of Computer and Software, Nanjing Vocational University of Industry Technology, Nanjing 210023, China; 5 Institute of Soil Science, Chinese Academy of Sciences, Nanjing 210008, China)
This study compared the prediction accuracy of random forest, quantile regression forest, support vector machine and ensemble learning in mapping soil thickness taken as a continuous variable, where the machine learning models were weighted as individual models. Furthermore, a feature-ensemble learning algorithm was proposed for mapping soil thickness, in which soil thicknesses was classified as a new categorical variable, and the discrete predictions were further weighted with the predicted continuous soil thicknesses.The results showed that soil thicknesses in Sichuan Province were characterized with high spatial variation, of which the dominated drivers included multiresolution index of valley bottom flatness, elevation and topographic wetness index. The overall performance of prediction models in terms of coefficients of determinations and root mean square errors were 0.32–0.47 and 0.28–0.41 m, respectively. For the prediction of continuous soil thickness, ensemble models had low errors than those of individual models. For soil thickness types, the proposed feature-ensemble learning algorithm achieved higher robustness than other considered models by reducing the variance of prediction.
Digital soil mapping; Machine learning, Ensemble learning; Sichuan Province
S158.3
A
10.13758/j.cnki.tr.2023.04.024
陈玉蓝, 梁太波, 张艳玲, 等. 基于特征集成学习的四川省土壤厚度预测. 土壤, 2023, 55(4): 894–902.
中国烟草总公司四川省公司科技项目(SCYC202103)、中国烟草总公司重点研发项目(110202102038)和南京工业职业技术大学引进人才科研启动基金项目资助。
(zj_zijin@163.com)
陈玉蓝(1990—),女,四川宜宾人,博士研究生,主要研究领域为土壤肥料。E-mail: 369507968@qq.com

