旋翼翼型流动分离特性分析及高升力设计

王雪鹤,张子瀚,柴春硕,邢世龙,袁明川

(中国直升机设计研究所 直升机动力学全国重点实验室,江西 景德镇 333001)

0 引言

旋翼作为直升机重要的动部件,影响着直升机的飞行性能。对配置在旋翼上的翼型进行针对性设计,能够使旋翼气动性能得到直接的提升。然而,直升机旋翼面临的气动环境十分复杂,设计指标分解到旋翼翼型上后,在较宽速度范围和升力系数范围对其气动性能有着近乎苛刻的性能要求。根据传统的翼型设计指标要求,旋翼翼型需要具备较高的最大升力(clmax)以满足前飞和机动性能,较高的阻力发散马赫数(Madd)以满足前飞性能,较低的阻力系数(cd)以满足前飞和悬停性能,较低的力矩系数(cm)以满足操纵性能[1]。在上述设计指标中,最大升力性能是旋翼翼型设计中不可妥协的一个重要性能指标。如法国ONERA设计的OA系列旋翼翼型,在每代设计指标中均对clmax提出了要求[2];俄罗斯设计的多代TsAGI旋翼翼型,有朝着“更高的clmax、更高的Madd”发展的趋势[3]。因此,对失速特性的研究和提高最大升力系数成为旋翼翼型设计的重要方向之一。

在翼型失速机理分析方面,国外Katarzyna Surmac[4]采用风洞试验和CFD的方法,对SSC-A09翼型的失速后的流场特性进行了专门的分析,CFD计算结果和油流显示结果表现出了良好的一致性,均在大攻角时观察到上表面分离涡的出现。国内有文献[5]阐述了翼型流动分离的三种类型,但文中没有涉及分离流场的动态变化。有关翼型失速的流动机理分析常见于翼型动态特性研究的相关文献[6]中。但从旋翼翼型设计的角度,首先关注的是静态失速特性[7],因此需要设计人员对旋翼不同剖面的旋翼翼型静态失速特性具有深入的认识。

文献[5]总结了国外设计人员提高固定翼翼型最大升力的方法,概括起来主要是采用了较大的前缘半径和后部弯度。但对于旋翼翼型,较大的前缘半径会导致高马赫数阻力和阻力发散马赫数激增;较大的弯度也会导致较高的低头力矩。上述方法无法很好地满足旋翼翼型设计要求。国内研究人员在旋翼翼型设计方面,大多通过数值优化手段将最大升力作为优化目标之一。孙俊峰等[8]采用基于进化算法的多目标优化方法和Kriging代理模型,分别将0.3Ma、0.4Ma、0.5Ma的最大升力系数作为优化目标之一,对OA309翼型进行了优化设计,得到增升减阻的翼型结果;杨慧等[9]采用基于Kriging代理模型的优化算法,将0.4Ma最大升力系数作为优化目标之一,对OA209翼型开展了多目标优化设计。尽管采用数值优化方法可以得到满足最大升力目标的翼型结果,但在设计过程中,由于缺少对提高旋翼翼型最大升力的机理认识,优化结果对工程设计的指导意义有限。

本文选取两种具有代表性厚度的旋翼翼型,开展旋翼翼型流动分离特性数值模拟分析,旨在揭示不同厚度翼型的失速特性及流动机理,并据此开展旋翼翼型失速特性参数影响研究。

1 数值模拟方法及验证

1.1 流动控制方程

在连续介质的假设下,忽略彻体力和热源,二维可压缩非定常N-S(Navier-Stokes)方程的表达式如下:

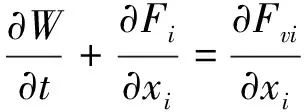
(1)

式中

式中,ρ为流体密度,ui为流体速度,p为压力,E为单位质量总能,τij为粘性应力张量,δij为克罗尼柯尔符号。

为较好地模拟翼型大攻角分离流动,本文采用Menter[10]发展的k-ωSST模型对控制方程进行封闭。

1.2 NACA0012翼型流场求解

为验证本文采用的数值模拟方法,首先对NACA0012翼型的流场进行求解,并与试验结果对比。经过网格收敛性研究(粗、中、密网格量分别为1.48万、2.79万、5.4万),采用网格量为2.79万的O型网格进行CFD计算,网格第一层高度5×10-6,远场为50倍弦长,如图1所示。

图1 NACA0012翼型CFD计算网格

图2给出了Ma=0.3,Re=6×106条件下NACA0012翼型在不同攻角下的压力分布定常计算结果与试验结果[11]的对比。压力分布计算结果与试验数据吻合良好。

图2 NACA0012翼型压力分布计算与试验结果对比(Ma=0.3,Re=6×106)

图3给出了NACA0012翼型在Ma=0.15,Re=6×106时的升、阻力系数定常计算结果与试验数据[12]的对比,并补充了失速攻角附近的非定常计算结果。考虑到翼型失速后,试验结果本身受三维效应的影响较大,因此最大升力系数的计算值与试验数据存在差别,不过两者的失速攻角十分接近。

图3 NACA0012翼型升、阻力计算与试验结果对比(Ma=0.15,Re=6×106)

总体上,CFD计算结果与试验数据吻合良好,验证了本文采用的数值模拟方法的可靠性。

2 OA212翼型流动分离特性分析

采用定常RANS方法计算OA212翼型在不同攻角下的流场,计算状态为Ma=0.3,Re=6×106,获得力系数曲线,如图4所示。定常计算结果显示,翼型在15°攻角之后失速。

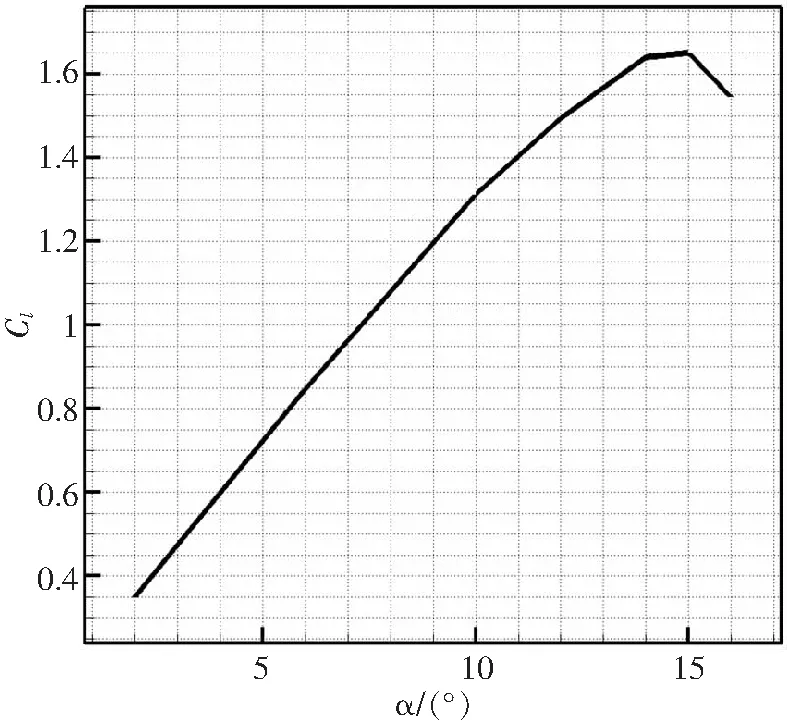
图4 OA212翼型升力系数定常计算结果(Ma=0.3,Re=6×106)

由于失速攻角附近翼型绕流出现分离流动,为模拟流动分离后流场的变化情况,本文在翼型失速攻角附近采用非定常计算方法求解翼型的流场。计算时间步长取0.002 s,时间步数取1000步,获取翼型在2 s时间内的瞬时流场。

图5、图6分别给出了OA212翼型在16°、18°攻角的瞬态流场。可以看到,OA212翼型在攻角为16°时,后缘分离区域在0.4 s后即形成稳定的分离涡形态;随着攻角增加到18°,后缘分离区域向前缘扩展,但依旧能够保持稳定的涡结构。

图5 OA212翼型16°攻角瞬态流场

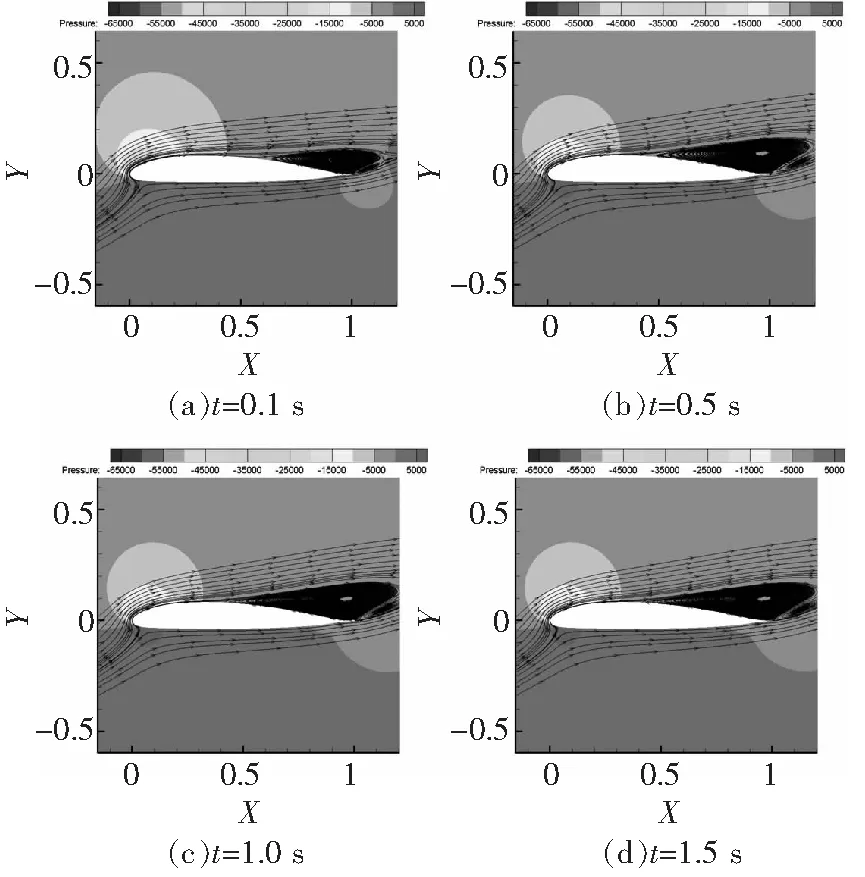
图6 OA212翼型18°攻角瞬态流场(Ma=0.3,Re=6×106)

从失速形态可以看出,OA212翼型的失速由后缘分离开始;随攻角增加,分离区域向前缘扩展;分离过程相对稳定,对应着和缓的失速现象。

3 OA206翼型流动分离特性分析

采用定常RANS方法计算OA206翼型在Ma=0.3,Re=6×106的力系数曲线,从曲线结果中判断失速攻角在9°附近,如图7所示。其中,由于失速后受非定常分离流动的影响,10°攻角的升力系数值取迭代过程中的平均值。

图7 OA206翼型升力系数定常计算结果(Ma=0.3,Re=6×106)

图8、图9分别给出了OA206翼型在9°、10°攻角的瞬态流场。9°攻角时,翼型表面始终维持着附着流动。但当增加到失速攻角10°后,从图9中可以看到,流动从0.14 s开始前缘出现明显的分离涡,然后分离区域扩大并向后移动,直至分离涡脱落;0.42 s时前缘再次形成分离涡,上表面的分离涡表现出周期性脱落的性质。与OA212翼型不同,OA206翼型分离涡脱落的过程使得翼型上表面阶段性地处于大范围分离状态,翼型的升阻力和力矩变化剧烈,表现出明显的非定常特性。

图8 OA206翼型9°攻角瞬态流场(Ma=0.3,Re=6×106)

图9 OA206翼型10°攻角瞬态流场(Ma=0.3,Re=6×106)

常规直升机旋翼桨尖处薄翼型在后行侧的来流马赫数常在0.4以上,因此增加OA206翼型0.4Ma的失速流场分析。通过静态计算结果判断,翼型此状态下在8°攻角后失速,此处不再赘述。

图10和图11分别给出了OA206翼型在Ma=0.4,Re=6×106时8°、9°攻角的瞬态流场。在8°攻角时,翼型前缘附近出现小分离泡,但始终维持在前缘,并未向后扩展,因而此时翼型并未失速。在9°攻角时,OA206翼型出现了周期性的涡脱落,非定常特性显著。

图10 OA206翼型8°攻角瞬态流场(Ma=0.4,Re=6×106)

图11 OA206翼型9°攻角瞬态流场(Ma=0.4,Re=6×106)

4 流动机理分析

提取OA212、OA206翼型在0.3Ma失速前的压力分布及压力梯度信息,分别如图12和图13所示。

图12 OA212、OA206翼型失速前上表面前缘附近压力分布对比(Ma=0.3,Re=6×106)

图13 OA212、OA206翼型失速前上表面前缘附近压力梯度对比(Ma=0.3,Re=6×106)

由于薄翼型前缘半径较小,流动在靠近上表面前缘附近很短一段范围内经历了“流动加速使负压达到峰值、强逆压梯度使压力恢复”的过程,空气压缩性较强,流动难以维持附着状态,在前缘附近发生分离,再附后形成涡结构,向后缘移动并周期性脱落。

对厚翼型来说,尽管进入失速状态前在前缘同样有着较高的负压峰值,但负压增长的速度相对缓慢,且经过翼型前部外形曲率起到的气流加速作用,故而上表面压力分布不但梯度更小,而且峰值点向后延伸了一段距离,有效缓解了前缘的气流分离趋势。

由于曲率变化相对更大,厚翼型在上表面较大的范围内均面临着更强的逆压梯度,如图14所示。翼型后缘气流在逆压梯度的作用下,最终难以维持附着流动而发生后缘分离。厚翼型的流动分离是一种从后缘向前缘发展的相对稳定的过程,一般情况下不具备在前缘诱发分离的条件。

图14 OA212、OA206翼型失速前上表面中后段压力梯度对比(Ma=0.3,Re=6×106)

5 旋翼翼型失速特性参数影响分析

5.1 OA212翼型失速特性参数影响分析

根据前文分析内容可知,12%相对厚度的翼型,失速由后缘分离起始。升力的降低主要由后缘分离涡导致。提高最大升力应该主要从如何抑制后缘分离流动入手。

在OA212翼型的基础上,增加前部(约0.1倍弦长处)曲率,降低前缘负压峰值的同时抬高前部压力曲线;在后缘流动分离区域(0.8倍弦长处),增加翼型局部曲率,减小翼型后缘的反弯度。修改后的外形和压力分布对比如图15、图16所示。

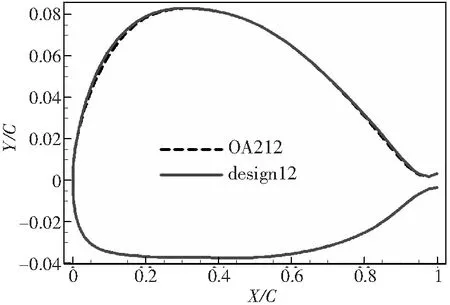
图15 12%厚度翼型设计前后外形对比

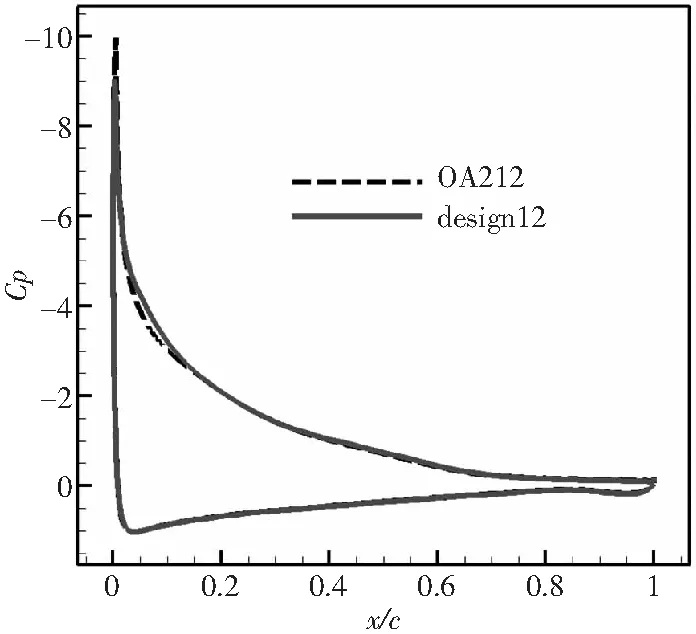
图16 12%厚度翼型高升力设计前后压力分布对比(α=15°,Ma=0.3,Re=6×106)

图17、图18给出了高升力设计前后旋翼翼型在Ma=0.3,Re=6×106时的定常计算升力系数曲线和升阻极曲线对比。设计翼型相比基准OA212翼型,最大升力系数明显提升,在发生分离流动的大攻角附近减阻效果明显。

图17 12%厚度翼型高升力设计前后升力系数曲线对比(Ma=0.3,Re=6×106)

图18 12%厚度翼型高升力设计前后升阻极曲线对比(Ma=0.3,Re=6×106)

图19、图20分别给出了12%厚度翼型在0.3Ma、0.4Ma达到最大升力时的定常流场对比。可以看到,设计翼型通过抑制后缘分离流动,有效提高了最大升力系数。

图19 12%厚度翼型后缘分离流场对比(左:OA212,右:design12;α=15°,Ma=0.3,Re=6×106)

图20 12%厚度翼型后缘分离流场对比(左:OA212,右:design12;α=12°,Ma=0.4,Re=8×106)

表1列出了12%相对厚度旋翼翼型修型前后的气动性能对比,计算时保持相同的音速雷诺数(Re/Ma)。设计翼型的低马赫数最大升力系数明显提升,中等马赫数的阻力和零升阻力发散马赫数基本维持,力矩系数提高0.005。设计翼型在后部减小了翼型反弯度,因此在提高最大升力的同时,引起了低头力矩系数的增加。由此可见,在改善旋翼翼型后缘分离特性时,需要综合考虑对力矩特性的影响。

表1 12%相对厚度翼型设计前后气动性能对比

5.2 OA206翼型失速特性参数影响分析

薄翼型前缘发生分离后即表现出显著的非定常特性,常规手段难以有效控制分离后的流场。因此,结合失速前的流场特性进行设计,是提高翼型最大升力的有效手段。

薄翼型具有在前缘很短的一段距离即达到负压峰值的固有特性。因此,在翼型上表面前部适当调节曲率:一则降低前缘附近压力梯度,以维持失速攻角;二则增加压力分布曲线面积,以提高失速前升力系数。此外,增加翼型中后部弯度也可以提高最大升力,但会增加力矩系数,考虑到基准翼型的力矩系数较小,因此不采用该种途径。设计前后翼型外形对比如图21所示。8°攻角压力分布对比如图22所示。

图21 6%厚度翼型高升力设计前后外形对比

图22 6%厚度翼型高升力设计前后压力分布对比(α=8°,Ma=0.4,Re=6×106)

图23、图24给出了翼型在Ma=0.4,Re=6×106时的升力系数曲线和升阻极曲线的定常计算结果。翼型均在8°攻角后失速。与基准OA206翼型相比,设计翼型的最大升力系数稍有提升,失速前阻力明显减小。但由于上表面负压峰值增加,当马赫数增加时,上表面激波强度增强,导致高升力系数下的阻力增加,如图25所示。因此,针对薄翼型,以提升最大升力系数为目标进行前缘外形改进设计时,如采用改变前部曲率以增加前部压力曲线面积的方法,则需要兼顾中、高马赫数上表面激波强度。

表2列出了6%厚度翼型设计前后的气动性能对比,音速雷诺数取1.5×107。设计翼型在0.4Ma的最大升力系数提升1.4%,阻力发散马赫数和力矩特性基本维持,中等马赫数的阻力系数增加了2.5%。由结果可见,单纯依靠对薄翼型前缘局部外形作微调来提升最大升力系数的收益较小。

表2 6%相对厚度翼型设计前后气动性能对比

6 结论

本文通过对两个厚度的旋翼翼型开展数值模拟,分析了翼型的不同失速形态,并从翼型表面压力分布的角度解释了引起翼型失速现象的机理。然后根据不同厚度翼型的失速机理,开展了两个厚度旋翼翼型的失速特性参数影响研究。本文结论如下:

1) 厚翼型的失速现象通常是由后缘出现流动分离开始。失速初期表现为上表面后缘出现稳定的分离涡结构;随攻角增加,分离区域向翼型前缘方向扩展,一般翼型失速特性较为和缓。

2) 薄翼型的失速通常由前缘流动分离引起。翼型上表面分离涡周期性脱落,使得上表面阶段性地存在较大范围的分离区,导致翼型流场剧烈变化,表现出显著的非定常特性。

3) 对于发生后缘分离的厚度较大的旋翼翼型,可以通过提高翼型前缘曲率,同时抑制后缘流动分离的方式,达到提高最大升力的效果;在调整后缘流动时要兼顾力矩特性。

4) 受限于最大厚度和前缘半径,薄翼型的失速一般情况下皆由前缘失速主导。旋翼翼型设计时,首先需要避免前缘过早分离引发失速提前。在失速攻角不发生明显变动的前提下,可以通过适当增加压力曲线前部面积来提升翼型最大升力并维持较低力矩,但需注意兼顾高马赫数激波强度。