基于时间序列相似性的网络社区检测方法
王钧麟, 徐名海, 邹敬博, 李小龙
(南京邮电大学通信与信息工程学院, 南京 210003)
0 引 言
现实世界中存在着许多复杂系统,在这些系统中实体之间的确切关系是未知的或者不易观察到的,但仍然存在着非常明显的社区结构。 例如,在万维网中不同网站之间的关系是很难观察到的,但根据每个网络的主题不同可以发现万维网中具有明显的社区结构;在社会关系网络中不同的人之间可能由于没有交际导致其之间的关系不够完整,但根据不同的行为习惯、消费习惯也呈现了明显的社区结构;而在股票网络中,某些股票之间的关系是无法得知的,但根据不同的行业或者价格涨跌等,股票网络中也具有非常明显的社区结构。 在复杂网络中各个实体之间的确切关系是未知的、不完整的或不易观察到的,本文将这样的复杂网络称为隐边网络。
在隐边网络中,社区可以定义为具有相似的特定或者功能的个体的集合,在社区内部的每个个体之间的联系较为紧密,而位于不同社区间的每个个体之间的联系则较为稀疏。 认识和发现这些网络中的社区结构具有非常高的实用价值,可以帮助了解系统的内在运行机制,还可以为这个系统进行预测和控制提供较强的指导和帮助。 为了了解复杂系统中实体之间的关系,可以观察来自每个实体相互依赖的信号,如时间序列、事件序列等。 时间序列类型数据就是按照时间先后顺序排列各个观测记录的数据集,在现实世界很多领域中都广泛存在。
通过分析引起时间序列发生变化的具体内在原因,从而推断出个体之间的关系,例如贝叶斯模型、非负张量分解等方法。 不同于观察时间序列内在因素,本文选择观察每个个体时间序列的外在表现,通过分析每个个体之间时间序列的相似程度来表示其之间的关系,能够更加简单直观地描述复杂系统中每个个体之间的关系。
1 相关关键技术
1.1 序列相似性度量
复杂系统中每个实体之间的关系通过其时间序列的外在表现,即时间序列之间的相似程度能够更加简单直观地描述出来。 时间序列相似性度量有很多方法,如欧式距离、闵可夫斯基距离、皮尔逊相关系数、动态时间规整距离等。
欧式距离也称为欧几里得距离,是衡量时间序列之间距离最直接的方法,常常用来表示N维空间中两个不同对象之间的相似性。 由于欧式距离的计算简单高效,且可以体现时间序列中数值特征的绝对差异,因此常常用于时间序列相似性的度量。 但欧式距离只能计算相同长度的时间序列,不能实现数据异步匹配,且其度量质量容易受时间序列异常点、噪声的影响,不能够很好地满足不同时间序列距离计算的需求。 闵可夫斯基距离则是一种更为广泛的欧式距离,是欧式距离的推广。
皮尔逊相关系数用于度量两个变量X和Y之间的线性相关程度,两个定距的连续随机变量的皮尔逊相关系数等于两者之间的协方差与各自标准差乘积的商,数值在-1 到1 之间。 系数值越接近于0,则随机变量之间的相关程度就越低;系数值越接近于1,则变量之间呈现很强的相关关系。 系数的正负则表示了两者之间呈现的正负相关关系。 皮尔逊相关系数的计算,式(1):
其中,cov(X,Y) 为变量X和Y之间的协方差;σX,σY为变量X和变量Y的标准差;μX,μY为变量X和变量Y的均值。
动态时间规整距离是一种衡量两个长度不同的时间序列之间相似度的方法,通过把时间序列延伸和缩短,使得不在同一时间点上对应的波峰或波谷也能够被对齐,忽略不同时间序列之间在时间上的错位与滞后的问题,具有较好的鲁棒性。 本质上是通过最小化时间序列间的累计距离,以动态规划的方式来寻找两个时间序列之间最优的对齐路径。 对于两个长度不同的序列X=(x1,x2,…,xm) 和Y=(y1,y2,…,yn) ,序列之间点的距离定义为d(i,j) ,距离公式可以任意选定,可以简单地选择为欧氏距离;按照顺序计算系列X中的每个点与序列Y中的每个点之间的距离,生成对齐矩阵。 为了获得这个对齐矩阵,首先需要得到一个序列距离矩阵D,其中行对应X序列,列对应Y序列,矩阵元素D(i,j) 表示点xi与点yj之间的动态时间规整距离d(i,j) ,表示从原点 (0,0) 出发到达点(i,j) 需要累计的最小距离。D(i,j) 的计算,式(2):
对齐矩阵中的D(m,n) 的值即为两个序列之间动态时间规整距离的结果。
1.2 复杂网络社区检测
自2002 年Girvan 和Newman 基于边介数提出GN(Girvan-Newman)算法进行社区检测以来,国际上掀起了一股社团检测的研究热潮。 社区检测早期的研究工作大部分都是围绕非重叠社区检测展开的,非重叠社区检测算法识别出的社区之间互不重叠,每个节点仅属于一个社区,包括基于图分割的社区检测算法和基于层次聚类的社区检测算法等。
Kernighan-Lin 算法是典型的基于图分割的社区检测算法。 首先将网络一分为二,形成两个大小已知的集合,定义一个增益函数Q,表示集合中的内部边连接数减去两个集合之间的边连接数,目标是通过改变节点间的连接使得增益函数最大化,最终获得划分结果。 该算法开始阶段需要知道网络的规模以及划分个数,不适用于现实网络。
基于层次聚类的社区检测算法是通过衡量网络中节点之间的相似度来检测网络中的社区,分为凝聚算法和分裂算法两种。 凝聚算法的主要思想是将相似的节点不停地进行合并,直到合并为一个社区为止;而分裂算法则是将网络中节点不断进行划分,直到每个节点代表一个社区。 GN 算法、Newman 快速算法和Louvain 算法等都是基于层次聚类的方法。 GN 算法属于基于分裂的层次聚类算法,其主要思想:首先对网络中每条边的介数值进行计算,然后将介数值进行排序,每次选出其中的最大值,将该最大值所对应的连边从网络中移除,从而将网络划分为多个社区。 边的介数值等于网络的全部最短路径中通过这条边的路径的个数与全部最短路径个数的比值。 为了衡量网络划分的质量,又引入了模块度函数的概念,当模块度函数达到最大值时认为此时网络划分得最好。 而Louvain 算法是基于模块度最优化的启发式算法,该算法主要包含两个阶段,第一个阶段不断地遍历网络中的节点,尝试将单个节点加入能使模块度提升最大的社区中,直到所有节点都不再变化;第二个阶段将第一阶段形成的一个个小的社区归并为一个超节点来重新构建网络,并且计算其连边权重。
2 现实应用场景和网络社区检测方法
2.1 现实应用场景
现实生活中存在着很多个体具有时间序列数据的复杂系统,利用这些时间序列数据进行网络社区检测的应用场景如图1 所示。 图1 中左半部分可以表示为复杂系统中的各个个体,各个个体之间的确切联系是未知的、不完整的或者不易观察到的,中间部分则是每个个体所对应的时间序列数据或事件序列数据,右半部分是根据中间部分的数据将左半部分的个体划分为具有不同特征的社区结构。 例如,在一个道路交通系统中,左半部分的个体可以表示为每个不同的地点,根据每个地点地域是否相连等会存在一些联系,但总体上联系是不易观察的,而每个地点具有交通客流量等时间序列的数据,可以表示为中间部分的数据;在一个社会关系系统中,左半部分的每个个体可以表示为不同的人,每个个体之间的确切关系可能不容易被观察到,而中间部分则是每个人所对应的消费记录、行为习惯或做某件事的频率的一些时间或者事件序列的数据。 本文要在系统中个体之间的确切关系是未知或者不易观察时,利用每个个体所对应的时间或者事件序列数据检测出这些系统中具有不同特征的社区结构。
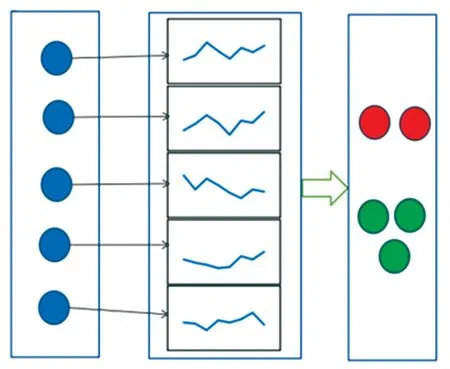
图1 应用场景Fig. 1 Application scenario
2.2 基于时间序列相似性的网络社区检测方法
为了简化复杂网络的模型,本文假设在复杂系统中个体之间不存在任何关系和联系,每个个体之间的联系仅由其时间序列的相似性来决定。 首先,获取到复杂系统中每个个体所对应的时间序列数据;其次,对每一对时间序列之间的相似性进行计算,得到每个个体之间的关系,从而可以构建出一个全连接的复杂网络。
全连接的复杂网络中包含了很多相似性较低的冗余信息,对整个系统和网络的分析并没有太大的价值。 因此,本文对网络中节点之间的连边进行筛选,去除网络中一些不重要的边,仅保留真正能反映节点之间关系的边,使得对网络的理解和分析更加准确,本文选择阈值法来简化网络。 阈值法是通过确定一个特定的阈值,将距离小于选定阈值的连边从网络中过滤掉。 一般情况下,阈值的确定方式有两种:一是通过观察节点之间相似关系的分布给定相应的阈值;二是选取一个仅保留网络中相似关系最高的前K%的连边的阈值。 将相似性网络简化后,利用复杂网络的社区检测算法检测复杂系统中的社区结构,并对其检测结果进行理解和分析。
3 上证股票网络社区实证分析
3.1 实验数据获取与预处理
上证180 指数成分股中的控股公司均是从金融、制造业、房地产等行业中挑选出的大型公司,这180 只股票的行业代表性较强、规模较大、流通性较好,能够比较客观且全面地描述上海股票市场的整体运行状况和不同股票之间的关系。 因此,本文选取上证180 指数的所有成份股票作为研究对象,样本数据为2020 年1 月1 日至2022 年3 月31 日每只股票在每个交易日的收盘价格,长期的时间跨度能够保证样本数据的有效性。
上证180 指数成分股票遵循稳定性与动态性相结合的原则,每隔一段时间就会对其中的股票进行一次调整。 为了确保实验结果的有效性和可靠性,对于不能获取这段时间内全部收盘数据的股票进行删除,最终选取上证180 指数成分股中的162 只股票作为研究对象。
3.2 网络构建与实验结果分析
3.2.1 网络的构建
为了更准确地描述股票价格的波动性,本文对获取得到的股票收盘价时间序列进行归一化处理,得到每只股票的对数收益率时间序列作为输入,对数收益率的计算,式(3):
其中,Pi(τ) 表示时间点τ的股票收盘价,Δt为计算对数收益率的时间间隔,通常取1 个交易日作为时间间隔。
得到每只股票对数收益率时间序列后,可以根据皮尔逊相关系数计算任意两只股票i和j之间的相关系数,从而得到一个系数对称矩阵C来描述这个全连接的股票网络,系数矩阵C,式(4):
其中,ρi,j表示股票i和股票j对数收益率序列的皮尔逊相关系数。
本文选用阈值法简化全连接的股票网络,需要对各个股票之间的相关系数进行统计分析,确定相应的阈值。 各股票间的对数收益率相关系数的概率分布曲线如图2 所示,基本服从正态分布,只有很少数股票之间呈现负相关关系,绝大多数股票之间的相关系数都在0.2 ~0.4 之内,有极少数股票之间相关系数在0.8 以上。 这表明在股票市场中,绝大多数个股之间的相似关系并不显著,仅有极少量的个股之间呈现出非常显著的关联关系。
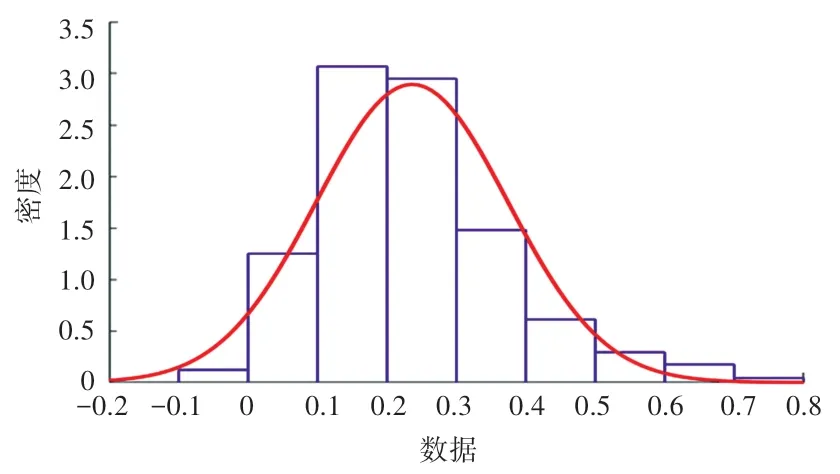
图2 股票间相关系数统计分布Fig. 2 Statistics of correlation coefficient between stocks
利用阈值法构建网络,选取不同的阈值得到的网络结构也是不同的。 若选择的阈值较低,网络中会保留较多次要的连边,导致网络过于复杂,难以提取其中的重要信息;反之,若选择的阈值较高,虽然可以过滤掉绝大数冗余的信息,但此时网络中连边的数量过少,会使得一些有用的关联信息丢失。 因此,本文一步一步提高阈值,得到一个稳定的网络结构,从而确定一个合适的阈值。 选择不同的阈值过滤后网络中的有效连边占初始网络的比重如图3 所示。
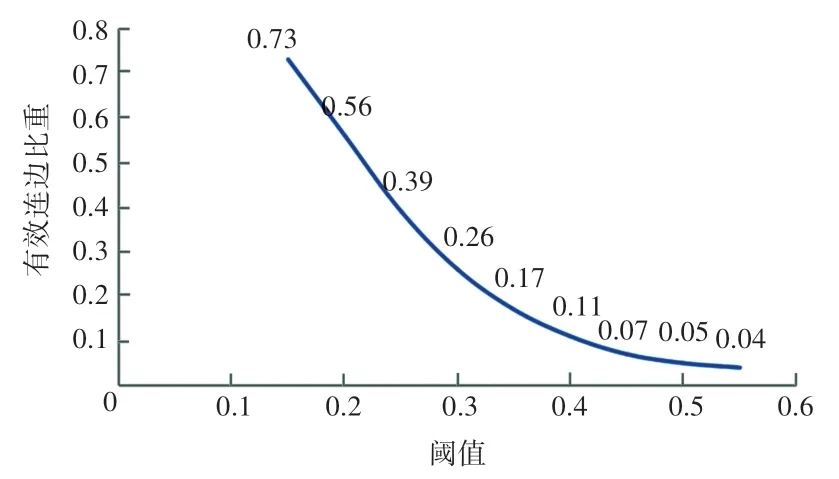
图3 不同阈值时网络中有效连边所占比重Fig. 3 The proportion of effective edge connection in the network at different thresholds
观察选取不同阈值过滤后得到的网络,将阈值设定为0.4,经过过滤后的网络连通图如图4 所示,此时的网络被简化,保留了重要连边信息,同时网络中也会出现一些孤立节点。

图4 简化后的股票网络连通图Fig. 4 Simplified connected graph of stock network
3.2.2 网络结构特征分析
3.2.2.1 度和度分布
一个节点的度值越大,说明网络中有越多的节点与这个节点之间存在直接的连边,即该节点在网络中的影响力越大。 在上证180 指数成分股票关联网络中,节点的度分布如图5 所示。 为了更加直观地判断其度分布是否符合幂律分布,需要对累积度分布曲线进行拟合,得到股票关联网络的双对数的累积度分布曲线如图6 所示,该累计度分布曲线具有非常明显的幂律特性,说明该股票关联网络具有无标度特性。
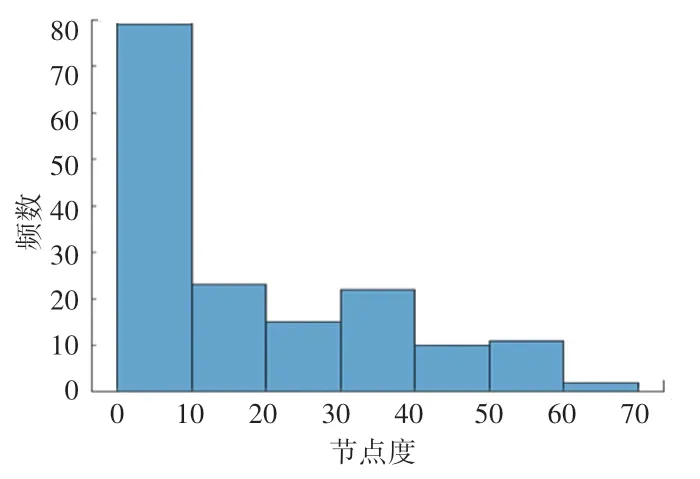
图5 上证180 指数成分股票网络节点度分布图Fig. 5 Node degree distribution of Shanghai 180 index component stock network
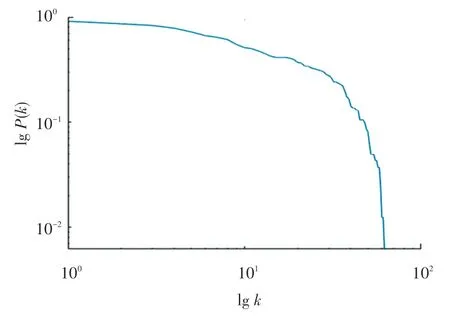
图6 上证180 指数成分股票网络双对数累积度分布图Fig. 6 Distribution of double logarithmic cumulative degree of the stock network of the Shanghai 180 index components
3.2.2.2 平均路径长度和聚类系数
将上证180 指数成分股票关联网络与模拟生成相同规模的随机网络的统计指标进行比较,结果见表1。 可以发现,上证180 指数成分股票关联网络具有小世界性。 因为该网络的平均路径长度较小,约等于随机网络的平均路径长度,即在股票关联网络中的所有股票都能够通过较短的路径获得关联;并且该网络的平均聚类系数远大于随机网络的平均聚类系数,说明网络中某只股票的价格发生变化时,其周围的股票更容易受到影响,且受到影响的程度通常都比较大。
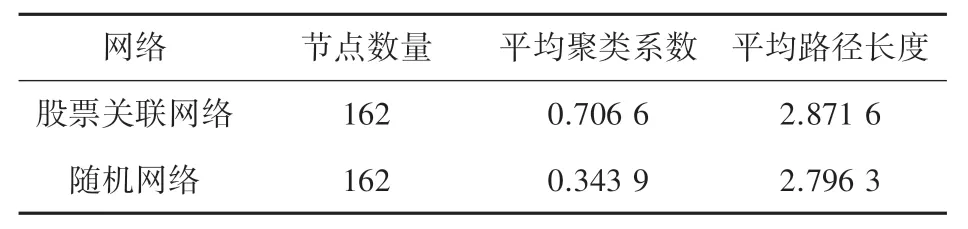
表1 上证180 指数成分股票网络与随机网络统计指标Tab. 1 Shanghai 180 index component stock network and random network statistical indicators
3.2.3 网络社区结构分析
本文运用Louvain 算法对上证180 指数成分股票关联网络进行社区划分,整个股票网络共被划分为22 个社区,绝大部分股票被划分在其中6 个社区中。 由于通过阈值法对连边进行过滤时会产生一些孤立的节点,所以在社区划分中通常都分别属于不同的社区。 社区划分后网络中主要的社区中所包含的股票数量见表2,整个网络社区划分结果如图7所示。

表2 上证180 指数成分股票网络主要社区内部股票数量Tab. 2 Number of stocks within the main communities of the Shanghai 180 index stock network
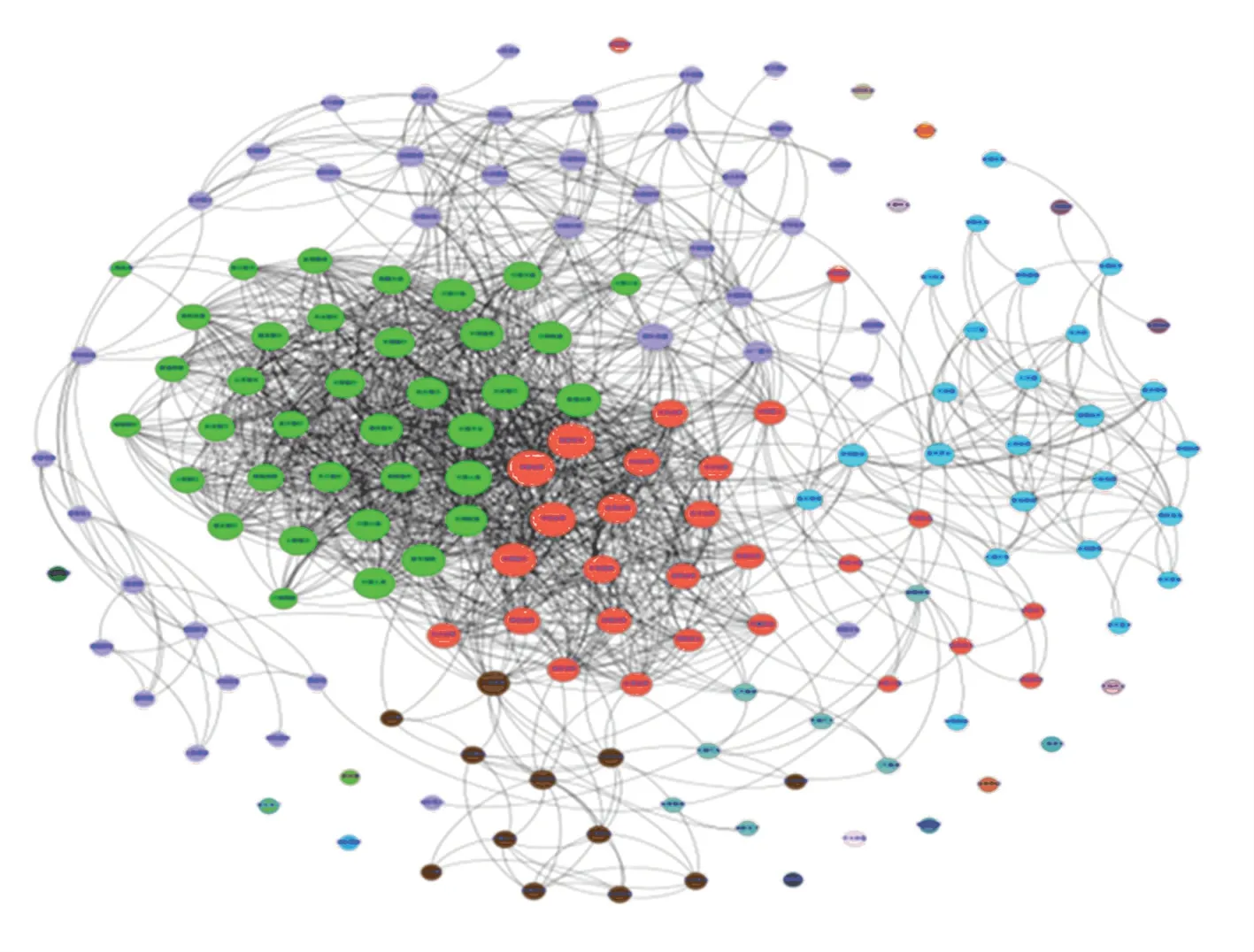
图7 上证180 指数成分股票网络社区划分结果图Fig. 7 Result chart of Shanghai 180 index component stock network community division
从图7 中可以看出,利用Louvain 算法对股票关联网络进行社区划分的结果较好,社区的结构也较清晰。 为了进一步挖掘网络中社区内股票的相关信息,本文统计了其中几个主要的社区内部所有的股票信息,这些社区的股票构成见表3。 社区1 中的股票成员大部分都是能源以及基础建设行业板块的股票;在社区2 和社区3 中的股票成员分别属于金融业中两个不同的子行业,银行和证券;在社区4 中都是一些来自制造业板块的股票;而在社区5 中的股票成员则是属于电子信息板块。 通过社区划分结构可见,大多数股票社区内部股票都呈现出具有同行业或者相关行业的特征,即隶属于同一行业板块的股票更加倾向于被划分到同一个社区当中。 这也是符合常理的,因为属于一个行业板块的股票所面临的市场环境和外部环境等因素都是类似的,受到经济、供求关系以及政策的影响也是较为相同的,使得在同一个行业板块的股票之间具有更加紧密的联系,所以更倾向于划分到同一个社区。 另外,本文还对每个社区中具有更高度值的节点进行分析,例如中国石化、浦发银行、国泰君安属于网络中的关键节点,对整个社区乃至整个股票网络的波动都会产生比较重大的影响。
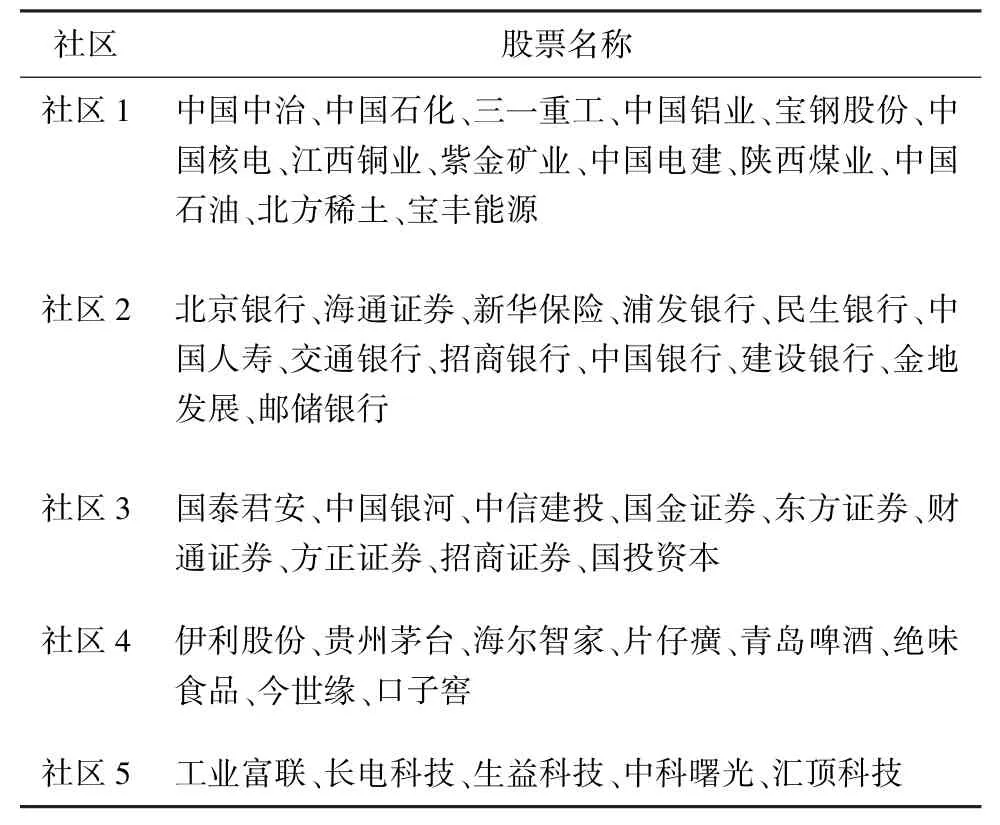
表3 不同社区内的股票构成Tab. 3 Share composition in different communities
通过复杂网络对股票网络进行社区划分是从定量的角度来衡量各个股票之间价格波动的相似性,比单纯通过行业板块进行区分更加精准。 在进行股票投资组合的时候,可以根据划分的不同社区进行分散投资从而降低投资风险;而在不同社区进行投资时,则可以密切关注这些具有较高度值的股票,帮助投资者选取不同的股票进行投资。
4 结束语
本文基于时间序列的相似性以及复杂网络理论对网络中最重要的特性——社区结构进行了相应的分析,并利用上证180 指数成分股票的时间序列数据对其网络进行了社区结构的分析,表明利用时间序列相似性对现实经验世界中的复杂网络的社区结构进行分析和解释其内在运行机制是有效可行的。但本文忽略了复杂系统中每个个体之间原本存在着一定的联系,仅仅利用每个个体时间序列之间的相似性表示每个个体之间的关系,没有非常准确地描述现实场景。 未来的工作应该考虑保留复杂系统中个体之间原本的联系,再结合时间序列之间的相似性,考虑复杂系统每个个体之间不同类型的关系的结合并分析其对复杂系统的社区结构的影响,从而能够更精准地预测和控制这些复杂系统。

