基于麻雀算法优化的神经网络推荐算法研究

黄承宁， 孙自梅， 张 斌， 朱玉全

（1 南京工业大学浦江学院， 南京 211222； 2 江苏大学计算机科学与通信工程学院， 江苏 镇江 212013）

0 引 言

在智慧校园建设中，信息过载现象越来越严重，而学生培养方案存在过于单一规范问题，无法反映不同学生擅长的领域，更无法针对性推荐引导自主学习，无法充分发挥不同学生真正的学习能力。 基于用户画像的自主学习推荐，是根据学生人才培养方案课程学习情况数据分析，对学生学情进行画像描述与分析，进而实施个性化推荐，提供适合学生的学习领域和职业课程知识。 基于画像，可以根据学生的特点，深入了解适合学生的特定领域，让学生学习真正有用的技能，为学生将来进入社会打下坚实的基础。

用户画像是通过分析用户行为特征、消费习惯和其他有关用户行为的信息而构建的一种用户特征［1］。 根据用户的特点，公司对其进行精准营销，为改善用户体验、吸引用户注意力奠定基础。 例如：淘宝和抖音等互联网公司，通过分析购物记录和浏览用户数据，为每个用户构建一幅画像。 当用户再次登录时，其会根据用户画像推荐专属商品，以方便用户购物。 在高校，智能图书馆可以根据用户画像为学生提供准确的知识服务，并为研究团队提供学科知识服务。 用户画像的构建方法包括：基于用户兴趣偏好、用户行为、动机、个性特征和角色情绪等等。

推荐算法是推荐系统的重要组成部分，该算法通过收集用户特征、行为和推荐元素的特征，计算出最接近用户偏好的元素。 推荐算法分为3 类：基于内容的推荐（Content-Based， CB）、基于协同过滤的推荐（Collaborative Filtering， CF） 和混合推荐（Hybrid Recommendation）算法［2］。 其中，基于内容的推荐算法是通过用户特点，推荐其喜欢的特征项目；基于协作过滤的推荐算法是就目前最有效的推荐算法，其假设两个用户有相似的兴趣，那么当前用户很可能会喜欢另一个用户喜欢的项目；混合推荐算法结合了两种或两种以上的算法，最大限度地发挥每种算法的优势，并使最终的推荐结果更接近用户的偏好。

目前，推荐系统通常根据用户画像特征，推荐与用户偏好标签匹配的商品，但此方式存在信息茧房问题，即不能推荐提供用户更多弱关联信息。 如：用户标签显示不喜欢或者弱需要的，或者推荐对象的某些属性被忽略等问题。 造成这种情况的主要原因，是获得用户兴趣和喜好的方法以及提取特征的方法不是非常适用，该系统难以获取用户的兴趣和偏好，无法匹配推荐对象的内容特点，更难以获得用户满意的推荐结果［3-4］。 因此有必要引入更准确、更合适的用户和对象特征。 模型持续改进的前提和关键，是找到更多的应用场景进行测试和修正；同时应考虑到多变的环境和利用用户认知能力，避免技术过程崩溃的可能性。 因此，目前在理论和技术上存在很大差距，主要表现在缺乏多种应用场景，导致模型技术及其转化应用的能力缺乏持续改进。

深度学习方法最常用的分类器为卷积神经网络，卷积神经网络是含有卷积层、池化层等多个层次的深度神经网络模型，在数据训练时很容易产生过拟合现象，同样存在致使准确率降低的问题［5］。 而麻雀搜索算法的搜索过程中引入随机性，其并不是一种确定性算法（Deterministic approaches），所以其很好的解决了确定性算法在复杂问题上陷入局部最优的缺陷，所以麻雀算法在求解全局优化问题的最优解方面具有重要的现实意义。 但是，在实际研究中发现，麻雀搜索算法在处理复杂问题上仍然容易处于局部最优，但全局搜索能力稍有改善。

综上所述，本文基于Anaconda 环境，使用Python 和PyTorch 框架，在GPU 处理支持下，对模型进行加速训练验证。 首先对数据集进行了训练分割，然后研究了神经网络模型和最新的麻雀算法，并进行基于麻雀算法改进DNN 分类推荐算法的设计，最后开展模型实验以及优化，寻找出麻雀算法的适用范围，并对深度神经网络模型的推荐性能进行优化分析，最终实现基于麻雀算法的神经网络模型的推荐性能研究优化提升。

1 相关研究工作

1.1 神经网络与麻雀算法

深度神经网络，又称多层感知机，是以人类神经元之间的协作学习为模型的复杂网络结构［6］。 网络分为3 层：输入层、隐藏层和输出层。 输入层将数据传递给模型，让模型进行研究；隐藏层为中间表示层；输出层负责输出模型学习结果。 网络结构示意如图1 所示。

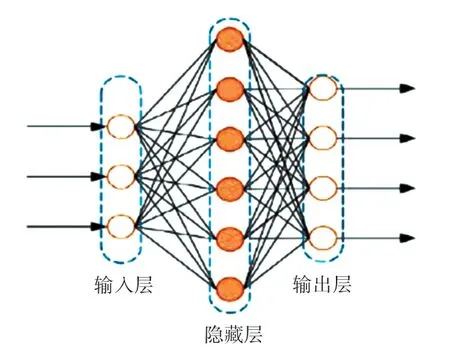
图1 深度神经网络结构示意图Fig. 1 Schematic diagram of deep neural network structure

群优化算法根据模仿机制的不同，可分为生物现象模仿和确定性物理定律设计的启发式模拟。 常见的生物现象的模仿算法有：模拟人类社会进化的遗传算法（Genetic Algorithm）、热带雨林生长的雨林算法（Rain Forest Algorithm，RFA）、蚂蚁觅食行为的蚁群算法（Ant Colony Optimization，ACO）、鸟群觅食行为的粒子群算法（Particle Swarm Optimization，PSO）、蜜蜂觅食行为的蜂群算法（Bee Colony Algorithm， BCA）、细菌觅食优化算法（Bacterial Foraging Optimization， BFO）、麻雀觅食分层思想的麻雀算法（Sparrow Search Algorithm，SSA）等［7］。 其中，麻雀搜索算法的搜索过程中引入随机性，其并不是一种确定性算法（Deterministic approaches），因此在求解全局优化问题的最优解具有重要的现实意义。 但是在实际研究中发现，麻雀搜索算法在处理复杂问题上仍然容易处于局部最优，但全局搜索能力稍有改善。

1.2 神经网络模型设计

深度神经网络的显著特点是其神经元的多层次结构，与其它神经网络一样，也有输入层和输出层［8］。 在输入和输出之间，可以任意地设置多个隐藏层，而隐藏层的数量取决于所要解决问题的大小。深度神经网络是完全连接的，这和其它的神经网络有很大的区别。 如图2 所示，在每个神经元的输入信号中，首先由神经网络进行线性转换，然后通过激活函数进行非线性转换，最后经过多层隐藏层之后进入输出层输出。 若要解决分类问题，则要将输出归一化或者经过其他形式的激活函数进一步处理。

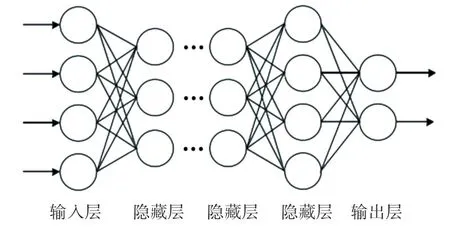
图2 深度神经网络结构图Fig. 2 Structure of deep neural network

经过上述分析，本文模拟的函数本质上属于分类问题，基于对标签的观察，需要对输出进行归一化。 通过神经网络将输入的数据输入到神经网络中，然后通过与标签的比较，来确定适合的梯度下降算法。 本文系统采用了5 层神经网络结构，其中包括1 个输入层、1 个输出层和3 个隐藏层。

1.2.1 激活函数的选择

激活函数又称传递函数，可以把数据训练过程转换为非线性运算，来更好的求解复杂的问题［9］。激活函数具有非线性、单调性、可微性的特点。 因为对激活函数的优化有梯度性，所以可微是必不可少的一个特性。 正是由于激活函数增加神经网络模型的非线性，同时使得梯度优化更为稳定、模型训练更为高效，因此选择合适的激活函数可以提升神经网络性能。 常见的几种激活函数如下：

1.2.1.1 Sigmoid 函数［10］

输入的数据通过Sigmoid 功能进行处理，则输出的数值在0～1 之间。 若输入的数据非常大，则输出为0；如果输入数据的绝对数值很小，输出就是1。

Sigmoid 函数公式如式（1），函数图像如图3所示。

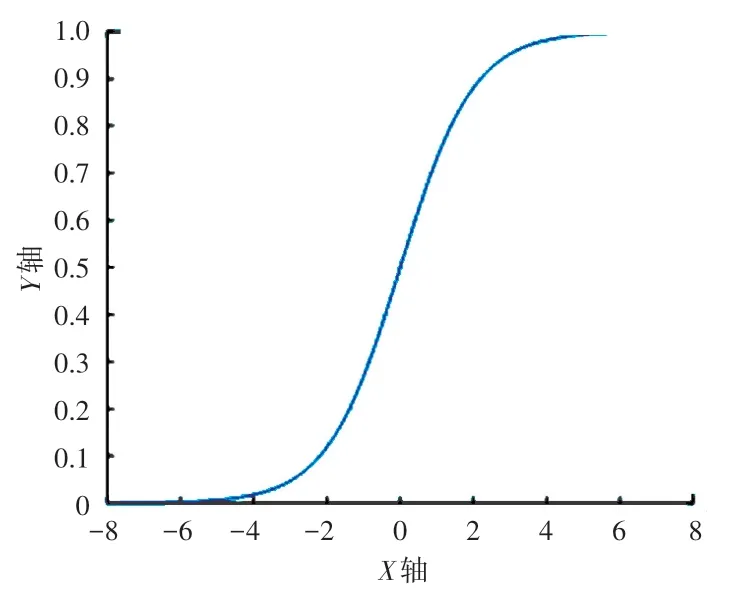
图3 Sigmoid 函数图像Fig. 3 Sigmoid function image

一般情况下，Sigmoid 激活函数能够很好的应用于二分类问题，通过计算输出的概率进行结果的判决。 但Sigmoid 函数也存在一定的局限性，当需要大量计算时，会影响函数的收敛速率，导致训练速度下降；当输入值过大和过小时，梯度会向0 逼近，而数据反向传输时，容易导致模型梯度的消失。

1.2.1.2 Tanh 函数［11］

Tanh 函数是一种基于Sigmoid 函数的转换，公式如式（2），函数图像如图4 所示。

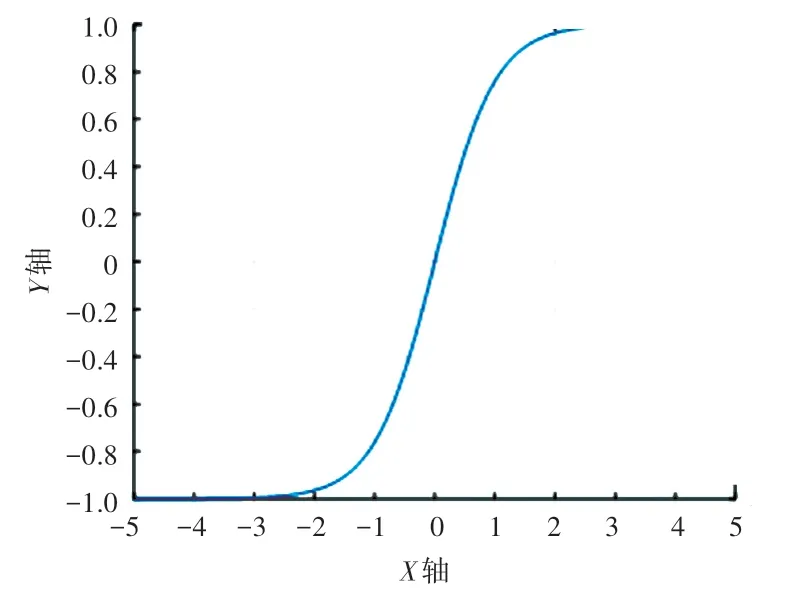
图4 Tanh 函数图像Fig. 4 Tanh function image

同Sigmoid 函数相比，Tanh 函数输出值映射范围在-1～1 之间，函数图像如图4 所示。 由于Tanh函数输出均值为0，因此网络训练的收敛性更强。但是，如果输入值变大或变小，梯度也会随之消失。

1.2.1.3 ReLU 函数［12］

如图5 所示ReLU 激活函数的映射规则为：当输入值为负数时，映射结果为0，其余数值不进行映射。 由于ReLU 函数在x ＞0 的情况下梯度不会发生变化，因此很好的解决了Sigmoid 与Tanh 函数存在的局限性问题。 该方法不仅计算方法简单，而且收敛速度较快。 但此函数也存在因为梯度过高而被置0，导致神经元可能再也无法被数据激活。

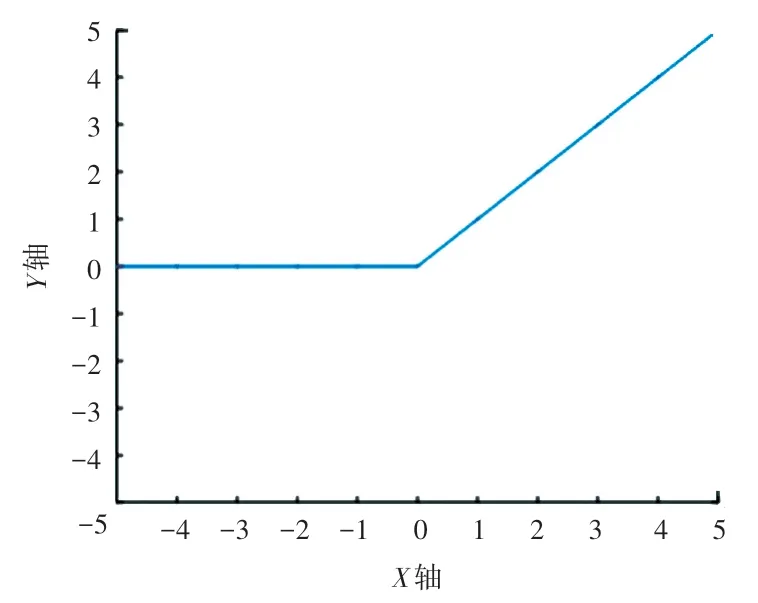
图5 ReLU 函数图像Fig. 5 ReLU function image

1.2.1.4 ReLU6 函数［13］

由于ReLU 函数的梯度是1，当输入数据是一个很大值时，对应的输出值受其影响也会很大，导致网络不稳定。 为了避免这一情况，可通过使用ReLU6函数来消除该函数的线性增长。 ReLU6 表达式如式（4），ReLU6 函数与导函数如图6 所示。

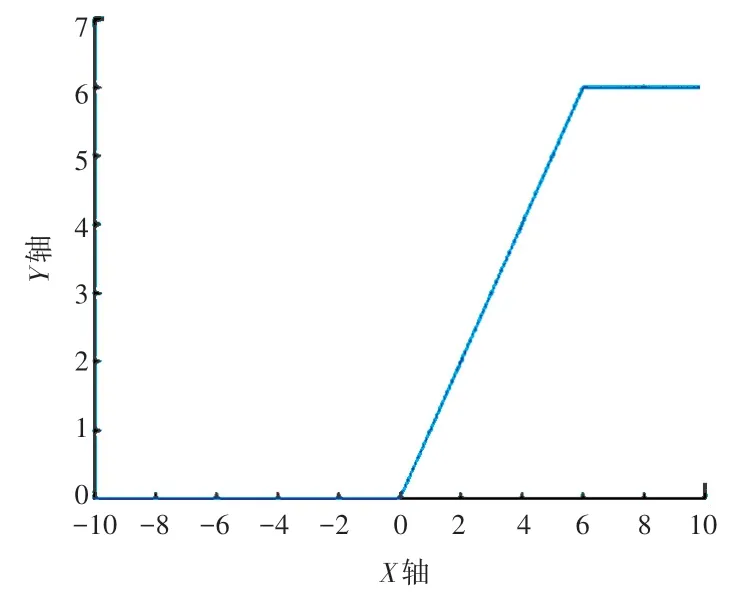
图6 ReLU6 函数图像Fig. 6 ReLU6 function image

本文针对激活函数的选择实验中，采用控制变量对比法，选择最佳激活函数，参数设定见表1。 实验针对上述4 种激活函数进行，比较结果如图7 所示。

表1 激活函数对比实验参数设定Tab. 1 Parameter setting of activation function comparison

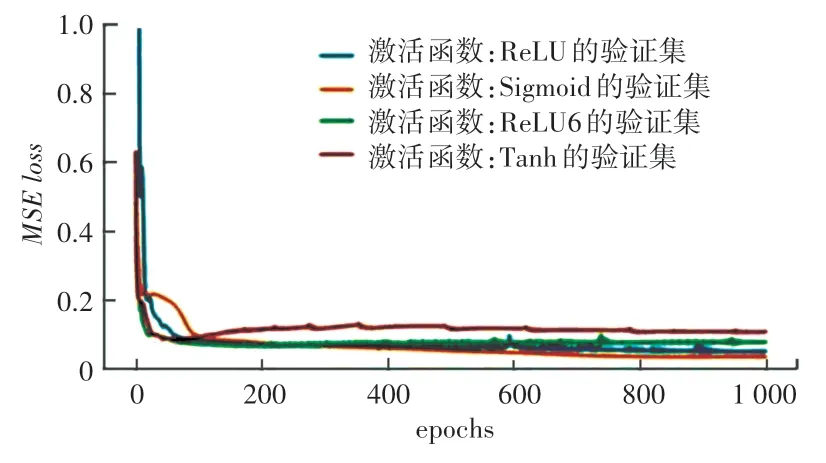
图7 4 种激活函数验证数据集结果比对实验Fig. 7 Comparison experiment of four activation function validation datasets

由图7 可见，Sigmoid 激活函数在训练集趋于收敛的情况下，验证集并未发散，未出现过拟合情况，因此本文选择Sigmoid 激活函数作为DNN 神经元的激活函数。

1.2.2 梯度下降优化器的选择［14］

梯度下降是一种寻找函数极小值的优化方法，在模型训练中学习率控制着每次更新参数的幅度，是比较重要的模型超参，过高或过低的学习率都可能对模型结果带来不良影响。 为了使学习率对模型训练过程起到良性促进作用，需要不断调整学习率，根据本文模型对以下两种梯度优化算法进行比对选择。

1.2.2.1 Adam-自适应矩估计［15］

Adam 首先计算梯度一阶矩E（x） 和二阶矩E（x2） 估计，并据此为不同参数设置独立的自适应学习率。 传统的随机梯度下降中，是按照固定学习率更新所有参数权重，而在Adam 策略中，其为每一个参数保留一个学习率，以提升在稀疏梯度上的性能。 当初始化的梯度和衰减率都很低时，Adam 使用梯度的一阶矩估计和二阶矩估计来修正梯度，提高梯度在参数空间内的稳定性，如下所示：

所以Adam 梯度下降算法的参数更新公式为

1.2.2.2 RMSprop［16］

为了解决Adagrad 学习率下降太快的问题，在文献［21］中作者采用Geoff Hinton 提出了RMSprop梯度下降法，参数更新公式如下：

由此可见，RMSprop 梯度下降法是将学习率分解成平方梯度指数衰减的平均。

本文采用控制变量对比法，选择最佳梯度下降优化器，参数见表2。 优化器选择中，针对Adam 和RMSprop 梯度下降优化器进行比较，学习率设定为0.001，并且在此参数下进行了对比实验。

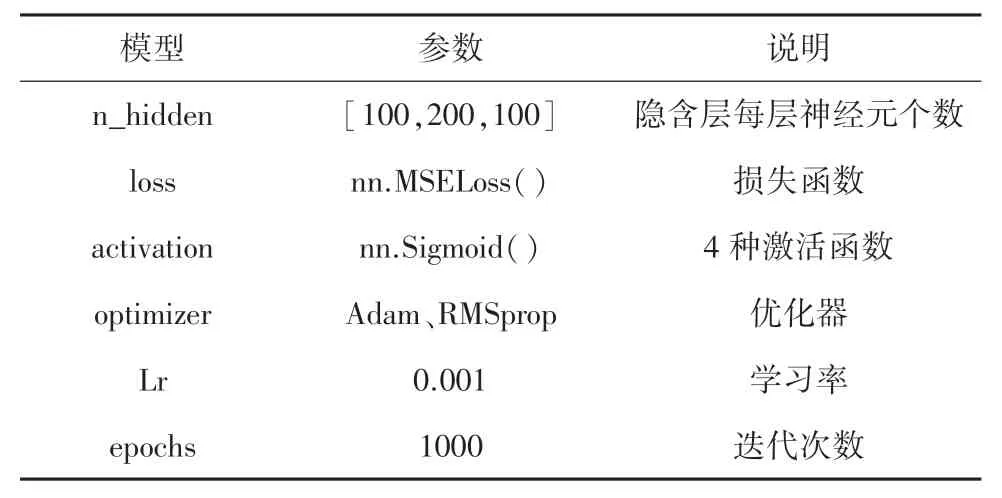
表2 梯度下降优化器对比的参数设定Tab. 2 Parameter settings for gradient descent optimizer comparison

在表2 参数下，对DNN 模型进行训练，图8 记录了模型训练过程中训练集的MSE损失函数值。可以清晰发现，当梯度下降优化器为Adam 时，DNN模型训练集的损失值下降速度最快，且收敛平稳；而RMSprop 前期损失函数值下降快，但却不收敛，迭代后期不平稳。

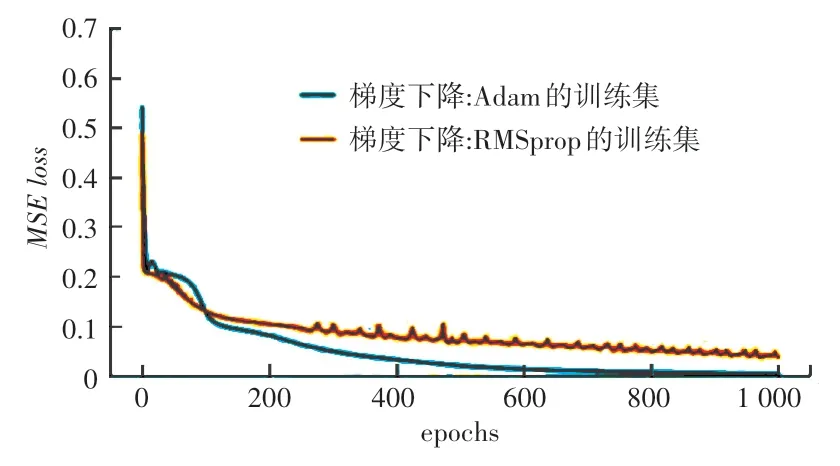
图8 两种梯度下降训练集结果对比Fig. 8 Comparison experiment of two gradient descent training sets

在设置优化参数下，对DNN 模型进行训练，图9 记录了模型训练过程中验证集的MSE损失函数值。 由图可见，当梯度下降优化器为Adam 时，DNN模型验证集的损失值下降速度最快，且收敛平稳；而RMSprop 前期损失函数值下降快、不收敛，迭代后期不平稳。

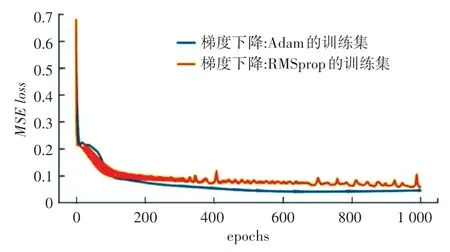
图9 两种梯度下降验证集结果对比Fig. 9 Comparison experiment of results of two gradient descent verification sets

通过对以上实验结果分析，故选择Adam 梯度下降优化器作为本文中DNN 网络的优化器。 对此，单独对Adam 进行训练集与验证集的损失函数值随迭代变化实验。 Adam 梯度下降优化器下的训练集和验证集的实验结果如图10 所示。

1.3 麻雀算法设计

麻雀算法的搜索机制，是在一次搜索结束后，都会更新麻雀所在位置；而在每一次更新位置之前，先根据麻雀当前觅食处的食物总量进行分配身份，食物总量多的分配成发现者，剩余的分配成跟随者［17-19］。 在发现者与跟随者麻雀搜索完毕后，通过随机抽取的方式，分配警惕者身份，更新警惕者位置。

基于此，本文提出了一种改进的麻雀搜索算法，具体改进如下：

（1）融合鸟群搜索算法中发现者位置更新策略，在寻优过程中代入上一代全局最优解，提升搜索充分性；

（2）在跟随公式中增加自适应因子，提高跟随者麻雀搜索范围，提升寻优能力。

发现者麻雀位置更新见式（10），虽然ST固定警惕阈值∈［0.5，1］，但一般取值0.8。

由式（10）中判断条件可知，R2＜ST概率大于R2≥ST，发现者麻雀群落中的大部分麻雀位置更新机制是基于在原有位置基础上再做跳跃。

跟随者麻雀位置更新见式（11），从公式的判断条件可知，跟随者麻雀中满足i ＞n／2 条件的位置属于较差位置，这些麻雀可称作乞丐麻雀（食物少的麻雀）。 乞丐麻雀的更新位置机制是每一维度在原点左右跳跃，试图找到食物更好的地方。 非乞丐麻雀在更新位置时，每一维度都往发现者麻雀中的最佳位置靠近。

警惕者位置更新见式（12），更新原则是发现者麻雀与跟随者麻雀更新完毕后，对更新后的麻雀群落随机抽取麻雀的方式，分配警惕者麻雀群落。

由公式（11）中判断条件可知，满足条件的警惕者麻雀数量为极少部分（几乎仅为一只）。 这只幸运的麻雀会逃离自身位置，更新的位置是在基于自身原有位置上位移，位移距离由自身距离和最差距离的差值与自身食物和最差食物的差的比值。 剩余麻雀几乎占据所有警惕者麻雀的群落，在更新位置上，朝着最佳位置大幅度位移。

1.4 基于麻雀算法改进DNN 分类推荐算法设计

1.4.1 深度神经网络模型推荐性能分析

1.4.1.1 交叉熵损失函数［20］

由于模型预测值和真实值之间存在差距，为此引入交叉熵进行描述，具体表达如式（13）所示：

式中DL（p ｜｜q） 为相对熵，代表了p与q存在的差异大小。 相对熵越大代表两者之间的差异性越大；反之，相对熵越小说明两者之间的差异性越小；而当相对熵等于0 时，意味着两者之间的概率分布是一致的。 在进行分类问题的处理时，该函数的表达如式（14）所示。

式中＝（0，0，…，0，1，0，…） 为＝m的独热编码，代表第i个样本的数据输出。 其中，第m维为1，而在该误差评判标准下，标签归属于第m类别； ¯yi为网络输出数据；N为样本的数量。

由于yi概率分布是确定的，即熵的值确定，则不会对网络的优化训练造成影响，若样本数据的类别是m，则样本中类别数量为C，则损失函数变换如式（15）所示：

若神经网络选用Sigmoid 作为激活函数，当网络梯度下降时，交叉熵能够利用误差控制网络学习速率，以解决使用均方误差损失函数时学习速率下降的问题。

1.4.1.2 均方误差损失函数［21］

在解决回归问题时，均方误差代表了神经网络的预测输出与真实标签之间误差的平方，函数公式如式（16）所示：

式中：N代表训练样本中的数据量，yi∈R代表第i个样本的真实值，¯yi代表神经网络的预测输出。 其中，预测输出与标签的数据格式保持一致，即标签为具体数值时，相应的预测结果也是特定的数值。

本文研究表明，所提出的神经网络所需的捕获算法都是一种回归问题，故选用均方误差作为损失函数。

1.4.2 基于麻雀算法改进的DNN 分类推荐算法流程

基于麻雀算法改进DNN 分类推荐算法的流程如图11 所示。 首先设置迭代次数，初始化麻雀算法中每一个个体的适应度值，进行搜索迭代；将每一只麻雀位置的四维数据传入DNN 模型进行训练，训练完毕后将测试集放入模型进行预测，并得出均方误差MSE；将MSE作为每一只麻雀的适应度值，发现者麻雀、跟随者麻雀、警戒者麻雀位置更新完毕后，迭代次数加1，若未达到迭代次数，则进行新一轮的搜索。

2 模型实验与优化

2.1 数据集

本文提出的基于麻雀算法改进的模型推荐算法涉及数据集主要来源于学院和教务系统的学生学情数据。 该数据集中包含学院4 个专业，共计1 281个学生的学情评价数据，评分从1 ～10 的整数。 根据前面的数据信息，根据相应动态学情评分，验证本文所提算法的性能和传统推荐算法性能对比分析。

2.2 基于麻雀算法改进的神经网络模型的推荐性能分析

本文采用基于麻雀算法改进的神经网络模型作为推荐算法，在该算法中参数设定见表3。 目标函数是模型训练后验证集的损失最小值；种群数量为20，迭代次数20 次，麻雀在发现者的比例设置为0.2，神经网络中神经元的搜索范围分别为［100，300］、［200，500］、［100，300］，学习率搜索范围［0.000 1，0.01］。

表4 是麻雀算法中优化的DNN 网络参数，其中隐含层的神经元参数及学习率由麻雀算法传入。

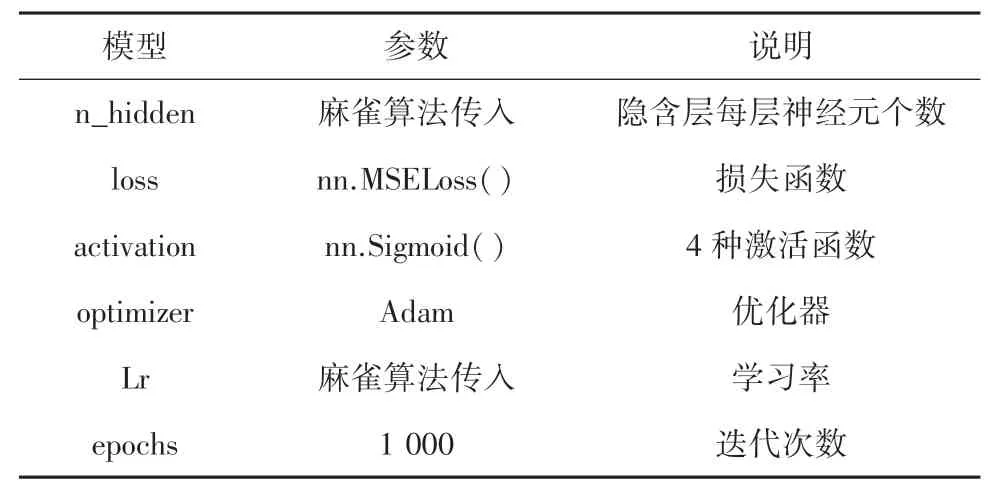
表4 麻雀算法中优化的DNN 网络参数Tab. 4 DNN network parameters optimized in sparrow algorithm

表5 是本次实验中作为对比实验的DNN 网络参数，其中隐含层的神经元设置为［100，200，100］，学习率设置为0.01。

从图12 实验结果图可知，基于麻雀算法优化的DNN 的推荐结果精准度更高，图中绿色的线是以表5 中参数设定实现的DNN 模型中目标函数值，而红色线是麻雀算法在迭代过程中的目标函数值。 可见，在经过麻雀搜索算法改进之后，具有较强的优化程度，增强了聚类效果，提升了邻间相似，最终完成了对目标用户的推荐，提高了推荐准确度。

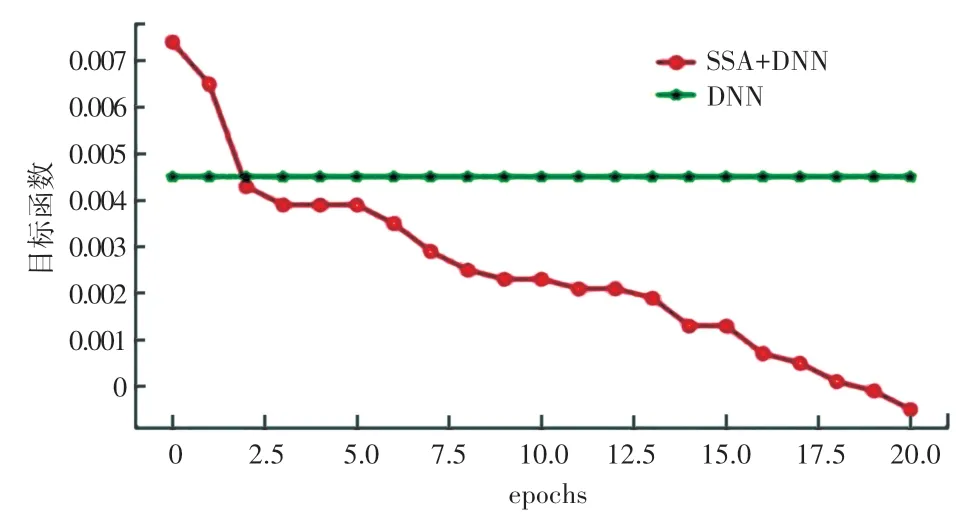
图12 基于麻雀算法优化的DNN 的实验结果图Fig. 12 Experimental results of DNN optimized based on sparrow algorithm

3 结束语

本文采用DNN 模型对基于用户画像的个性化推荐，首先对DNN 中的激活函数、梯度下降优化器的选择进行了对比实验，根据实验结果选择Sigmoid作为本文实验中的激活函数。 然后在对相关梯度下降训练集结果对比实验中，择优选择Adam 为梯度下降优化器，优化之后DNN 模型的训练集实现损失值下降速度最快，且收敛平稳；其次通过常见目标函数对麻雀算法的适用性研究，得出麻雀算法适用于优化DNN 模型。 最后采用麻雀算法对模型中的参数进行寻优，经过麻雀算法优化后的DNN 模型，在实验结果中表现出较强的优化程度，实现了更为精准有效推荐。