基于LightGBM 模型的离散制造业产品物料需求智能预测
李婷婷, 黄欣迪, 曹萌萌, 李剑锋
(中国计量大学经济与管理学院, 杭州 310018)
0 引 言
大数据驱动制造产业智能化,人工智能助力制造业数字化转型升级,随着疫情环境下制造业现有供应链脆弱性的暴露,企业原有的预测算法已不能满足制造业企业对物料需求预测的准确性。 为有效减少物料短缺与过度采购现象,助力企业降低库存成本,提高采购效率,缩短交货周期,提高企业抗风险能力,迫切需要精准度更高的预测模型[1]。
物料需求预测是指根据企业已有的销售或物料消耗数据,对企业未来一段时间内生产运营所需要的物料种类以及数量进行分析研究。 预测方法大致分为定性预测法和定量预测法。 其中,定性预测法根据预测者个人的知识、经验和主观判断,主观随意性较大,预测结果的准确度不能达到制造企业的实际需求。 时间序列分析是较为常用的定量预测法,起源于英国统计学家G.u.Yule 在1927 年提出的自回归模型(Auto Regressive,AR)[2]。 该模型与英国统计学家G.T.Walker 在1931 年提出的移动平均(Moving Average,MA)模型和ARMA 模型,构成了时间序列分析的基础,至今仍被大量应用[3]。 这三个模型主要应用于单变量、同方差场合的平稳序列,在解决线性时间序列的拟合问题上有着卓越表现。但现实中多为非线性复杂问题[4],相较于传统的时间序列预测方法,引入机器学习算法[5]可以更好地解决非线性时间序列的拟合问题。 李福等人[6]基于机器学习XGBoost 算法,对纽约市共享单车借车需求量进行了有效的预测。 李卫星等[7]使用XGBoost 算法,对4 种工况下柴油机失火故障的平均预测准确率达90%以上。 周宇阳[8]提出了一种基于机器学习SVM 算法的需求分析模型,利用该模型对沿海地区LNG 进行仿真预测。 Ntakolia,C.等[9]认为传统方法未考虑历史数据信息,因此对多种机器学习模型进行对比和校准,得到了预测准确性较高的LightGBM 算法,从而对库存系统中的延期交货率进行了有效预测。 Javad Feizabadi[5]开发了机器学习混合需求预测方法,将时间序列和解释因素都输入到开发模型中,发现了具有统计学意义的供应链改善差异。
目前,国内外需求量预测相关研究已积累了一些成果,但较少考虑离散制造业产品种类多、定货数量多等特点对需求量预测的影响,难以满足企业对预测准确性和实效性的要求。 XGBoost 算法相比其它算法收敛慢、预测耗时大、超参数多且复杂,人工调参具有较高难度,各参数的取值大小直接影响模型的预测精度,因此存在预测精度受限的问题[10-11]。 SVM 广泛应用于模式识别和回归估计等领域,与其它算法相比在解决小样本、高维非线性决策问题时有很大的优势[12],但仍然存在计算复杂、泛化能力差和过拟合等固有局限[13],在制造业需求预测问题上仍有一定的提升空间。 针对上述问题,相对于XGBoost 和SVM 算法,LightGBM 算法在样本规模较大、特征维度较高的预测任务中,呈现出计算能力强且精准度高的优势。
本研究拟采用LightGBM 机器学习集成算法对原始数据进行建模,划分训练集和测试集。 将时间序列下的物料需求量数据和库存数据输入模型进行训练,利用训练好的LightGBM 模型,在测试集上预测未来时间段内的物料需求量,同时将基于决策树的LightGBM 物料需求预测模型与传统时间序列SARIMA 模型的预测结果进行对比,为离散制造业物料需求预测问题探寻更优的预测模型。
1 实验模型
1.1 LightGBM 算法
LightGBM 算法是一种并行学习的机器学习算法,其中基于梯度的单边采样算法(Gradient-based One-Side Sampling,GOSS)和互斥特征捆绑算法(Exclusive Feature Bundling,EFB)解决了在大样本高维度数据情况下耗时长、占用内存大的问题。 本文通过构建基于Boosting 学习方式的LightGBM 预测模型,降低数据异常值对预测准确度的影响,忽略异常值权重,防止过拟合。
1.1.1 基于梯度单边采样的GOSS 算法
梯度大的样本点会贡献更多的信息增益,为了保持信息增益评估的精度,对样本进行采样时保留梯度大的样本点,对于梯度小的样本点按比例进行随机采样。 如果一个样本点的梯度小,则该样本点的训练误差就小,直接的办法就是抛弃梯度小的样本点,但该做法可能会改变数据的分布、损失学习的模型精度。 而GOSS 算法的提出,则避免了上述问题。 GOSS 算法描述详见表1。

表1 GOSS 算法描述Tab. 1 GOSS algorithm description
1.1.2 EFB 算法
LightGBM 算法不仅进行了数据采样,也进行了特征抽样,使得模型的训练速度进一步地提升,即将互斥特征绑定在一起,从而减少特征维度。 其主要思想是,在实际应用中高纬度的数据往往都是稀疏数据,故而需要设计一种几乎无损的方法,来减少有效特征的数量。 在稀疏特征空间中,许多特征都是互斥的,因此可将互斥特征绑定在一起,形成一个特征,从而减少特征维度。
EFB 算法将特征划分为更小的互斥绑定数量,是一个NP-hard 问题,即在多项式时间内不可能找到准确的解决办法。 因此,使用一种近似的解决办法,即特征之间允许存在少量的样本点并不是互斥的,允许小部分的冲突可以得到更小的特征绑定数量,更进一步地提高计算的有效性。
1.1.3 基于直方图的决策树算法
GBDT 算法由于要遍历每一个数据计算信息增益以获得最佳分裂点,时间复杂度高,而本研究样本数量非常大。 为解决该问题,Ke 等[14]提出了基于直方图的决策树算法,将连续的特征离散化为k个离散特征,也就是分桶bins思想,同时构造一个宽度为k的直方图用于统计信息(含有k个bin)。 利用直方图算法则无需遍历全部数据,只需要遍历N/k个数据即可找到最佳分裂点,极大地提高了训练效率,缩减了内存占用空间[15]。
1.1.4 带深度限制的leaf-wise 决策树生长策略
如图1 所示,level-wise 生长策略,即数据可以同时分裂同一层的叶子,容易进行多线程优化,也可以较好控制模型复杂度,不容易过拟合。 但实际上,level-wise 是一种低效的算法,很多分裂增益较低的叶子也会进行分裂和搜索,增加了计算量。
图1 level-wise 生长策略Fig. 1 level-wise growth strategy
为优化上述问题,提出leaf-wise 生长策略,如图2 所示。 决策树每次从当前所有叶子中找到分裂增益最大(一般也是数据量最大)的一个叶子,然后分裂,如此循环。 在分裂次数相同的情况下,和level-wise 相比,leaf-wise 可以得到更高的精准度。但是,leaf-wise 可能会长出较深的决策树,产生过拟合。 为解决该问题,LightGBM 在使用leaf-wise 策略时,对最大深度进行限制,在保证高效率、高精准度的同时防止过拟合。

图2 leaf-wise 生长策略Fig. 2 leaf-wise growth strategy
使用了GOSS 算法、Histogram 算法、EFB 算法的梯度提升树(GBDT) 称之为LightGBM,相较于XGBoost 等的GBDT 算法,LightGBM 的许多特性(如leaf-wise 的决策树生长策略,类别特征值的最优分割策略,数据和特征的并行学习等)都使算法的性能迅速提升[16]。
1.2 SARIMA 模型
为了验证LightGBM 模型的预测准确率,本文采用基于ARIMA 的季节性模型SARIMA(p,d,q)×(P,D,Q,s),全称为季节性自回归移动平均模型进行对比,该模型是一种常见的时间序列分析模型[17]。 其中AR 是“自回归”,p为自回归项数;I为差分,d为使之成为平稳序列所做的差分次数(阶数);MA为“滑动平均”,q为滑动平均项数;季节性序列的变化周期用s表示,对于月度序列s=12,对于季度序列s=4。
SARIMA 模型对时间序列的分析预测基本流程如图3 所示:

图3 SARIMA 流程图Fig. 3 SARIMA Flow Chart
2 实验过程与分析
本文研究的制造业原始数据集来源于美的集团,实验选取了该企业2018 ~2020 年的历史数据,实验数据集共包含1 183 594 条样本数据,其主要结构描述见表2。
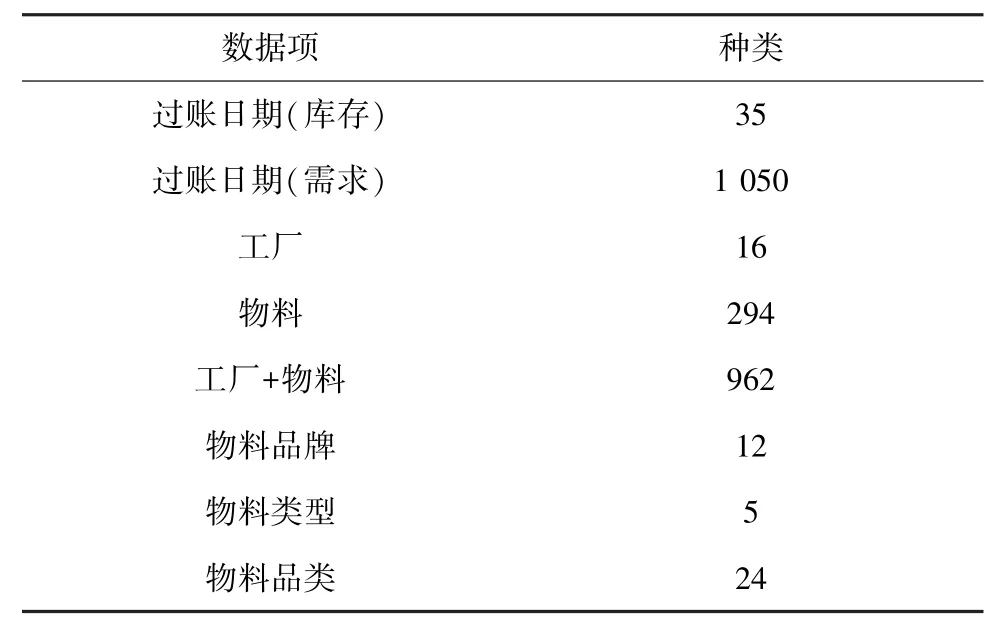
表2 实验数据集Tab. 2 Experimental data set
2.1 LightGBM 模型实验
2.1.1 数据预处理
由于制造业原始物料需求数据存在类型不一,残缺等问题,无法直接进行数据分析或建模。 为提高数据挖掘的质量及预测精准度,需在数据分析之前进行数据预处理。
2.1.1.1 数据清洗
离散制造业物料原始数据大多来源于物流单据,可能存在时间空缺、错位等问题,真实且完整的数据更有利于提高模型的预测精准度。 本研究通过数据清洗填充关键性空值数据,同时删除、更正错误或重复的数据。 结合离散制造业实际业务,原始需求量数据部分特征不能应用于预测模型,故剔除了与预测结果无关的特征。
2.1.1.2 时间切片
数据集中含有962 个“工厂编码_物料编码”组合,不能直接体现各个工厂物料具有的时间特征因素,因此选择以月为时间粒度,对现有数据进行时间切片。 一条数据包括一个月内的物料种类、物料需求量与物料库存量等。 切片后的数据从第一月开始生成对应id,见表3,作为数据的时间特征以及预测模型的影响因子之一参与模型优化。

表3 经数据清洗与时间切片后样表Tab. 3 Sample table after data cleaning and time slicing
2.1.2 特征工程
特征工程是指用一系列工程化的方式,从原始数据中筛选出更好的数据特征,以提升模型的训练效果。 特征工程通常包括数据预处理、特征选择、降维等环节。
表3 所示的数据集包含了每个工厂对不同类型物料的月需求量,直接影响目标预测变量值的因素为过账日期。 由于在构建模型时决定性特征数量较少,为使模型训练更准确,可解释性更强,研究利用统计学中的统计量,构建出新的数据特征--滑动特征和滞后特征,见表4。 构建滑动窗口特征将时间序列在时间轴上划分窗口,是常用且有效的方法,其中包括滑动窗口和滚动窗口。 窗口分析对平滑噪声或粗糙的数据非常有用,如移动平均法等。 利用这种方式结合基础的统计方法,通过对同一特征在不同时间跨度下进行分析,得到整体数据更加一般化的变化趋势。

表4 构建滞后和滑动特征Tab. 4 Build hysteresis and slip characteristics
2.1.3 实验结果及分析
为探寻每年需求量的一般规律,本研究将每个工厂、每种物料的月需求量可视化。 如图4 所示,2018~2020 年的需求趋势在时间上并未出现显著的周期性规律;2019 年3 月至6 月数据呈现较大幅度的增长,同比往年数据,2019 年末的需求量也有一定幅度的增长,数据波动较大,可能是受线上大型电器促销活动和疫情等影响;2018 年和2020 年数据增长趋势较为一致,均在6、7 月份达到峰值,较为符合消费者对于美的电器的季节性需求规律。
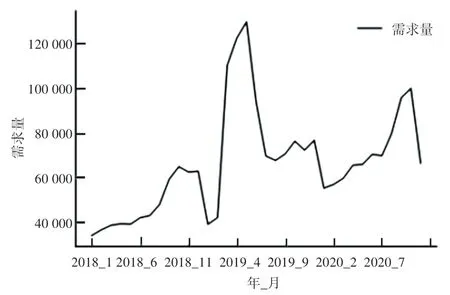
图4 月需求量曲线(2018 年1 月~2020 年11 月)Fig. 4 Monthly demand curve (January 2018 to November 2020)
基于上述分析,为预测2020 年12 月及2021 年1 月、2 月的需求量,本研究选取2018 年1 月至2019年11 月的物料需求量数据作为训练集对模型进行拟合,将2019 年12 月及2020 年1 月、2 月的数据作为验证集,来验证模型的可行性和精准度。 在此基础上对模型不断优化,最终得到拟合度较好的LightGBM 模型。
通过预测分析,将2019 年12 月部分“工厂_物料编码”组合的实际需求量(图5)和预测需求量(图6)可视化,并得出预测-实际对比需求量曲线(图7)。 可以看出,预测数据和实际数据基本一致,模型拟合度较好。
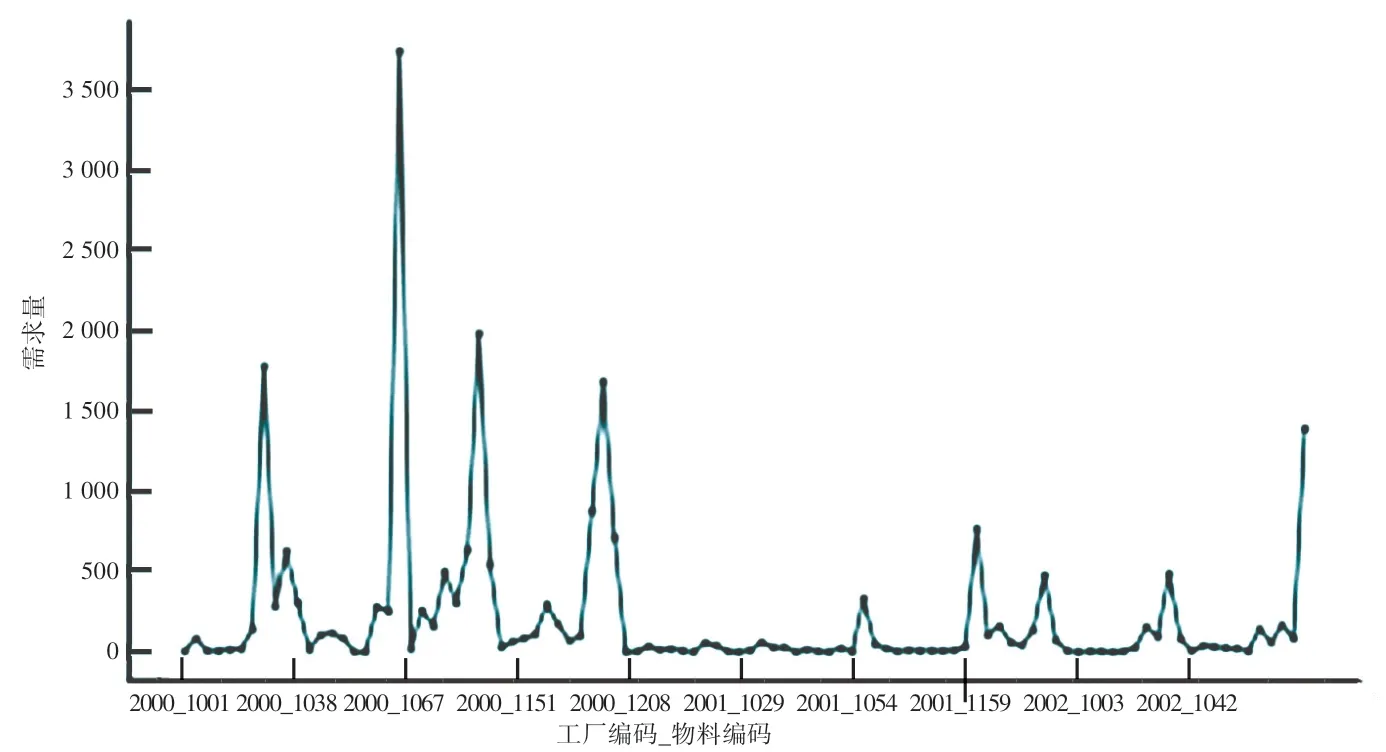
图5 实际需求量曲线Fig. 5 Actual demand curve

图6 预测需求量曲线Fig. 6 Forecast demand curve

图7 预测-实际对比需求量曲线Fig. 7 Forecast-actual demand curve
2.2 SARIMA 模型实验
2.2.1 数据预处理
SARIMA 模型适用于研究单变量在时间上的变化,而本研究需要解决多个不同工厂、不同物料随时间变化而引起的需求量变化问题,所以采用LabelEncoder 方法构建类别特征见表5。 将工厂和物料编码结合起来,从而可以对任意一个kind(类别)进行模型构建和预测。

表5 数据预处理及类别编码Tab. 5 Data preprocessing and category coding
2.2.2 数据平稳性检验与变换
为防止“伪回归”,选取工厂编码“kind =30”的时间序列进行ADF 平稳性检验,检验结果见表6。可以看出, 该工厂编码时间序列的P值为0.460 481 744 342 412 24,大于0.05,原始序列是非平稳的。 进行一阶差分后的时间序列P值为7.984 048 924 803 763e-05,小于0.05,满足平稳性。 因此,工厂编码“kind =30”的时间序列是一阶单整序列,即ps~I(1)。

表6 序列平稳性检验Tab. 6 Test of sequence stationarity
2.2.3 参数估计
从图8(ACF)与图9(PACF)中可以看出,一阶差分后的“工厂_物料”编码“kind =30”的时间序列自相关图和偏自相关图都有拖尾衰减特征,适合建立ARMA 模型。 结合表7 的参数确认方法,确认出p=1、q=1。 综上分析,采用ARIMA(1,1,1)模型进行拟合。
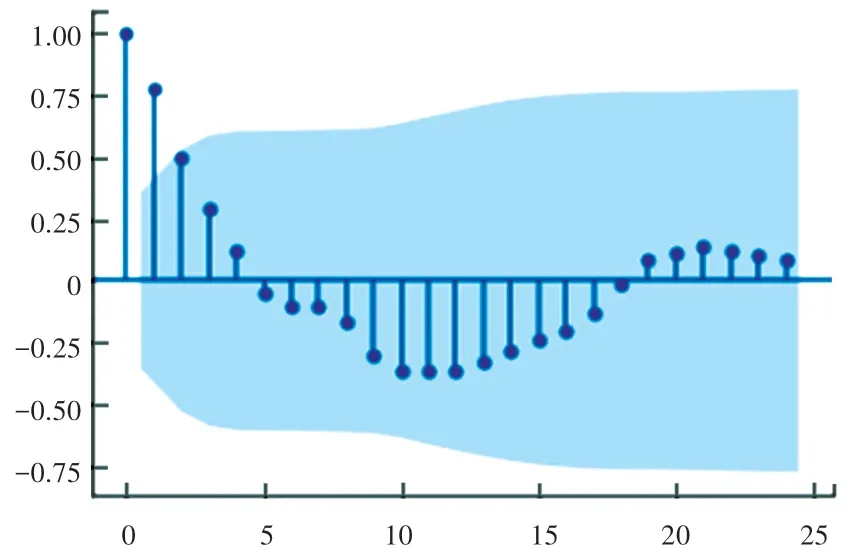
图8 自相关图Fig. 8 Autocorrelation graph

图9 偏自相关图Fig. 9 Partial autocorrelation graph

表7 参数确认方法Tab. 7 Parameter confirmation method
本实验对类别“kind =30”的数据进行季节性分解,得到原始数据的趋势、季节性因素和残差。 图10 显示出原始数据具有较明显的以年为周期的季节性特征,所以时间序列的周期s可以取12。
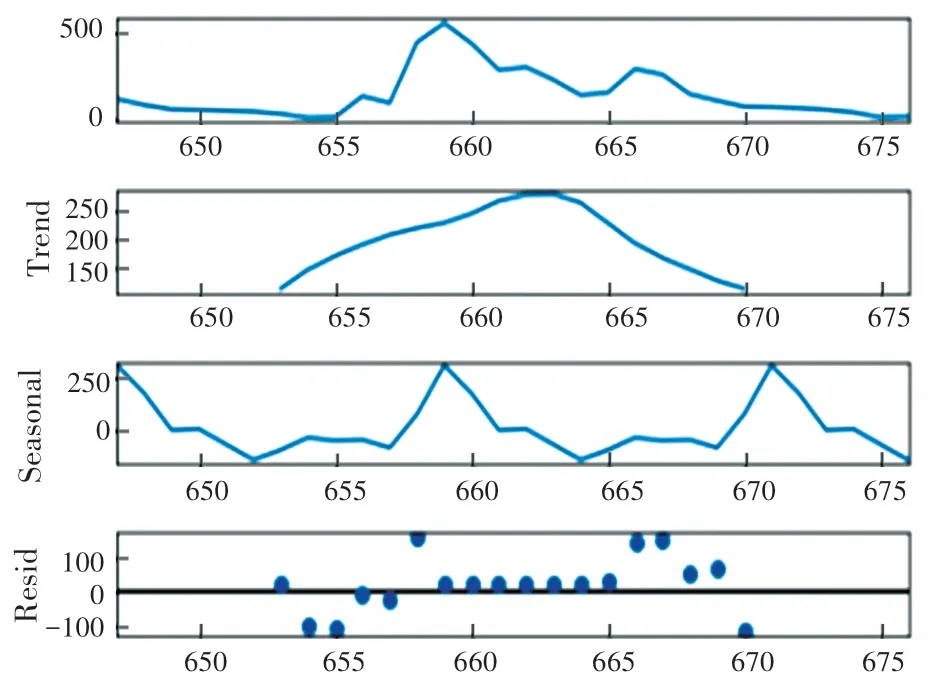
图10 季节性分解结果图Fig. 10 Seasonal decomposition results
对抽取出的季节性因素数据进行ADF 平稳性检验,得到P值为0.0,说明原季节性因素数据满足平稳性,不需要进行差分,故D=0。
根据季节性因素的偏自相关图(图11)和自相关图(图12),结合网格搜索的AIC值,确定较优的模型参数P=3、Q=1。 最终得到较优的SARIMA(1,1,1)×(3,0,1,1,2)模型。
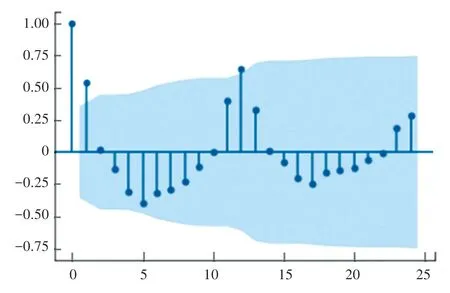
图11 季节性因素偏自相关图Fig. 11 Partial autocorrelation graph of seasonal factors

图12 季节性因素自相关图Fig. 12 Autocorrelation chart of seasonal factors
2.2.4 模型预测
利用上述确定的最优参数SARIMA(1,1,1)×(3,0,1,1,2),来拟合有效模型进行动态预测。 如图13 所示,表明该模型对需求量拟合效果较好,但从长期来看,其拟合效果存在一定偏差。
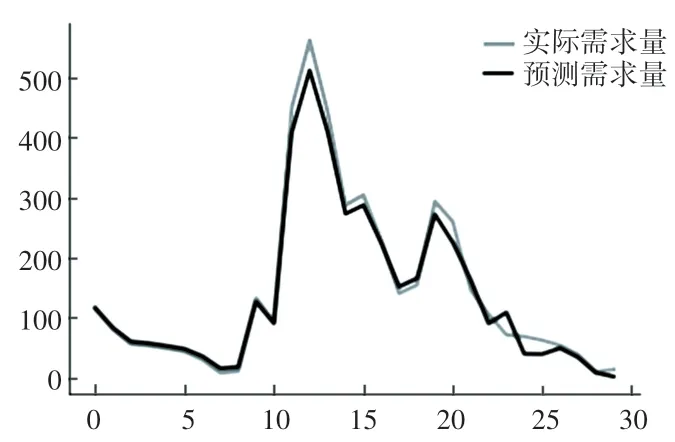
图13 SARIMA 拟合预测-真实需求量对比图Fig. 13 SARIMA fitting forecast-real demand comparison chart
2.3 模型对比分析
选取平均绝对误差MAE作为衡量两种模型预测精准度的指标,如式(1)所示。
其中,指预测值;yi指真实值;n为样本数量;MAE的范围为[0,+∞)。 当预测值与真实值完全吻合时等于0,即完美模型,误差越大,该值越大。MAE的值越小,说明预测模型拥有更好的预测精准度。
由表8 分析可知,与季节性的时间序列SARIMA 模型相比,基于决策树的LightGBM 机器学习模型平均绝对误差较小,拥有更高的预测精准度。

表8 MAE 值对比Tab. 8 MAE value comparison
3 结束语
本文以离散制造业企业美的为例,分析2018 年至2020 年的产品物料需求数据,利用基于决策树的LightGBM 机器学习模型对企业物料需求量进行预测,为了研究该模型在实际应用中的优势,构建传统时间序列SARIMA 对比模型。 对比分析实验结果表明,SARIMA 需要针对每个“工厂编码_物料编码_id”,分别进行独立建模,模型构建过程复杂、耗时较长,计算量较大,且结果显示平均绝对误差MAE大、精准度较低;基于决策树的LightGBM 机器学习模型构建过程简单、平均绝对误差MAE小、预测精确度较高,在月粒度下的短期需求预测结果满足企业实际生产的准确性和实效性要求。
LightGBM 机器学习预测模型为物料需求预测提供了科学可行的解决方案,为企业智能化管理提供了技术支持。 然而,在构建特征工程时,并未考虑到影响需求量的其他外在因素(如疫情影响、节假日、线上优惠活动等),以期在后续研究中进一步分析完善。

