双源供电的智能电网实时定价策略

高海龙， 高 岩

（上海理工大学管理学院， 上海 200093）

0 引 言

当今世界，传统能源日渐稀缺，环境问题日益严重，中国本着推动构建人类命运共同体的责任担当和实现可持续发展的内在要求，作出了力争2030 年前实现碳达峰及2060 年前实现碳中和的重大战略决策。 “双碳”目标为中国以风光发电为代表的清洁能源供电产业指明了前所未有的发展趋势。 多能源供电环境下，如何协调用电管理与定价，增进社会总福利成为影响电力行业高质量发展的重要制约因素。 智能电网基于需求侧管理的实时定价，则是解决这一制约因素的有效手段。

本文根据供电源的不同，将其划分为以风光发电为代表的清洁能源（WP）供电与以火力发电为主的传统能源（TP）供电。 清洁能源（WP）供电，虽然具有清洁环保，供电边际成本低，供应源灵活（分布广、去中心化）等优势，同时也存在易受环境气候影响，电力供应不稳定不持续等问题；而传统能源（TP）供电，虽然有环境成本高，不可再生的化石资源消耗大，发电效率低等缺点，但却有技术成熟，供电稳定，易控制输出等优势。 由此看来，两类能源供电具有高度的互补性，二者协调供电将是当今及未来很长时期内的主流能源供电模式。 不断发展清洁能源发电，提高清洁能源供电比例，弥补清洁能源供电的劣势，加快清洁能源供电技术创新，也将是未来多能源供电产业发展的主要方向。 因此，多能源供电系统的设计与研究，将是未来能源问题研究的主发方向。 文献［1］中提出了一种多能源系统的一般定价方法，将多能源价格的组成部分以时间和全时间两种方式分解，研究了价格的时间相关性，并在此基础上分析不同设施的耦合机制，从理论上研究不同能源形式价格之间的关联关系；文献［2］为智能电网设计了一种集成了多能源发电与用户的小型分布式发电和储能装置侧的实时定价策略，考虑供需双方的利益，在马尔可夫决策过程框架下，建立了实时需求响应的双层随机模型，并针对实际应用中难以集中地从用户处获取准确信息问题，提出了一种新的分布式在线多智能体强化学习算法来求解模型；文献［3］在工业园区供电系统规划中提出了一种基于前一天实时定价需求响应的分布式发电和储能系统的最佳分配策略，利用两个重要指标定量分析多能源的互补特征与规划成本之间的关系。

由文献［4］可知，基于需求响应的电力定价机制，主要包括分时电价、关键峰荷电价、自适应电价和实时电价，其中实时定价是需求侧管理最理想的电价机制。 文献［5］构建了基于效用最大化的智能电网实时最优定价模型，并提出了一种分布式算法，通过寻找每个用户的最佳能量消耗水平，以公平有效的方式实现所有用户的总效用最大化。 在此基础上，很多学者对此模型与算法进行了改进与创新，进一步有效地提升模型与算法的效率。 模型改进方面，如文献［6］电力公司通过对不同类型电力用户的电器进行分类，制定不同种类电器的用电价格，以实现引导用户在不同时段根据不同类型电器的电价来使用电器行为，进而达到削峰填谷的作用；文献［7］在用户配有新能源发电且用户用电量具有不确定性的条件下，对电器进行分类，利用相邻时段用电量之间的联系，给出一个多时段的社会福利期望最大化模型；文献［8］在社会福利最大化模型基础上，提出了一种以极小化峰谷差为目标的智能电网实时定价策略，进行实现用电需求削峰填谷的效果。 算法创新方面，如文献［9］提出了一种基于强化学习算法的在线实时定价策略，并证明了该策略能有效地实现电力需求的削峰填谷效果；文献［10］提出了一种实时定价的非线性约束优化模型，在利用KKT方程组来解决该模型过程中提出了一个基于cosh的平滑近似函数来替代非线性互补条件，进而开发了平滑牛顿算法来求解新的方程组，并证明了算法的全局收敛和局部二次收敛；文献［11］智能电网实时定价模型中，利用博弈论方法，根据电力零售市场中的电力生产商、零售商和不同类型用户，分别建立电力供应过程中同层结构主体或异层结构主体之间的多种博弈模型来进行基于需求响应的智能电网实时电价定价策略研究。

综上所述，智能电网实时定价的研究多数只局限于单能源供应，而对于多能源供电环境下的实时定价的研究较少。 本文主要研究针对不可控的清洁能源供电与可控的传统能源供电下，以社会福利最大化为目标建立实时定价模型，利用KKT 条件将该模型转化为基于影子价格的非光滑方程组，并提出一个光滑逼近函数近似代替KKT 系统中的互补条件求解影子价格。

1 系统模型

考虑一个由多能源供电组成的分层智能电网，其由一个电力供应商，两种能源供电，即以火力发电为主的传统能源供电与以风光发电为主的清洁能源供电，以及多个负载用户组成的智能电力系统。 假设在整个系统中有N个电力用户，N＝ ｛1，2，…，N｝ 表示用户集，某个用户i∈N。 用户的每个用电周期（一般为24 h）可划分为T个时间段（每段可取15 min 或30 min），K＝｛1，2，…，K｝表示时期集，某个时期k∈K。 特别地，当k＝ 0 时，则k- 1＝K。

1.1 需求侧

1.1.1 效用函数

效用是一个经济学概念，其用于度量消费者从消费商品过程中所获得的幸福感与满足感。 效用函数则是用于表示消费者消费商品数量与从中所获得的满足程度之间的关系函数。

作为一种特殊商品，电力消费效用变化除了受消费电力数量影响以外，还会因人、因时、因地而不同。 电力用户效用函数形式有很多，如文献［5］中的二次函数、文献［6］中的对数函数以及文献［12］所提出分片线性函数等，本文选用两段二次函数，形式如下：

其中，非负参数表示用户i在k时段的电力功耗，令用户偏好系数为预设参数，非负参数α预先给定。

已知，U（） 是一个分段光滑函数，当0 时，U（） 满足效用非递减性（U′（） ≥0，且U（）＝0） 与边际效用递减效应（U″（）≤0）。 如图1 所示：

1.1.2 购电支出

用户在消费电力的同时需支付相应的费用，其消费支出可表示为

1.1.3 清洁能源供电补贴

用户所消费的电力，来源于微网系统的清洁能源供电与主网系统的传统能源供电。 以风光发电为主的分布式清洁能源供电的功率比较小，且电压不稳定，无法直接使用，而储能设备的电压十分稳定，可以保证逆变器正常工作。 因此，分布式清洁能源所供应电，需用储能设备储存一期后，才能无差别于传统能源向用户输送。 因此，当期可用的清洁能源总供电如式（3）所示。 即当期稳定可用的清洁能源供电量等于所有微网系统上期清洁能源总供电量。

由于清洁能源供电具有可循环再生、绿色环保及边际成本低等优点，故无论是供电商还是公共部门，都会鼓励用户消费清洁能源所供应的电，这种鼓励措施往往表示为对清洁能源的供电消费的补贴。其补贴函数可表示为

其中，非负参数m为补贴参数。

1.1.4 需求侧福利函数

通过以上分析，电力消费的福利函数应包括消费者的福利函数、消费电力价格支付及清洁能源消费补贴，其k时段的福利函数可表示为

其中，表示k时段所有电力消费者的福利函数。

1.2 供电方

在整个交易过程中，对于供电方来说，一方面收取消费者电力消费所支付的价格；另一方面则需相应的成本。 其成本应包括：微网供电成本、并网供电成本及对消费者清洁能源发电消费补贴3 部分。

1.2.1 售电收益

供电方售电所获取的收益，应等于用户总的用电量与相应的价格乘积，即消费者电力消费的价格支付。 即：

其中，R（Xk，Pk） 表示k时段售电收益。

1.2.2 供电成本

由于供电方供电源分为两类，所以供电成本也包括清洁能源供电的成本与传统能源供电成本两部分。 即

对于清洁能源供电，其边际成本主要是电能的存储成本，比较低且固定。 故其k时段清洁能源供电成本可表示为

其中，CWP(· ) 表示清洁能源供电的成本函数；为所有用户在k时段能够使用并输送的清洁能源供电量；r则是清洁能源供电的边际成本。

主网供电主要以火力发电为主的传统能源供电，其供电成本应满足边际成本递增效用（即，随着企业的发展，生产规模超过一定界限，企业的生产材料会越来稀缺，进而单位产量的成本会逐渐上升）。因此，主网供电成本函数是一个先降后升的严格凸函数，本文采用开口朝上的二次函数模拟［3］，k时段其成本函数具体形式可表示为

其中，CTP(· ) 表示清洁能源供电的成本函数，为k时段传统能源供电量，预置参数ak ＞0 且bk≤0，ck≥0。 其示意图如图2 所示。

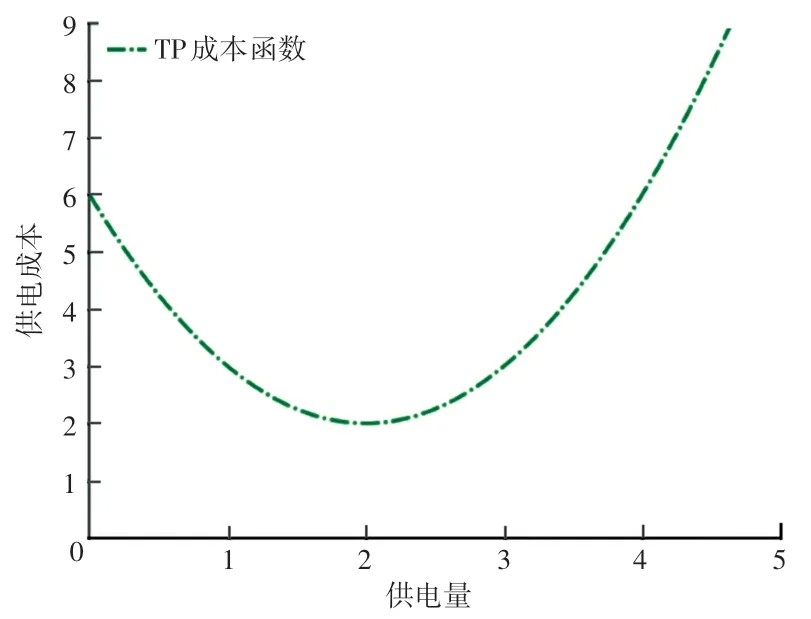
图2 传统能源供电成本函数（a ＝1，b＝-4，c＝6）Fig. 2 Cost function of traditional energy supply（a＝1，b＝-4，c＝6）

1.2.3 补贴成本

鼓励微网系统清洁能源供电消费是公共部门与供电方共同的诉求，但相应的补贴往往都是由供电方支付。 因此，k时段供电方成本应包括补贴成本，即：

1.2.4 供电方福利函数

通过以上分析，供电方的福利函数应包括供电方的售电收益，去除供电成本及清洁能源供电消费的补贴，k时段的福利函数可表示为

其中，表示k时段供给方的福利函数。

1.3 源荷约束

因受生产规模、生产环境等影响与需求的制约，k时段的电力供给量会有一个确定的区间，即：

其中，与表示用户i在k时段的最大与最小电力功耗；与表示k时段最小与最大的总供电量，分别表示所有用户最小与最大的电力功耗之和。

一个稳定的电网系统最理想状态应该是供求均衡，而电能作为一种特殊商品具有一定的公共属性，因此，电力市场供需状态最少是供能应求，而非供不应求。 即，任意时期可控的传统能源电力供应，应能足够覆盖所有用户在该时段的电力总需求与已有的清洁能源供电的电力供需缺口。 即：

则

1.4 社会福利最大化模型

在电网供需系统中，社会福利最大化应包含两方面内容：一方面则是所有的电力用户的效用和最大化，另一方面则是满足社会电力需求供应需成本最小化，因此，社会福利函数应表征这两方面内容。模型中将社会福利函数表示为所有电力用户效用函数之和与满足社会电力消费的供电成本之差。 其k时段的福利可表示为

则全周期的社会福利最大化模型可表示为：

由于各时段电力供需相互独立，因此全周期的社会福利函数最大化模型（17）等价于任意时段的社会福利最大化，即：

模型（18）解释了社会福利最大化时的最优电力供给与电力需求，虽然没有直接反映出电力的价格，但却可以在求解该模型过程中，间接地确定对应的影子价格。

2 模型求解

2.1 KKT 条件

模型（18）变形后为：

由于已知上期的清洁能源供电量， 所以当期可用清洁能源供电量为已知量。 因此，模型（19）中变量可分为两部分：用户侧k时段所有用户的电力功耗，…与供给侧的传统能源供电量。 令vk＝（，，…，，Lk）T，为模型（19）的决策变量。 传统能源供电约束≤Lk≤与用户的电力功耗约束≤xi，k≤皆为辅助约束；Wk第一项具有连续效用递减的效用函数U（·） 是一个光滑且严格凹的二次函数，第二项传统能源供电成本函数（·） 也是一个光滑且严格凸的二次函数，第三项微网供电成本函数（·） 是一个线性函数。 因此，Wk是一个光滑且严格凹的函数；已知，约束条件为线性约束，且满足线性独立约束规格；因此，问题（19）是一个光滑且严格凸的二次优化问题。 对于严格凸规划问题，肯定满足Slater 约束品性（可行域内存在“内点”），因此问题（19）可利用KKT 条件求解唯一的全局最优点。 即：

其中，是用户i在k时段最优电力功耗；k时段供电方在上期清洁能源供电量确定后，最优的总供电量其总成本函数可表示为； 而拉格朗日乘子则是反映社会福利最大化时的电力市场供需均衡的电力资源影子价格，辅助约束则无需在乘子中体现。

2.2 互补函数及光滑化处理

令函数

则互补问题：

故式 (20 ) 可转化为：

已知，函数ϕ（m，n） 在m＝n处连续但不光滑，因此方程为一个非光滑方程组。 由于传统牛顿法无法求解非光滑方程组，所以本文将采用稳定收敛且有效的拟牛顿法求解，即构造具有良好收敛性的光滑函数，逼近非光滑函数进行求解。 文献［13］给出了一致光滑逼近函数，定义如下：

定义1对于函数H·( ) ：Rn→Rn，称光滑函数Hμ·( ) ：Rn→Rn，μ ＞0 为H·( ) 的一致光滑逼近函数，如果对于任意x∈Rn， 存在k ＞0， 使得

针对非光滑函数ϕ（m，n）， 相关研究也给出了相应的光滑逼近函数，本文则给出另一个光滑函数逼近函数ϕμ(m，n) ，如下：

其中，光滑系数μ∈R＋。

证明当m≤n时，则ϕ（m，n）＝m，当m ＞n时，则ϕ（m，n）＝n，

取k≥ln2， 则即，当μ→0＋时，ϕμ(m，n) →ϕ(m，n) ，证毕。

不同的光滑系数μ对应函数ϕμ(m，n) 不同程度逼近函数ϕ(m，n) 的示意如图3 所示。

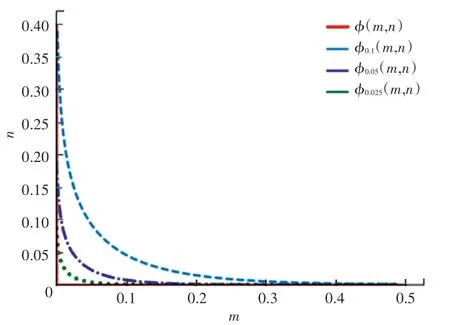
图3 光滑函数ϕμ (m，n)逼近非光滑函数ϕ (m，n)截面图Fig. 3 The cross section of smooth function ϕμ (m，n)approximating nonsmooth function ϕ (m，n)

令函数

2.3 BFGS 算法

在求解非线性方程组的众多方法中，虽然牛顿法因收敛速度快受到众多研究者青睐，但传统牛顿法有一定的局限性。 如：目标函数Hessian矩阵的正定性也难以保证，求解过程中需要计算Hessian矩阵的逆，计算量大且复杂度较高等。 为此，人们在牛顿法基础上提出了拟牛顿法。 通过构造一个正定对称矩阵代替Hessian矩阵，利用拟牛顿条件，搜索方程组的最优解。 拟牛顿条件如下：

BFGS 修正迭代法具有全局收敛性和超线性收敛速度，被认为是数值效果最好的拟牛顿法。 根据BFGS 修正迭代法，构造正定对称矩阵Bk（其中B0＝I），其迭代公式如下：

不难证明，所构造的矩阵Bk正定，其逆矩阵的迭代形式如下：

则其迭代公式为

BFGS 的形式校正算法实现过程如下：

算法步骤（∀i∈，∀t∈）

Step 1初始化x0∈Rn，μ＝μ0，精度阀值0＜ε≪1，对称正定矩阵B0＝I，k：＝0；

Step 2计算‖Φμk（λk，xk）‖， 若‖Φμk（λk，xk）‖＜ε，则停止计算，x*＝xk；

Step 3计算搜索方向

Step 4搜索最优步长

Step 5置

Step 6若则停止计算，输出x*＝xk＋1， 否则，计算

Step 7令k：＝k＋1，转至步骤3；

Step 8结束

3 模拟仿真

3.1 参数设置

设定仅有一个供电商的小型电力系统，系统中有TP 与WP 两种供电源、10 个电力用户（即N＝10）。 选择一日作为一个周期，每个周期划分为24个时段。 用户i∈N在k∈K时段的电力弹性系数在区间 [1，4] 随机产生，设置光滑系数μ＝0.1，WP 供电边际成本设置为0.01，WP 每期的发电量∈ [2，8] 随机选择，且当期固定不变。 TP 供电成本函数参数设置为ak＝0.01，bk＝ck＝0.0。 效用函数参数设置α＝0.5，初始电价∈ [0.5，1.5] 随机选取，迭代终止参数ε＝10-8。

3.2 仿真分析

通过数值仿真，计算出双源供电环境下，用户每个时段的实时电价以及对应的最优电量分配，并分别与单一传统能源供电及文献［5］所提出固定电价定价方法（λk＝ωmax-α Lk／N） 进行比较。 通过比较分析，前者相对于后两者在增加市场电力供给与需求，降低市场电价，增进社会福利方面是否有显著效果。 利用PYTHON 进行仿真，如图4 所示：

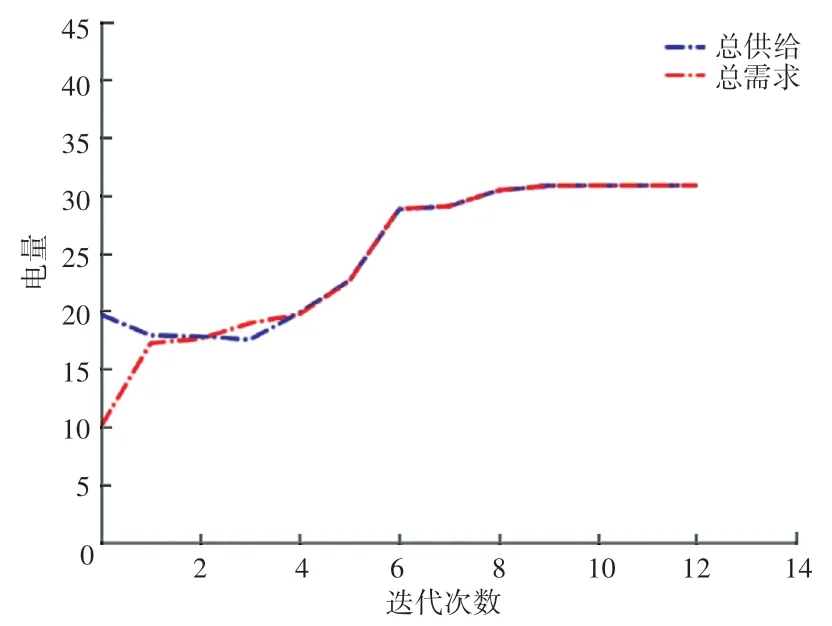
图4 某时期（ωt ＝2，＝8）供需平衡Fig. 4 Supply and demand balance in a period （ωt ＝2，＝8）

图4 给出了k时期，在双源供电背景下，参数ωk与给定，市场电力供需趋于收敛（即供需均衡，市场出清的状态）的迭代过程。 从图中可得出，模型迭代次数比较少，收敛比较快，进一步说明了此算法的有效性。 图5 则给出了双源供电环境下，整个周期市场出清时，市场总电力的供给量，传统能源的电力供给量以及清洁能源电力供给量。 很明显，清洁能源供电量相对传统能源电力供给小很多，比较符合当下电力市场供应现状。

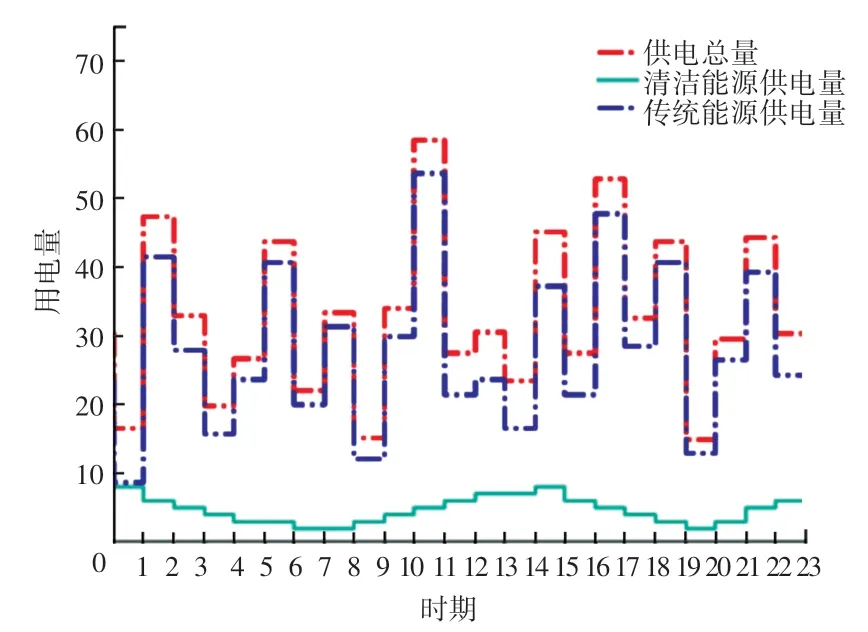
图5 ωt、与Fig. 5 ωt、and

从图6 可以看出，无论是传统的固定电价定价法还是单一传统能源供电，都比双源供电的实时定价价格要高，相应的市场电力交易量也相对要少（如图7）。 图8-图9 则给出了整个周期双源供电实时定价策略产生的社会总福利，皆高于单源供电的实时定价策略以及双源供电的固定电价策略产生的社会总福利。 因此，通过仿真可知，所提出的双源供电实时定价策略在降低电力市场电力价格、扩大市场电力交易量及增进社会福利方面有显著效果。

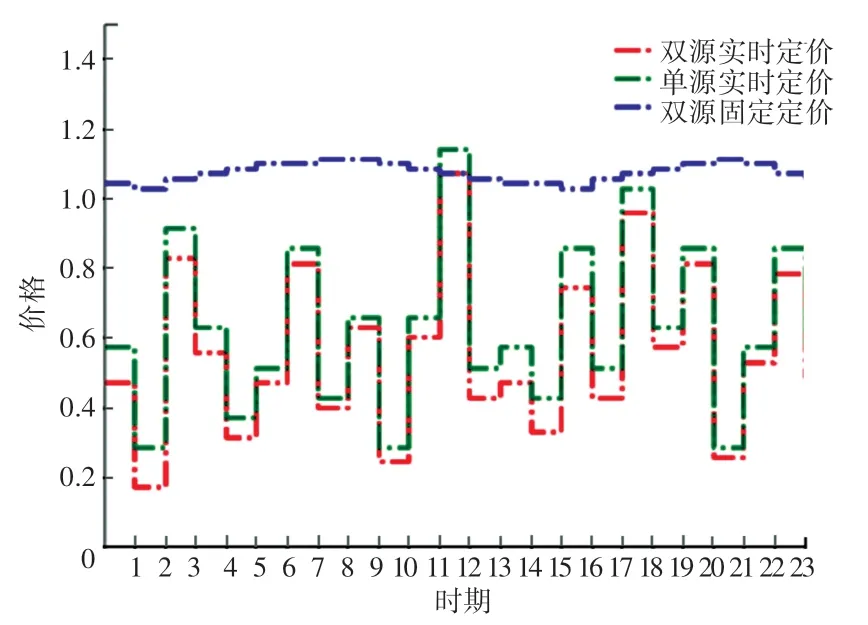
图6 电力价格比较Fig. 6 Comparison of electricity prices

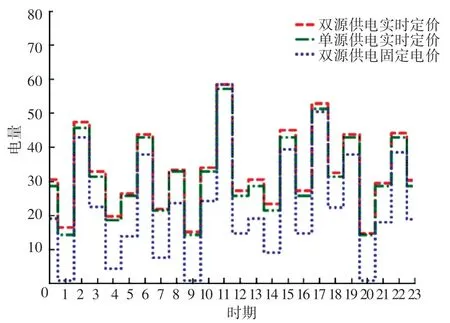
图7 市场均衡时交易电量Fig. 7 Electricity trading volume when the market is balanced

图8 社会福利比较Fig. 8 Comparison of social welfare

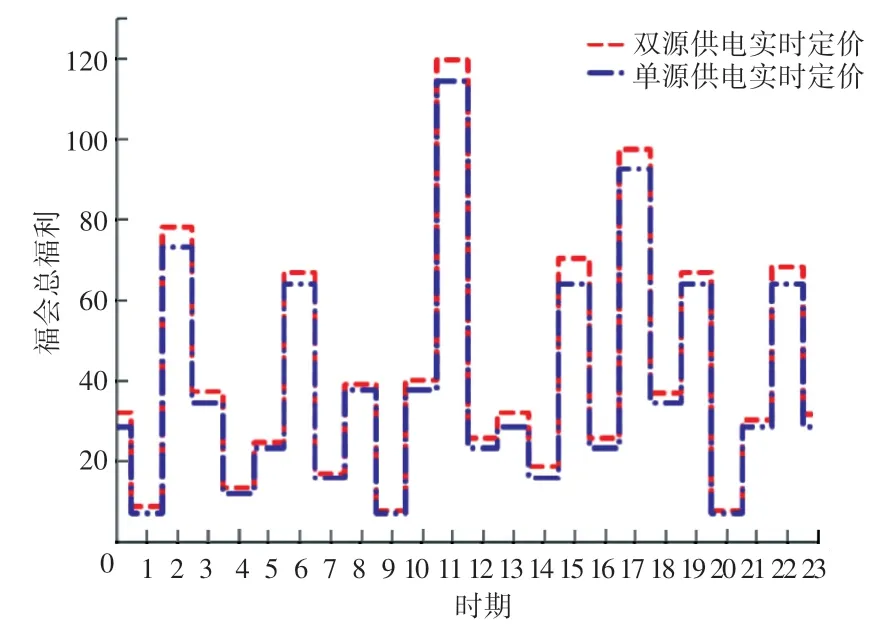
图9 社会福利比较Fig. 9 Comparison of social welfare

4 结束语

在传统能源日益紧缺的今天，保护环境、节约能源已成为一种共识。 而探索多能源协调供电实时定价，已成为能源相关研究的热点。 本文在对供电源作了两类划分基础上，提出一种实时定价策略，并验证其在增进社会福利方面的有效性与显著性。 然而这些研究并未涉及电力用户的收入约束与用户的效用分类，没有实现不同供电源供电分别定价。 因此，加入用户收入约束与实现不同供电源供电分别定价将是未来研究方向。