一种低开销与高准确度的水下定位算法

赵德腾

(云南师范大学 信息学院,云南 昆明 650500)

0 引言

目前,地球大约70%被海洋覆盖,但对海洋的探索却远不及陆地。随着陆地资源的枯竭、全球温室效应加剧等问题的出现,我国越来越重视对海洋资源的探索和海洋环境的监测。2021年,我国海洋石油的增长量占据了总增长量的8成,体现了我国加快发展海洋探索的步伐。截止到2017年,我国已经建造了多个温室监测系统,逐步完成了从南海到东海的监测,在此期间获得了大量的监测数据,为建立全国性监测系统奠定了基础。

当前,物联网技术已经发展得非常迅速,它能够把几乎所有的物体和设备都联系起来,使得多种应用能够得到有效且安全的支持。作为物联网的关键组成部分,无线传感器网络(Wireless Sensor Networks,WSNs)已经广泛应用于多种重要行业。在地面WSNs空前发展的推动下,水下传感器网络(Underwater Sensor Networks,UWSNs)在近些年也开始频繁进入大众的视野,主要用来执行海洋各区域的监测等。与在地面上不同,水下节点无法通过GPS定位且节点随海水移动,需要频繁定位。

国内外对于节点的定位研究大体上可以分为两种:一种是基于测距的,另一种是不需要测距的。前者需要先测量出未知节点与信标节点之间的距离,然后再进行节点位置的确定。后者不需要测距,利用连通性就可以实现节点位置的获取。测距技术包括:基于到达时间、基于到达时间差、基于接收信号强度指示的测距技术等。无需测距的定位算法包括[1]:质心算法[2]、APIT算法[3]、距离矢量跳(Distance Vector-Hop,DV-Hop)算法以及这些算法的改进版本等。无需测距的定位算法虽然定位精度一般,但是对硬件要求较低,能耗也较低,因此很适合大规模部署。

DV-Hop定位算法是一种低开销的定位算法,其定位准确度一般,主要用于地面WSNs的节点定位,针对其存在的不足,当前主要通过细分跳数[4-6]、跳距优化[5-6]以及采用智能优化算法寻找最优解等方法来改进[7-13]。细分跳数是通过改变信标节点的通信半径,降低跳数误差,但是会产生额外的能耗。跳距优化一般是对平均跳距进行误差修正、对未知节点采用平均跳距的方式进行改进,但依然存在提升的空间。随着智能优化算法的发展,其被大量应用到WSNs领域,尤其是通过与DV-Hop算法相结合,显著提高了DV-Hop算法的定位性能。为了进一步提高定位性能并应用于UWSNs,本文提出一种改进的DV-Hop定位算法。

1 网络模型

网络模型示意如图1所示,水下节点包括信标节点和普通节点(未知节点)。信标节点利用已知的自身位置信息,帮助未知节点进行定位。

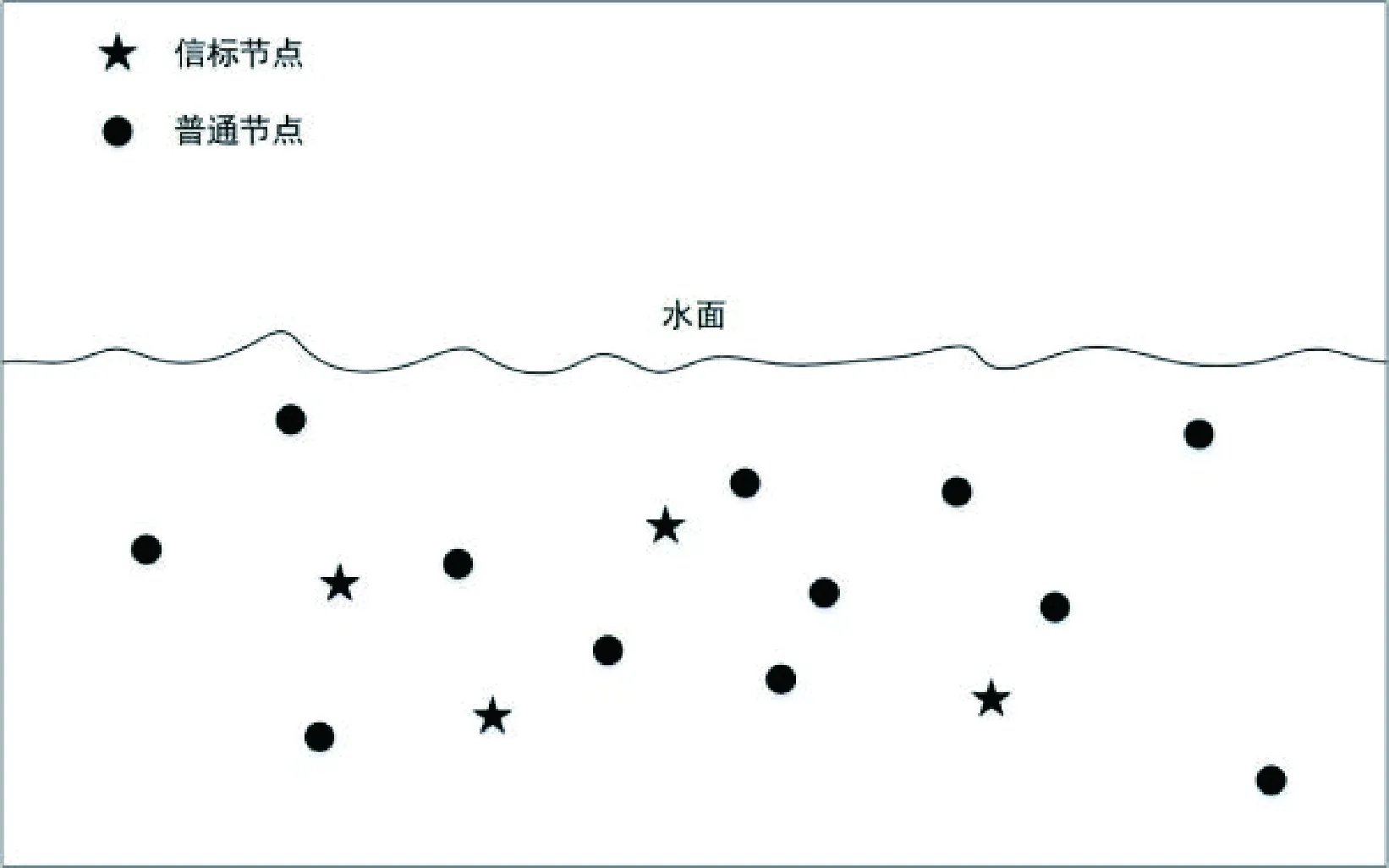
图1 网络模型示意

2 DV-Hop算法原理

DV-Hop算法的定位过程类似于基于测距的定位算法,都是在得到未知节点与信标节点之间的距离后,再进行未知节点位置的计算,不同的是,DV-Hop算法是估算距离,代价较小。

DV-Hop算法的实现可以分为3步。

(1)获取最小跳数。信标节点将包含自身坐标和跳数等信息的数据包广播到网络中,初始跳数值为0,数据包每经过一个节点,跳数值加1,最终经过对比,各节点保存到各信标节点的最小跳数。

(2)信标节点计算平均跳距和未知节点估距。

首先,信标节点计算平均跳距。信标节点利用获得的其他信标节点的坐标和两者之间的跳数信息进行平均跳距的计算,如公式(1)所示。

(1)

其中,HopSizei为信标节点i所计算出的平均跳距,(xi,yi)和(xj,yj)分别为信标节点i和信标节点j的坐标,hij为信标节点i到信标节点j的跳数。

其次,未知节点估算距离。未知节点收到最近信标节点计算的平均跳距后,与到各信标节点的最小跳数相乘,得到两者之间的距离,如公式(2)所示。

dki=HopSizei×hki

(2)

其中,dki和hki分别为未知节点k到信标节点i的估算距离和跳数。

(3)未知节点定位。

利用最小二乘法进行未知节点坐标的计算。具体计算如下所示:

(3)

其中,未知节点的坐标(x,y)(x1,y1)(x2,y2)…(xn-1,yn-1)(xn,yn)为信标节点的坐标,d1、d2、···、dn-1、dn为信标节点到未知节点的距离。之后,利用方程组的前n-1个方程分别减去第n个方程得到一个新方程组,新方程组用矩阵AX=B的形式进行表示,见公式(4)。

(4)

利用最小二乘法求出的解见公式(5)。

X=(ATA)-1ATB

(5)

3 改进的DV-Hop定位算法

原始DV-Hop定位算法存在估算的节点间距离误差较大、采用最小二乘法求解方程组可能导致无解等问题,而且复杂的水下环境会加剧定位的难度。本文通过未知节点加权估距方法和改进的粒子群优化算法提高定位性能。

3.1 未知节点加权估距

未知节点根据信标节点的平均跳距获得自己的平均跳距,原有方法仅选取离未知节点最近的一个信标节点的平均跳距,但是网络中的节点分布是不均匀的,需要针对不同情况,合理选择。因此,本文同时考虑最近信标节点的平均跳距和收到的多个信标节点的平均跳距,并进行加权计算,最终获得未知节点的平均跳距。

(6)

其中,α1、α2是权重系数,且α1+α2=1。α1、α2的计算公式分别见公式(7)和公式(8),最近信标节点和未知节点之间的跳数越多,全局平均跳距的权重越大。反之,全局平均跳距的权重越小。

(7)

α2=1-α1

(8)

其中,x是未知节点与最近信标节点之间的跳数值,C是常数。l是跳数阈值,未知节点与最近信标节点之间的跳数大于等于该阈值时,未知节点的平均跳距将只采用全局平均跳距。

3.2 改进的粒子群优化定位算法

粒子群优化(Particle Swarm Optimization)算法是一种具有高收敛速度、少参数、易实现等特点的搜索算法。粒子群优化算法的速度和位置更新公式分别见公式(9)和公式(10)。

(9)

xij(t+1)=xij(t)+vij(t+1)

(10)

其中,公式(9)的第二部分为粒子自我认知,第三部分为群体认知。t为迭代次数。c1、c2是学习因子。r1、r2为随机数。pij为个体已知最优位置,pgj为群体已知最优位置。w为惯性因子,值大则全局搜索能力强。反之,局部搜索能力强。

原粒子群优化算法陷入局部最优的可能性较大,本文提出粒子群分离的方法降低粒子群优化算法陷入局部最优的可能性,从而实现更为准确的定位。

粒子群分离:连续多轮迭代群体最优位置没有变化,则比较此时群体最优位置L1和群体次优位置L2之间的距离,如果距离超过某一阈值,则进行粒子群分离,即判断所有粒子与L1和L2两个位置之间的关系,如果当前粒子距离次优位置L2比距离最优位置L1更近,则将其从原来的粒子群中分离出来,并将分离出的粒子的群体最优位置设置为位置L2,其余粒子保持不变,分离出的粒子个数不超过Nsep。当在同一时间,分离出去的粒子的群体最优位置比主粒子群(没有分离出去的粒子)的群体最优位置更优时,重新合并粒子群。

4 结语

本文针对DV-Hop定位算法存在的问题,提出了一种改进的DV-Hop定位算法。本文通过加权估距方法降低未知节点与信标节点之间的距离估计误差,采用改进的粒子群优化算法进行位置的获取,降低算法陷入局部最优的可能性,从而实现更为准确的定位。