基于控制场的高精度相机标定技术研究
陈 洋
(中国航空工业集团公司洛阳电光设备研究所,河南 洛阳 471000)
0 引言
高精度测量技术是支撑经济高质量发展的重要技术之一,经常应用在高端制造中,是一项不可或缺的重要组成部分[1]。随着科技的进步,我国的高端制造业正在高速发展,对精密测量技术的需求也日益迫切,同时对其技术要求也不断提高,因此出现了很多新的测量需求和要求。但是传统的测量方法在面对这些新的测量需求时,测量精度已经无法有效满足应用需求,所以需要一种高精度的新测量方法来解决传统测量面临的问题[2],高精度视觉测量技术应运而生。
视觉测量具有非接触、实时测量、精度高以及可以自动化测量等优点[3-4],在高端制造业以及工业等领域需要高精度实时非接触测量等领域应用广泛。由于视觉测量的相机加工存在误差,视觉测量的精度取决于测量相机参数的标定精度,在进行测量前,要对相机的参数进行标定,用来补偿测量过程的误差。对于空间中较小的物体,在采用视觉测量时,相机参数标定往往采用高精度的平面靶标对相机进行参数标定,就能够满足测量精度;但是在对空间中大型物体进行测量时,由于测量及成像空间大,如果测量精度要求高,大尺寸的高精度平面靶标加工难度大,精度无法保证,通常采用高精度的三维靶标进行相机参数标定来保证测量精度。
本文针对大尺寸高精度测量提出了一种基于控制场的相机标定方法,并通实验证明标定方法的正确性及精度,具有较高使用价值。
1 标定方法及原理
1.1 相机成像模型
相机的成像模型可以用简单的小孔成像模型来表示,小孔成像模型中用两组参数来表示空间三维点和相机成像平面二维点之间的透视投影关系,一组参数是测量相机的内参数,一组是测量相机外参数,假设相机成像符合理想的小孔成像模型,相机内参数包括:实际焦距f、传感器像元大小(dx,dy)和图像的主点坐标(u0,v0);对于实际的成像相机模型,由于存在加工和装配等误差,除了上述参数外,相机内参数还应包括:径向畸变参数(k1,k2,k3)、切向畸变参数p1,p2;相机的外参数包括:3×3的正交旋转矩阵R和3×1的平移矩阵T。
定义OwXwYwZw为外部物体的世界坐标系,Ow为世界坐标系原点,OcXcYcZc为相机坐标系,Oc为光心,Ofuv为像素坐标系,Oxy为像面坐标系。小孔成像模型如图1所示。

图1 小孔成像模型
1.2 相机镜头畸变模型
设任意一点p的坐标为(up,vp)和(xp,yp)知:
xp=(up-u0)dx
yp=(vp-v0)dy
(1)
相机镜头的畸变模型为[5]:
(2)
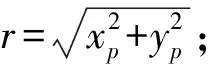
1.3 透视投影变换原理
设空间任意一点在空间世界坐标系下的坐标为(Xwp,Ywp,Zwp),齐次坐标为(Xwp,Ywp,Zwp,1),p在相机坐标系下的坐标为(Xcp,Ycp,Zcp),点p在像面坐标系下的齐次坐标为(xp,yp,1),世界坐标系到相机坐标系的旋转矩阵为R,平移矩阵为T。
由透视投影关系可以得p点世界坐标系坐标和投影点像面坐标的关系:
(3)
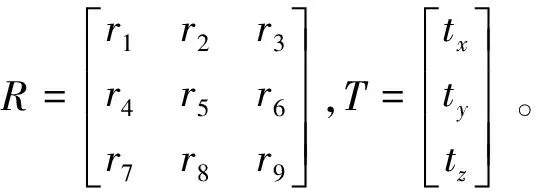
展开式(3)可以得到:
(4)
考虑相机成像畸变(4)式可写为:
(5)
1.4 构造相机参数求解模型
设空间中有n个点,在世界坐标系下的坐标为(Xwi,Ywi,Zwi),在相机像面坐标系下的坐标为(xi,yi),其中i=1,2,3,...,n。
由(5)式设:
(6)
又由旋转矩阵具有的正交性质,满足6个正交约束方程:
(7)
由式(6)(7)可以构造求解相机参数的无约束的最优目标函数:
(8)
式(6)(7)(8)中:x=[fu0v0k1k2k3p1p2r1r2r3r4r5r6r7r8r9txtytz]为待求解相机参数矩阵。
1.5 相机参数L-M优化求解流程
由最优目标函数F(x),令:
f(x)=[F11(x)...F1n(x)F21(x)...
F2n(x)H1(x)...H6(X)]r
(9)
令J(x)为f(x)的雅克比矩阵,知:
其中,i=1,2,3,...,n;j=1,2,...,6。
利用DLT求得F(x)初值x0,选取优化初始参数α>0,增长因子β>1,迭代终止条件为δ>0,且δ是很小的实数,I20×20为单位矩阵,设K=0。
利用L-M优化算法求解相机参数的具体流程如下。
步1:置α=α/β。
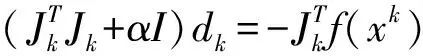
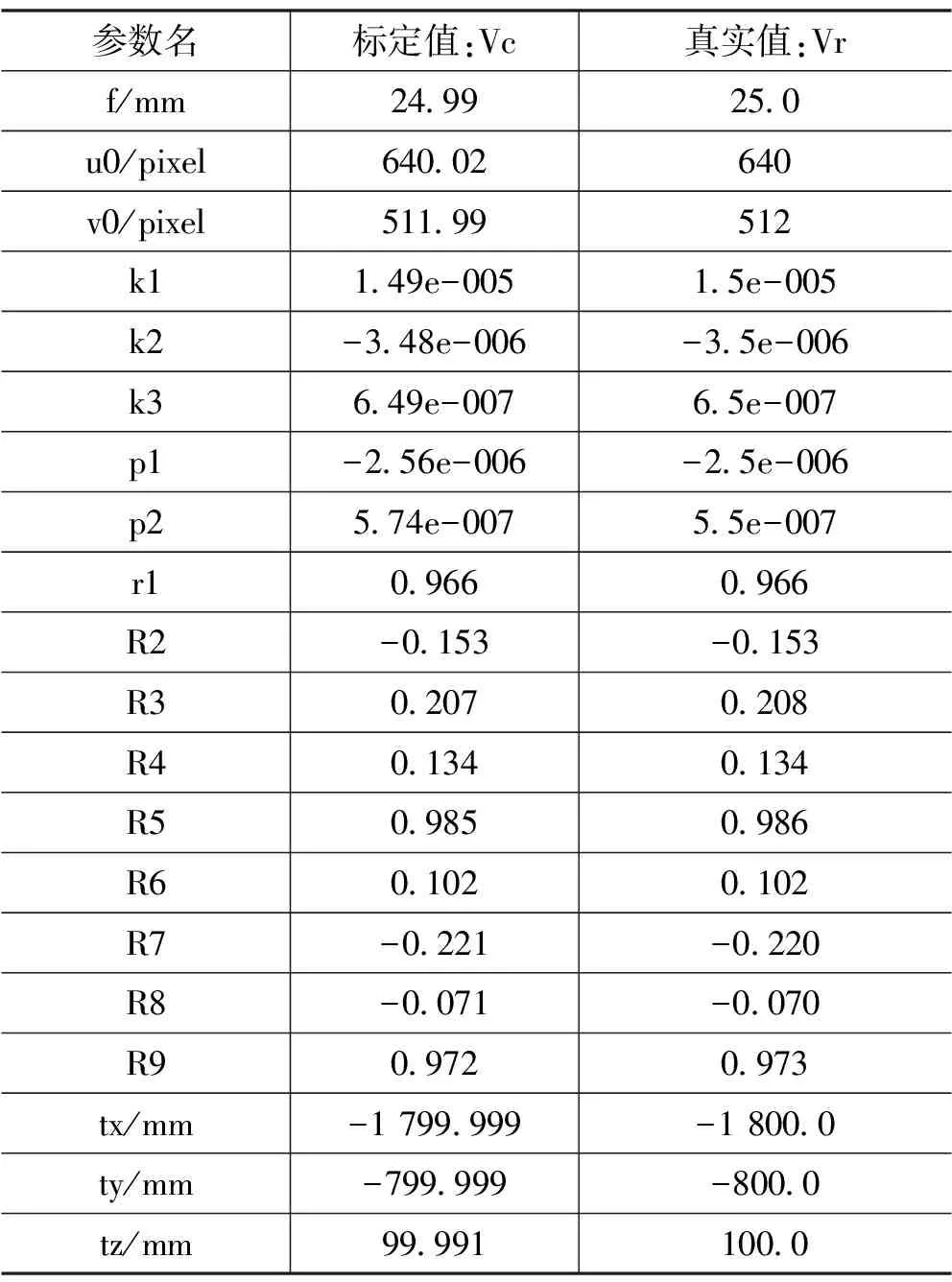
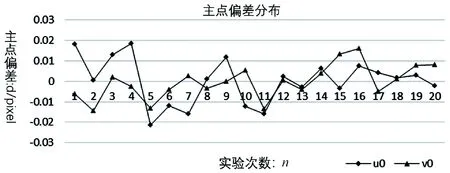
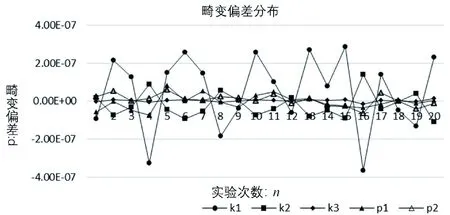
步3:若F(xk+1) 经过有限次迭代计算,可求得到相机的内外参数。 为了验证相机标定方法的正确性和高精度,构造相机模型,内参数:焦距f=25 mm;传感器x方向像元大小dx=5.3 μm,传感器y方向的像元大小dy=5.3 μm;成像大小为1 280×1 024;主点选取理论值(u0,v0)=(640,512);径向畸变:k1=1.5e-5,k2=-3.5e-6,k3=6.5e-7;切向畸变:p1=-2.5e-6,p2=5.5e-7;控制场坐标系到相机坐标系的旋转矩阵R和平移矩阵T如下式: (10) 使用本文提出的标定方法,可以计算出相机的内外参数如表1所示。 表1 相机参数对比 模拟控制场标定相机参数和相机参数真实值对比如表1所示。本算法标定值偏离真实值极小,标定值几乎与真实值相等,是因为标定过程中空间三维特征点坐标和像素二维点坐标都是根据相机成像模型仿真出的理想空间点,没有成像误差所致,实际应用过程中,由于在测量三维点时存在定位误差、控制场特征点成像时也存在二维点定位误差,实际标定结果和真实值的偏差一般会略大于理想情况下的偏差。 为了验证标定算法的稳定性,通过指定的20组不同的世界坐标系到相机坐标系的旋转平移矩阵,利用本论文标定算法计算相机内参,结果如图2—4所示。 图2 焦距 图3 主点偏差 图4 畸变偏差 由20次相机参数标定实验数据可知:20次试验标定的相机焦距平均值favg=25.000 003 51 mm,标定的相机成像主点参数偏差绝对值的平均值uavg=0.008 76 pixel,vavg=0.006 374 pixel,畸变参数标定结果偏差绝对值的平均值k1avg=1.756e-7,k2avg=5.743e-8,k3avg=5.737e-9,p2avg=2.33e-8,由20次试验结果可知相机内参标定结果具有很高的稳定型。 实际实验中使用的是灰点公司的工业相机,相机成像像素大小为1 280×1 024,相机传感器像元大小dx=dy=5.3 μm,相机镜头焦距为f=25 mm。三维控制场由8根贴有反光标志点的柱子组成,共有80个反光标志点,标志点的三维坐标已提前通过工业数字近景摄影三维坐标测量系统获得。 通过相机对控制场特征点成像,获取特征点在相机成像平面的二维像素坐标,利用本论文的标定算法获得相机内外参数。 对于三维空间中任意一点p,设其空间三维坐标为(Xwp,Ywp,Zwp),在相机坐标系下的三维坐标为(Xcp,Ycp,Zcp),像素坐标(up,vp),像面坐标为(xp,yp),世界坐标系到相机坐标系的旋转矩阵为R,平移矩阵为T,则知: (11) 由小孔成像模型知p点像面坐标: (12) 由式(1)(2)(11)(12)知p点在x、y方向的反投影误差表示为: (13) 假设空间中有n个点,则n个点在x、y方向的平均反投影误差定义为: 利用标定的相机参数计算控制场点反投影误差如图5所示。 图5 反投影误差分布 利用本论文提出的方法,利用控制场上80个特征点对相机进行标定,获得相机参数对控制场上80个特征点在x和y方向的平均反投影误差达到0.1个像素,具有较高的标定精度,可以满足空间大视场的高精度测量,具有较高的应用价值。
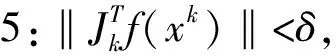
2 MATLAB仿真实验
2.1 构造相机模型及虚拟控制场
2.2 相机标定及数据分析
2.3 相机内参标定稳定性实验

3 实际标定实验
3.1 相机参数标定

4 结语

