混杂纤维超高性能混凝土力学性能尺寸效应
王 龙, 池 寅, 徐礼华, 刘素梅, 尹从儒
(1.武汉大学土木建筑工程学院,湖北武汉 430072;2.中国人民解放军陆军勤务学院,重庆 401331)
混杂纤维超高性能混凝土(HF-UHPC)是一种 新型高性能水泥基复合材料,其力学性能不仅与材料 组 分 有 关[1],还 与 材 料 尺 寸 息 息 相 关[2].对HF-UHPC 开展力学性能尺寸效应研究,揭示不同尺寸下HF-UHPC 的力学性能响应规律,对UHPC 强度预测及工程结构设计具有重要应用价值.
目前,学者们针对超高性能混凝土(UHPC)力学性能的尺寸效应进行了研究.如陈宝春等[3]和罗晨熙[4]开展了含钢纤维UHPC 抗压强度的尺寸效应研究,得到不同尺寸试件立方体抗压强度的换算关系.Fládr 等[5]发现粗骨料高强纤维混凝土抗压强度随着试件尺寸的增大而减小,且随着抗压强度的提高,尺寸效应逐渐减弱.Kazemi等[6]得到类似的抗压强度尺寸效应规律.苏捷等[7]研究了不同强度等级和钢纤维掺量对UHPC 立方体抗压强度尺寸效应的影响,得到立方体抗压强度尺寸效应规律,并建立了尺寸效应律参数的计算公式.
上述研究成果主要考虑了混凝土强度等级及钢纤维参数(掺量和长径比)对UHPC 抗压强度尺寸效应的影响,并未考虑钢-聚丙烯混杂纤维的共同作用,且对于HF-UHPC 单轴受压下的应力-应变曲线、峰值强度、峰值应变和弹性模量等力学性能尺寸效应的研究相对缺乏.因此,本文通过改变纤维参数(钢纤维掺量(体积分数)、钢纤维长径比和聚丙烯纤维掺量(体积分数)),考察了HF-UHPC 力学性能尺寸效应的变化规律,并揭示了HF-UHPC 抗压强度尺寸效应机理;同时在无切口修正的Bažant 断裂力学尺寸效应理论基础上,建立了可应用于不同纤维参数的HF-UHPC 抗压强度尺寸效应律参数计算公式,为UHPC 强度预测及工程设计提供参考.
1 试验
1.1 原材料及基准配合比
水泥为P·O 52.5 普通硅酸盐水泥;石英砂,粒径为0.4~0.6 mm;硅灰,活性指数130%;S95 级矿渣粉,活性指数105%;减水剂为聚羧酸减水剂,减水率大于35%(质量分数);拌和水为自来水.此外,2种纤维分别为:镀铜平直型钢纤维(SF),直径为0.200 mm,抗拉强度大于2 500 MPa,钢纤维长径比(lsf/dsf)为30、60、80;聚丙烯纤维(PF),直径为0.048 mm,抗拉强度大于358 MPa,聚丙烯纤维长径比(lpf/dpf)为167.结合课题组前期研究成果[8],确定HF-UHPC 基准配合比,见表1.

表1 UHPC 基准配合比Table 1 Base mix proportion of UHPC kg/m3
1.2 试验参数设计
以钢纤维掺量、钢纤维长径比和聚丙烯纤维掺量为变化因素,聚丙烯纤维长径比固定为167,设计8 种配合比HF-UHPC 试件,其纤维参数如表2所示.分别制作边长为70.7 mm(A 组)、100 mm(B 组)、150 mm(C组)、200 mm(D组)的4种立方体试件和70.7 mm×70.7 mm ×212.1 mm(E 组)、100 mm ×100 mm ×300 mm(F 组)、150 mm ×150 mm×450 mm(G组)、200 mm×200 mm×600 mm(H组)的4种棱柱体试件.除B、F 试件各制作2 组外,其他尺寸试件各制作1 组,每组3块试件,共计240块试件.

表2 HF-UHPC 试件的纤维参数Table 2 Fiber parameter of HF-UHPC specimens
1.3 试件制备及加载
试件制备步骤如下:(1)依次称取各组分材料;(2)将水泥、矿渣粉、硅灰及石英砂加入搅拌机,搅拌5 min;(3)将水、减水剂及聚丙烯纤维混合均匀,分2 次加入搅拌机,搅拌5 min;(4)均匀撒入钢纤维,搅拌5 min,以保证混合均匀;(5)搅拌结束后,将混凝土倒入模具中振捣1 min,模具表面覆盖保鲜膜;(6)常温养护24 h 脱模,放入45 ℃的养护室内蒸汽养护28 d.
依据GB/T 31387—2015《活性粉末混凝土》进行试验加载,其中A、B、E、F 组试件采用2 500 kN 的MTS 压力试验机,其余组别试件采用30 000 kN 电液伺服压力试验机.立方体抗压强度试验采用荷载控制,加载速率为1.2 MPa/s;轴压力学性能试验采用位移控制,加载速率为0.002 mm/s,通过位移计和压力传感器测量试件的载荷-位移曲线.
2 试验结果及分析
2.1 立方体抗压强度尺寸效应分析
图1 展示了HF-UHPC 试件的立方体抗压强度平均值,立方体抗压强度变异系数小于4.05%,表明试验数据离散程度较低.由图1 可知,相同配合比HF-UHPC 的立方体抗压强度存在显著的尺寸效应,并随着试件尺寸的增大而逐渐降低.例如,当HF-UHPC 配合比为SA2PA10 时,边长为100、150、200 mm 立方体试件的抗压强度较边长为70.7 mm 试件分别下降了5.46%、11.69%、16.49%.

图1 HF-UHPC 试件的立方体抗压强度Fig.1 Cube compressive strength of HF-UHPC specimens
2.2 单轴受压力学性能尺寸效应分析
2.2.1 应力-应变全曲线尺寸效应
通过对不同尺寸、不同纤维参数的HF-UHPC棱柱体试件进行轴压力学性能试验,发现其应力-应变(σ-ε)曲线变化过程基本相同,均包含弹性阶段、裂缝稳定发展阶段、裂缝失稳扩展阶段和破坏阶段.以配合比为SC2PA10 的不同尺寸棱柱体试件为例进行分析,其应力-应变曲线如图2 所示.结合文献[9]对试件受压全过程力学性能尺寸效应进行分析:
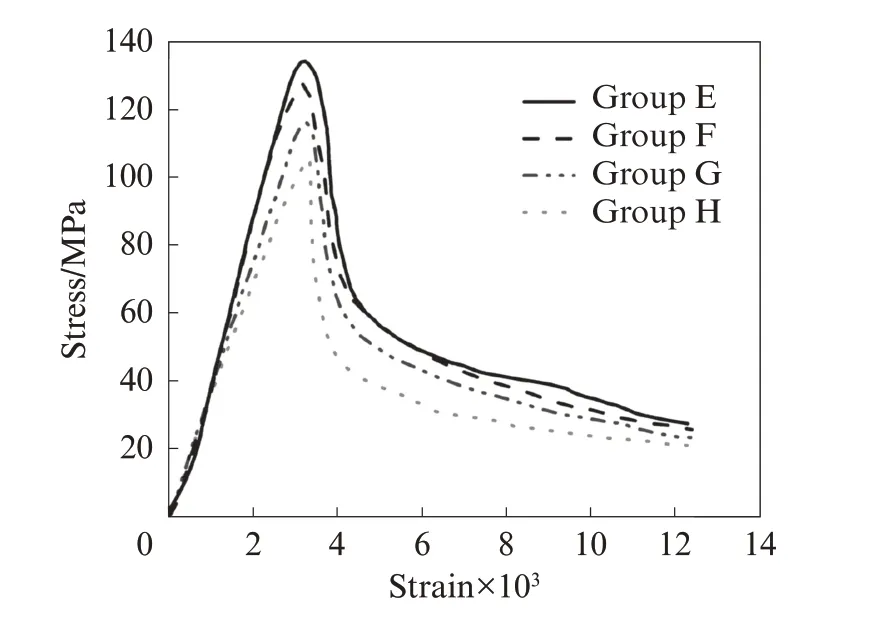
图2 HF-UHPC 棱柱体试件的应力-应变曲线Fig.2 Stress-strain curves of HF-UHPC prism specimens
(1)弹性阶段(σ≤70%fc(峰值强度)) 该阶段,各HF-UHPC 试件的应力-应变关系均呈线性增长趋势,且应力-应变关系曲线斜率(即弹性模量)基本相同,与试件尺寸无关.该阶段混凝土的变形主要为试件本身受压后的弹性变形,未产生微裂纹和裂缝.
(2)裂缝稳定发展阶段(70%fc<σ≤fc) 该阶段,各HF-UHPC 试件的应力-应变全曲线呈现较为明显的非线性特征,尺寸效应逐渐显现.具体表现为:小尺寸HF-UHPC 试件的切线刚度高于大尺寸试件,且随着试件尺寸的增大,切线刚度的差异性逐渐增加;HF-UHPC 试件的峰值强度随着试件尺寸的增大呈现规律性降低,峰值应变随着试件尺寸增大呈现规律性升高.
(3)裂缝失稳扩展阶段(fc>σ≥40%fc) 该阶段,各HF-UHPC 试件的应力-应变曲线向下弯曲,试件出现贯通裂缝,裂缝间的聚丙烯纤维逐渐被拉断,钢纤维逐渐被拔出;此阶段受压试件尺寸越大,峰后应力-应变曲线下降越快,原因在于裂缝扩展速率与试件尺寸有关,且在很大程度上随着试件结构尺寸的平方而增加[11],从而导致应力-应变曲线下降段更加陡峭.
(4)破坏阶段(40%fc>σ) 该阶段,试件的贯通裂缝在剪应力作用下不断发展加宽,钢纤维继续被拔出,聚丙烯纤维继续被拔断,试件整体失去结构意义.从HF-UHPC 试件的应力-应变曲线所围面积可以看出,HF-UHPC 试件尺寸越小,韧性越大,试件破坏吸收的能量值就越高.
2.2.2 关键力学性能指标尺寸效应
图3展示了不同尺寸HF-UHPC 棱柱体试件的关键力学性能指标平均值,其中峰值强度、峰值应变和弹性模量的变异系数分别小于4.75%、7.43%、5.30%,表明试验结果离散性较小.由图3可知:HF-UHPC 棱柱体试件的峰值强度和峰值应变存在尺寸效应,且随着试件尺寸的增大,峰值强度逐渐降低,峰值应变逐渐增大,弹性模量尺寸效应不明显,可以忽略.例如,HF-UHPC 配合比为SA2PA10时,尺寸为100 mm×100 mm ×300 mm、150 mm ×150 mm ×450 mm、200 mm×200 mm×600 mm 的棱柱体峰值强度较尺寸为70.7 mm ×70.7 mm ×212.1 mm 的棱柱体分别下降6.29%、13.15%、17.70%;峰值应变分别升高3.40%、5.82%、7.61%;弹性模量变化幅度较小,分别升高1.23%、下降1.18%、升高0.99%.

图3 HF-UHPC 棱柱体试件的关键力学性能指标Fig.3 Key mechanical performance indexes of HF-UHPC prism specimens
3 尺寸效应规律分析
3.1 纤维参数对尺寸效应的影响
引入尺寸效应度[7]对HF-UHPC 的力学性能尺寸效应进行定量分析.以边长70.7 mm 的立方体试件和70.7 mm×70.7 mm×212.1mm 的棱柱体试件为基准试件,其余尺寸试件为非基准尺寸试件进行分析.HF-UHPC 试件的立方体抗压强度尺寸效应度(Δαx)、峰值强度尺寸效应度(Δβx)和峰值应变尺寸效应度(Δrx)计算公式如式(1)~(3)所示.
式中:fcu,70.7、fcu,x分别为边长为70.7 mm 和xmm 试件的立方体抗压强度,MPa;fc,70.7、fc,x分别为70.7 mm×70.7 mm×212.1 mm 和xmm×xmm×3xmm 棱柱体试件的峰值强度,MPa;ε70.7、εx分别为70.7 mm×70.7 mm×212.1 mm 和xmm×xmm×3xmm 棱柱体试件的峰值应变;x表示试件的长度,分别取为100、150、200 mm.
图4 为HF-UHPC 试件的力学性能尺寸效应度.由图4 可知:随着钢纤维掺量或钢纤维长径比的增大,HF-UHPC 的立方体抗压强度、峰值强度和峰值应变尺寸效应度呈现增大趋势;随着聚丙烯纤维掺量的增大,HF-UHPC 的立方体抗压强度、峰值强度和峰值应变尺寸效应度先减后增,变化幅度较小.例如,相比钢纤维掺量为1%的HF-UHPC,钢纤维掺量为2%、3% 的HF-UHPC 力学性能尺寸效应度Δα100增 加11.20%、42.86%,Δβ100增 加21.45%、35.91%,Δγ100增加23.99%、30.21%;相比钢纤维长径比为30 的HF-UHPC,钢纤维长径比为60、80 的HF-UHPC 的Δα100增加14.13%、37.22%,Δβ100增加13.83%、22.92%,Δγ100增加8.32%、30.84%;相比聚丙烯纤维掺量为0%的HF-UHPC 试件,聚丙烯纤维掺 量 为0.05%、0.10%、0.15%HF-UHPC 试 件 的Δα100减小6.57%、7.45%、2.65%;Δβ100减小3.56%、4.30%,增加1.82%;Δγ100减小6.40%、8.22%,增加2.54%.
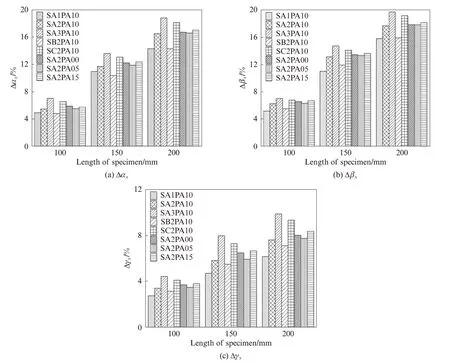
图4 HF-UHPC 试件的力学性能尺寸效应度Fig.4 Size effect parameter for mechanical property of HF-UHPC specimens
3.2 抗压强度尺寸效应机理
裂缝产生过程中能量释放率和能量吸收率间的不匹配是混凝土存在尺寸效应的根源,且能量释放率很大一部分随着试件尺寸平方的增加而增大,能量 吸 收 率 则 随 试 件 尺 寸 线 性 增 大[10].图5 为HF-UHPC 抗压强度尺寸效应产生机理示意图.由图5(a)可见:当试件处于临界失稳阶段时,能量释放率等于能量吸收率[11];相比小尺寸试件,大尺寸试件能量吸收率虽有所增大,但其能量释放率增速更加显著,致使大尺寸试件的相对裂缝深度(a/D)小于小尺寸试件,从而导致失稳破坏提前,产生抗压强度尺寸效应.由图5(b)可见:钢纤维在裂缝区起到桥接作用,能够有效抑制裂缝的展开,并不断消耗能量;由于小尺寸试件相对裂缝深度更大,裂缝间“有效”作用的钢纤维更多,纤维的增强作用更加明显,导致HF-UHPC 抗压强度尺寸效应愈发显著;随着钢纤维掺量或钢纤维长径比的增大,不同尺寸试件的纤维增强作用差异增大,裂缝宽度比增加,导致HF-UHPC 抗压强度尺寸效应更加显著.由图5(c)可见:聚丙烯纤维主要作用于断裂过程区,可有效抑制微裂纹的扩展并消耗能量,但由于临界失稳阶段断裂过程区长度与试件尺寸的比值为定值[12],导致体积分数相同的聚丙烯纤维对几何外形相似的试件增强效果相同;另外,聚丙烯纤维为低弹性模量材料,对试件的抗压强度影响较弱.因此,随着聚丙烯纤维掺量的增加,HF-UHPC 抗压强度尺寸效应度相对略微下降;当聚丙烯纤维掺量过多时,混凝土内部易形成薄弱点,削弱试件的力学性能,反而会加剧HF-UHPC 抗压强度尺寸效应.
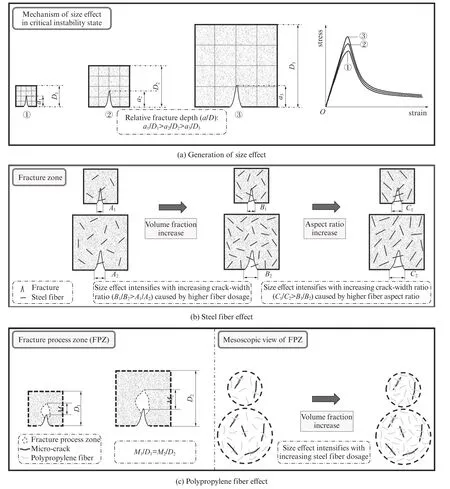
图5 HF-UHPC 抗压强度尺寸效应产生机理Fig.5 Mechanism of size effect on compressive strength of HF-UHPC
3.3 尺寸效应律
Bažant[10]引入无穷大名义强度(f∞r)和边界层开裂有效厚度(Db)这2 个参数,得到材料失效时的名义强度尺寸效应律,即无切口修正的Bažant 尺寸效应律公式:
式中:σN为受压破坏时的名义强度;D为立方体边长或棱柱体高度.
将试验得到的HF-UHPC 立方体抗压强度及棱柱体峰值强度实测值σN代入式(4)中进行拟合分析,得到不同配合比下HF-UHPC 抗压强度尺寸效应律公式的参数值f∞r和Db.HF-UHPC 试件的尺寸效应拟合参数及相关系数见表3.基于表3 数据,建立HF-UHPC 尺寸效应律公式参数与抗压强度及钢纤维和聚丙烯特征参数(λsf、λpf)的关系,其关系式见式(5)~(8).

表3 HF-UHPC 试件的尺寸效应拟合参数及相关系数Table 3 Size effect simulation parameter and correlation coefficient of HF-UHPC specimens
式中:fcu,100、fc,100分 别为标 准试件 的立方 体抗压强度和轴心抗压强度;λsf=φsf×lsf/dsf;λpf=φpf×lpf/dpf.
通过上述关系式可以定量分析纤维参数对HF-UHPC 抗压强度尺寸效应的影响程度,即不同纤维参数下HF-UHPC 抗压强度随尺寸变化的规律.利用式(5)~(8)对文献[3-4,7]进行HF-UHPC 抗压强度尺寸效应分析,将其立方体抗压强度预测值与试验值进行对比,如图6 所示.图6 显示精确度大于91.5%,表明式(5)~(8)预测精确度较高.

图6 HF-UHPC 抗压强度预测结果和实际结果对比Fig.6 Comparison between compressive strength predicted results and actual results of HF-UHPC
4 结论
(1)HF-UHPC 立方体抗压强度和轴心抗压强度均存在显著的尺寸效应.该尺寸效应随着钢纤维掺量或钢纤维长径比的增大而增大;随着聚丙烯纤维掺量的增大呈现先减后增趋势,且变化幅度较小.
(2)HF-UHPC 轴心受压峰值应变存在显著的尺寸效应.该尺寸效应随着钢纤维掺量或钢纤维长径比的增大呈现增大趋势;随着聚丙烯纤维掺量的增大呈现先减后增趋势,且变化幅度较小.HF-UHPC弹性模量尺寸效应可以忽略不计.
(3)基于无切口修正的Bažant 断裂力学尺寸效应理论,建立了尺寸效应律参数f∞r和Db的计算公式,可用于不同尺寸、不同纤维参数HF-UHPC 抗压强度的计算.

