仿生六足机器人柔顺腿研究

王 伟 韦 浪 刘富盛 王国顺

武汉大学动力与机械学院,武汉,430064

0 引言

足式机器人在非结构化环境中有优越的适应能力,相比轮式、履带式机器人具有更好的发展前景[1]。尽管近年来足式机器人性能越来越强,然而目前为止,足式机器人与足式动物之间在能量输出效率、运行速度、灵活性以及稳定性上仍然存在巨大的差距[2]。

研究发现,自然界中的足式动物在运动时会主动调节腿的刚度以适应不同的自然环境和运行速度,其腿部一般具有储能功能,可以主动储存和释放能量,使得运动效率显著提高,同时节省了体力[3]。许多足式动物的肌肉-骨骼系统可以视作弹簧进行研究,进而指导人们设计对应的仿生机器人系统[4-6],为了模仿动物腿部的柔顺行为,国内外已经展开了大量研究。波士顿动力公司开发的BigDog四足机器人[7]、意大利理工大学开发的HyQ四足机器人[8]以及我国北京理工大学[9]和重庆大学[10]开发的液压驱动四足机器人均采用了液压驱动的腿部,可以很好地解决外界冲击和自身振动的问题,实现主动柔顺控制,然而由于液压系统通常对制造、装配等要求较高,机构复杂度较高且后期维护不便,因此不适于小型化应用。西北工业大学为四足机器人开发了刚-柔复合的腿部,能够实现连续垂直跳跃,腿部弹性环节能够起到缓冲作用,方便机器人在恶劣环境下运行[6]。重庆大学设计了一款连杆-线驱动的腿部,使用弹簧作为缓冲元件,有效地减小了着地时的冲击力[10]。此外,为了模仿动物的动态运动,研究人员开发了许多具有柔顺腿的足式机器人,如ScoutⅡ[11]、Sprawlita[12]和RHex[13]等,它们在与地面接触时可以分为减速段和加速段,减速段储存能量,加速段释放能量,从而能够实现基于弹簧负载倒立摆(spring loaded inverted pendulum,SLIP)模型的动态运动。

由此可见,腿部柔顺性对提高足式机器人运动性能和环境适应性有极大的帮助。在研究仿生六足机器人的过程中发现,三角步态下当两组腿的运行速度较快时会出现整体的腾空相,并且在合适的参数范围内稳定性极强,前进速度较高。理论上完全刚性的腿在与地面碰撞时因为缺乏柔顺性会对机体的冲击较大,同时存在大量的能量损耗,因此不会出现连续稳定的腾空相。

由于仿生六足机器人的弧形腿使用复合材料(玻璃纤维)制成,其本身可以看作弹性元件,在与地面交互时腿部会由于外力而压缩并储存能量,腿部离开地面时释放能量,造成机器人具备短暂的腾空相位,这极大地提高了运行速度,同时具备节能效应。然而如何描述弧形腿的刚度以及弧形腿的刚度对仿生六足机器人的具体影响如何变化仍然是未知的,因此,本文将首先探索描述弧形腿刚度的数学模型,然后致力于探索弧形腿的柔顺性对六足机器人运动速度和有效能量利用率等方面的具体影响。

1 弧形腿刚度分析

弧形腿在外力作用下的变形是一个典型的非线性行为,其刚度建模存在许多挑战,需要选择一种好的建模方法,对该方法的需求包括:①准确地描述弧形腿弹性行为,当弧形腿受力时每一点的位移大小和方向都能通过该方法准确描述;②能够很好地融入机器人动力学,在机器人动态奔跑时能捕捉其动态特性,也即从静态和动态两方面描述腿的柔顺属性。

弧形腿的变形通常较大,因此材料力学中的小变形假设不再适用,柔顺机构学中的大变形理论可以很好地描述这种行为。弧形腿矢状面的刚度可以用伪刚体模型给出,图1所示为伪刚体近似过程和相关参数设置,根据柔顺机构学的思路,弧形腿可以视作初始弯曲的悬臂梁[14],其曲率大小与弧长相关,可以用一个量纲一量k0表示为k0=lRi,其中l为变形位置到加载点的弧长,Ri为弧形腿半径,则刚度可以表示为

图1 伪刚体模型参数设置

(1)

其中,Kt为扭簧刚度,Kθ为刚度系数,E为材料的弹性模量,Is为矢状面的截面惯性矩。对于直悬臂梁,Kθ表示负载施加角度的函数,弧形腿的Kθ可以通过k0近似取得。ρ为特征点与接触点的距离,通过接触点可以得到特征点(特征铰链)的位置,且ρ还可表示为伪刚体杆的长度。不同k0值下,ρ、Kθ的取值见表1。HOWELL等[15]于1996年在初始弯曲梁的研究中已经给出了详细的参数对照表。因此,只要弧形腿的材料和尺寸参数(E,Is,Ri,l)确定,就可以通过式(1)直接得到扭簧刚度Kt,该模型很好地表征了弧形腿的变刚度特性,随着加载点的变化(即l的量值变化),弧形腿具有不同的刚度,同时,从该模型中可以提取出刚度控制参数,从而在制造时通过这些参数改变弧形腿的刚度。

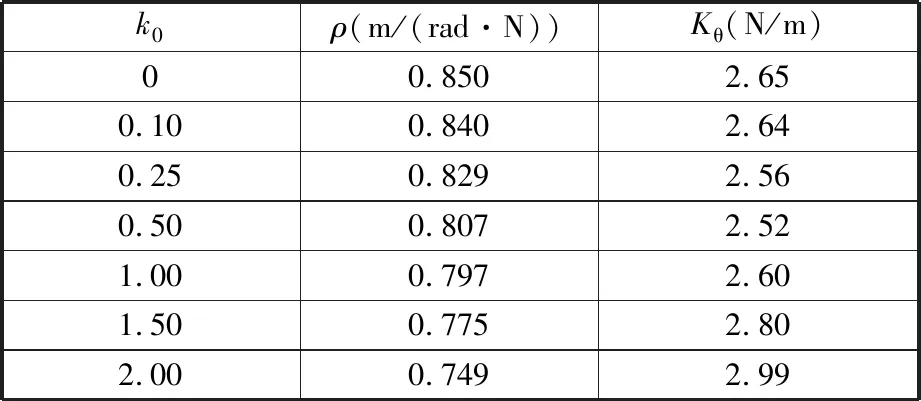
表1 不同k0值下的ρ、Kθ值

2 仿真研究

通过虚拟样机仿真的方式模拟机器人和传感器的应用有助于缩减成本、简化设计流程并缩短开发时间,通过仿真可以验证机器人的运动学和动力学特性、验证轨迹生成方法的有效性并开发不同的步态。

基于对弧形腿刚度的近似,在Webots中建立的仿真模型如图2所示,使用简化的六足机器人模型以提高计算速度,只保留机身和用于驱动的弧形腿要素,在建模时将弧形腿分成两段,两段腿之间添加扭簧模块表示弧形腿的刚度,刚度系数可以调节至无穷大表示完全刚性的弧形腿。仿真模型的参数如下:机身质量10 kg,基体长度L=634 mm、宽度W=244 mm、厚度H=125 mm,为避免运动干涉,中间腿宽度(即机器人最宽处)设为466 mm,仿真过程中不考虑弧形腿与地面间的滑移,摩擦因数设为1。

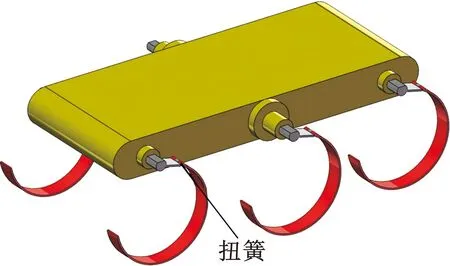
图2 虚拟样机仿真模型

2.1 步态控制策略

本文主要在跳跃步态和三角步态下研究柔顺腿对仿生六足机器人运动的影响,其中跳跃步态更能反映机器人的动态行为,三角步态下机器人可以容易地调整姿态。如图3所示,跳跃步态下6条腿的状态变化一致,可以使用单腿控制器控制。图4所示为单腿控制器参数描述,控制参数包括4个,分别为期望的触地相时长t1、触地角度θ0、离地角度θ1和整圈周期T,每个步态周期内根据弧形腿是否与地面之间存在接触分为速度较慢的着地相和速度较快的腾空相[16]。

(a)跳跃步态 (b)三角步态

图4 单腿控制器

三角步态下每组腿的相位转换与单腿运动一致,它在一个周期内的位置和速度通过周期性的时钟函数Buehler时钟控制,三角步态下两组腿之间的相位差为π,控制器参数如图5所示,其中tf表示机器人腿部此时与地面没有接触,机身整体处于腾空相。在该步态下,可以通过调节触地角度和离地角度控制机器人执行转弯操作。

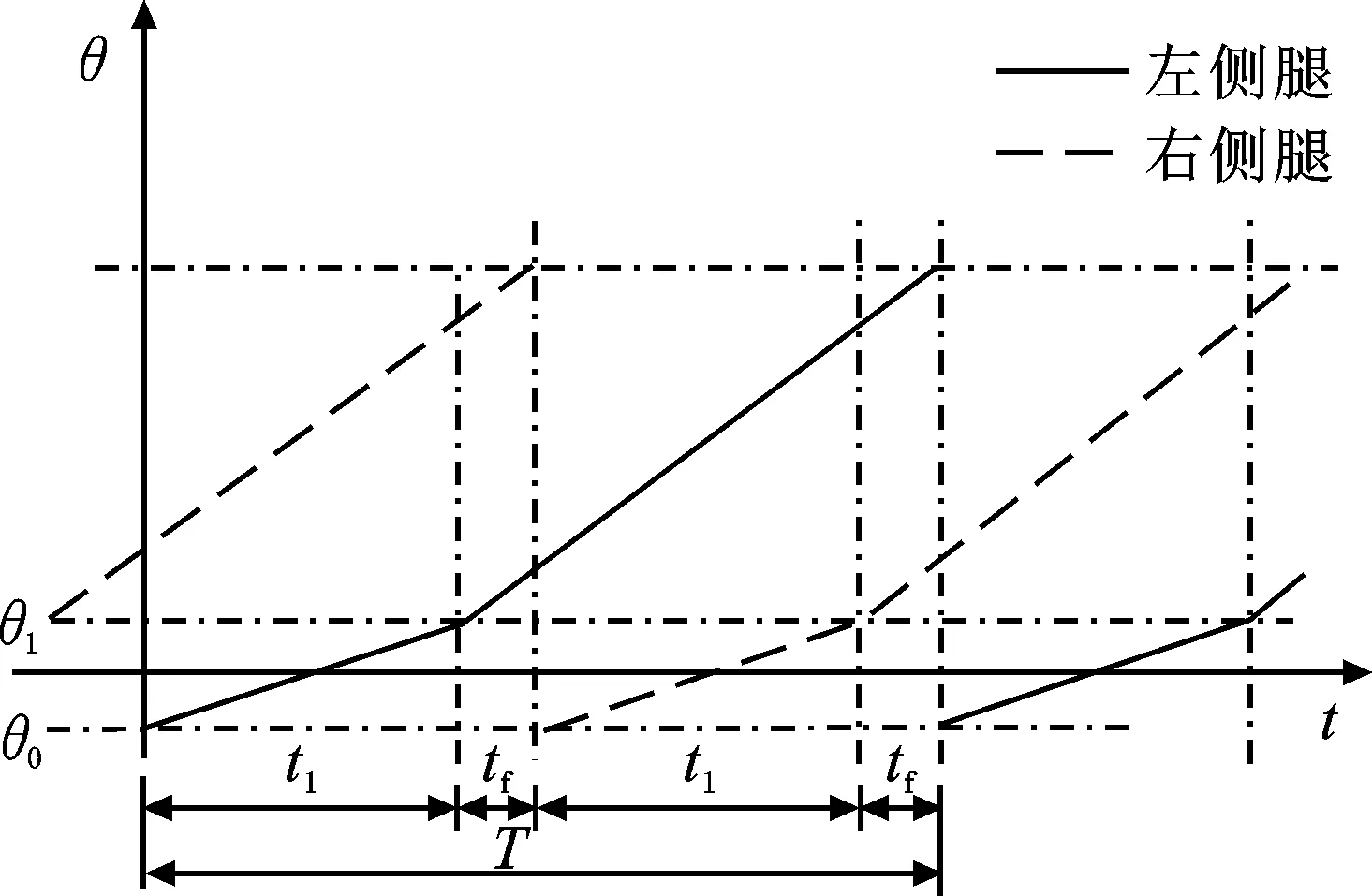
图5 三角步态控制参数

2.2 仿真分析

为证明具有柔顺性腿部的六足机器人具有更高的运动效能,固定触地角度、触地时长和离地角度等控制参数,研究扭簧刚度Kt为20 N·m/rad及1000 N·m/rad(刚性)时的运动速度变化及能量消耗水平。图6和图7给出了柔顺腿和刚性腿的结果对比,可以看出其他条件相同时,具有柔顺腿的机器人的运行速度更高,且等时间内消耗的能量更少。

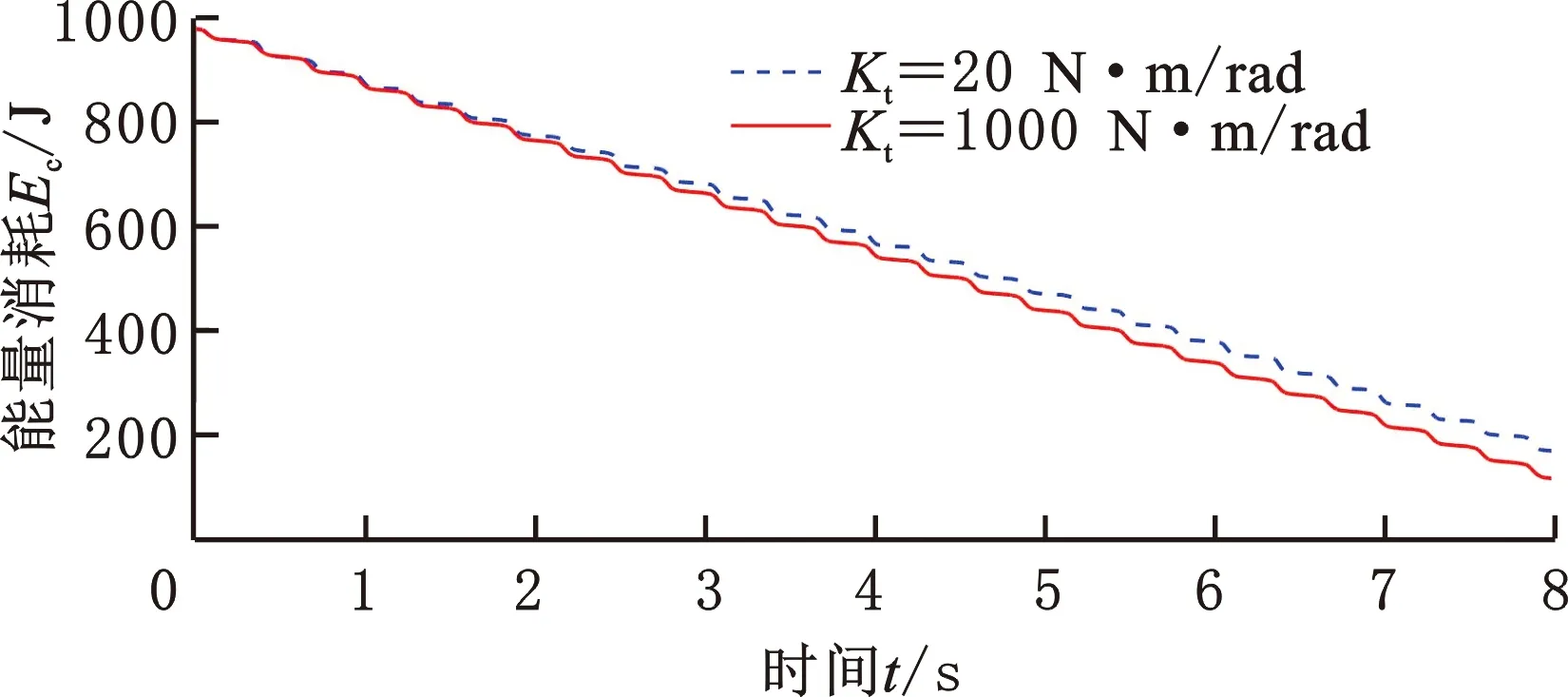
图6 柔顺腿和刚性腿机器人等时长内能量消耗

为探索腿部柔顺性对六足机器人运动的具体影响,本文在保持控制参数不变的情况下仅改变弧形腿的刚度大小,观察它对能量消耗速率和运动速度方面的影响。

图8给出了仅改变弧形腿扭簧特征刚度时机器人的能量耗散情况,可以看出当弧形腿的特征刚度从6 N·m/rad变化至25 N·m/rad(也即扭簧刚度逐渐增大)时,机器人能量耗散速度越来越快,并且当特征刚度从20 N·m/rad变化至25 N·m/rad时能量耗散速率的变化差距已经非常小,说明此时刚度的变化对系统的影响已经很小,图9所示的结果也展示了相同的影响。

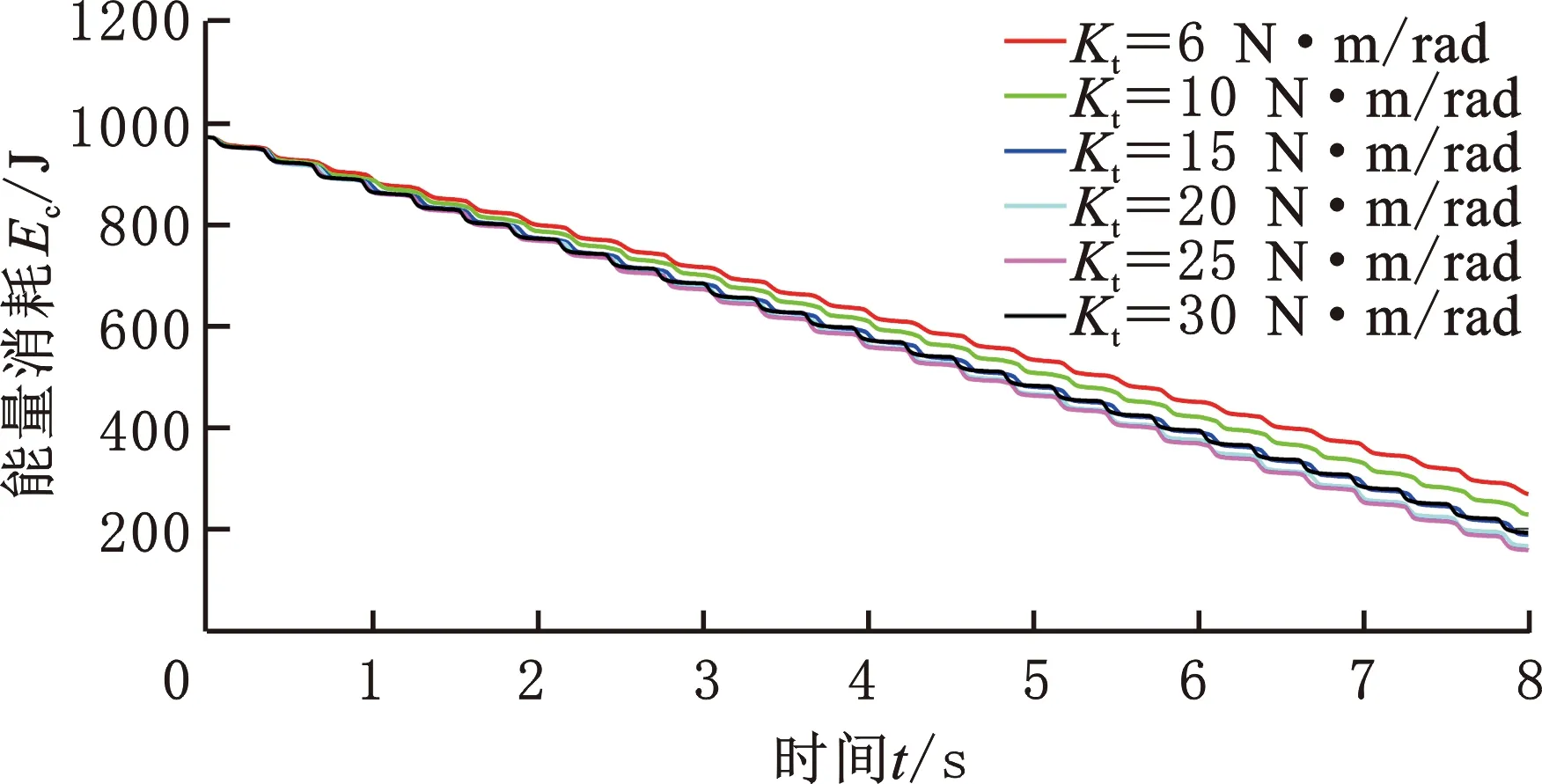
图8 具有不同刚度柔顺腿的机器人能量消耗情况

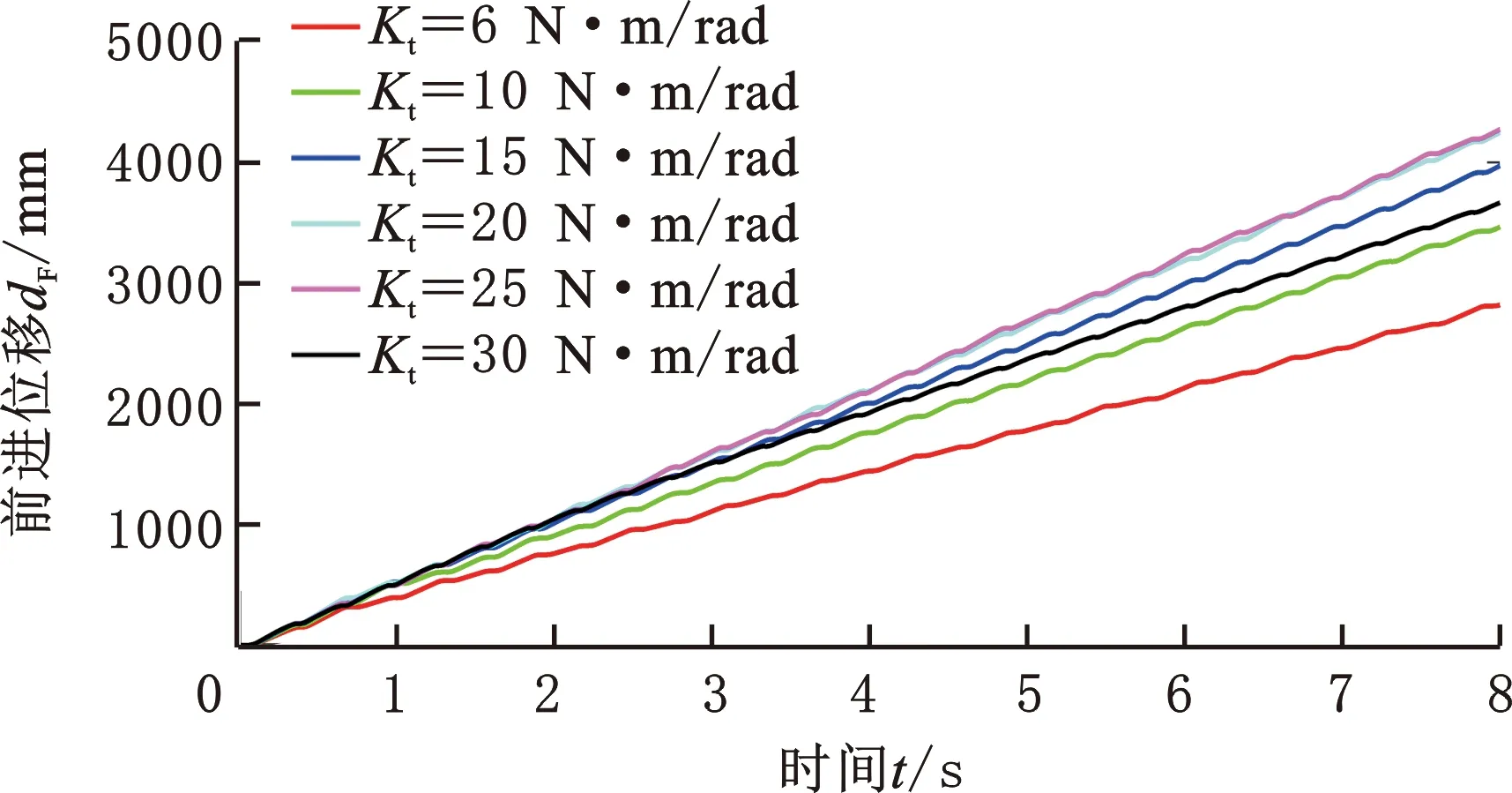
图9 具有不同刚度柔顺腿的机器人前进位移随时间变化

总体来说,越高的特征刚度意味着越快的速度,当刚度达到某个阈值且该值继续变化并不会对机器人的运行速度产生影响时,控制系统的其他参数(如触地角度、触地相扫掠角度以及步态周期等)成为了主要的影响参数。

3 实验研究

3.1 弧形腿刚度实验

为了验证使用伪刚体模型分析弧形腿变形的准确性,本文通过静态加载对弧形腿的刚度测量进行了研究,实验装置如图10所示。通过电子测力计施加载荷并控制输入载荷的大小,结果通过固定机位的相机记录。

图10 弧形腿刚度测量实验装置

测量结果和计算结果如图11所示,实验数据通过多次测量取均值,结果表明,使用伪刚体模型计算出的刚度与实验测得的刚度之间的误差很小,伪刚体模型可以准确地描述弧形腿的非线性变形行为,是一种有效的刚度建模方法。

图11 理论计算与实验数据对比

3.2 样机实验

仿生六足机器人样机如图12所示,它主要由弧形腿驱动模块、铝合金机架及电池、主控制器等硬件系统组成,尺寸参数见表2。

表2 六足机器人设计参数

图12 仿生六足机器人样机

实验方法为使用一组柔顺弧形腿和一组刚性弧形腿(其刚度远大于柔顺弧形腿的刚度)进行对比。分别测出两组弧形腿在相同控制参数下等时长内的能源消耗情况及平均前进速度变化,平均前进速度用等时长内的前进位移比较,将测得的数据进行对比分析,得到刚度对机器人运动性能的影响,所有的测试均在跳跃步态下进行,触地相扫掠角度为60°,触地时长约为100 ms,初始接触角度为60°,图13所示为跳跃步态下机器人在单周期内的运动过程。

图13 跳跃步态过程

在能源消耗测试时,使机器人在相同环境下(草坪)运行,每隔5 min测量机器人的剩余电量,结果如图14所示,其消耗规律与仿真结果一致,可以预见,当运行时间足够长时,与刚性腿机器人相比,具有柔顺腿的机器人能量消耗的平均速率总是更低。

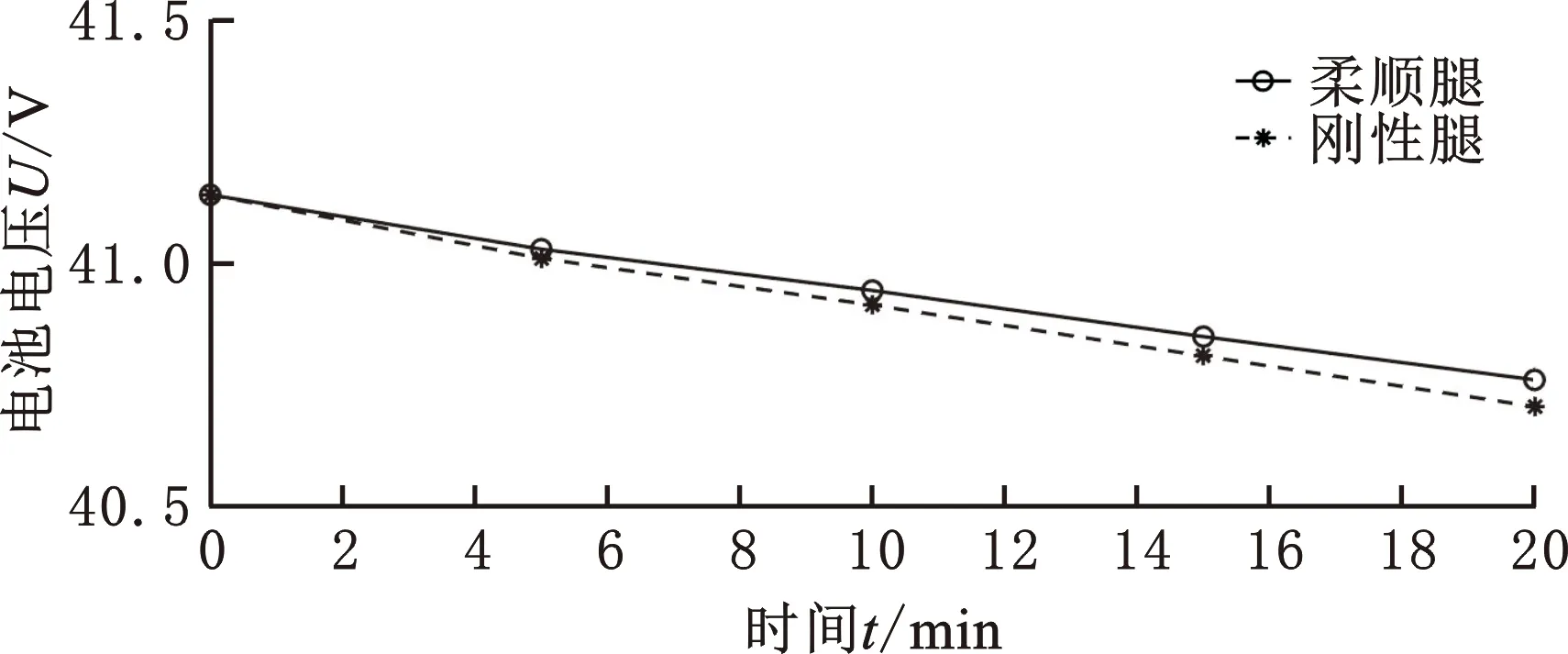
图14 能量消耗对比

在速度测量实验时,使机器人在相同的环境和控制参数下运行等长的距离,并测量其耗费时间,得到的实验结果与仿真结果非常吻合,具体实验结果见表3。在相同控制参数下,具有被动柔顺性的弧形腿机器人的单步跳跃距离可达200 mm,而刚性腿机器人的跳跃距离约为170 mm。由于柔顺腿机器人在飞行相耗费更长的时间,最终两者间的平均速度之比约为1.1。在同样运行4 m的距离后,刚性腿的耗费时间为13.8 s,柔顺腿的耗费时间为12.5 s。在相同设置条件下,具有柔顺腿的机器人的平均速度高于刚性腿机器人的平均速度。

表3 速度测量实验结果对比

能源消耗对比与速度测试的实验结果展示了与仿真研究类似的结果,即设置其他条件均相同时,与具有刚性腿的机器人相比,具有柔顺腿的机器人不仅可以达到更高的运行速度,而且能量利用效率也更高。

最后为了验证具有柔顺腿的六足机器人对不同环境的适应能力,本文开展了具有单侧地面突起的爬坡实验和复杂环境下的转弯测试。图15所示为具有柔顺腿的六足机器人分别在5°和10°的坡道上运行的过程,结果表明在两种坡道上机器人都能够稳定地运行。同样的设置下,刚性腿机器人在5°的坡度下可以稳定地运动,在10°的坡度下则在单侧地面突起处发生足底打滑、机身明显偏航等现象,导致机器人不能按照既定的指令往前运动。图16展示了在10°坡道遭遇单侧地面突起时装备两种腿的机器人的不同表现。在遭遇单侧地面突起后,刚度为1000 N·m/rad的刚性腿机器人的偏航角变化大于刚度为20 N·m/rad的柔顺腿机器人的偏航角变化,这表明刚性腿机器人受单侧地面突起的影响更大,偏航明显。柔顺腿的存在提高了机器人的运动稳定性,可以使机器人始终保持直线前进。

图15 爬坡测试

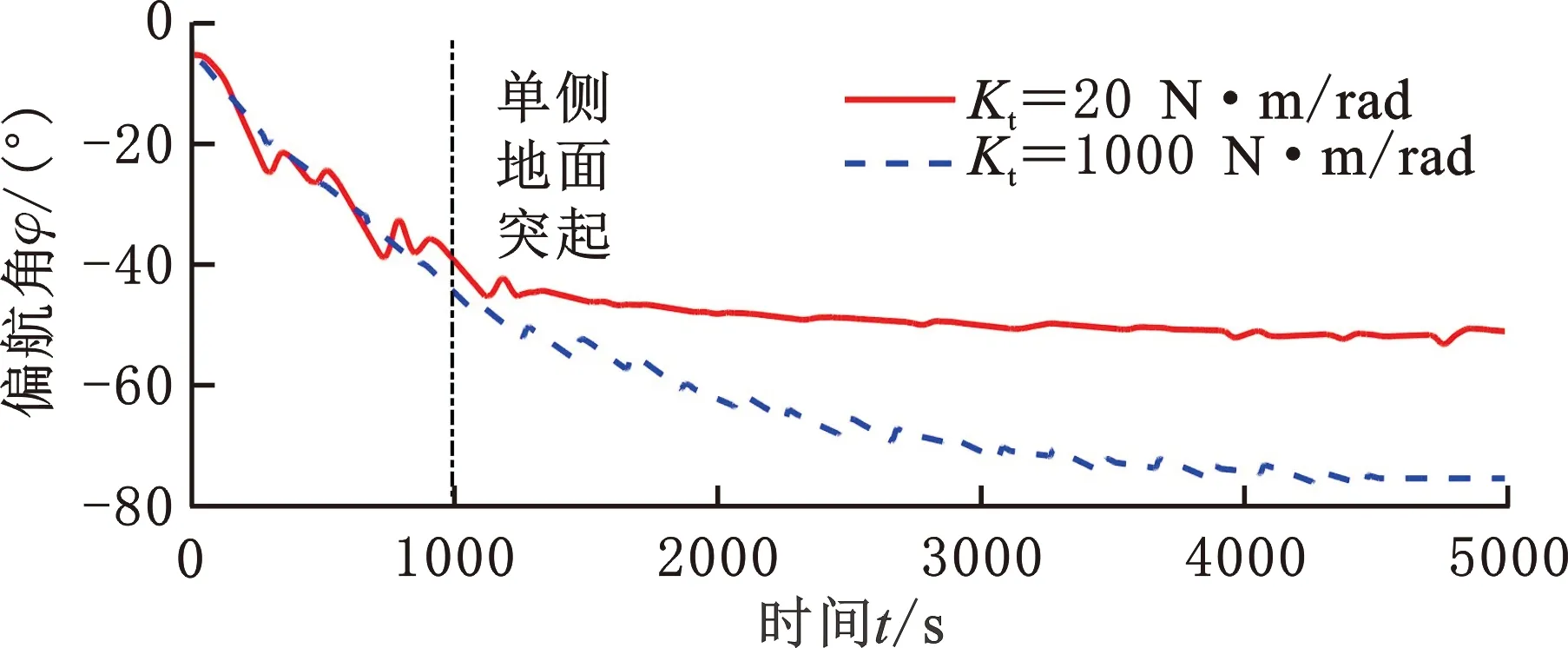
图16 10°爬坡测试时机器人偏航角变化结果

图17所示为具有柔顺腿的六足机器人在草地以及沙地上转弯时的轨迹跟踪状况,其中序号①、②分别表示较小和较大的转弯半径设置,两种转弯半径用障碍物的数量和图中红色轨迹线的弯曲程度表示。使机器人由正对障碍物出发,在靠近障碍物时执行转弯步态,转弯步态通过调节三角步态中的4个控制参数实现,在绕过障碍物后,使机器人恢复直线行走状态。从结果视频快照展示的结果中可以看出,六足机器人可以稳定地执行行走命令并绕过障碍物,由于坑洼的地形状态,刚性腿在此时可能会因落脚点不同而导致转弯失败,而弧形腿的被动柔顺特性使其能够自适应遇到的坑洼地形,因此它在复杂地形上的轨迹跟踪状态优于具有刚性腿的六足机器人。

(a)沙地转弯

4 结语

本文以探索柔顺腿对仿生六足机器人的具体影响展开研究,首先证明了使用伪刚体模型可以较为准确地建模出弧形腿在外力作用下的非线性变形行为,然后通过仿真和实验结果验证了具有柔顺弧形腿的仿生六足机器人在运行速度、能量消耗速率、环境适应性等方面均优于具有刚性腿的机器人。