RISC-V基础数学库性能优化

李 飞,郭绍忠,周 蓓,宋广辉,郝江伟,许瑾晨

(信息工程大学网络空间安全学院,河南 郑州 450001)

1 引言

纵观计算机发展史,从第1代电子管计算机(1946年～1957年)到第4代大规模、超大规模集成电路计算机(1970年至今),科学计算始终是各代计算机必备的重要功能。高性能基础数学库作为科学计算最基础的软件库之一[1],应用广泛,小到数字游戏、办公计算、教学分析等,大到海洋遥感、地质勘探、卫星轨道等精密计算科研领域。目前常见的基础数学库有GNU的glibc库[2]、Intel 的 MKL(Math Kernel Library)函数库[3]和AMD 的 libm 库[4]等。随着信息科学技术的发展,计算机体系架构逐渐变得多样化,不同的体系架构,底层的硬件设计、语言实现、存储机制也各有差异。为了保证基础数学库表现出较高的性能,开发人员都会研发一套契合自身架构的高性能基础数学库并基于处理器特性进行底层优化。

近年来,RISC-V 指令集架构ISA(Instruction Set Architecture)作为一种新兴的开源精简 ISA[5],因其可以免费使用和自由设计等特点,受到国内外厂商和研究人员的青睐。相较于x86架构和ARM架构,RISC-V提供了精简的基础指令集和扩展指令集,开发者可以基于这2种指令集以及自定义指令集扩展进行精细化的系统研发[6]。由于RISC-V的低功耗性、模块化设计和可扩展性等优势,开发人员在此领域取得了许多突破性科研成果,如瑞萨电子集团推出的基于64位RISC-V CPU内核的RZ/Five通用微处理器MPU(MicroProcessor Unit)[7]、中国科学院计算技术研究所的高性能 RISC-V 处理器核“香山”[8]和中国科学院上海微系统与信息技术研究所研发的宇航级高可靠嵌入式RISC-V卫星芯片等[9]。RISC-V作为计算机体系架构走向开放的必然产物,其软件系统和硬件系统应该都很完善,但目前开发者大都围绕RISC-V进行硬件开发,导致其软件生态很薄弱。2022年,首个RISC-V基础数学库开源发布(https://gitee.com/mathlib/RV-Libm),这一定程度上促进了RISC-V的软件生态发展。该数学库函数皆由RISC-V汇编语言实现,包含17个三角函数、6个双曲函数、4个指数函数等67个数学函数和2个内部调用函数。

通过对RISC-V基础数学库函数进行测试与分析发现,虽然其可以实现正确计算,但是函数中存在大量的访存指令及冗余指令。部分访存指令存在如下特征:在一段汇编程序内,如果有将寄存器的值写入栈空间的操作,在该段程序的结束位置,就会有将该寄存器的值从栈中取出的操作,即中间汇编程序段使用了该寄存器,而使用结束之后又还原了该寄存器值。将需要入栈和出栈的寄存器称为辅助寄存器。上述访存指令是为了保证RISC-V函数上下文寄存器依赖关系的正确性,在使用辅助寄存器之前和之后将其原来的值入栈和出栈,可以保存和恢复寄存器现场。通过这种方式实现寄存器的再利用,导致寄存器的利用率不高。而且,由于对内存进行读写比对寄存器进行读写速度上要慢很多,因此入栈和出栈指令的使用无疑会降低函数的性能。此外,RISC-V基础数学库函数中存在一定的冗余指令,尤其是在RISC-V函数的邻近空间内连续多次出现相同指令操作时,从局部的角度分析这些具有一定关联性的指令并进行重构,一定程度上可以提升RISC-V的函数性能。

针对上述问题,本文提出了面向RISC-V基础数学库的性能优化方法。为了提高优化效率,利用自动插桩技术预先检测出测试集对应的不同路径,以路径为单位进行有针对性的线性优化。基于检测到的路径,首先根据队列式寄存器分配策略将函数中对内存的读写优化为对寄存器的读写;然后对局部组合功能指令进行重构,尽可能多地删除冗余指令。实验结果表明,该方法可以对RISC-V数学函数进行有效的性能优化。

2 相关工作

传统的寄存器分配算法有Chaitin等[10]提出的图着色算法GCRA(Graph Coloring Register Allocation)和Poletto等[11]提出的线性扫描算法LSRA(Linear Scanning Register Allocation)。图着色寄存器分配算法是将寄存器分配问题抽象成图着色问题,通过构造干涉图对共同边的不同节点以不同颜色完成着色,直观地分析2个变量在节点处是否冲突,相互冲突的变量不能同时占用同一寄存器,以此对干涉图进行构造和化简,完成寄存器的分配。但是,当此算法运用到大基本块或者全局范围时,构成的干涉图可能过于复杂,增加了寄存器分配的复杂度。线性扫描算法是寄存器分配较快的算法,通过对待分配寄存器的一次性扫描以及将各个变量生命周期的结束时间进行排序,完成寄存器的分配。该算法虽然具有很快的效率,但是仅对待分配的寄存器以及生命周期结束的寄存器进行回收再分配,存在生命周期未结束且下文重新写入的寄存器和不同路径中无依赖关系的寄存器利用率低的问题。

2012年,郭正红等[12]提出层次结构寄存器分配策略,该策略通过判断是否有可分配的通用寄存器,SIMD寄存器高位和保存寄存器是否空闲来完成寄存器分配。此方法引入SIMD寄存器高位来缓解标量浮点寄存器分配的压力,但是SIMD寄存器高位和保存寄存器不直接参与分配过程,而是在使用之前和之后进行额外的处理。比如当使用SIMD寄存器高位完成64位浮点计算之后,就需要进行一次数据交换,将其移动到标量浮点寄存器,相比于直接分配通用寄存器,这些交换增加了额外的开销。而保存寄存器的使用,为了不改变其原本的值,需要将此寄存器的值存进栈空间,当分配使用之后,还需要将原来的值从栈中取出,以恢复寄存器依赖,这些访存指令的使用会影响函数的性能。

2013年,姜军等[13]提出了一种局部寄存器分配的优化策略,该策略是在进行全局寄存器分配之前,预估局部寄存器的需求,并根据每条指令的胖点值去分析该位置需要的寄存器个数,在不提高局部寄存器分配复杂度的同时,保证了局部空间内尽可能多地分配到寄存器。此方法需要提前预估需要的局部寄存器个数,并在全局开始时进行预留。但是,在进行寄存器分配时,如果分配的无依赖寄存器个数处于紧张状态,那么在RISC-V函数优化中很难实现在全局范围内寄存器的预留。此外,该方法需要对每一条指令进行胖点值赋值和判断,这会产生不必要的访存指令,增加了代码执行的开销。并且,该方法主要适用于国产CPU SW1600专用编译器,因此对于RISC-V数学函数的汇编程序优化具有一定的局限性。

3 性能优化方法

RISC-V基础数学库包含67个数学函数和2个内部调用函数,尽管在实现时已最大限度地精简RISC-V函数代码,但是仍存在寄存器利用率不高、访存指令过多及存在冗余指令等问题。由于各函数的特性及指令构成不同,具体的优化部分也不尽相同。但总体来说,性能优化方法可以分为3个步骤:函数路径的自动检测、队列式寄存器分配及冗余指令重构,如图1所示。

3.1 函数路径的自动检测

RISC-V数学函数的汇编代码量大,分支判断复杂,直接进行优化具有一定的难度。RISC-V函数的分支虽多,但是根据函数的“归约-逼近-重建”实现算法及数学性质,可以将不同输入归约到同一区间内。例如,exp(a+b)=exp(a)+exp(b)和cos(a+2π)=cos(a),可以将输入值归约到临近零点的区间内,结合查表完成近似计算。当输入为函数的异常值时,例如无穷数、弱规范数等,RISC-V数学函数无法进行计算,则会进入异常处理机制,进而引发异常中断。将不同输入进行归约之后,定义域内不同区间的输入所经过的路径大概率是一致的。根据浮点数分布规律,生成可以覆盖函数定义域内不同区间的测试集。基于该测试集检测其所经过的路径、可得到关键路径、次要路径和其他路径。由局部到整体地依次对检测到的路径进行优化,可以使优化工作更加准确高效。以路径为单位进行线性优化的优势是一条路径内汇编指令的改变不会影响其他路径的正确计算,而且有助于定位优化后引起精度变化的指令位置。关键路径自动检测方法通过对函数各分支进行编码,并将编码加载进浮点寄存器设计成路径探针,自动插桩到函数各分支的首行,不同的测试样本经过路径探针时,会基于上一个路径探针中浮点寄存器存储的编码计算两者的和,最后对路径探针和进行解码,可得各测试样本所经过的路径,其整体流程如图2所示。

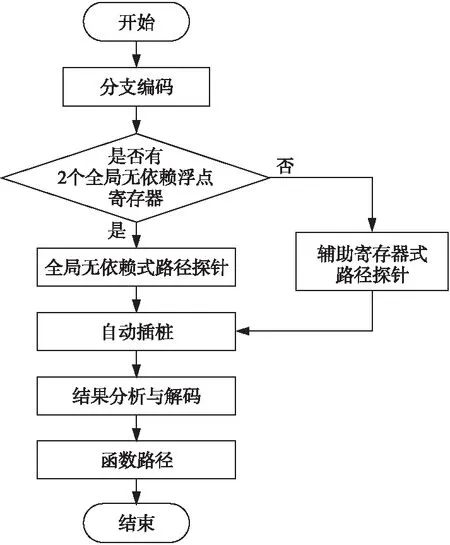
Figure 2 Automatically detection process of function path

3.1.1 分支编码与路径探针设计

所谓分支编码,就是对RISC-V函数的n个分支以十进制序号从1至n进行顺序编码,并将首位为1末尾为n-1个0的二进制字符串与十进制序号进行配对,以这种方式组成二进制字符串,解码得到的结果具有唯一性。由于RISC-V寄存器通常支持12位的立即数读写,所以将二进制字符串转化为十六进制,以支持更大范围的序号写进浮点寄存器,如表1所示。

Table 1 Branching code table

路径探针的作用是以编码累加的方式记录测试样本所跳转的分支。从起始分支到返回分支,中间涉及的分支顺序构成了测试样本在函数中经过的路径。为了准确记录测试样本跳转的分支顺序,需要将路径探针插入到每一个分支首行。因为路径探针插入后测试样本的路径易发生改变,所以必须选择不影响函数原来寄存器依赖关系的寄存器,并结合表1中十六进制编码对路径探针进行设计,分为以下2种情况:

(1)当函数有2个以上未使用过的浮点寄存器时,此时这2个浮点寄存器全局无依赖,依此构造全局无依赖式路径探针GDPP(Global Dependency- free Path Probe)。假设函数中含有2个全局无依赖寄存器ft1和ft2,则GDPP-x的实现如图3所示。

Figure 3 Global dependency-free path probe

指令说明:li为加载立即数指令;fmv.d.x为整数向双精度浮点传送指令;fadd.d为双精度浮点加指令。GDPP-1插入的位置为函数的第1个分支,GDPP-2对应第2个分支。若测试样本经过GDPP-1和GDPP-2,则GDPP-2中的第11行目的寄存器ft1的值为2个探针的编码和。

(2)若函数内没有2个以上全局无依赖寄存器,则需要借用其他寄存器设计辅助寄存器式路径探针ARPP(Auxiliary Register Path Probe)。为了不改变探针上下文寄存器的依赖关系,需要在使用辅助寄存器之前和之后将其值入栈和出栈,以保存和恢复寄存器现场。经探针将编码计算之后,将计算的编码结果入栈,以便下一个探针从该栈中取出继续计算,ARPP-x的实现如图4所示。

Figure 4 Auxiliary register path probe

指令说明:fld为双精度浮点加载指令,fsd为双精度浮点保存指令。图4中,ARPP-2的第10、11行是在使用辅助寄存器fa1和fa2之前将其值先存入栈中保存现场;第12行是将上一个探针的结果从栈中取出,让当前探针使用;第16行是将当前探针计算得到的结果入栈,以便下一个探针使用;第17、18行为恢复辅助寄存器fa1和fa2的寄存器现场。

此外,由于部分函数中存在循环分支,且循环跳点一般不会在分支的首行,当测试样本经过循环分支时,对于同一探针结果就有多种不同路径的可能。如图 5所示,将数学函数内出现逆向跳转的情况定义为循环,即在当前分支内发生了向前面分支跳转的情况。假设L$2为循环分支,如果最终路径探针的值为110,则经过的分支有2种情况:一种是L$0→L$1→L$2→L$3;另外一种是L$0→L$1→L$2→L$0→L$1→L$2。

对于上述情况,显然在循环分支内仅在首行插入路径探针无法正确检测路径。因此,需要在循环区域内的分支中插入循环探针。循环探针可以是全局无依赖式路径探针,也可以是辅助寄存器式路径探针。由于循环探针的作用是为了记录在跳点处的循环次数,因此规定循环探针不能重复使用。所谓的循环区域内分支,即如图5中的L$0、L$1和L$2。最终循环次数等于循环探针的值减1,之所以减1是因为程序顺序执行时循环探针的值即为1。例如,如果L$1和L$2分支的循环探针值分别为2,则说明循环执行了1次;如果L$1分支的循环探针值为2,而L$2分支的循环探针为1,则说明循环在L$1分支内结束,以此得到循环次数,进一步得到是循环路径还是顺序执行路径。

Figure 5 Loop branch jump

3.1.2 自动插桩与解码

RISC-V数学函数的分支跳转复杂,无法直接判断输入所经过的路径,且测试集规模庞大,如果通过查看控制跳转寄存器的值去分析所有测试样本经过的路径,人工方式几乎难以完成。为了准确快速地得到测试集所涉及的RISC-V函数中的所有路径,本文实现了一个自动检测方法。首先,将3.1.1节设计的路径探针自动插桩到各分支的首行,在返回分支中将其对应路径探针的累加和存入RISC-V浮点输出寄存器fa0中。然后,通过调用待优化函数对测试样本进行自动测试,并将浮点寄存器fa0的结果输出到文件,此时文件中的结果为表1中分支对应的十六进制编码和。最后,对结果进行解码,即可得测试样本所经过的路径,其中经过的测试样本数最多的路径为关键路径。

路径探针的自动插桩实现过程为:获取RISC-V数学函数汇编程序每行的第1个连续字符串,若识别到的字符串非RISC-V指令集架构的汇编助记符,说明该字符为分支名称,则在该字符下插入路径探针。代码实现如算法1所示。

算法1路径探针自动插入

输入：每行第1个连续字符串。

输出：插桩后RISC-V数学函数程序。

1.for(i=0;i≤line;i++) {

2.get_str(S);

3.if(get_str(S)==‘’‖get_str(S)==‘ ’ ) {

4. continue;}

5.else{

6.while(strcmp(get_str(S),RV_mn)!=0) {

7.mv_down(i+P_l(GDPP-xor ARPP-x));

8.inster(GDPP-xor ARPP-x,i);

9. }

10. }

11.}

算法1中,第6行判断非空字符串是否为RISC-V助记符,第7行表示将函数汇编程序从i行开始下移一个探针大小行,第8行将GDPP-x或者ARPP-x插入到汇编程序的第i行。

根据3.1.1节表1中各分支对应的二进制编码方式,可以发现不同分支的二进制和具有唯一性。通过将结果文件中路径探针的十六进制编码和转化为二进制,再将二进制中的1进行顺序转置,则转置后1的位置序号即为分支的十进制编码,由此可得测试样本所经过的路径。

3.2 队列式寄存器分配策略

根据RISC-V基础数学库函数的实现特性,函数中有较多以指令组合的方式完成计算功能的程序段。为了使组合方法具有通用性,函数源码中利用了辅助寄存器以固定格式进行组合,因此辅助寄存器会被写入新的变量值,这就导致辅助寄存器原来的值被覆盖,进而造成下文寄存器的依赖错误。因此,在函数源码中使用辅助寄存器之前需要将原来的值存入栈空间,待组合功能完成之后,再从栈中取出,以这样的方式去保存和恢复辅助寄存器对下文的依赖。如图6所示,以Code#1中RISC-V的lg函数中部分程序段为例,对该程序段分析可知,实际完成的功能是复制ft0浮点寄存器的〈63:52〉位的值和fa0浮点寄存器〈51:0〉位的值,组合成一个新的双精度浮点数存入目的寄存器fs1中。然而,RISC-V中没有直接实现此功能的汇编指令,因此只能以Code#1中组合的方式实现。根据RISC-V指令集特性及指令组合方法,需要借助整数寄存器s8、s9、s10、s11完成Code#1中的功能。Code#1中复制ft0的〈63:52〉位是通过将ft0寄存器的值移动到整数寄存器s8(第5行),然后将由〈63:52〉位全为1和〈51:0〉位全为0格式的十六进制数加载进整数寄存器s9(第6行),s8和s9经过逻辑与操作形成新的值存入s8(第7行)。fa0寄存器〈51:0〉位的复制以同样的方式进行操作并存入s9整数寄存器(第8～10行)。最后s8和s9进行逻辑或操作得到最终值,并将其存入浮点寄存器fs1(第11、12行)。

Figure 6 Combination implementation of copy instruction

从图6 Code#1的第8～11行发现,整数寄存器s10、s11、s9、s8的值进行了额外的更新,这是为了不改变下文寄存器对这些寄存器的依赖,在使用这些寄存器之前和之后,需要保存和恢复寄存器现场,即第1～4行和第13、14行。这些访存指令无疑会影响函数的性能,如果使用不影响下文依赖的寄存器代替s8～s11寄存器,则就不需要入栈和出栈,函数性能也会有一定的提升。

队列式寄存器分配策略就是在RISC-V函数路径中,根据待优化位置和寄存器的依赖复杂度构成3种不同优先级的寄存器队列。3种寄存器队列都是由可以代替辅助寄存器而不改变原依赖关系的寄存器构成,因此队列式寄存器的分配不需要入栈和出栈,从而减少访存指令数,寄存器分配优先级依次为第1队列、第2队列和第3队列。

第1队列为全局无依赖寄存器,此类寄存器是RISC-V数学函数从未使用的寄存器,也可以是其他路径与优化路径无交集分支内的寄存器。对这类寄存器进行再分配不会影响任何路径的寄存器依赖,并且适用于程序中任一位置优化,但是这类寄存器一般数量较少。当第1队列寄存器数量不能满足需求时,则需要借助第2队列寄存器完成分配。第2队列寄存器为下文先被更新的寄存器,当在优化位置的下文有寄存器A作为目的寄存器出现时,将其分配至优化位置代替辅助寄存器,不会对依赖寄存器A的下文程序产生影响。此队列更适合路径的前部分程序优化,因为对前部分进行优化时,后部分寄存器可以作为目的寄存器的数量更多。第3队列寄存器为程序周期已结束的寄存器,如果寄存器A在程序中是最后一次出现,则代表该寄存器的程序周期已结束。当对程序周期已结束寄存器的下文程序进行优化时,则可以对寄存器A进行再分配,将其用作优化所需的寄存器,同样不会影响函数的正确计算。第3队列寄存器更适合路径的后部分程序优化,因为此时前部分程序周期已结束的寄存器数量更多。第2队列和第3队列根据不同优化位置以不同的规则对寄存器进行判断,所以这2个队列的寄存器是动态变化的。以图6 Code#1为例,根据队列式寄存器分配策略找到4个寄存器代替辅助寄存器s8～s11,优化流程如图7所示。

Figure 7 Optimization process of queue register allocation strategy

图7中子图1为lg函数中的代码段,为了减少访存指令数,首先在此位置全局搜索符合第1队列全局无依赖的寄存器,仅有寄存器a2。以a2寄存器代替子图1中的辅助寄存器s8,得到子图2。经过子图6发现,子图2中仍有辅助寄存器存在,此时第1队列已经无寄存器可分配,根据队列式寄存器分配策略需要搜索符合第2队列的寄存器。由子图7发现,第137行和第138行有寄存器a3和a4可以作为目的寄存器,则可以将子图2中的辅助寄存器s9和s10替换为a3和a4,得到子图3,且不影响第138行之后其他寄存器对a3和a4的依赖。经过子图8判断,子图3中仍有辅助寄存器s11未被替换,若继续向下搜索符合第2队列的寄存器,会增加搜索复杂度,更好的方法是向上搜索符合第3队列的寄存器。根据子图9显示,该代码段的上文第112行有寄存器a7的程序周期已结束,则以a7代替s11得到子图4。通过再判断发现,该程序段已没有辅助寄存器,即可以删除Code#1中第1～4行和第13～16行的访存指令,完成寄存器分配。

Figure 8 Analysis of program segment function

Figure 9 Analysis of redundant instruction

3.3 冗余指令重构

RISC-V基础数学库中函数数量多、代码量大、算法实现复杂,如果逐个分析所有函数的所有单指令操作,不仅需要很大的时间成本和人工成本,并且还容易忽略指令之间的关联性。根据RISC-V组合指令的特性,一段组合指令完成的功能是确定的。如果从局部的角度分析程序段实现的功能,就可以将单指令正确性扩大为程序段正确性,即只要保证在一定的局部空间内对程序段进行重构,不改变下文程序的依赖,则RISC-V数学函数的功能依然保持正确。以RISC-V读取浮点控制寄存器的值并存入双精度浮点寄存器和双精度浮点先取负再乘加功能为例进行详细介绍,如图8所示。第1～4行完成的功能是读取浮点控制寄存器的值并存入浮点寄存器ft4中。由于RISC-V中没有直接实现该功能的指令,因此先通过frcsr指令将浮点控制寄存器的值读入整数寄存器s8,再使用fmv.d.x指令将整数寄存器的值移动到浮点寄存器,其中整数寄存器s8为辅助寄存器。第5～7行实现的是双精度浮点先取负再乘加,然而RISC-V中仅有双精度浮点乘加指令fmadd.d,因此在计算乘加之前,需要先利用fneg.d指令将相乘寄存器中的一个寄存器值取负,待乘加计算结束之后,再还原该寄存器值。

在RISC-V函数中需要重复完成此类功能时,在函数程序中仍然会以相同的方式组合为RISC-V程序段,因此导致产生冗余指令。图9为RISC-V函数fmod中重复实现上述功能的相邻程序段,根据图8该类功能的组合实现,图9第773～776行和第798～800行分别对应图8中第1～4行和第5～7行实现的功能。

图9中,第775和779行fmv.d.x指令是将整数寄存器s8的值移动至浮点寄存器ft4和ft5,在这2个指令之间的ld、sd、frcsr指令的功能是将原来s8的值出栈、入栈、读浮点控制寄存器的值放入s8。由于这2行之间浮点控制寄存器的值没有发生改变,因此第774行寄存器s8的值可以运用到第779行。从局部角度分析,第778行再次读取浮点控制寄存器的值并将其写入寄存器s8为多余操作,第776和777行出栈结束后再入栈也毫无意义,因此第776,777,778行为冗余指令,可以优化为图10中子图1的第773～777行。同样的原理分析#RISC-V_fmod中的第800和801行,连续地使用fneg.d指令将浮点寄存器fs10的值还原之后再取负,那么其依然为第798行fs10的值,因此这2行为冗余指令,经优化可得到图10中子图1的第798～801行。

Figure 10 Redundant instruction optimization

根据3.2节队列式寄存器分配策略,RISC-V的fmod函数程序的此位置有符合第3队列的整数寄存器a5可以进行再分配,代替图10中子图1整数寄存器s8。此外,也有符合第1队列的浮点寄存器ft3,可以将子图1中第798行浮点寄存器fs10的值取负之后存入ft3浮点寄存器,从而取消第801行浮点寄存器fs10的值还原操作,最终将图9代码段优化为图10子图2代码段。

4 实验及结果分析

为了验证本文方法的有效性,使用遵循RVV-0.10规范的指令功能模拟器Spike[14]及RISC-V的gcc工具链[15]进行各项测试。测试项分别为:精度测试、函数路径自动检测方法测试、队列式寄存器分配和冗余指令优化方法的效果对比测试及所有RISC-V函数优化前后的性能变化测试。

4.1 精度测试

为了测试优化后的函数精度是否发生变化,在优化之前和之后分别对RISC-V基础数学库函数进行了精度测试。测试集由随机生成的函数定义域内的5×1010个双精度浮点数据构成。精度测试是通过与高精度MPFR[16]数学库函数计算相对误差(relativeULP)实现,计算过程如式(1)所示:

relativeULP=

(1)

在相同测试样本下,Expression(x)RISC-V代表RISC-V数学函数计算得到的结果,Expression(x)mpfr代表此函数在MPFR上计算得到的结果,ulp(x)mpfr代表MPFR函数计算得到结果的ULP(Unit in the Last Place)值。经测试,67个数学函数中有58个函数相对误差处于(0,1] ULP,9个函数处于[1,2] ULP,其中最大相对误差1.90 ULP是由反误差函数erfc产生的。测试结果表明,优化之后RISC-V基础数学库函数精度与优化之前的保持一致。

4.2 函数路径自动检测方法测试

RISC-V基础数学库函数类型多样,本文基于此方法对cotd、fma、cos、erf、exp、pow、lgamma、log2、erfc、lround共10个典型函数进行测试,检测其不同路径及样本通过率。由于不同函数检测到的路径数量不同,所以本文测试以各函数的关键路径为例进行统计与分析。

为了保证测试的有效性,本文按照 IEEE-754 浮点数分布的全浮点域指数分布测试集的生成方法[17],在函数定义域内生成 5×106个双精度浮点测试样本,最大限度地保证覆盖函数的所有路径,以确保基于关键路径优化时不影响其他路径的正确计算,结果如表2所示。

Table 2 Results of critical paths automatic detection

经测试,此方法可以快速得到所有测试样本的准确路径。个别函数的测试样本绝大部分会经过同一路径完成计算。例如,cotd函数的_rv_cotd→ .L2→.L6路径样本通过率为96.10%;lb函数的_rv_lb→L$3路径样本通过率为99.95%。而大部分函数的关键路径样本通过率大约占总测试集的一半。例如,erf、exp、lgamma和lround函数在关键路径的样本通过率分别为49.87%,49.53%,49.88%和52.46%。由于函数程序由各分支代码段组成,不同分支之间的跳转构成了不同路径,因此,样本通过率占比较高的路径复杂度对函数性能表现会起到主要作用,依次通过检测到的路径对函数进行性能优化,不仅降低了程序分析的难度而且提高了优化效率。

4.3 2种优化方法的性能测试

本文3.2节和3.3节分别对影响函数性能的不同部分以不同的方法进行了优化。为分析两者的优化效果,以不同类型的典型函数sin、acos、cbrt、scalb、fmod、pow、lgamma、lb、erfc、ldexp为例,分别对以队列式寄存器分配优化后的函数以及进行冗余指令优化后的函数进行性能测试与分析。

性能测试通过获取随机生成函数定义域内的1 000个测试样本的平均时钟周期实现。为了确保得到的平均时钟周期的准确性,首先对函数进行预热,以此减低外部环境对测试产生的影响。预热代码如下:

for(inti=0;i

arry[i]=(float)rand() / ((float)RAND_MAX+1)*((1)-(0))+(0);}

for(inti=0;i<10;i++){//sin函数预热

_rv_sin(arry[i]);}

各函数的平均时钟周期通过式(2)计算:

(2)

其中,cycleij表示样本xj第i次测试得到的时钟周期数,m表示每个测试样本的测试次数,n表示测试样本的个数。在本文中m取10,n取1 000,性能测试结果如图11所示。

Figure 11 Performance changes of two optimization methods

关于2种优化方法需要说明的是,队列式寄存器分配方法和冗余指令优化是依次递进对函数进行优化,即在使用队列式寄存器分配方法对函数进行优化之后,再对函数进行冗余指令重构。从图11的测试结果可知,队列式寄存器分配方法和冗余指令优化对函数的性能有不同程度的提升。其中,队列式寄存器分配方法普遍对函数性能提升显著,如acosh、cbrt、lgamma函数性能由223,225,537个时钟周期提升至176,151,295个时钟周期,提升比分别为21.08%,32.89%,45.07%。这是由于在此类函数中存在较多的入栈和出栈操作,因此经该方法优化后得到了较高的性能提升。冗余指令优化根据函数自身指令冗余程度的不同有不同的性能提升,即指令冗余程度较高的函数经该方法优化后性能提升更明显。例如,lgamma函数性能由295个时钟周期提升至206个时钟周期,提升比为30.17%。而冗余指令程度较低的函数性能提升不明显,如lb函数仅提升1个时钟周期。

4.4 RISC-V基础数学库性能测试

RISC-V基础数学库共有69个函数,其中有2个为内部调用函数。为分析RISC-V基础数学库的整体性能变化,本节使用4.3节测试方法对优化前后的67个RISC-V函数进行性能测试(addtc 函数和cvttqc 函数属于内部调用函数,不进行性能测试)。由于Spike是功能模拟器,测试的时钟周期数和实际时钟周期数会有微小差异,但是优化前后的函数性能测试都是基于Spike进行的,即在环境变量保持一致性的条件下,计算性能提升比具有更准确的参考价值,并使用式(3)所示的方式计算整体性能平均提升比:

(3)

其中,AOPIR为整体性能平均提升比,f为函数的总个数,Si为第i个函数优化前的时钟周期,Oi为第i个函数优化后的时钟周期。性能测试结果如图12所示,逻辑实现较复杂的函数性能提升更明显,如tand、sincos、scalb、cotd、acos等函数,性能分别由232,437,134,229和109个时钟周期优化为116,254,75,113和55个时钟周期,性能提升比分别为50.00%,41.88%,44.03%,50.66%和49.54%;实现较简单的函数性能提升较少,如atan、trunc、frexp、modf等函数,性能分别由51,47,38和50个时钟周期优化为45,41,37和42个时钟周期,性能提升分别为11.76%,12.77%,2.63%和16.00%;而对于逻辑简单的数值处理函数,其本身没有优化空间,此类函数性能没有提升,如unordered、nearbyint、fp_class、fabs等函数。

Figure 12 Performance of RISC-V basic math library before and after optimization

为进一步分析本文优化方法对函数的性能提升与指令的关系,分别对优化前后函数中的访存指令数和总指令数进行统计,并给出各函数的性能提升比,其结果如表3所示。优化之后函数的访存指令数以及总指令数相较优化前的都有不同程度的减少。根据表3各函数的性能提升比结果发现,性能提升比与访存指令减少数总体呈正相关。然而部分函数相较于其他函数虽然访存指令减少得更多,但是性能提升却小于其他函数的。如cotd函数的访存指令数由1 943优化为1 742,共优化掉201条访存指令,性能提升比为50.66%;然而erf函数访存指令数由332优化为85,共减少247条访存指令,性能提升比为41.75%。在erf函数的访存指令减少数多于cotd函数的情况下,其性能提升比却小于cotd函数的,这是由于erf函数的访存指令减少数并没有集中在关键路径中,而随机生成的测试集主要通过关键路径,因此获取的时钟周期数会大于访存指令集中在关键路径中的函数的时钟周期数,即性能提升比会小于此类函数的。

Table 3 Number of instructions before and after RISC-V basic math library optimization

5 结束语

本文根据RISC-V基础数学库函数的汇编程序实现特性,提出了性能优化方法。该方法主要分为函数路径自动检测、队列式寄存器分配以及冗余指令重构。实验结果表明,在精度保持不变的情况下,基于上述方法,67个RISC-V数学函数由平均144个时钟周期优化为85个时钟周期,性能平均提升了29.61%,验证了性能优化方法的有效性。依据科学的测试方法对函数完成测试,并对结果做了较详细的分析,得到的数据具有一定的参考价值。目前优化后的高性能RISC-V基础数学库源码已开源发布在https://gitee.com/mathlib/RV-Libm。当前工作主要在功能模拟环境中进行,待RISC-V相关条件具备的时候,可以将其部署在硬件环境下。